沪科版（2024）九年级上册21.1 二次函数同步测试题

这是一份沪科版（2024）九年级上册21.1 二次函数同步测试题，共86页。


TOC \ "1-3" \h \u
\l "_Tc17744" 【题型1 几何图形中线段最值问题】 PAGEREF _Tc17744 \h 1
\l "_Tc1983" 【题型2 两线段和的最值问题】 PAGEREF _Tc1983 \h 2
\l "_Tc25836" 【题型3 周长的最值问题】 PAGEREF _Tc25836 \h 4
\l "_Tc31085" 【题型4 面积的最值问题】 PAGEREF _Tc31085 \h 6
\l "_Tc11133" 【题型5 线段和差倍分的最值】 PAGEREF _Tc11133 \h 8
\l "_Tc11136" 【题型6 由二次函数性质求二次函数的最值】 PAGEREF _Tc11136 \h 9
\l "_Tc31248" 【题型7 由二次函数的最值求字母的值】 PAGEREF _Tc31248 \h 10
\l "_Tc12038" 【题型8 由二次函数的最值求字母的取值范围】 PAGEREF _Tc12038 \h 12
【题型1 几何图形中线段最值问题】
【例1】（23-24九年级·广西钦州·期中）如图，线段AB=10，点P在线段AB上，在AB的同侧分别以AP,BP为边长作正方形APCD和BPEF，点M，N分别是EF，CD的中点，则MN的最小值是（ ）
A．2B．3C．5D．6
【变式1-1】（23-24九年级·安徽合肥·阶段练习）如图，AB=6，点C是AB上的动点，以AC、BC为边在AB同侧作等边三角形，M、N分别是CD、BE中点，MN最小值=（ ）
A．3B．32C．322D．332
【变式1-2】（23-24九年级·广东江门·阶段练习）如图，在矩形ABCD中，AB=3，BC=4，将对角线AC绕对角线交点O旋转，分别交边AD、BC于点E、F，点P是边DC上的一个动点，且保持DP=AE，连接PE、PF，设AE=x0(1)填空：PC= ，FC= ；（用含x的代数式表示）
(2)若△PEF的面积为S，求S与x的函数关系及△PEF面积的最小值；
(3)在运动过程中，PE⊥PF是否成立？若成立，求出x的值；若不成立，请说明理由．
【变式1-3】（23-24九年级·广东广州·期中）如图，在正方形ABCD中，AB=7，F是边CD上的动点，将△ADF绕点A顺时针旋转90°至△ABE，将△ADF沿AF翻折至△AGF，连接EF、BD交于点H，连接GH，则△EGH面积的最大值为 ．
【题型2 两线段和的最值问题】
【例2】（（23-24·安徽合肥·一模）如图，直线y=−x＋3与x轴、y轴分别交于B、C两点，抛物线y=−x2+bx+c经过点B、C，与x轴另一交点为A，顶点为D．
(1)求抛物线的解析式；
(2)在x轴上找一点E，使EC+ED的值最小，求EC+ED的最小值；
(3)在抛物线的对称轴上是否存在一点P，使得∠APB=∠OCB？若存在，求出P点坐标，若不存在，请说明理由．
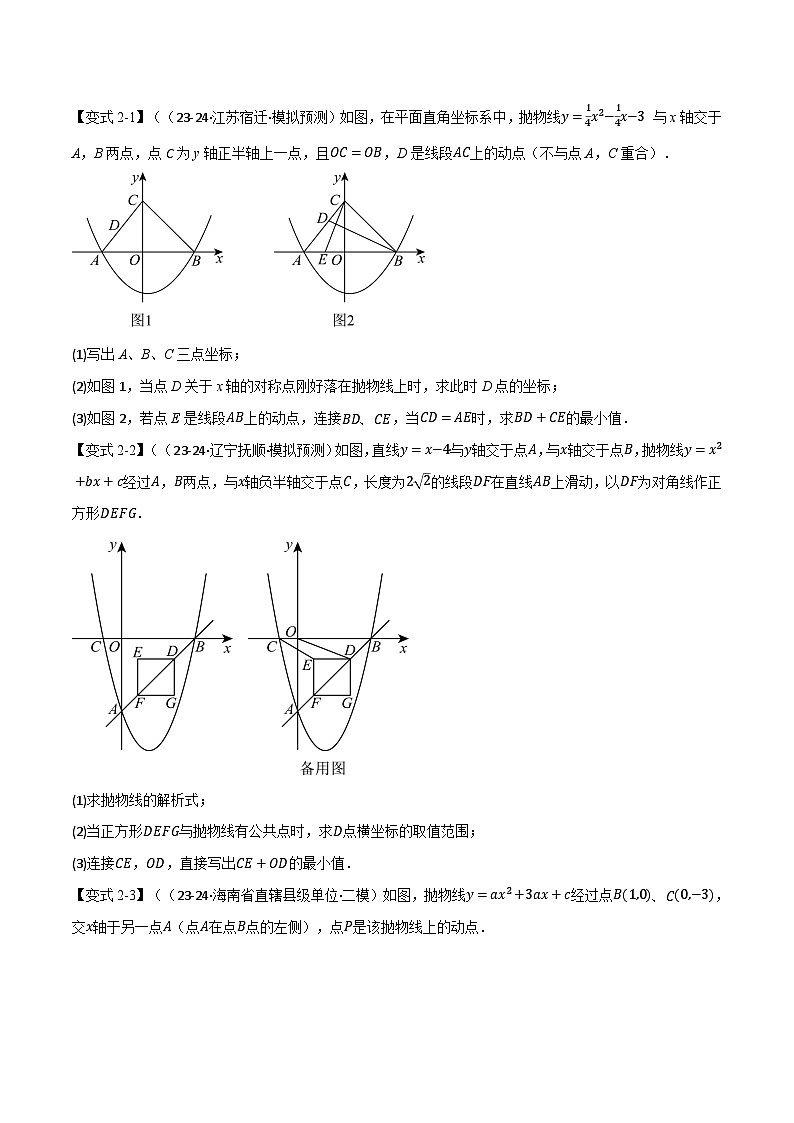
【变式2-1】（（23-24·江苏宿迁·模拟预测）如图，在平面直角坐标系中，抛物线y=14x2−14x−3 与x轴交于A，B两点，点C为y轴正半轴上一点，且OC=OB，D是线段AC上的动点（不与点A，C重合）．

(1)写出A、B、C三点坐标；
(2)如图1，当点D关于x轴的对称点刚好落在抛物线上时，求此时D点的坐标；
(3)如图2，若点E是线段AB上的动点，连接BD、CE，当CD=AE时，求BD+CE的最小值．
【变式2-2】（（23-24·辽宁抚顺·模拟预测）如图，直线y=x−4与y轴交于点A，与x轴交于点B，抛物线y=x2+bx+c经过A，B两点，与x轴负半轴交于点C，长度为22的线段DF在直线AB上滑动，以DF为对角线作正方形DEFG．
(1)求抛物线的解析式；
(2)当正方形DEFG与抛物线有公共点时，求D点横坐标的取值范围；
(3)连接CE，OD，直接写出CE+OD的最小值．
【变式2-3】（（23-24·海南省直辖县级单位·二模）如图，抛物线y=ax2+3ax+c经过点B1,0、C0,−3，交x轴于另一点A（点A在点B点的左侧），点P是该抛物线上的动点．
(1)求抛物线的解析式；
(2)当点P在直线AC下方且S△PAC=34S△AOC时，请求出点P的横坐标；
(3)在抛物线的对称轴l上是否存在点Q，使得QC+QB最小？若存在，请求出这个最小值；若不存在，请说明理由；
(4)若点E在x轴上，是否存在以P、A、C、E为顶点且以AC为一边的平行四边形？若存在，求点P的坐标；若不存在，请说明理由．
【题型3 周长的最值问题】
【例3】（（23-24·辽宁丹东·模拟预测）如图，对称轴为直线x=−1的抛物线y=a(x−ℎ)2+ka≠0图象与x轴交于点A、B(点A在点B的左侧)，与y轴交于点C，其中点B的坐标为2,0，点C的坐标为0,4．
(1)求该抛物线的解析式；
(2)如图1，若点P为抛物线上第二象限内的一个动点，点M为线段CO上一动点，当△APC的面积最大时，求△APM周长的最小值；
(3)如图2，将原抛物线绕点A旋转180°，得新抛物线y'，在新抛物线y'的对称轴上是否存在点Q使得△ACQ为等腰三角形？若存在，请直接写出点Q的坐标；若不存在，说明理由．
【变式3-1】（23-24九年级·山东淄博·期中）如图，在平面直角坐标系中，抛物线y=−14x2+bx+c与x轴交于A−2，0，B6，0两点，与y轴交于点C，点P为直线BC上方抛物线上一动点．
(1)求抛物线的解析式；
(2)过点A作AD∥BC交抛物线于D，若点E为对称轴上一动点，求△BED周长的最小值及此时点E的坐标；
(3)过点A作AD∥BC交抛物线于D，过点E为直线AD上一动点，连接CP，CE，BP，BE，求四边形BPCE面积的最大值及此时点P的坐标．
【变式3-2】（23-24九年级·全国·期末）如图抛物线y=ax2+bx+c经过点A(−1,0)，点C(0,3)，且OB=OC．
(1)求抛物线的解析式及其对称轴；
(2)点D、E是直线x=1上的两个动点，且DE=1，点D在点E的上方，求四边形ACDE的周长的最小值；
(3)点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为3:5两部分，求点P的坐标．
【变式3-3】（23-24九年级·广东广州·阶段练习）如图，在平面直角坐标系中，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，其中点A的坐标为−1,0，点C的坐标为0,−3．

(1)求抛物线的解析式；
(2)如图1，E为△ABC边AB上的一动点，F为BC边上的一动点，D点坐标为0,−2，
①求DE+EF的最小值②求△DEF周长的最小值；
(3)如图2，N为射线CB上的一点，M是地物线上的一点，M、N均在第一象限内，B、N位于直线AM的同侧，且AM∥CN，当△AMN为等腰三角形时，求点N的坐标．（直接写出点N的坐标，不要求写解答过程）
【题型4 面积的最值问题】
【例4】（23-24九年级·云南红河·期中）如图，抛物线y=ax2+bx−4与x轴交于A−3，0、B4，0两点，与y轴交于点C．
(1)求抛物线解析式；
(2)点H是抛物线对称轴上的一个动点，连接AH、CH，求出△ACH周长的最小值时点H的坐标；
(3)若点G是第四象限抛物线上的动点，求△BCG面积的最大值以及此时点G的坐标；
【变式4-1】（23-24九年级·甘肃武威·阶段练习）如图，抛物线y=ax2+bx+c与x轴交于点A−2,0和点B4,0，与y轴交于点C0,4．
(1)求抛物线的解析式．
(2)点D在抛物线的对称轴上，当AD+CD取得最小值时，求此时点D的坐标．
(3)点P是直线BC上方抛物线上一动点，连接CP、BP，求△PBC的面积的最大值，并求此时点P的坐标．
【变式4-2】（23-24九年级·山东·期末）如图所示，抛物线与x轴交于A、B两点，与y轴交于点C，且OA=1，OB=OC=4．

(1)求抛物线的解析式；
(2)若连接AC、BC．动点D从点A出发，在线段AB上以每秒1个单位长度向点B做匀速运动；同时，动点E从点B出发，在线段BC上以每秒2个单位长度向点C做匀速运动，当其中一点到达终点时，另一点随之停止运动，连接DE，设运动时间为t秒．在D、E运动的过程中，当t为何值时，四边形ADEC的面积最小，最小值为多少？
(3)点M是抛物线上位于x轴上方的一点，点N在x轴上，是否存在以点M为直角顶点的等腰直角三角形CMN？若存在，求出点M的坐标，若不存在，请说明理由．
【变式4-3】（23-24九年级·福建福州·期中）已知抛物线y=ax2+bx+ca≠0与y轴交于点A0,−5，顶点为B2,−1，过点C2,−5直线与抛物线交于D，E两点（点D在点E的左侧）．
(1)求抛物线的解析式；
(2)求△BDE面积的最小值；
(3)若D，E两点都在第四象限，过点D作直线y=−1的垂线，垂足为F，直线EB与直线DF交于点G，连接CF，求证：四边形BCFG是平行四边形．
【题型5 线段和差倍分的最值】
【例5】（23-24·山东济南·一模）抛物线y=−12x2+a−1x+2a与x轴交于Ab,0，B4,0两点，与y轴交于点C0,c，点P是抛物线在第一象限内的一个动点，且在对称轴右侧．
(1)求a，b，c的值；
(2)如图1，连接BC、AP，交点为M，连接PB，若S△PMBS△AMB=14，求点P的坐标；
(3)如图2，在（2）的条件下，过点P作x轴的垂线交x轴于点E，将线段OE绕点O逆时针旋转得到OE'，旋转角为α(0°<α<90°)，连接E'B，E'C，求E'B+34E'C的最小值．
【变式5-1】（23-24九年级·安徽合肥·阶段练习）如图，在平面直角坐标系中，抛物线y=−x2+23x的顶点为A点，且与x轴的正半轴交于点B．

（1）连接AO，AB，则△AOB为 三角形；
（2）P点为该抛物线对称轴上一点，当OP+12AP取最小值时，OP= ．
【变式5-2】（23-24九年级·安徽阜阳·阶段练习）已知抛物线与x轴相交于A，B两点，与y轴相交于点C0，6，顶点为D2，8．

(1)求此抛物线的解析式；
(2)如图1，点P为抛物线对称轴（直线l）上的动点，求当PB−PC取得最小值时点P的坐标；
(3)如图2，在第一象限内，抛物线上有一动点M，求△BCM面积的最大值．
【变式5-3】（23-24九年级·广东东莞·期中）如图，已知抛物线y=ax2+bx+c（a≠0）与y轴相交于点C0,−2，与x轴分别交于点B3,0和点A，且∠CAO=45°．
(1)求抛物线解析式；
(2)抛物线上是否存在一点Q，使得∠BAQ=∠ABC，若存在，请求出点Q坐标，若不存在，请说明理由；
(3)抛物线的对称轴交x轴于点D，在y轴上是否存在一个点P，使22PC+PD的值最小，若存在，请求出最小值，若不存在，请说明理由．
【题型6 由二次函数性质求二次函数的最值】
【例6】（23-24九年级·陕西西安·阶段练习）如图，抛物线y=ax2+bx+3与x轴交于点A1,0,B3,0，与y轴交于点C．

(1)求抛物线的解析式；
(2)点Mx1,y1,Nx2,y2是抛物线上不同的两点且x1+x2=4x1−x2，求y1−y2的最小值．
【变式6-1】（23-24九年级·江西赣州·期中）观察下列两个数的乘积，说明其中哪个积最大．
1×100,2×99,3×98,4×97,⋅⋅⋅,99×2,100×1．
【观察发现】（1）发现所列各组式子中两个因数的和都为_____________．
【问题解决】（2）若设其中一个因数为x（1≤x≤100，且为正整数），所列两个数的积为y，请说明哪个积最大，最大值是多少．
【拓展应用】（3）若大于0的a、b满足a+b=4，求a2+b2的最小值．
【变式6-2】（（23-24·贵州·模拟预测）已知二次函数y=ax2−4x+c（a≠0，a，c为常数）的图象经过点1,−6，−4,−1
(1)求二次函数的表达式；
(2)当−1≤x＜0时，求二次函数的最大值；
(3)当m≤x≤0时，二次函数的最大值与最小值的和为2m，求m的值．
【变式6-3】（23-24九年级·湖南长沙·开学考试）在平面直角坐标系中，我们将形如1,−1，−2.1,2.1这样，纵坐标与横坐标互为相反数的点称之为“互补点”．
(1)直线y=2x−3上的“互补点”的坐标为_________；
(2)直线y=kx+2k≠0上是否有“互补点”，若有，请求出点的坐标，若没有请说明理由；
(3)若函数y=14x2+n−k−1x+m+k−2的图象上存在唯一的一个“互补点”，且当−1≤n≤2时，m的最小值为k，求k的值．
【题型7 由二次函数的最值求字母的值】
【例7】（（23-24九年级·全国·专题练习）已知在平面直角坐标系中，设二次函数y1=x2+bx+a，y2=ax2+bx+1(a、b是实数，a≠0)．
(1)若函数y1的对称轴为直线x=3，且函数y1的图象经过点(a,−6)，求函数y1的表达式；
(2)若函数y1的图象经过点(r,0)，其中r≠0，求证：函数y2的图象经过点(1r，0)；
(3)设函数y1和函数y2的最小值分别为m和n，若m+n=0，求m、n的值．
【变式7-1】（23-24九年级·河南许昌·期末）如图，已知二次函数y=x2+ax+a−4的图象经过点P−2,−2．
(1)求a的值和二次函数图象的顶点坐标．
(2)已知点Qm,n在该二次函数图象上．
①当m=−3时，求n的值；
②当m≤x≤m+1时，该二次函数有最小值1，请结合函数图像求出m的值．
【变式7-2】（23-24九年级·湖南长沙·阶段练习）已知拋物线y=ax−ℎ2+k与x轴交于A，B两点（A在B的左边），与y轴交于点C．顶点为M．

(1)如图，若该拋物线可以由抛物线y=ax2先向右平移5个单位，在向上平移4个单位得到，点C坐标为0,−21．
（i）求A，B两点的坐标；
（ii）若线段AM的垂直平分线交x轴交于点D，交y轴交于点E，交AM交于点P，求证：四边形ADME是菱形；
(2)已知a=1，抛物线顶点M在直线y=2x−5上，若在自变量x的值满足2ℎ≤x≤2ℎ+3的情况下，对应函数值y的最小值为14，求h的值．
【变式7-3】（（23-24·广西贺州·二模）如图，在平面直角坐标系中，已知抛物线y=ax2+bx−3与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，且OB=3OA=3．

(1)求这个二次函数的解析式；
(2)若点M是线段BC下方抛物线上的一个动点（不与点B，点C重合），过点M作直线MN⊥x轴于点D，交线段BC于点N．是否存在点M使得线段MN的长度最大，若存在，求线段MN长度的最大值，若不存在，请说明理由；
(3)当二次函数y=ax2+bx−3的自变量x满足t≤x≤t+1时，此函数的最大值与最小值的差为2，求出t的值．
【题型8 由二次函数的最值求字母的取值范围】
【例8】（23-24九年级·江苏南通·阶段练习）用好错题本可以有效的积累解题策略，减少再错的可能．下面是小颖同学错题本上的一道题，请仔细阅读，并完成相应任务．
任务一：请帮助小颖完成上述错题订正；
任务二：若点M2,y3也是此抛物线上的点，记抛物线在A，M之间的部分为图象G（包括M，A两点），记图形G上任意一点的纵坐标的最大值与最小值的差为t，若t≥y2−y1，直接写出m的取值范围．
【变式8-1】（23-24九年级·河南郑州·阶段练习）如图，已知二次函数y=−x2+bx+c的图象经过点A4,1，点B0,5．

(1)求该二次函数的表达式，并求出对称轴和顶点坐标；
(2)点Cm,n在该二次函数图象上，当m≤x≤4时，n的最大值为294，最小值为1，请根据图象直接写出m的取值范围．
【变式8-2】（（23-24·浙江温州·模拟预测）已知二次函数y=ax2−2ax+3图象的一部分如图所示，它经过−1,0．
(1)求这个二次函数的表达式，并在图中补全该图象；
(2)当−2≤x≤t时，函数的最大值为m，最小值为n，若m−n=9，求t的取值范围．
【变式8-3】（23-24九年级·湖北·周测）已知抛物线y=x2+bx+c经过点B，与y轴交于点A，顶点P在直线OB上．如图1，若点B的坐标为3,6，点P的横坐标为1．
(1)试确定抛物线的解析式；
(2)若当m≤x≤4时，y=x2+bx+c的最小值为2，最大值为11，请求出m的取值范围；
(3)已知：点M在抛物线上，点N的坐标为2,3，且∠MNA=∠BAN，请直接写出符合题意的点M的坐标．
*年*月*日 星期天
错题***
在平面直角坐标系中，抛物线y=x2−2mx+m2+1存在两点Am−1,y1，Bm+2,y2.
①求此抛物线的对称轴；（用含m的式子表示）
②记抛物线在A，B之间的部分为图象F（包括A，B两点），y轴上一动点C(0,a)，过点C作垂直于y轴的直线l与F有且仅有一个交点，求a的取值范围；
专题21.9 二次函数中的最值问题【八大题型】
【沪科版】
TOC \ "1-3" \h \u
\l "_Tc17744" 【题型1 几何图形中线段最值问题】 PAGEREF _Tc17744 \h 1
\l "_Tc1983" 【题型2 两线段和的最值问题】 PAGEREF _Tc1983 \h 7
\l "_Tc25836" 【题型3 周长的最值问题】 PAGEREF _Tc25836 \h 19
\l "_Tc31085" 【题型4 面积的最值问题】 PAGEREF _Tc31085 \h 31
\l "_Tc11133" 【题型5 线段和差倍分的最值】 PAGEREF _Tc11133 \h 41
\l "_Tc11136" 【题型6 由二次函数性质求二次函数的最值】 PAGEREF _Tc11136 \h 51
\l "_Tc31248" 【题型7 由二次函数的最值求字母的值】 PAGEREF _Tc31248 \h 56
\l "_Tc12038" 【题型8 由二次函数的最值求字母的取值范围】 PAGEREF _Tc12038 \h 64
【题型1 几何图形中线段最值问题】
【例1】（23-24九年级·广西钦州·期中）如图，线段AB=10，点P在线段AB上，在AB的同侧分别以AP,BP为边长作正方形APCD和BPEF，点M，N分别是EF，CD的中点，则MN的最小值是（ ）
A．2B．3C．5D．6
【答案】C
【分析】设MN=y，PC=x，根据正方形的性质和勾股定理列出y2关于x的二次函数关系式，求二次函数的最值即可．
【详解】解：作MG⊥DC交DC延长线于G，则四边形CEMG为矩形，
∴CG=EM=12EF=12BP．
∵N是CD的中点，
∴CN=12CD=12AP，
∴NG=CG+CN=12AP+BP=12AB=5．
设MN=y，PC=x，则MG=CE=10−2x，
在Rt△MNG中，由勾股定理得：MN2=MG2+GN2，
即y2=52+10−2x2．
∵0∴当10−2x=0，即x=5时，y2最小值=25，
∴y最小值=5．即MN的最小值为5；
故选C．
【点睛】本题考查了正方形的性质，矩形的判定与性质，勾股定理，二次函数的最值．熟练掌握勾股定理和二次函数的最值是解决问题的关键．
【变式1-1】（23-24九年级·安徽合肥·阶段练习）如图，AB=6，点C是AB上的动点，以AC、BC为边在AB同侧作等边三角形，M、N分别是CD、BE中点，MN最小值=（ ）
A．3B．32C．322D．332
【答案】D
【分析】本题主要考查了等边三角形的性质，勾股定理，二次函数的最值问题，如图所示，连接CN，根据等边三角形的性质得到∠ACD=∠BCE=60°，∠BCN=12∠BCE=30°，BN=12BE=12BC，进而推出∠MCN=90°，设AC=2x，则BC=6−2x，BN=3−x，利用勾股定理得到CN2=3x2−18x+27，则MN2=4x−942+274，利用二次函数的性质求出MN2的最小值，即可求出MN的到最小值．
【详解】解：如图所示，连接CN，
∵△BCE，△ACD是等边三角形，点N是BE的中点，
∴∠ACD=∠BCE=60°，∠BCN=12∠BCE=30°，BN=12BE=12BC，
∴∠MCN=180°−∠ACD−∠BCN=90°，
设AC=2x，则BC=6−2x，
∴BN=3−x，
∴CN2=BC2−BN2=6−2x2−3−x2=3x2−18x+27，
∵点M是CD的中点，
∴CM=12CD=12AC=x，
∴MN2=CM2+CN2=x2+3x2−18x+27=4x−942+274，
∵4>0，
∴当x=94时，MN2有最小值274，
∴MN有最小值332，
故选D．
【变式1-2】（23-24九年级·广东江门·阶段练习）如图，在矩形ABCD中，AB=3，BC=4，将对角线AC绕对角线交点O旋转，分别交边AD、BC于点E、F，点P是边DC上的一个动点，且保持DP=AE，连接PE、PF，设AE=x0(1)填空：PC= ，FC= ；（用含x的代数式表示）
(2)若△PEF的面积为S，求S与x的函数关系及△PEF面积的最小值；
(3)在运动过程中，PE⊥PF是否成立？若成立，求出x的值；若不成立，请说明理由．
【答案】(1)3−x，x
(2)S=x−742+4716，4716
(3)不成立，理由见详解
【分析】（1）由矩形的性质可得AD∥BC，DC=AB=3，AO=CO，可证△AEO≌△CFO，可得AE=CF=x，由DP=AE=x，可得PC=3−x；
（2）由S△EFP=S梯形EDCF−S△DEP−S△CFP，可得S△EFP=x2−72x+6=x−742+4716，根据二次函数的性质可求△PEF面积的最小值；
（3）若PE⊥PF，则可证△DPE≌△CFP，可得DE=CP，即3−x=4−x，方程无解，则不存在x的值使PE⊥PF．
【详解】（1）解：∵四边形ABCD是矩形
∴AD∥BC，DC=AB=3，AO=CO
∴∠DAC=∠ACB，且AO=CO，∠AOE=∠COF
∴△AEO≌△CFOASA
∴AE=CF
∵AE=x，且DP=AE
∴DP=x，CF=x，DE=4−x，
∴PC=CD−DP=3−x
故答案为：3−x ，x
（2）解：依题意
∵S△EFP=S梯形EDCF−S△DEP−S△CFP，
∴S△EFP=x+4−x×32−12x⋅4−x−12x⋅3−x=x2−72x+6=x−742+4716
∵△PEF的面积为S，
∴S与x的函数关系S=x−742+4716
∴开口向上，当x=74时，△PEF面积的最小值为4716
（3）解：不成立
理由如下：若PE⊥PF，则∠EPD+∠FPC=90°
又∵∠EPD+∠DEP=90°
∴∠DEP=∠FPC，且CF=DP=AE，∠EDP=∠PCF=90°
∴△DPE≌△CFPAAS
∴DE=CP
∴3−x=4−x
则方程无解，
∴不存在x的值使PE⊥PF，
即PE⊥PF不成立．
【点睛】本题是四边形综合题，考查了矩形的性质，列代数式表达式、全等三角形的判定和性质，二次函数的性质，熟练运用这些性质进行推理是本题的关键．
【变式1-3】（23-24九年级·广东广州·期中）如图，在正方形ABCD中，AB=7，F是边CD上的动点，将△ADF绕点A顺时针旋转90°至△ABE，将△ADF沿AF翻折至△AGF，连接EF、BD交于点H，连接GH，则△EGH面积的最大值为 ．
【答案】4916
【分析】根据正方形的性质和旋转的性质可得∠DAF+∠FEC=∠AEF，
连接BF，作FQ⊥CD交 BD于 Q， HM⊥BC于 M，连接BF,BG，设BF交EG于点 O．证出△AEG≌△AFB，可得EG=BF，再证明△EFG≌△FEB，可得∠GEF=∠EFB，同理∠FBG=∠EGB，从而得到∠EFB=∠FBG，设DF=EB=x，则CF=7−x，再证出△FQH≌△EBH，列出含x的面积公式，利用二次函数配方即可得到最大值．
【详解】解：∵四边形ABCD是正方形，
∴AD∥BC，
∴∠DAE+∠AEC=180°，
∴∠DAF+∠EAF+∠AEF+∠FEC=180°，
∵将△ADF绕点A顺时针旋转90°至△ABE，
∴∠EAF=90°,AE=AF，
∴∠AEF=45°，
∴∠DAF+∠FEC=45°，
∴∠DAF+∠FEC=∠AEF，
连接BF，作FQ⊥CD交 BD于 Q， HM⊥BC于 M，连接BF,BG，设BF交EG于点 O．
∵四边形ABCD是正方形，
∴AB=BC=CD=7,∠C=90°，
∵∠DAF=∠FAG=∠BAE，
∴∠EAG=∠FAB，
∵AE=AF,AG=AB，
∴△AEG≌△AFBSAS，
∴EG=BF，
∵EG=BF,EF=FE,FG=EB，
∴△EFG≌△FEBSSS，
∴∠GEF=∠EFB，
同理∠FBG=∠EGB，
∵∠EOF=∠BOG，
∴∠EFB=∠FBG，
∴EF∥BG，
∴S△EQG=S△EBQ，
设DF=EB=x，则CF=7−x，
∵FQ∥BE,FQ=DF=EB，
∴∠FQH=∠EBH，
∵∠QHF=∠EHB，
∴△FQH≌△EBHAAS，
∴FH=EH，
∵HM∥CF，
∴EM=MC，
∴HM=12CF=127−x，
∴S△EHG=S△EBH=12×12x7−x=−14x2−7x=−14x−722+4916，
∵−14<0，
∴x=72时，△EHG的面积最大，最大值为4916．
故答案为：4916．
【点睛】本题考查的知识点是全等三角形的判定及二次函数的运用，解题的关键是熟练的掌握全等三角形的判定及二次函数的运用．
【题型2 两线段和的最值问题】
【例2】（（23-24·安徽合肥·一模）如图，直线y=−x＋3与x轴、y轴分别交于B、C两点，抛物线y=−x2+bx+c经过点B、C，与x轴另一交点为A，顶点为D．
(1)求抛物线的解析式；
(2)在x轴上找一点E，使EC+ED的值最小，求EC+ED的最小值；
(3)在抛物线的对称轴上是否存在一点P，使得∠APB=∠OCB？若存在，求出P点坐标，若不存在，请说明理由．
【答案】(1)y=−x2+2x+3
(2)点E37，0，则EC+ED的最小值为52
(3)点P的坐标为1,2+22或1,−2−22
【分析】（1）直线y=−x+3与x轴、y轴分别交于B、C两点，则点B、C的坐标分别为3,0、0,3，将点B、C的坐标代入二次函数表达式，即可求解；
（2）如图1，作点C关于x轴的对称点C'，连接CD'交x轴于点E，则此时EC+ED为最小，即可求解；
（3）分点P在x轴上方、点P在x轴下方两种情况，分别求解．
【详解】（1）解：对于直线y=−x+3，
当x=0时，y=3；当y=0时，−x+3=0，则x=3；
∴B3,0、C0,3
将点B3,0、C0,3代入二次函数表达式得：−9+3b+c=0c=3，
解得：b=2c=3，
故函数的表达式为：y=−x2+2x+3；
（2）如图1中，作点C关于x轴的对称点C'，连接CD'交x轴于点E，则此时EC+ED为最小，此时，点C'的坐标为0,−3，
又y=−x2+2x+3=−x−12+4，
∴函数顶点D坐标为1,4，
设直线C'D的表达式为y=kx+b，
将C'0,−3、D1,4代入一次函数表达式得：k+b=4b=−3，
解得，k=7b=−3，
∴直线C'D的表达式为：y=7x−3，
当y=0时，7x−3=0，解得x=37，
故点E37，0，
则EC+ED的最小值为DC'=1+4+32=52；
（3）解：对于y=−x2+2x+3，令y=0，则−x2+2x+3=0，
解得，x=−1或x=3，
∴点A的坐标为−1,0；
又B3,0，
∴AB=3−−1=4；
①当点P在x轴上方时，如图2中，
∵OB=OC=3，则∠OCB=45°=∠APB，
∴∠PAB=∠PBA=12180°−45°=67.5°，∠APD=12∠APB=22.5°
过点B作BH⊥AP于点H，
∴∠ABH=90°−∠PAB=22.5°
∴∠HBP=∠PBA−∠ABH=67.5°−22.5°=45°=∠APB
∴BH=PH,
设PH=BH=m
则PB=PA=2m，
∴AH=PA−PH= 2−1m
由勾股定理得：AB2=AH2+BH2，
∴16=m2+2−1m2，
解得：m2=8+42，
则PB2=2m2=16+82
则yP=PB2−22=2+22；
②当点P在x轴下方时，同理可得yP=−2+22；
故点P的坐标为1,2+22或1,−2−22．
【点睛】本题考查的是二次函数综合运用，涉及到一次函数、等腰三角形性质、点的对称性等，其中（3）要注意分类求解，避免遗漏．
【变式2-1】（（23-24·江苏宿迁·模拟预测）如图，在平面直角坐标系中，抛物线y=14x2−14x−3 与x轴交于A，B两点，点C为y轴正半轴上一点，且OC=OB，D是线段AC上的动点（不与点A，C重合）．

(1)写出A、B、C三点坐标；
(2)如图1，当点D关于x轴的对称点刚好落在抛物线上时，求此时D点的坐标；
(3)如图2，若点E是线段AB上的动点，连接BD、CE，当CD=AE时，求BD+CE的最小值．
【答案】(1)A−3,0，B4,0，C0,4
(2)−43,209
(3)97
【分析】（1）根据题意y=14x2−14x−3y=0得x=4y=0，x=−3y=0，结合OC=OB写出A、B、C三点坐标即可；
（2）设直线AC的解析式为y=kx+b，把A−3,0，C0,4分别代入解析式，确定直线的解析式，设点Dm,43m+4，对称点坐标为D'm,−43m−4，代入抛物线解析式y=14x2−14x−3中，计算解答即可；
（3）过点C作CP∥x轴，且使得CP=CA，连接PB,PD，利用三角形全等，把线段和最小值转化为三角形不等式，解答即可．
本题考查了抛物线与x轴的交点，待定系数法求解析式，三角形全等的判定与性质，三角形不等式求最值，熟练掌握相关知识，特别是三角形不等式是解题的关键．
【详解】（1）根据题意得y=14x2−14x−3y=0，
解得x=4y=0，x=−3y=0，
∴A−3,0，B4,0，
∴OB=4,
∵OC=OB，
∴C0,4．
（2）设直线AC的解析式为y=kx+b，
把A−3,0，C0,4分别代入解析式，得
−3k+b=0b=4，
故直线AC的解析式为y=43x+4，
设点Dm,43m+4，
则其对称点坐标为D'm,−43m−4，
代入抛物线解析式y=14x2−14x−3中，得
14m2−14m−3=−43m−4，
整理，得3m2+13m+12=0，
解方程，得m=−43,m=−3(舍去)，
当m=−43时，y=−43×43+4=209，
故D−43,209．
（3）过点C作CP∥x轴，且使得CP=CA，连接PB,PD，

∵A−3,0，C0,4，
∴AC=−3−02+0−42=5，
∴CP=CA=5，
∴P−5,4，
∵ B4,0，
∴PB=−5−42+4−02=97．
∵CP∥x轴，
∴∠PCD=∠CAE，
∵CP=CA，
∵PC=CA∠PCD=∠CAECD=AE
∴△PCD≌△CAESAS
∴PD=CE，
∴BD+CE的最小值变成了BD+PD的最小值，
∵BD+PD≥PB，
故当点P，D，B三点共线时，BD+PD取得最小值，且最小值为PB，
∴BD+CE的最小值为97．
【变式2-2】（（23-24·辽宁抚顺·模拟预测）如图，直线y=x−4与y轴交于点A，与x轴交于点B，抛物线y=x2+bx+c经过A，B两点，与x轴负半轴交于点C，长度为22的线段DF在直线AB上滑动，以DF为对角线作正方形DEFG．
(1)求抛物线的解析式；
(2)当正方形DEFG与抛物线有公共点时，求D点横坐标的取值范围；
(3)连接CE，OD，直接写出CE+OD的最小值．
【答案】(1)y=x2−3x−4
(2)0≤m≤4+6
(3)5
【分析】（1）由y=x−4得A0,−4，B4,0，再用待定系数法可得抛物线的解析式为y=x2−3x−4；
（2）根据DF=22，四边形DEFG是正方形，得DE=EF=FG=DG=2，设Dm,m−4，则Em−2,m−4；当正方形DEFG与抛物线y=x2−3x−4有唯一公共点E时，m−4=(m−2)2−3m−2−4，可得此时D4+6,6；当正方形DEFG与抛物线y=x2−3x−4有唯一公共点D时，可得此时D0,−4；画出图形可得答案；
（3）求出C−1,0；设Dt,t−4，则Et−2,t−4，CE+OD=2×(t−52)2+94+(t−2)2+4，(t−52)2+94+(t−2)2+4可看作x轴上的点Rt,0到点K52,32和点T2,−2的距离之和，当K，R，T共线时，(t−52)2+94+(t−2)2+4取最小值，求出KT可得答案．
【详解】（1）解：在y=x−4中，令x=0得y=−4，令y=0得x=4，
∴A0,−4，B4,0，
把A0,4，B4,0代入y=x2+bx+c得：
c=−416+4b−4=0，
解得：b=−3c=−4，
∴抛物线的解析式为y=x2−3x−4；
（2）解：∵DF=22，四边形DEFG是正方形，
∴DE=EF=FG=DG=2，
设Dm,m−4，则Em−2,m−4；
当正方形DEFG与抛物线y=x2−3x−4有唯一公共点E时，如图：

把Em−2,m−4代入y=x2−3x−4得：
m−4=(m−2)2−3m−2−4，
解得m=4+6或m=4−6(在B左侧，舍去)；
此时D4+6,6；
当正方形DEFG与抛物线y=x2−3x−4有唯一公共点D时，如图：

把Dm,m−4代入y=x2−3x−4得：
m−4=m2−3m−4，
解得：m=0或m=4(与B重合，舍去)，
此时D0,−4；
由图可知，当0≤m≤4+6时，正方形DEFG与抛物线有公共点；
∴当正方形DEFG与抛物线有公共点时，D点横坐标的取值范围是0≤m≤4+6；
（3）解：在y=x2−3x−4中，令y=0得：0=x2−3x−4，
解得：x=4或x=−1，
∴C−1,0；
设Dt,t−4，则Et−2,t−4，
∴CE=(t−1)2+(t−4)2=2t2−10t+17=2×(t−52)2+94，
OD=t2+(t−4)2=2t2−8t+16=2×(t−2)2+4，
∴CE+OD=2×(t−52)2+94+(t−2)2+4，
当(t−52)2+94+(t−2)2+4最小时，CE+OD取最小值，
而(t−52)2+94+(t−2)2+4可看作x轴上的点Rt,0到点K52,32和点T2,−2的距离之和，如图：
∴当K，R，T共线时，(t−52)2+94+(t−2)2+4取最小值，最小值为KT的长，
∵KT=(52−2)2+(32+2)2=522，
∴(t−52)2+94+(t−2)2+4的最小值为522，
∵2×522=5，
∴CE+OD的最小值为5．
【点睛】本题考查二次函数的综合应用，涉及待定系数法，正方形性质及应用，最短路径等知识，解题的关键是用含字母的代数式表示相关点坐标和相关线段的长度．
【变式2-3】（（23-24·海南省直辖县级单位·二模）如图，抛物线y=ax2+3ax+c经过点B1,0、C0,−3，交x轴于另一点A（点A在点B点的左侧），点P是该抛物线上的动点．
(1)求抛物线的解析式；
(2)当点P在直线AC下方且S△PAC=34S△AOC时，请求出点P的横坐标；
(3)在抛物线的对称轴l上是否存在点Q，使得QC+QB最小？若存在，请求出这个最小值；若不存在，请说明理由；
(4)若点E在x轴上，是否存在以P、A、C、E为顶点且以AC为一边的平行四边形？若存在，求点P的坐标；若不存在，请说明理由．
【答案】(1)y=34x2+94x−3
(2)−1或−3
(3)存在，5
(4)存在，P1−3,−3，P2−3−412,3,P3−3+412,3
【分析】
对于（1），直接将点B，C的坐标代入关系式得出方程组，再求出解即可；
对于（2），先求出点A，C的坐标，进而求出直线的关系式，再求出S△AOC，可知S△PAC，
作PK∥y轴，交AC于点K，设P，K的坐标，并表示出PK，然后根据面积相等列出方程，并求出解；
对于（3），先确定QC+QB最小时Q的位置，再根据勾股定理求出答案；
对于（4），①当点P在x轴下方时，有P1C∥AE1，根据yp=−3可求出答案；
②当点P在x轴上方时，PC与AE是平行四边形的对角线，设点E，P的坐标，再根据对角线交点的坐标相同得出方程，求出解可得答案．
【详解】（1）
∵抛物线y=ax2+3ax+c经过点B1,0、C0,−3，
∴a+3a+c=0c=−3，
解得a=34c=−3，
∴抛物线的解析式为y=34x2+94x−3；
（2）
令y=0，则=34x2+94x−3=0，
则x1=−4,x2=1，
∴A−4,0，
设直线AC表达式为yAC=kx+b，又C0,−3，
∴−4k+b=0b=−3，
解得k=−34b=−3，
∴yAC=−34x−3，
∵A−4,0,C0,−3，
∴OA=4,OC=3，
∴S△AOC=6，
∴当S△PAC=34S△AOC时，S△PAC=92，
作PK⊥x轴，交AC于点K，
设Pm,34m2+94m−3，则Km,−34m−3
则PK=yE−yP=−34m2−3m，
则12xC−xAPK=92，m2+4m+3=0，
∴m1=−1,m2=−3．
即点P的横坐标为−1或−3．
（3）
存在，
∵点A与点B关于对称轴l对称，
∴当点Q在直线AC与对称轴l交点处时QC+QB最小，
此时QC+QB=QC+QA=AC，
由（2）知OA=4,OC=3，
∴AC=5，所以这个最小值为5．
（4）
存在，设Pm,34m2+94m−3，
①当点P在x轴下方时，有P1C∥AE1，
∵C0,−3,
∴yp=−3，
则34m2+94m−3=−3，
∴m1=0（舍去），m2=−3，
∴P1−3,−3
②当点P在x轴上方时，PC与AE是平行四边形的对角线，
设En,0,Pm,34m2+94m−3，
∵A−4,0,C0,−3，
∴m+0=n−434m2+94m−3−3=0，
则m1=−3−412,m2=−3+412，
又34m2+94m−3−3=0，
∴34m2+94m−3=3，即yP=3，
∴P2−3−412,3,P3−3+412,3
综上所述，存在3个点：P1−3,−3，P2−3−412,3,P3−3+412,3．
【点睛】
本题主要考查了求二次函数的关系式，求一次函数的关系式，解一元二次方程，勾股定理，根据轴对称求线段和最小，平行四边形的性质，注意多种情况讨论，不要丢解．
【题型3 周长的最值问题】
【例3】（（23-24·辽宁丹东·模拟预测）如图，对称轴为直线x=−1的抛物线y=a(x−ℎ)2+ka≠0图象与x轴交于点A、B(点A在点B的左侧)，与y轴交于点C，其中点B的坐标为2,0，点C的坐标为0,4．
(1)求该抛物线的解析式；
(2)如图1，若点P为抛物线上第二象限内的一个动点，点M为线段CO上一动点，当△APC的面积最大时，求△APM周长的最小值；
(3)如图2，将原抛物线绕点A旋转180°，得新抛物线y'，在新抛物线y'的对称轴上是否存在点Q使得△ACQ为等腰三角形？若存在，请直接写出点Q的坐标；若不存在，说明理由．
【答案】(1)y=−12(x+1)2+92
(2)213+25
(3)存在，−7,23或−7,−23或−7,7
【分析】（1）根据对称轴为直线x=−1，可得ℎ=−1，再把点2,0，0,4代入解析式即可求解；
（2）过点P作AC的平行线PN，当直线PN与抛物线只有一个交点时，△APC面积最大，由此可对称点P的坐标；再根据轴对称最值问题可求出△APM周长的最小值；
（3）由1可得原抛物线的顶点坐标，由旋转的性质可得y'的顶点坐标，进而可求出y'的对称轴；则需要分类讨论①当AC=AQ时；②当CA=CQ时；③当QA=QC时，分别建立方程求解即可．
【详解】（1）解：∵抛物线y=a(x−ℎ)2+ka≠0的对称轴为直线x=−1，
∴x=ℎ=−1，
∵抛物线过点B2,0，点C0,4，
∴a(2+1)2+k=0a(0+1)2+k=4，
解得：a=−12k=92，
∴抛物线的解析式为：y=−12(x+1)2+92．
（2）由（1）知函数解析式为：y=−12(x+1)2+92．
∴A−4,0，
∴直线AC：y=x+4，
过点P作PN∥AC，设直线PN的解析式为：y=x+m，
当△APC的面积最大时，直线PN与抛物线有且仅有一个交点，
令x+m=−12(x+1)2+92，整理得x2+4x+2m−8=0，
∴Δ=42−42m−8=0，
解得：m=6，
∴x2+4x+4=0，
∴x=−2，即P−2,4；
作点A关于y轴的对称点A'，连接A'P交y轴于点M，如图1，此时△APM的周长最小，
∵A−4,0，
∴A'4,0，
∴A'P=(−2−4)2+(4−0)2=213，AP=(−2+4)2+(−4−0)2=25，
∴△APM周长的最小值为：213+25．
（3）由（1）知原抛物线的顶点坐标D(−1,92)，绕点A旋转后的顶点D'−7,−92，
∴y'的对称轴为直线x=−7；
设点Q的坐标为(−7,t)，
若△ACQ是等腰三角形，则需要分类讨论：
①当AC=AQ时，如图2；
∴(−4−0)2+(0−4)2=(−4+7)2+(0−t)2，解得t=±23；
∴Q(−7,23)或(−7,−23)；
②当CA=CQ时；
∴(−4−0)2+(0−4)2=(0+7)2+(4−t)2，无解；
③当QA=QC时，如图3，
∴(−4+7)2+(0−t)2=(0+7)2+(4−t)2，解得t=7，
∴Q(−7,7)．
综上可知，存在，点Q的坐标为−7,23或−7,−23或−7,7．
【点睛】本题属于二次函数综合题，涉及待定系数法求函数解析式，三角形的面积最值问题，轴对称最值问题，等腰三角形存在性问题，（2）关键是求出点P的坐标；（3）关键是进行正确的分类讨论，根据两点间距离公式建立方程．
【变式3-1】（23-24九年级·山东淄博·期中）如图，在平面直角坐标系中，抛物线y=−14x2+bx+c与x轴交于A−2，0，B6，0两点，与y轴交于点C，点P为直线BC上方抛物线上一动点．
(1)求抛物线的解析式；
(2)过点A作AD∥BC交抛物线于D，若点E为对称轴上一动点，求△BED周长的最小值及此时点E的坐标；
(3)过点A作AD∥BC交抛物线于D，过点E为直线AD上一动点，连接CP，CE，BP，BE，求四边形BPCE面积的最大值及此时点P的坐标．
【答案】(1)y=−14x2+x+3
(2)△BED的周长最小为55+29，E的坐标为2，−2
(3)四边形BPCE的面积最大为754，此时P3，154
【分析】（1）把A−2，0，B6，0两点代入抛物线的解析式得到−14×4−2b+c=0−14×36+6b+c=0，求解即可得出答案；
（2）求得C0，3，待定系数法求出直线BC的解析式为y=−12x+3，从而得出直线AD的解析式为y=−12x−1，联立y=−12x−1y=−14x2+x+3得出D8，−5，A，B关于抛物线的对称轴对称，直线AD与对称轴的交点即为点E，此时EA=EB，△BED的周长为BE+DE+BD=AD+BD最小，求出AD=55，BD=29，即可得解；
（3）过点P作x轴的垂线，交直线BC于点Q，设点P的坐标为m，−14m2+m+3，则Qm，−12m+3，则PQ=−14m2+m+3−−12m+3=−14m2+32m，求出S四边形BPCE=S△BCE+S△BCP=−34m2+92m+12，由二次函数的性质即可得出答案．
【详解】（1）解：∵抛物线y=−14x2+bx+c与x轴交于A−2，0，B6，0两点，
∴−14×4−2b+c=0−14×36+6b+c=0，
解得b=1c=3，
∴抛物线的解析式为：y=−14x2+x+3；
（2）解：由抛物线y=−14x2+x+3可得，当x=0时，y=3，
∴C0，3，对称轴为直线x=−12×−14=2，
设直线BC的解析式为y=kx+p，代入点B，点C的坐标得，p=36k+p=0，
解得k=−12p=3，
∴直线BC的解析式为y=−12x+3，
∵AD∥BC，
∴可设直线AD的解析式为y=−12x+q，代入点A的坐标得，−12×−2+q=0，
解得q=−1，
∴直线AD的解析式为y=−12x−1，
联立y=−14x2+x+3得y=−12x−1y=−14x2+x+3，
解得x=8y=−5或x=−2y=0，
∴D8，−5，
∵如图，A，B关于抛物线的对称轴对称，
∴直线AD与对称轴的交点即为点E，此时EA=EB，
∴EB+ED=EA+ED=AD最小，
∴△BED的周长为BE+DE+BD=AD+BD最小，
∵直线AD的解析式为y=−12x−1，当x=2时，y=−2，
∴E的坐标为2，−2，
∵AD=−2−82+0−−52=55，BD=8−62+−5−02=29，
∴△BED的周长最小为55+29；
（3）解：如图，过点P作x轴的垂线，交直线BC于点Q，
设点P的坐标为m，−14m2+m+3，则Qm，−12m+3，其中0∴PQ=−14m2+m+3−−12m+3=−14m2+32m，
∵AD∥BC，
∴S△BCE=S△BCA=12×8×3=12，
∴S四边形BPCE=S△BCE+S△BCP=12×6−14m2+32m+12=−34m2+92m+12，
∵−34<0，
∴当m=−922×−34=3时，四边形BPCE的面积最大为754，此时P3，154．
【点睛】本题主要考查了待定系数法求二次函数解析式、二次函数的综合应用、勾股定理、待定系数法求一次函数解析式等知识点，熟练掌握以上知识点并灵活运用，添加适当的辅助线是解此题的关键．
【变式3-2】（23-24九年级·全国·期末）如图抛物线y=ax2+bx+c经过点A(−1,0)，点C(0,3)，且OB=OC．
(1)求抛物线的解析式及其对称轴；
(2)点D、E是直线x=1上的两个动点，且DE=1，点D在点E的上方，求四边形ACDE的周长的最小值；
(3)点P为抛物线上一点，连接CP，直线CP把四边形CBPA的面积分为3:5两部分，求点P的坐标．
【答案】(1)抛物线的表达式为：y=−x2+2x+3，函数的对称轴为：x=1；
(2)10+1+13
(3)点P的坐标为4，−5或8，−45．
【分析】
（1）OB=OC，则点B(3,0)，则抛物线的表达式为：y=a(x+1)(x−3)=ax2−2ax−3a，即可求解；
（2）CD+AE=A'D+DC'，则当A'、D、C'三点共线时，CD+AE=A'D+DC'最小，周长也最小，即可求解；
（3）SΔPCB:SΔPCA=12EB×(yC−yP):12AE×(yC−yP)=BE:AE，即可求解．
【详解】（1）
解：∵OB=OC，∴点B(3,0)，
则抛物线的表达式为：y=a(x+1)(x−3)=a(x2−2x−3)=ax2−2ax−3a，
故−3a=3，解得：a=−1，
故抛物线的表达式为：y=−x2+2x+3①，
函数的对称轴为：x=1；
（2）
解：四边形ACDE的周长=AC+DE+CD+AE，其中AC=10、DE=1是常数，
故CD+AE最小时，周长最小，
取点C关于直线x=1对称点C'(2,3)，则CD=C'D，
取点A'(−1,1)，则A'D=AE，
故：CD+AE=A'D+DC'，则当A'、D、C'三点共线时，CD+AE=A'D+DC'最小，周长也最小，
四边形ACDE的周长的最小值=AC+DE+CD+AE
=10+1+A'D+DC'
=10+1+A'C'
=10+1+13；
（3）
解：如图，设直线CP交x轴于点E，
直线CP把四边形CBPA的面积分为3:5两部分，
又∵SΔPCB:SΔPCA=12EB×(yC−yP):12AE×(yC−yP)=BE:AE，
则BE:AE=3:5或5:3，
则AE=52或32，
即：点E的坐标为32，0或12，0，
将点E的坐标代入直线CP的表达式：y=kx+3，
解得：k=−6或−2，
故直线CP的表达式为：y=−2x+3或y=−6x+3②
联立①②并解得：x=4或8（不合题意值已舍去），
故点P的坐标为4，−5或8，−45．
【点睛】
本题考查的是二次函数综合运用，涉及到一次函数、图象面积计算、点的对称性等，通过确定点A'点来求最小值，是本题的难点．
【变式3-3】（23-24九年级·广东广州·阶段练习）如图，在平面直角坐标系中，抛物线y=x2+bx+c与x轴交于A、B两点，与y轴交于点C，其中点A的坐标为−1,0，点C的坐标为0,−3．

(1)求抛物线的解析式；
(2)如图1，E为△ABC边AB上的一动点，F为BC边上的一动点，D点坐标为0,−2，
①求DE+EF的最小值②求△DEF周长的最小值；
(3)如图2，N为射线CB上的一点，M是地物线上的一点，M、N均在第一象限内，B、N位于直线AM的同侧，且AM∥CN，当△AMN为等腰三角形时，求点N的坐标．（直接写出点N的坐标，不要求写解答过程）
【答案】(1)y=x2−2x−3
(2)①522，②26
(3)(72，12)或(1+21，−2+21)或(6+21，3+21)．
【分析】（1）利用待定系数法把问题转化为方程组解决；
（2）①设D1为D关于直线AB的对称点，连接D1E，EF，根据点到直线的距离垂线段最短可知，当D1、E、F三点共线，而且D1F⊥BC时，ED+EF=D1E+EF最小，最小值为D1F，②设D1为D关于直线AB的对称点，D2为D关于直线BC的对称点，连接D1E，D2F，D1D2．当D1，E．F．D2共线时，△DEF的周长最小，最小值为D1D2的长；
（3）求出直线AM的解析式，利用方程组求出点M的坐标，过点M作x轴的平行线l，过点N作y轴的平行线交x轴于点P，交直线l于点Q．分三种情形：当AM=AN时，当AM=MN时，当AN=MN时，分别构建方程求解．
【详解】（1）解：∵抛物线y=x2+bx+c经过点A(−1,0)，点C(0,−3)．
∴ 1−b+c=0c=−3，
∴ b=−2c=−3，
∴抛物线的解析式为y=x2−2x−3；
（2）令y=0，则x2−2x−3=0，
解得x=−1或3，
∴B(3,0)，
∴OB=OC=3，
∴△BOC是等腰直角三角形，∠OCB=45°
①设D1为D关于直线AB的对称点，连接D1E，EF，

∴ED+EF=D1E+EF，
根据点到直线的距离垂线段最短可知，当D1、E、F三点共线，而且D1F⊥BC时，ED+EF=D1E+EF最小，最小值为D1F，
如图1，过D1点作D1F⊥BC，垂足为F，
此时△FCD1是等腰直角三角形， D1F=22CD1=22×[2−(−3)]=522，
故DE+EF的最小值为522；
②如解图2，设D1为D关于直线AB的对称点，D2为D关于直线BC的对称点，连接D1E，D2F，D1D2．

由对称性可知DE=D1E，DF=D2F，△DEF的周长=D1E+EF+D2F，
∴当D1，E．F．D2共线时，△DEF的周长最小，最小值为D1D2的长，
令y=0，则x2−2x−3=0，
解得x=−1或3，
∴B(3,0)，
∴OB=OC=3，
∴△BOC是等腰直角三角形，∠OCB=45°
∵BC垂直平分DD2，且∠OCB=∠D2CB=45°，D(0,−2)，
∴CD=CD2=1，∠OCD2=90°
∴D2(1,−3)，
∵D，D1关于x轴对称，
∴D1(0,2)，
∴D1D2=D2C2+D1C2=52+12=26，
∴△DEF的周长的最小值为26．
（3）设直线BC的解析式为y=kx+m，
则有m=−33k+m=0，
∴ k=1m=−3，
∴直线BC的解析式为y=x−3，
∴设直线AM的解析式为y=x+n，
∵A(−1,0)，
∴直线AM的解析式为y=x+1，
由y=x+1y=x2−2x−3，解得x=−1y=0或x=4y=5，
∴M(4,5)，
∵点N在射线CB上，
∴设N(t,t−3)，
过点M作x轴的平行线l，过点N作y轴的平行线交x轴于点P，交直线l于点Q．

∵A(−1,0)，M(4,5)，N(t,t−3)，
∴AM=52，AN=(t+1)2+(t−3)2，MN=(t−4)2+(t−8)2，
∵△AMN是等腰三角形，
当AM=AN时，52=(t+1)2+(t−3)2，解得t=1±21，
当AM=MN时，52=(t−4)2+(t−8)2，解得t=6±21，
当AN=MN时，(t+1)2+(t−3)2=(t−4)2+(t−8)2，解得t=72，
∵N在第一象限，
∴t>3，
∴t的值为72，1+21，6+21，
∴点N的坐标为(72，12)或(1+21，−2+21)或(6+21，3+21)．
【点睛】本题属于二次函数综合题，考查了二次函数的性质，一次函数的性质，轴对称最短问题，等腰三角形的判定和性质等知识，解题的关键是学会利用轴对称解决最短问题，学会用分类讨论的思想思考问题，属于中考压轴题．
【题型4 面积的最值问题】
【例4】（23-24九年级·云南红河·期中）如图，抛物线y=ax2+bx−4与x轴交于A−3，0、B4，0两点，与y轴交于点C．
(1)求抛物线解析式；
(2)点H是抛物线对称轴上的一个动点，连接AH、CH，求出△ACH周长的最小值时点H的坐标；
(3)若点G是第四象限抛物线上的动点，求△BCG面积的最大值以及此时点G的坐标；
【答案】(1)y=13x2−13x−4
(2)H12,−3.5
(3)△BCG面积的最大值为83，此时G2,−103
【分析】（1）利用待定系数法确定二次函数解析式即可；
（2）将抛物线解析式变形为顶点式，然后确定出抛物线的对称轴，连接BC交对称轴于点H，则点H即为所求，求得直线BC的解析式，令x=12，即可求解；
（3）设Gt，13t2−13t−4，(0【详解】（1）解：∵抛物线y=ax2+bx−4与x轴交于A−3，0、B4，0两点，
∴9a−3b−4=016a+4b−4=0，
解得：a=13b=−13，
∴抛物线的解析式为：y=13x2−13x−4；
（2）y=13x2−13x−4=13x−122−4912，
∴抛物线的对称轴为x=12，
当x=0时，y=−4，
如图所示：连接BC交对称轴于点H，则△ACH周长的最小；
∵A−3，0、B4，0两点关于x=12对称，
∴抛物线的对称轴为直线x=12
当x=0时，y=−4，
∴C(0,−4)
∵B4，0，C(0,−4)，
设直线BC的解析式为y=kx−4，
则4k−4=0，解得：k=1，
∴直线BC的解析式为y=x−4，
当x=12时，y=−3.5
∴H12,−3.5
（3）如图2所示：设Gt，13t2−13t−4，(0过点G作GF∥y轴，交BC于点F，
设直线BC的解析式为y=kx+d，
∵B4,0，C0,−4，
∴4k+d=0d=−4，
解得：k=1d=−4，
直线BC的解析式为：y=x−4，
∴Ft,t−4，
∴FG=t−4−13t2−13t−4=−13t2+43t，
∴S△BCG=S△BFG+S△CFG
=12FG·4−t+12FG·t−0
=2−13t2+43t
=−23t−22+83
∵−23<0，
∴当t=2时，y=−103，△BCG面积的最大值为83，此时G2,−103．
【点睛】题目主要考查二次函数与一次函数的综合问题，包括待定系数法确定函数解析式，最短周长及最大面积问题，理解题意，熟练掌握二次函数的应用是解题关键．
【变式4-1】（23-24九年级·甘肃武威·阶段练习）如图，抛物线y=ax2+bx+c与x轴交于点A−2,0和点B4,0，与y轴交于点C0,4．
(1)求抛物线的解析式．
(2)点D在抛物线的对称轴上，当AD+CD取得最小值时，求此时点D的坐标．
(3)点P是直线BC上方抛物线上一动点，连接CP、BP，求△PBC的面积的最大值，并求此时点P的坐标．
【答案】(1)y=−12x2+x+4
(2)D1，3
(3)4；P2，4
【分析】（1）利用待定系数法可求解析式；
（2） 根据A，B是对称点，连接BC，交对称轴于点D，利用直线解析式与对称轴交点坐标计算即可．
（3）由待定系数法求出直线BC的解析式，过点P作y轴的平行线，交BC于Q，设Pm，−12m2+m+4，则Qm，−m+4，则PQ=−12m2+2m，表示出S△PCB=−m−22+4，根据二次函数的性质即可得到答案．本题考查了待定系数法，抛物线的最值，线段和最小，熟练掌握抛物线的最值是解题的关键．
【详解】（1）∵抛物线y=ax2+bx+c过点A(−2,0),B(4,0),C(0,4)
设抛物线解析式为y=ax−4x+2，
故4=a0−40+2，
解得a=−12，
故抛物线的解析式为y=−12x−4x+2=−12x2+x+4．
（2）∵抛物线y=−12x−4x+2=−12x−12+92，
∴对称轴为直线x=1，
设直线BC的解析式为：y=kx+b，
将B4，0，C0，4代入直线BC的解析式得：
解得k=−1b=4，
∴直线BC的解析式为：y=−x+4，
∵A，B是对称点，连接BC，交对称轴于点D，此时AD+CD取得最小值，
当x=1时，
y=−x+4=3，
故D1，3．
（3）如图，过点P作y轴的平行线，交BC于Q，
设Pm，−12m2+m+4，则Qm，−m+4，
则PQ=−12m2+2m，，
∴S△PCB=S△PCQ+S△BPQ
=12PQxP−xC+12PQxB−xP
=12PQxP−xC+xB−xP
=12PQxP−xC+xB−xP
=12PQxB−xC
=12PQ×4−0
=2PQ=−m2+4m
=−m2−4m
=−m−22+4，由此可得，
当m=2，S△BCP最大为4，
当m=2时，−12m2+m+4=4，
∴P2，4．
【变式4-2】（23-24九年级·山东·期末）如图所示，抛物线与x轴交于A、B两点，与y轴交于点C，且OA=1，OB=OC=4．

(1)求抛物线的解析式；
(2)若连接AC、BC．动点D从点A出发，在线段AB上以每秒1个单位长度向点B做匀速运动；同时，动点E从点B出发，在线段BC上以每秒2个单位长度向点C做匀速运动，当其中一点到达终点时，另一点随之停止运动，连接DE，设运动时间为t秒．在D、E运动的过程中，当t为何值时，四边形ADEC的面积最小，最小值为多少？
(3)点M是抛物线上位于x轴上方的一点，点N在x轴上，是否存在以点M为直角顶点的等腰直角三角形CMN？若存在，求出点M的坐标，若不存在，请说明理由．
【答案】(1)y=−x2+3x+4
(2)t=52时，四边形ADEC的面积最小，最小值为558
(3)存在，M1+5,1+5或M2−22,22−2
【分析】（1）根据交点式列出函数解析式，即可求解；
（2）根据题意可得△OBC是等腰直角三角形，过点E作EF⊥x轴，垂足为F，根据SADEC=S△ABC−S△BDE列出函数关系式，进而根据二次函数的性质，即可求解；
（3）过点M作y轴的平行线PQ，交x轴于点Q，过点C作CP⊥PQ，设M(m,−m2+3m+4)，证明△CPM≌△MQN，可得CP=MQ，进而列出方程，解方程即可求解；
【详解】（1）解：∵OB=OC=4，OA=1，则C0,4，B4,0，A0,−1
∴抛物线解析式为y=−(x+1)(x−4)=−x2+3x+4；
（2）解：∵OB=OC=4，
∴△OBC是等腰直角三角形，由点的运动可知：
BE=2t，过点E作EF⊥x轴，垂足为F，

∴BF=EF=2t2=t，
又∵A0,−1，则AB=5，
∴SADEC=S△ABC−S△BDE
=12×4×5−12×(5−t)×t
=12(t−52)2+558，
∵当其中一点到达终点时，另一点随之停止运动，
∴AC=42+42=42，AB=5，
∴0≤t≤4，
当t=52时，四边形ADEC的面积最小，即为558；
（3）解：存在，M(1+5,1+5)或M(2−22,22−2)，
当点M在CN的右侧时，如图所示，

过点M作y轴的平行线PQ，交x轴于点Q，过点C作CP⊥PQ，
∵△CMN是以M为直角为直角顶点的等腰直角三角形，
∴CM=MN，∠CMN=90°，
∴∠PCM=90°−∠PMC=∠NMQ，
又∠CPM=∠MQN=90°
∴△CPM≌△MQN，
∴CP=MQ，
设M(m,−m2+3m+4)，
∴−m2+3m+4=m，
解得：m=5+1或m=1−5（舍去）
∴M(1+5,1+5)；
当点M在CN的右侧时，同理可得−m2+3m+4=−m，
解得：m=2−22或m=22+2（舍去）
∴M(2−22,22−2)，
综上所述，M(1+5,1+5)或M(2−22,22−2)．
【点睛】本题考查二次函数的综合运用，解题的关键是求出解析式，分类讨论点根据面积加减及线段关系列式求解．
【变式4-3】（23-24九年级·福建福州·期中）已知抛物线y=ax2+bx+ca≠0与y轴交于点A0,−5，顶点为B2,−1，过点C2,−5直线与抛物线交于D，E两点（点D在点E的左侧）．
(1)求抛物线的解析式；
(2)求△BDE面积的最小值；
(3)若D，E两点都在第四象限，过点D作直线y=−1的垂线，垂足为F，直线EB与直线DF交于点G，连接CF，求证：四边形BCFG是平行四边形．
【答案】(1)y=−x2+4x−5
(2)8
(3)见解析
【分析】（1）由抛物线的顶点为B2,−1，设y=ax−22−1，将A0,−5代入即可求解；
（2）设过点C2,−5的直线为y=kx+b，将C2,−5代入可求得y=kx+−5−2k，联立抛物线可得：kx+−5−2k=−x2+4x−5，整理得：x2+k−4x−2k=0，可知xD+xE=−k−4，xD⋅xE=−2k，由题意可得S△BDE=12BC⋅xB−xD+12BC⋅xE−xB=12BC⋅xE−xD=2xE−xD，要使得S△BDE最小，即xE−xD最小即可，再根据xE−xD=xD+xE2−4xDxE即可求解；
（3）由题意可知DG∥BC，xD=xG，FxD,−1，由（2）可知xD，xE为方程x2+k−4x−2k=0的解，可得xD−2=−k−k2+162，xE−2=−k+k2+162，设直线BE为y=mx+n，将B2,−1，ExE,yE，代入可求得m=k−4xE−2n=−1−2m，当x=xD时，y=mxD+n，可得点G的纵坐标yG=mxD−1−2m=mxD−2−1，进而可得FG=yG−yF=mxD−2=k−4xE−2xD−2，化简可得BC=FG=4，进而可证明四边形BCFG是平行四边形．
【详解】（1）解：∵抛物线的顶点为B2,−1，
∴y=ax−22−1，
将A0,−5代入y=ax−22−1，可得：−5=4a−1，
解得：a=−1，
∴抛物线的解析式为：y=−x−22−1=−x2+4x−5；
（2）设过点C2,−5的直线为y=kx+b，
将C2,−5代入可得：−5=2k+b，即：b=−5−2k，
∴y=kx+−5−2k，
联立抛物线可得：kx+−5−2k=−x2+4x−5，
整理得：x2+k−4x−2k=0，
点D，点E为直线y=kx+b与y=−x2+4x−5的交点，则方程x2+k−4x−2k=0的解为两点的横坐标，xD∴xD+xE=−k−4，xD⋅xE=−2k，
∵B2,−1，C2,−5，
∴BC∥y轴，BC=4
则S△BDE=12BC⋅xB−xD+12BC⋅xE−xB=12BC⋅xE−xD=2xE−xD，
要使得S△BDE最小，即xE−xD最小即可，
xE−xD=xD+xE2−4xDxE
=−k−42−4×−2k
=k2+16，
∵k2+16≥16，
∴xE−xD≥16=4，
∴S△BDE的最小值为：2×4=8，
即：△BDE面积的最小值为8．
（3）证明：∵B2,−1，则点B在直线y=−1上，
则，由题意可知：DF⊥BF，则FxD,−1，
∵BC∥y轴，则BC⊥BF，
∴DG∥BC，则xD=xG，
由（2）可知xD，xE为方程x2+k−4x−2k=0的解，
∴xD=−k+4−k2+162，xE=−k+4+k2+162，
则xD−2=−k−k2+162，xE−2=−k+k2+162，
yE=kxE+−5−2k=kxE−2−5，
设直线BE为y=mx+n，将B2,−1，ExE,yE，代入可得−1=2m+nyE=xEm+n，即m=yE+1xE−2=kxE−2−5+1xE−2=k−4xE−2n=−1−2m，
∴当x=xD时，y=mxD+n，
即：点G的纵坐标yG=mxD−1−2m=mxD−2−1，
∴FG=yG−yF=mxD−2−1−−1=mxD−2，
即：FG=mxD−2
=k−4xE−2xD−2
=k−4−k+k2+162⋅−k−k2+162
=k−8−k+k2+16⋅−k−k2+162
=−kk2+16+k2+4k2+16+4kk2+16−k
=−kk2+16+kk2+16−k2k2+16−k+8k2+16+8k2k2+16−k
=−kk2+16−k22k2+16−k+8k2+16+8k2k2+16−k
=8k2+16+8k−16k2k2+16−k
=8k2+16−k2k2+16−k
=4，
则BC=FG=4，
又∵DG∥BC，
∴四边形BCFG是平行四边形．
【点睛】本题考查待定系数法求函数解析式，平行四边形的判定，一元二次方程根与系数的关系，利用参数表示点的坐标是解决问题的关键．
【题型5 线段和差倍分的最值】
【例5】（23-24·山东济南·一模）抛物线y=−12x2+a−1x+2a与x轴交于Ab,0，B4,0两点，与y轴交于点C0,c，点P是抛物线在第一象限内的一个动点，且在对称轴右侧．
(1)求a，b，c的值；
(2)如图1，连接BC、AP，交点为M，连接PB，若S△PMBS△AMB=14，求点P的坐标；
(3)如图2，在（2）的条件下，过点P作x轴的垂线交x轴于点E，将线段OE绕点O逆时针旋转得到OE'，旋转角为α(0°<α<90°)，连接E'B，E'C，求E'B+34E'C的最小值．
【答案】(1)a=2，b=−2，c=4
(2)P3,52
(3)3374
【分析】（1）利用待定系数法求解即可；
（2）过点P作PD⊥x轴，交BC于点D，过点A作y轴的平行线交BC的延长线于H，求得lBC的解析式，设Pm,−12m2+m+4，则Dm,−m+4，利用相似三角形的判定与性质可得答案；
（3）在y轴上取一点F，使得OF=94，连接BF，由相似三角形的判定与性质可得FE'=34CE'，可得E'B+34E'C=BE'+E'F，即可解答．
【详解】（1）解：将B4,0代入y=−12x2+a−1x+2a，
得−8+4a−1+2a=0，
∴a=2，
∴抛物线的解析式为y=−12x2+x+4，
令x=0，则y=4，
∴c=4，
令y=0，则0=−12x2+x+4，
∴x1=4，x2=−2，
∴A−2,0，即b=−2；
∴a=2，b=−2，c=4
（2）过点P作PD⊥x轴，交BC于点D，过点A作y轴的平行线交BC的延长线于H，

设lBC：y=kx+b，将0,4，4,0代入得b=44k+b=0解得：b=4，k=−1，
∴lBC：y=−x+4，
设Pm,−12m2+m+4，则Dm,−m+4，
PD=yP−yD=−12m2+m+4−−m+4=−12m2+2m，
∵PD∥HA，
∴△AMH∽△PMD，
∴PMMA=PDHA，
将x=−2代入y=−x+4，
∴HA=6，
∵S△PMBS△AMB=12PM⋅ℎ12AM⋅ℎ=PMAM=14，
∴PDHA=PD6=14，
∴PD=32，
∴32=−12m2+2m，
∴m1=1(舍)，m2=3，
∴P3,52；
（3）在y轴上取一点F，使得OF=94，连接BF，

根据旋转得性质得出：OE'=OE=3，
∵OF⋅OC=94×4=9，
∴OE'2=OF⋅OC，
∴ OE'OF=OCOE'，
∵ ∠COE'=∠FOE'，
∴ △FOE'∽△E'OC，
∴ FE'CE'=OE'OC=34，
∴ FE'=34CE'，
∴ E'B+34E'C=BE'+E'F，当B、E'、F三点共线时，此时E'B+34E'C最小=BF，
最小值为：BF=42+942=3374．
【点睛】此题考查的是二次函数的综合题意，涉及到相似三角形的判定与性质、二次函数与面积的问题、待定系数法求解析式，旋转的性质等知识．正确的作出辅助线是解此题的关键．
【变式5-1】（23-24九年级·安徽合肥·阶段练习）如图，在平面直角坐标系中，抛物线y=−x2+23x的顶点为A点，且与x轴的正半轴交于点B．

（1）连接AO，AB，则△AOB为 三角形；
（2）P点为该抛物线对称轴上一点，当OP+12AP取最小值时，OP= ．
【答案】 等边 2
【分析】连接AO、AB，PB，作PH⊥OA于H，BC⊥AO于C，解方程得到−x2+23x=0得B(23，0)，利用配方法得到A(3，3)，则OA=23，从而可判断△AOB为等边三角形，接着利用∠OAP=30°得到PH=12AP，利用抛物线的对称性得到PO=PB，所以OP+12AP=PB+PH，根据两点之间线段最短得到当H、P、B共线时，PB+PH的值最小，最小值为BC的长，然后计算出BC的长，继而求出OC，再利用勾股定理和含30度的直角三角形的性质求出OP'即可．
【详解】解：连接PB，作PH⊥OA于H，BC⊥AO于C，如图，
当y=0时，−x2+23x=0，
解得x1=0，x2=23，则B(23，0)，
y=−x2+23x=−(x−3)2+3，则A(3，3)，
∴OA=(3)2+32=23，
而AB=AO=23，
∴AB=AO=OB，
∴△AOB为等边三角形，
∴∠OAP=30°，
∴PH=12AP，
∵AP垂直平分OB，
∴PO=PB，
∴OP+12AP=PB+PH，
当H、P、B共线时，PB+PH的值最小，最小值为BC的长，
而BC=32AB=32×23=3，
则OC=OB2−BC2=3=12OB，此时OP'=P'B，
∴∠OBC=∠P'OB=30°，
∴∠AOP'=30°，
∴OP'=OC3×2=2，
故答案为：等边；2．

【点睛】本题考查了抛物线与x轴的交点，勾股定理，等边三角形的判定和性质，含30度的直角三角形的性质，把求二次函数y=ax2+bx+c(a，b，c是常数，a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程．也考查了二次函数的性质和最短路径的解决方法．
【变式5-2】 （23-24九年级·安徽阜阳·阶段练习）已知抛物线与x轴相交于A，B两点，与y轴相交于点C0，6，顶点为D2，8．

(1)求此抛物线的解析式；
(2)如图1，点P为抛物线对称轴（直线l）上的动点，求当PB−PC取得最小值时点P的坐标；
(3)如图2，在第一象限内，抛物线上有一动点M，求△BCM面积的最大值．
【答案】(1)y=−12x2+2x+6；
(2)点P的坐标为2，2；
(3)△BCM面积的最大值为272．
【分析】（1）设出顶点式，利用待定系数法即可求解；
（2）先求得A，B两点的坐标，当PB=PC时，PB−PC取得最小值，利用两点之间的距离公式列式求解即可；
（3）连接OM，设Mm，−12m2+2m+6，利用S△BCM=S△BOM+S△COM−S△BOC列式得S△BCM=−32m−32+272，利用二次函数的性质即可求解．
【详解】（1）解：设抛物线的解析式为y=ax−22+8，
∵经过点C0，6，
∴6=a0−22+8，
解得a=−12，
∴抛物线的解析式为y=−12x−22+8=−12x2+2x+6；
（2）解：令y=0，则−12x−22+8=0，
解得x=−2或x=6，
∴A−2，0，B6，0，
设点P的坐标为2，n，
当PB=PC时，PB−PC=0，
当PB≠PC时，PB−PC>0，
∴当PB=PC时，PB−PC取得最小值，
此时PB2=PC2，即2−62+n−02=2−02+n−62，
解得n=2，
∴点P的坐标为2，2；
（3）解：连接OM，如图，

设Mm，−12m2+2m+6 0∴S△BCM=S△BOM+S△COM−S△BOC
=12×6−12m2+2m+6+12×6m−12×6×6
=−32m2+9m
=−32m−32+272，
∵−32<0，
∴△BCM面积的最大值为272．
【点睛】本题考查了利用待定系数法求二次函数的解析式，二次函数的图象及性质，熟练掌握二次函数的图象及性质是解题的关键．
【变式5-3】（23-24九年级·广东东莞·期中）如图，已知抛物线y=ax2+bx+c（a≠0）与y轴相交于点C0,−2，与x轴分别交于点B3,0和点A，且∠CAO=45°．
(1)求抛物线解析式；
(2)抛物线上是否存在一点Q，使得∠BAQ=∠ABC，若存在，请求出点Q坐标，若不存在，请说明理由；
(3)抛物线的对称轴交x轴于点D，在y轴上是否存在一个点P，使22PC+PD的值最小，若存在，请求出最小值，若不存在，请说明理由．
【答案】(1)y=13x2−13x−2
(2)存在，点Q坐标为5,143或(1,−2)
(3)存在，524
【分析】（1）根据点C的坐标，∠CAO=45°可求出点A的坐标，运用待定系数法即可求解；
（2）如图所示，过点A作AM∥BC交y轴于点M，交抛物线于点Q，作M关于x轴的对称点M'，作AM'交抛物线于Q'，根据题意分别计算出直线AM,AQ'的解析式，根据直线与抛物线由交点，联立方程组求解即可；
（3）如图所示，过点P作PH⊥AC于H，过点D作DH'⊥AC于H'，交y轴于点P'，根据点A,C的坐标可得△AOC是等腰直角三角形，由此可得△PHC,△DH'C是等腰直角三角形，可得22PC=PH，当P运动到P'，H和H'重合时，22PC+PD的值最小，最小值是DH'，根据抛物线的特点可得点D的坐标，由此可求出AD的长，根据等腰直角三角形的性质即可求解．
【详解】（1）解：∵C(0,−2)，
∴OC=2，
∵∠CAO=45°，
∴OC=OA，
∴OA=2，
∴A(−2,0)，
将A(−2,0)，B(3，0)，C(0,−2)代入y=ax2+bx+ca≠0得，
4a−2b+c=09a+3b+c=0c=−2，解得，a=13b=−13c=−2，
∴抛物线的解析式为：y=13x2−13x−2．
（2）解：存在一点Q，使得∠BAQ=∠ABC，理由如下：
如图所示，过点A作AM∥BC交y轴于点M，交抛物线于点Q，作M关于x轴的对称点M'，作AM'交抛物线于Q'，
∵AM∥BC，
∴∠QAB=∠ABC，即点Q是满足题意的点，
∵B(3，0)，C(0,−2)，
∴直线BC的解析式为：y=23x−2，
设直线AM的解析式为：y=23x+m，将A(−2,0)代入得：0=23×−2+m，
∴m=43，
∴直线AM的解析式为：y=23x+43，M0,43，
直线AM与抛物线联立方程组得y=23x+43y=13x2−13x−2，
解得，x=−2y=0（与A重合，舍去）或x=5y=143，
∴Q5,143，
∵M、M'关于x轴对称，
∴直线BC的解析式为：y=23x−2，
∴∠Q'AB=∠QAB=∠ABC，M'0,−43，
∴Q'是满足题意的点，
设直线AQ'的解析式为：y=kx−43，将A(−2,0)代入得：−2k−43=0，
∴k=−23，
∴直线AQ'的解析式为：y=−23x−43，
直线AQ'与抛物线联立方程组得y=−23x−43y=13x2−13x−2，
解得，x=−2y=0（与A重合，舍去）或x=1y=−2，
∴Q(1,−2)，
综上所述，点Q坐标为5,143或(1,−2)．
（3）解：在y轴上存在一个点P，使22PC+PD的值最小，理由如下：
如图所示，过点P作PH⊥AC于H，过点D作DH'⊥AC于H'，交y轴于点P'，
∵y=13x2−13x−2=13x−122−2512，
∴抛物线的对称轴为直线x=12，
∴D12,0，
∵A(−2,0)，C(0,−2)，则OA=OC=2，
∴△AOC是等腰直角三角形
∴∠OCA=45°=∠OAC，
∴△PCH是等腰直角三角形，
∴PH=22PC，
∴22PC+PD最小即是PH+PD最小，
∴当P运动到P'，H和H'重合时，22PC+PD的值最小，最小值是DH'，
∵∠OAC=45°，DH'⊥AC，
∴△ADH'是等腰直角三角形，
∴DH'=22AD，
∵A(−2,0)，D12,0，
∴AD=52，
∴DH'=524，即22PC+PD的最小值为524．
【点睛】本题主要考查二次函数与几何图形的综合，掌握待定系数法解二次函数解析式，几何图形的变换特点，一次函数与二次函数联立方程组求解，等腰直角三角形的判定和性质等知识的综合运用是解题的关键．
【题型6 由二次函数性质求二次函数的最值】
【例6】（23-24九年级·陕西西安·阶段练习）如图，抛物线y=ax2+bx+3与x轴交于点A1,0,B3,0，与y轴交于点C．

(1)求抛物线的解析式；
(2)点Mx1,y1,Nx2,y2是抛物线上不同的两点且x1+x2=4x1−x2，求y1−y2的最小值．
【答案】(1)y=x2−4x+3
(2)y1−y2的最小值为−1
【分析】（1）抛物线y=ax2+bx+3与x轴交于点A1,0,B3,0，可设y=ax−1x−3，求出点C的坐标，代入函数解析式求出a的值，即可得到答案；
（2）根据题意得到y1−y2=4x1−x2−122−1，进一步即可得到y1−y2的最小值．
【详解】（1）解：设抛物线的表达式为y=ax−1x−3，
∵图象与y轴交于点C，当x=0时，y=ax2+bx+3=3，
∴C0,3，
代入y=ax−1x−3得，
∴3a=3，
解得，a=1，
∴抛物线的解析式为y=x−1x−3，
即y=x2−4x+3；
（2）∵y1−y2=x12−4x1+3−x22−4x2+3
=x1+x2x1−x2−4x1−x2，x1+x2=4x1−x1，
∴y1−y2=4x1−x22−4x1−x2=4x1−x2−122−1，
∵4x1−x2−122≥0，
∴4x1−x2−122−1≥−1，
∴y1−y2的最小值为−1．
【点睛】此题考查了待定系数法求二次函数解析式、二次函数的图象和性质等知识，读懂题意和准确计算是解题的关键．
【变式6-1】（23-24九年级·江西赣州·期中）观察下列两个数的乘积，说明其中哪个积最大．
1×100,2×99,3×98,4×97,⋅⋅⋅,99×2,100×1．
【观察发现】（1）发现所列各组式子中两个因数的和都为_____________．
【问题解决】（2）若设其中一个因数为x（1≤x≤100，且为正整数），所列两个数的积为y，请说明哪个积最大，最大值是多少．
【拓展应用】（3）若大于0的a、b满足a+b=4，求a2+b2的最小值．
【答案】（1）101；（2）x取50或51时，y最大为2250；（3）8
【分析】（1）两因数相加即可；
（2）可将题目中的算式设为y=x101−x的形式，利用二次函数的最值求得结果；
（3）由题意可知b=4−a，a2+b2=a2+(4−a)2，再次利用二次函数的最值求得结果即可.
【详解】（1）1+100=2+99=3+98=4+97=⋯=99+2=100+1=101，
故答案为：101；
（2）由题意可知，另一个因数为101−x,
则y=x101−x=−x2+101x（1≤x≤100，且为正整数），
对称轴为x=−b2a=1012，因x是正整数，且1≤x≤100，
所以x取50或51时，y最大为2250．
（3）∵a+b=4,∴b=4−a，
∴a2+b2=a2+(4−a)2=2a2−8a+16=2(a−2)2+8，
当x=2时，有最小值为8．
【点睛】本题主要考查了根据已知归纳规律和二次函数的最值问题，发现规律，运用二次函数的最值证明是解答此题的关键.
【变式6-2】（（23-24·贵州·模拟预测）已知二次函数y=ax2−4x+c（a≠0，a，c为常数）的图象经过点1,−6，−4,−1
(1)求二次函数的表达式；
(2)当−1≤x＜0时，求二次函数的最大值；
(3)当m≤x≤0时，二次函数的最大值与最小值的和为2m，求m的值．
【答案】(1)y=−x2−4x−1；
(2)最大值为2；
(3)m=−3+7或−3−11
【分析】本题考查了待定系数法求二次函数解析式、二次函数的图象与性质，熟练掌握二次函数的性质是解此题的关键．
（1）利用待定系数法计算即可得出答案；
（2）先求出抛物线的顶点坐标为−2,3，再根据抛物线的性质得出当x=−1时，y有最大值为2；
（3）由（2）得：抛物线的对称轴为直线x=−2，再分两种情况：当−2≤m<0时，当m<−2时，分别计算即可得出答案．
【详解】（1）解：把1,−6，−4,−1代入y=ax2−4x+c，得：a−4+c=−616a+16+c=−1，
解得：a=−1c=−1，
∴二次函数的表达式为y=−x2−4x−1；
（2）解：∵y=−x2−4x−1=−x+22+3，
∴抛物线的顶点坐标为−2,3，
∵−1<0，
∴抛物线开口向下，
又∵−1≤x≤0，
∴当x=−1时，y有最大值为2；
（3）解：由（2）得：抛物线的对称轴为直线x=−2，
∴当x>−2时，y随x的增大而减小；
当x<−2时，y随x的增大而增大，
①当−2≤m<0时，
当x=0时，y有最小值为−1，
当x=m时，y有最大值为−m2−4m−1，
∴−m2−4m−1+−1=2m，
∴m=−3+7或m=−3−7（舍去）．
②当m<−2时，
当x=−2时，y有最大值为3，
∵y的最大值与最小值之和为2m，
∴y最小值为2m−3，
∴−m+22+3=2m−3，
∴m=−3−11或m=−3+11（舍去）．
综上所述，m=−3+7或−3−11．
【变式6-3】（23-24九年级·湖南长沙·开学考试）在平面直角坐标系中，我们将形如1,−1，−2.1,2.1这样，纵坐标与横坐标互为相反数的点称之为“互补点”．
(1)直线y=2x−3上的“互补点”的坐标为_________；
(2)直线y=kx+2k≠0上是否有“互补点”，若有，请求出点的坐标，若没有请说明理由；
(3)若函数y=14x2+n−k−1x+m+k−2的图象上存在唯一的一个“互补点”，且当−1≤n≤2时，m的最小值为k，求k的值．
【答案】(1)1,−1
(2)直线y=kx+2k≠0上有“互补点”，点的坐标为−2k+1,2k+1k≠0，k≠−1
(3)1或3+3
【分析】（1）设直线y=2x−3上的“互补点”的坐标为x,2x−3，则可得出−x=2x−3，解出x的值，即可得出答案；
（2）设直线y=kx+2k≠0上存在“互补点”t,−t，则可得−t=kt+2，解出t的值，即可得出答案；
（3）设“互补点”的坐标为a,−a，则方程−a=14a2+n−k−1a+m+k−2有唯一解，则其根的判别式Δ=0，即16n−k2−4×4m+k−2=0，m=n−k2−k+2．再结合二次函数的性质分类讨论①当−1≤k≤2时， ②当k<−1时和③当k>2时求解即可．
【详解】（1）设直线y=2x−3上的“互补点”的坐标为x,2x−3，
∴−x=2x−3，
解得：x=1，
∴直线y=2x−3上的“互补点”的坐标为1,−1，
故答案为：1,−1；
（2）设直线y=kx+2k≠0上存在“互补点”t,−t，
则由题意得：−t=kt+2，
解得：t=−2k+1k≠0,k≠−1，
∴直线y=kx+2k≠0上有“互补点”，点的坐标为−2k+1,2k+1k≠0，k≠−1；
（3）设“互补点”的坐标为a,−a，
由题意可知，方程−a=14a2+n−k−1a+m+k−2有唯一解，
整理得：a2+4n−ka+4m+k−2=0，
∴Δ=16n−k2−4×4m+k−2=0．
整理得：m=n2−2kn+k2−k+2=n−k2−k+2．
∴当nk时，m随n的增大而增大；当n=k时，m取得最小函数值−k+2．
①当−1≤k≤2时，此时当n=k时，m取得最小值，
由题意得−k+2=k，解得k=1；
②当k<−1时，此时当n=−1时，m取得最小值，
由题意得−1−k2−k+2=k，
整理得：k2+2=0，方程无解；
③当k>2时，此时当n=2时，m取得最小值，
由题意得2−k2−k+2=k，
整理得：k2−6k+6=0，
解得k1=3+3，k2=3−3（舍）．
综上所述，k的值为1或3+3．
【点睛】本题考查一次函数的图象和性质，二次函数的图象和性质．读懂题意，理解“互补点”的定义是解题关键．
【题型7 由二次函数的最值求字母的值】
【例7】（（23-24九年级·全国·专题练习）已知在平面直角坐标系中，设二次函数y1=x2+bx+a，y2=ax2+bx+1(a、b是实数，a≠0)．
(1)若函数y1的对称轴为直线x=3，且函数y1的图象经过点(a,−6)，求函数y1的表达式；
(2)若函数y1的图象经过点(r,0)，其中r≠0，求证：函数y2的图象经过点(1r，0)；
(3)设函数y1和函数y2的最小值分别为m和n，若m+n=0，求m、n的值．
【答案】(1)y1=x2−6x+2或y1=x2−6x+3
(2)证明见解析
(3)m=0，n=0
【分析】（1）由对称轴可得b=−6，再将点(a,−6)代入y1=x2−6x+a即可求a的值，进而求函数解析式；
（2）将点(r,0)代入y1，得到0=r2+br+a，再方程两边同时除以r2，1r是ax2+bx+1=0的解，即可证明函数y2的图象经过点(1r，0)；
（3）分别求出m=a−b24，n=1−b24a，由题意可得a>0，且(a+1)(4a−b2)=0，即可得b2=4a，从而求出m=n=0．
本题考查二次函数图象上点的坐标特点，熟练掌握二次函数对称轴、最大（小)值的求法是解题的关键．
【详解】解：（1）∵函数y1的对称轴为直线x=3，
∴−b2=3，
∴b=−6，
∴y1=x2−6x+a，
∵函数y1的图象经过点(a,−6)，
∴−6=a2−6a+a，
∴a2−5a+6=0，
解得a=2或a=3，
∴y1=x2−6x+2或y1=x2−6x+3；
（2）∵函数y1的图象经过点(r,0)，
∴0=r2+br+a，
∵r≠0，
方程两边同时除以r2得，1+br+1r2a=0，
即a(1r)2+b⋅1r+1=0，
∴ 1r是ax2+bx+1=0的解，
∴函数y2的图象经过点(1r，0)；
（3）∵函数y1和函数y2的最小值分别为m和n，
∴m=a−b24，n=1−b24a，
∵m+n=0，
∴a−b24+1−b24a=0，
∴(a+1)(4a−b2)=0，
∴b2=4a或a=−1，
∵函数y1和函数y2都有最小值，
∴a>0，
当b2=4a时，m=0，n=0．
【变式7-1】（23-24九年级·河南许昌·期末）如图，已知二次函数y=x2+ax+a−4的图象经过点P−2,−2．
(1)求a的值和二次函数图象的顶点坐标．
(2)已知点Qm,n在该二次函数图象上．
①当m=−3时，求n的值；
②当m≤x≤m+1时，该二次函数有最小值1，请结合函数图像求出m的值．
【答案】(1)a=2，−1,−3
(2)①当m=−3时，n=1；②m=−4或m=1
【分析】本题考查二次函数的图象、性质、最值等；
（1）将点P−2,−2代入二次函数，利用待定系数法求解a的值；将该二次函数的解析式配方，可得图象的顶点坐标；
（2）①将m=−3代入二次函数的解析式即可求出n的值；
②当二次函数的y值为1时，求出x的2个值，根据m≤x≤m+1的端点可求出m的值．
【详解】（1）解：将点P−2,−2代入y=x2+ax+a−4，得4−2a+a−4=−2，解得a=2．
∴二次函数的表达式为y=x2+2x−2．
∵y=x2+2x−2=(x+1)2−3，
∴二次函数图象的顶点坐标为−1,−3．
（2）①将x=−3代入y=x2+2x−2，
得y=9−6−2=1．
∴当m=−3时，n=1．
②由（1），可知抛物线的对称轴为直线x=−1，点−3,1关于直线x=−1的对称点为1,1，如解图所示．
根据函数图象，若满足当m≤x≤m+1时，该二次函数有最小值1，则m+1=−3或m=1，
∴m=−4或m=1．
【变式7-2】（23-24九年级·湖南长沙·阶段练习）已知拋物线y=ax−ℎ2+k与x轴交于A，B两点（A在B的左边），与y轴交于点C．顶点为M．

(1)如图，若该拋物线可以由抛物线y=ax2先向右平移5个单位，在向上平移4个单位得到，点C坐标为0,−21．
（i）求A，B两点的坐标；
（ii）若线段AM的垂直平分线交x轴交于点D，交y轴交于点E，交AM交于点P，求证：四边形ADME是菱形；
(2)已知a=1，抛物线顶点M在直线y=2x−5上，若在自变量x的值满足2ℎ≤x≤2ℎ+3的情况下，对应函数值y的最小值为14，求h的值．
【答案】(1)（i）A3,0、B7,0；（ii）证明见解析；
(2)h的值为32或−152．
【分析】（1）（i）根据平移的性质和待定系数法，求出该抛物线解析式为y=−x−52+4，令y=0，求出x的值，即可得到A，B两点的坐标；
（ii）根据二次函数的性质，得到顶点M5,4，利用垂直平分线的性质，得到EA=EM，AD=DM，P4,2，再利用待定系数法和勾股定理，求出直线DE的解析式y=−12x+4，得到D8,0，进而求得AD=EM，即可证明四边形ADME是菱形；
（2）分两种情况讨论：①当ℎ≥0时；②当ℎ<0时，利用二次函数的性质，分别求出最小值方程，求解即可得到答案．
【详解】（1）（i）解：由平移性质可知，该抛物线解析式为y=ax−52+4，
∵点C0,−21在抛物线上，
∴25a+4=−21，
解得：a=−1，
∴该抛物线解析式为y=−x−52+4，
令y=0，则−x−52+4=0，
解得：x1=3，x2=7，
∵该拋物线与x轴交于A，B两点，且A在B的左边，
∴A3,0、B7,0；
（ii）证明：∵抛物线y=−x−52+4的顶点为M，
∴M5,4，
∵ED是AM的垂直平分线，
∴EA=EM，AD=DM，点P为AM的中点，
∴点P的坐标为3+52,0+42=4,2，
设直线DE的解析式为y=kx+b，
∴4k+b=2，解得：k=2−b4，
∴直线DE的解析式为y=2−b4x+b，
令x=0，则y=b，
∴E0,b，
∴EA=OE2+OA2=b2+9，EM=5−02+4−b2=b2−8b+41，
∴b2+9=b2−8b+41，
解得：b=4，
∴直线DE的解析式为y=−12x+4，E0,4，
令y=0，则−12x+4=0，
解得：x=8，
∴D8,0，
∴AD=8−3=5，
∵EM=5−02+4−42=5，
∴AD=EM，
∴EA=EM=AD=DM，
∴四边形ADME是菱形；
（2）解：∵a=1，
∴抛物线解析式y=x−ℎ2+k，
∴抛物线开口向上，对称轴为直线x=ℎ，顶点坐标Mℎ,k，
∵抛物线顶点M在直线y=2x−5上，
∴2ℎ−5=k，
①当ℎ≥0时，此时2ℎ≤x≤2ℎ+3在对称轴x=ℎ的右侧，y随x的增大而增大，
∴y的最小值为y2ℎ，
∴2ℎ−ℎ2+2ℎ−5=ℎ2+2ℎ−5=14，
解得：ℎ1=32，ℎ2=−72（舍）；
②当ℎ<0时，
若2ℎ+3<ℎ，即ℎ<−3，此时2ℎ≤x≤2ℎ+3在对称轴x=ℎ的左侧，y随x的增大而减小，
∴y的最小值为y2ℎ+3，
∴2ℎ+3−ℎ2+2ℎ−5=14，
∴ℎ2+8ℎ+4=14，
解得：ℎ1=−152，ℎ2=−12（舍）；
若2ℎ+3≥ℎ，即−3≤ℎ<0，此时对称轴x=ℎ在2ℎ≤x≤2ℎ+3的范围内，
∴y的最小值为yℎ，
∴ℎ−ℎ2+2ℎ−5=2ℎ−5=14，
解得：ℎ=218（舍），
综上可知，h的值为32或−152．
【点睛】本题是二次函数综合题，考查了二次函数的性质，待定系数法求函数解析式，垂直平分线的性质，勾股定理，菱形的判定等知识，利用分类讨论的思想，熟练掌握二次函数的性质是解题关键．
【变式7-3】（（23-24·广西贺州·二模）如图，在平面直角坐标系中，已知抛物线y=ax2+bx−3与x轴交于点A，B（点A在点B的左侧），与y轴交于点C，且OB=3OA=3．

(1)求这个二次函数的解析式；
(2)若点M是线段BC下方抛物线上的一个动点（不与点B，点C重合），过点M作直线MN⊥x轴于点D，交线段BC于点N．是否存在点M使得线段MN的长度最大，若存在，求线段MN长度的最大值，若不存在，请说明理由；
(3)当二次函数y=ax2+bx−3的自变量x满足t≤x≤t+1时，此函数的最大值与最小值的差为2，求出t的值．
【答案】(1)y=x2−2x−3
(2)存在点M使得线段MN的长度最大，最大值是94
(3)t=−12或t=32
【分析】
（1）先求出点A、B的坐标，再将点A、B的坐标代入函数表达式y=ax2+bx−3，求出a，b值，即可得答案；
（2）由题意巧设坐标，用未知数m表示出来MN的长度，根据二次函数最值问题即可解决问题；
（3）分4种情况，当t+1≤1时， t2−2t−3−t2+4=−2t+1=2，解得：t=−12；当t≥1时，t2−4−t2−2t−3=2t−1=2，解得：t=32；当t<1【详解】（1）解：∵OB=3OA=3，
∴点A、B的坐标分别为−1,0,3,0，
将点A、B的坐标代入函数表达式y=ax2+bx−3，
a−b−3=09a+3b−3=0，解得：a=1b=−2
∴抛物线的表达式为y=x2−2x−3；
（2）当x=0时，y=−3，
∴点C的坐标为0,−3，
设直线BC的关系式为y=kx+n，将B3,0,C0,−3代入y=kx+n，
3k+n=0n=−3，解得k=1n=−3
∴直线BC的关系式为y=x−3，
设Mm,m2−2m−3，则Nm,m−3，
∴MN=m−3−m2−2m−3=−m2+3m=−m−322+94
当m=32时，线段MN长度有最大值94，
∴存在点M使得线段MN的长度最大，最大值是94；
（3）
∵−b2a=−−22=1，
∴1−2−3=−4，
∴二次函数的顶点坐标是1,−4，
当x=t时，y=t2−2t−3，当x=t+1时，y=t+12−2t+1−3=t2−4，
当t+1≤1时，即t≤0，此时函数的最小值是t2−4，函数的最大值t2−2t−3，
∴t2−2t−3−t2+4=−2t+1=2，
解得：t=−12；
当t≥1时，此时函数的最小值是t2−2t−3，函数的最大值t2−4，
∴t2−4−t2−2t−3=2t−1=2，
解得：t=32；
当t<1t2−4−−4=2，
解得：t=2（舍去）或t=−2（舍去）；
当t+12<1t2−2t−3−−4=2，
解得：t=1+2（舍去）或t=1−2（舍去）；
综上所述：t=−12或t=32．
【点睛】本题考查了二次函数解析式的求法，二次函数的图像及性质，熟练掌握二次函数的图像及性质，函数图像平移的性质，数形结合，分类讨论是解题的关键．
【题型8 由二次函数的最值求字母的取值范围】
【例8】（23-24九年级·江苏南通·阶段练习）用好错题本可以有效的积累解题策略，减少再错的可能．下面是小颖同学错题本上的一道题，请仔细阅读，并完成相应任务．
任务一：请帮助小颖完成上述错题订正；
任务二：若点M2,y3也是此抛物线上的点，记抛物线在A，M之间的部分为图象G（包括M，A两点），记图形G上任意一点的纵坐标的最大值与最小值的差为t，若t≥y2−y1，直接写出m的取值范围．
【答案】任务一：①抛物线的对称轴为x=m；②a的取值范围为a=1或2【分析】本题考查二次函数的综合应用．熟练掌握二次函数的图象和性质，利用数形结合的思想进行求解是解题的关键．
任务一：①将一般式转化为顶点式即可得解；
②将Am−1,y1，Bm+2,y2代入解析式，求出y1,y2，画出函数图象，利用数形结合的方法求解即可；
任务二：分点M在点A的左侧；点A的右侧，对称轴的左侧；以及对称轴的右侧，结合图象进行分类讨论求解即可．
【详解】解：任务一：①∵ y=x2−2mx+m2+1=(x−m)2+1，
∴抛物线的对称轴为x=m；
②由y=x2−2mx+m2+1=(x−m)2+1，
得抛物线的顶点坐标为(m,1)，
当x=m−1时：y1=(m−1−m)2+1=2，
当x=m+2时：y1=(m+2−m)2+1=5，
∴ A(m−1,2)，B(m+2,5)，
∵ C(0,a)，
∴过点C垂直于y轴的直线l:y=a，如图：
由图象可知：当a=1或2∴ a的取值范围为a=1或2任务二：∵Am−1,2,Bm+2,5，
∴t≥y2−y1=5−2=3，
当x=2时，y3=m2−4m+5，
∴M2,m2−4m+5
①当M在点A的左侧，即：m−1>2，m>3时：
在对称轴的左侧，y随x的增大而减小，
∴M点的纵坐标最大，A点的纵坐标最小，
∴t=m2−4m+5−2=m2−4m+3≥3，
解得：m≥4或m≤0（舍掉）；
②当M在点A的右侧，对称轴的左侧时，此时t<2−1=1，不符合题意；
③当M对称轴的右侧，即m<2时，当y3≤2时，
此时A点的纵坐标最大，抛物线的顶点处的纵坐标最小：t=2−1=1<3不符合题意；
③当M对称轴的右侧，即m<2时，当y3>2时，
此时M点的纵坐标最大，抛物线的顶点处的纵坐标最小，
∴t=m2−4m+5−1=m2−4m+4≥3，
解得：m≥2+3（舍），或m≤2−3；
∴m≤2−3；
综上：m≤2−3或m≥4．
【变式8-1】（23-24九年级·河南郑州·阶段练习）如图，已知二次函数y=−x2+bx+c的图象经过点A4,1，点B0,5．

(1)求该二次函数的表达式，并求出对称轴和顶点坐标；
(2)点Cm,n在该二次函数图象上，当m≤x≤4时，n的最大值为294，最小值为1，请根据图象直接写出m的取值范围．
【答案】(1)表达式为y=−x2+3x+5，对称轴是：直线x=32，顶点坐标为32,294
(2)−1≤m≤32
【分析】本题主要考查了待定系数法，二次函数的图象与性质，
（1）采用待定系数法即可求解二次函数关系式，再化为顶点式即可作答；
（2）当−x2+3x+5=1，解得x=−1或x=4，可得A4,1，D−1,1，根据顶点坐标为32,294，数形结合即可作答．
【详解】（1）将点A、B的坐标分别代入二次函数，得方程组：
−16+4b+c=1c=5，
解得b=3c=5，
∴y=−x2+3x+5，
∵y=−x2+3x+5=−x−322+294，
∴对称轴是：直线x=32，顶点坐标为32,294．
答：该二次函数的表达式为y=−x2+3x+5，对称轴是：直线x=32，顶点坐标为32,294．
（2）当−x2+3x+5=1，解得x=−1或x=4，
如图，A4,1，D−1,1，顶点是E32,294，

根据题意，点C应在点E、D之间的函数图象上，可以看出，−1≤m≤32．
【变式8-2】（（23-24·浙江温州·模拟预测）已知二次函数y=ax2−2ax+3图象的一部分如图所示，它经过−1,0．
(1)求这个二次函数的表达式，并在图中补全该图象；
(2)当−2≤x≤t时，函数的最大值为m，最小值为n，若m−n=9，求t的取值范围．
【答案】(1)y=−x2+2x+3，见解析
(2)1≤t≤4
【分析】本题考查了求二次函数的解析式、二次函数的图象与性质，熟练掌握二次函数的图象与性质是解题关键．
（1）利用待定系数法可得二次函数的表达式，再利用描点法补全该图象即可得；
（2）分三种情况：−24，利用二次函数的性质求解即可得．
【详解】（1）解：将点−1,0代入y=ax2−2ax+3得：a+2a+3=0，
解得a=−1，
则这个二次函数的表达式为y=−x2+2x+3，
在图中补全该图象如下：
．
（2）解：二次函数y=−x2+2x+3=−x−12+4的顶点坐标为1,4，y的最大值为4，
当x=−2时，y=−−2−12+4=−5，
由二次函数的对称性可知，当x=2×1−−2=4时，y=−5，
①当−2则在−2≤x≤t内，y随x的增大而增大，
∴此时函数的最大值m<4，最小值n=−5，
∴m−n<9与m−n=9不符，舍去；
②当1≤t≤4时，
则在−2≤x≤t内，当−2≤x≤1时，y随x的增大而增大；当1∴此时函数的最大值m=4，最小值n=−5，
∴m−n=9，符合题意；
③当t>4时，
则在−2≤x≤t内，当−2≤x≤1时，y随x的增大而增大；当1∴此时函数的最大值m=4，最小值n<−5，
∴m−n>9与m−n=9不符，舍去，
综上，t的取值范围为1≤t≤4．
【变式8-3】（23-24九年级·湖北·周测）已知抛物线y=x2+bx+c经过点B，与y轴交于点A，顶点P在直线OB上．如图1，若点B的坐标为3,6，点P的横坐标为1．
(1)试确定抛物线的解析式；
(2)若当m≤x≤4时，y=x2+bx+c的最小值为2，最大值为11，请求出m的取值范围；
(3)已知：点M在抛物线上，点N的坐标为2,3，且∠MNA=∠BAN，请直接写出符合题意的点M的坐标．
【答案】(1)y=x2−2x+3
(2)−2≤m≤1
(3)−1,6或1,2
【分析】本题主要考查抛物线解析式的求法，抛物线顶点与对称轴的求法以及二次函数图象与性质．
（1）首先求出b的值，然后把b=−2及点B3,6的坐标代入抛物线解析式y=x2+bx+c求出c的值，抛物线的解析式即可求出；；
（2）点（4，11）关于对称轴x=1的对称点的坐标为−2,11．当m≤x≤4时，y=x2+bx+c的最小值为2，最大值为11，即可求解；
（3）当点M在直线AN上方时，由∠MNA=∠BAN，得到直线MN的表达式为：y=−x+5，进而求解；当点M在直线AN下方时，同理可解．
【详解】（1）依题意，−b2×1=1，
解得b=−2．
将b=−2及点B3,6的坐标代入抛物线解析式y=x2+bx+c得6=32−2×3+c.
解得c=3．
所以抛物线的解析式为y=x2−2x+3．
（2）由y=x2−2x+3=x−12+2知，P1,2．
∴点4,11关于对称轴x=1的对称点的坐标为−2,11．
∵当m≤x≤4时，y=x2+bx+c的最小值为2，最大值为11，
∴−2≤m≤1；
（3）由点A、N的坐标知，点A、N关于对称轴对称，则AN∥x轴，
当点M在直线AN上方时，
设直线AB的解析式为y=kx+b，
把点A0,3,B3,6的坐标代入得，
3k+b=6b=3，
解得，k=1b=3
∴AB的解析式为y=x+3，
∵∠MNA=∠BAN，
∴MN与AB的交点在对称轴上，
∴当x=1时，y=4，
∴MN与AB的交点坐标为(1,4)，
设直线MN的解析式为y=mx+n，
把2,3,1,4分别代入得2m+n=3m+n=4，
解得，m=−1n=5
则直线MN的解析式为y=−x+5，
联立y=x2−2x+3和y=−x+5并解得：
x1=−1y1=6,x2=2y2=3（不合题意，舍去），
∴M的坐标为−1,6；
当点M在直线AN下方时，
∵∠MNA=∠BAN，
∴MN∥AB,
设直线MN的表达式为：y=x+p，
当x=2时，2+p=3，解得，p=1，
∴直线MN的表达式为：y=x+1，
联立y=x2−2x+3和y=x+1并解得：
x1=1y1=2,x2=2y2=3（不合题意，舍去），
∴M的坐标为1,2；
综上，点M的坐标为：−1,6或1,2；
*年*月*日 星期天
错题***
在平面直角坐标系中，抛物线y=x2−2mx+m2+1存在两点Am−1,y1，Bm+2,y2.
①求此抛物线的对称轴；（用含m的式子表示）
②记抛物线在A，B之间的部分为图象F（包括A，B两点），y轴上一动点C(0,a)，过点C作垂直于y轴的直线l与F有且仅有一个交点，求a的取值范围；