2024-2025学年江苏省无锡市硕放中学数学九年级第一学期开学监测试题【含答案】

这是一份2024-2025学年江苏省无锡市硕放中学数学九年级第一学期开学监测试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）下列命题中，正确的是（ ）
A．平行四边形的对角线相等
B．矩形的对角线互相垂直
C．菱形的对角线互相垂直且平分
D．对角线相等的四边形是矩形
2、（4分）在下列数据6，5，7，5，8，6，6中，众数是（ ）
A．5B．6C．7D．8
3、（4分）如图，在中，，点是的中点，则下列结论不正确的是（ ）
A．B．C．D．
4、（4分）要使式子有意义，则实数的取值范围是（ ）
A．B．C．D．
5、（4分）关于▱ABCD的叙述，正确的是（ ）
A．若AB⊥BC，则▱ABCD是菱形B．若AC⊥BD，则▱ABCD是正方形
C．若AC=BD，则▱ABCD是矩形D．若AB=AD，则▱ABCD是正方形
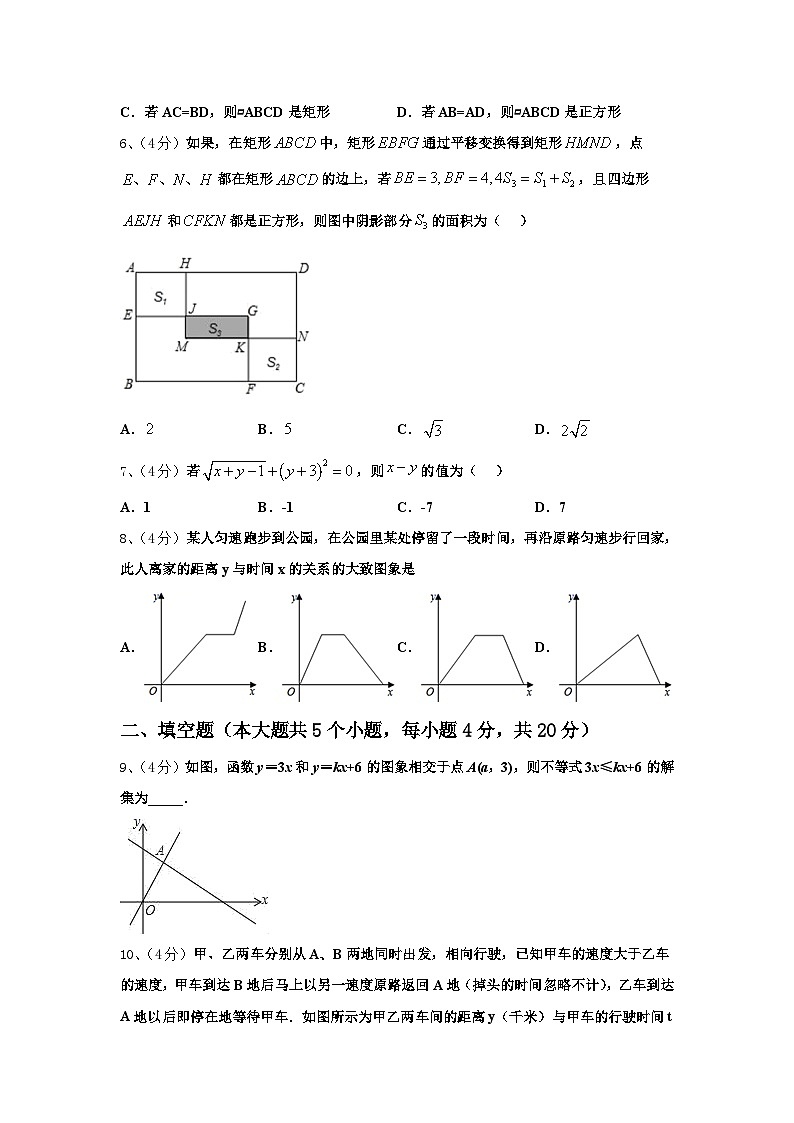
6、（4分）如果，在矩形中，矩形通过平移变换得到矩形，点都在矩形的边上，若，且四边形和都是正方形，则图中阴影部分的面积为（ ）
A．B．C．D．
7、（4分）若，则的值为（ ）
A．1B．-1C．-7D．7
8、（4分）某人匀速跑步到公园，在公园里某处停留了一段时间，再沿原路匀速步行回家，此人离家的距离y与时间x的关系的大致图象是
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，函数y＝3x和y＝kx+6的图象相交于点A(a，3)，则不等式3x≤kx+6的解集为_____．
10、（4分）甲、乙两车分别从A、B两地同时出发，相向行驶，已知甲车的速度大于乙车的速度，甲车到达B地后马上以另一速度原路返回A地（掉头的时间忽略不计），乙车到达A地以后即停在地等待甲车．如图所示为甲乙两车间的距离y（千米）与甲车的行驶时间t（小时）之间的函数图象，则当乙车到达A地的时候，甲车与A地的距离为_____千米．
11、（4分）若关于x的一元二次方程有两个不相等的实数根，则非正整数k的值是______．
12、（4分）若二次根式在实数范围内有意义，则x的取值范围是_____．
13、（4分）已知一元二次方程的两个解恰好分别是等腰的底边长和腰长，则的周长为__________．
三、解答题（本大题共5个小题，共48分）
14、（12分）某校为了了解学生的安全意识，在全校范围内随机抽取部分学生进行问卷调查．根据调查结果，把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次，并绘制成如下两幅尚不完整的统计图，如图所示：
根据以上信息，解答下列问题：
（1）这次调查一共抽取了______名学生，将条形统计图补充完整；
（2）扇形统计图中，“较强”层次所占圆心角的大小为______°；
（3）若该校有3200名学生，现要对安全意识为“淡薄”、“一般”的学生强化安全教育，根据调查结果，请你估计全校需要强化安全教育的学生人数．
15、（8分）已知与成正比例，且当时，，则当时，求的值.
16、（8分）如图，一次函数y＝kx+b（k≠0）经过点B（0，1），且与反比例函数y＝（m≠0）的图象在第一象限有公共点A（1，2）．
（1）求一次函数与反比例函数的解析式；
（2）根据图象写出当x取何值时，一次函数的值小于反比例函数的值？
17、（10分）如图，在△AOB中，∠ABO=90°，OB=1，AB=8，反比例函数y=在第一象限内的图象分别交OA，AB于点C和点D，且△BOD的面积S△BOD=1．
（1）求反比例函数解析式；
（2）求点C的坐标．
18、（10分）如图，甲、乙两船同时从A港口出发，甲船以每小时30海里的速度向西偏北32°的方向航行2小时到达C岛，乙船以每小时40海里的速度航行2小时到B岛，已知B、C两岛相距100海里，求乙船航行的方向．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）每张电影票的售价为10元，某日共售出x张票，票房收入为y元，在这一问题中，_____是常量，_____是变量．
20、（4分）学校篮球集训队11名队员进行定点投篮训练，将11名队员在1分钟内投进篮筐的球数由小到大排序后为6，7，8，9，9，9，9，10，10，10，12，这组数据的众数和中位数分别是______________.
21、（4分）如图,小明从点出发,前进5 后向右转20°,再前进5 后又向右转20°,这样一直走下去,直到他第一次回到出发点为止,他所走的路径构成了一个多边形
(1)小明一共走了________米；
(2)这个多边形的内角和是_________度.
22、（4分）在等腰△ABC中，三边分别为a、b、c，其中a=4，b、c恰好是方程的两个实数根，则△ABC的周长为__________．
23、（4分）如图，在平面直角坐标系中，O为坐标原点，矩形OABC中，A（10，0），C（0，4），D为OA的中点，P为BC边上一点．若△POD为等腰三角形，则所有满足条件的点P的坐标为 ．
二、解答题（本大题共3个小题，共30分）
24、（8分）解不等式组，并在数轴上把解集表示出来．
(1)
(2)
25、（10分）如图，在等腰梯形ABCD中，，，，.点Р从点B出发沿折线段以每秒5个单位长的速度向点C匀速运动；点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动，过点O向上作射线OKIBC，交折线段于点E．点P、O同时开始运动，为点Р与点C重合时停止运动，点Q也随之停止.设点P、Q运动的时间是t秒.
（1）点P到达终点C时，求t的值，并指出此时BQ的长；
（2）当点Р运动到AD上时，t为何值能使？
（3）t为何值时，四点P、Q、C、E成为一个平行四边形的顶点？
（4）能为直角三角形时t的取值范围________.（直接写出结果）
（注：备用图不够用可以另外画）

26、（12分）用纸复印文件，在甲复印店不管一次复印多少页，每页收费0.1元．在乙复印店复印同样的文件，一次复印页数不超过20时，每页收费0.12元；一次复印页数超过20时，超过部分每页收费0.09元．设在同一家复印店一次复印文件的页数为x（x为非负整数）
（1）根据题意，填写下表：
（2）设在甲复印店复印收费元，在乙复印店复印收费元，分别写出，关于的函数关系式；
（3）顾客如何选择复印店复印花费少？请说明理由．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据平行四边形的性质对A进行判断；根据矩形的性质对B进行判断；根据菱形的性质对C进行判断；根据矩形的判定方法对D进行判断．
【详解】
解：A、平行四边形的对角线互相平分，所以A选项错误；
B、矩形的对角线互相平分且相等，所以B选项错误；
C、菱形的对角线互相垂直且平分，所以C选项正确；
D、对角线相等的平行四边形是矩形，所以D选项错误．
故选：C．
本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部组成．熟练平行四边形和特殊平行四边形的判定与性质是解决此题的关键．
2、B
【解析】
根据众数的概念进行解答即可.
【详解】
在数据6，5，7，5，8，6，6中，数据6出现了3次，出现次数最多，
所以这组数据的众数是6，
故选B.
本题考查了众数，明确众数是指一组数据中出现次数最多的数据是解题的关键.众数一定是这组数据中的数，可以不唯一.
3、D
【解析】
首先根据三角形斜边中线定理得出AD=BD=CD,即可判定C选项正确; 又由∠A=∠ACD,∠CDB=∠A+∠ACD,即可判定A选项正确;由点是的中点，得出AD=BD,进而得出,又由,列出关系式,即可判定B选项正确;根据勾股定理,即可判定D选项错误.
【详解】
根据直角三角形斜边中线定理，得
AD=BD=CD
∴，C选项正确；
∴∠A=∠ACD
又∵∠CDB=∠A+∠ACD
∴，A选项正确；
∵点是的中点，
∴AD=BD
∴
又∵
∴
∴，B选项正确；
根据勾股定理，得
，D选项错误；
故答案为D.
此题主要考查直角三角形的性质，运用了斜边中线定理和勾股定理，熟练运用，即可解题.
4、C
【解析】
根据二次根式的性质，被开方数大于等于0，就可以求解．
【详解】
根据题意得：x−2⩾0，
解得x⩾2.
故选：C
此题考查二次根式有意义的条件，解题关键在于掌握其性质
5、C
【解析】
选项C中，满足矩形的判定定理：对角线相等的平行四边形是矩形，所以选C.
6、A
【解析】
设两个正方形的边长为x，表示出MK、JM，然后根据三个面积的关系列出方程并求出x，再求出S3.
【详解】
设两个正方形的边长为x，则MK=BF-EJ=4-x，JM=BE-KF=3-x，
∵4S3=S1+S2，
∴4（4-x）（3-x）=2x2，
整理得，x2-14x+24=0，
解得x1=2，x2=12（舍去），
∴S1=S2=22=4，
∴AB=BE+x=3+2=5，BC=BF+x=4+2=6，
∴S矩形ABCD=AB•BC=30，
∵4S3=S1+S2，
∴S3=（S1+S2）=×（4+4）=2.
故选A.
】本题考查了矩形的性质，平移的性质，平移前后的两个图形能够完全重合，关键在于表示出MK、JM并列出方程．
7、D
【解析】
首先根据非负数的性质，可列方程组求出x、y的值，进而可求出x-y的值．
【详解】
由题意，得：，
解得；
所以x-y=4-（-3）=7；
故选：D．
此题主要考查非负数的性质：非负数的和为1，则每个非负数必为1．
8、B
【解析】
图象应分三个阶段，
第一阶段：匀速跑步到公园，在这个阶段，离家的距离随时间的增大而增大；
第二阶段：在公园停留了一段时间，这一阶段离家的距离不随时间的变化而改变．故D错误；
第三阶段：沿原路匀速步行回家，这一阶段，离家的距离随时间的增大而减小，故A错误，并且这段的速度小于于第一阶段的速度，则C错误．
故选B
考点：函数的图象
本题考查了函数的图象，理解每阶段中，离家的距离与时间的关系，根据图象的斜率判断运动的速度是解决本题的关键．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、x≤1
【解析】
先利用正比例函数解析式确定点坐标，然后利用函数图象，写出直线在直线上方所对应的自变量的范围即可．
【详解】
解：把代入得，解得，则，
根据图象得，当时，．
故答案为：
本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数的值大于（或小于）0的自变量的取值范围；从函数图象的角度看，就是确定直线在轴上（或下）方部分所有的点的横坐标所构成的集合．
10、630
【解析】
分析：两车相向而行5小时共行驶了900千米可得两车的速度之和为180千米/时，当相遇后车共行驶了720千米时，甲车到达B地，由此则可求得两车的速度.再根据甲车返回到A地总用时16.5小时，求出甲车返回时的速度即可求解.
详解：设甲车，乙车的速度分别为x千米/时，y千米/时，
甲车与乙车相向而行5小时相遇，则5(x＋y)＝900，解得x＋y＝180，
相遇后当甲车到达B地时两车相距720千米，所需时间为720÷180＝4小时，
则甲车从A地到B需要9小时，故甲车的速度为900÷9＝100千米/时，乙车的速度为180－100＝80千米/时，
乙车行驶900－720＝180千米所需时间为180÷80＝2.25小时，
甲车从B地到A地的速度为900÷(16.5－5－4)＝120千米/时.
所以甲车从B地向A地行驶了120×2.25＝270千米，
当乙车到达A地时，甲车离A地的距离为900－270＝630千米.
点睛：利用函数图象解决实际问题，其关键在于正确理解函数图象横，纵坐标表示的意义，抓住交点，起点.终点等关键点，理解问题的发展过程，将实际问题抽象为数学问题，从而将这个数学问题变化为解答实际问题.
11、-1
【解析】
根据判别式的意义及一元二次方程的定义得到，且，然后解不等式即可求得k的范围，从而得出答案．
【详解】
解：根据题意知，且，
解得：且，
则非正整数k的值是，
故答案为：．
本题考查了一元二次方程的根的判别式：当，方程有两个不相等的实数根；当，方程有两个相等的实数根；当，方程没有实数根．
12、x＞2019
【解析】
根据二次根式的定义进行解答.
【详解】
在实数范围内有意义，即x-2019 0，所以x的取值范围是x 2019.
本题考查了二次根式的定义，熟练掌握二次根式的定义是本题解题关键.
13、2
【解析】
用因式分解法可以求出方程的两个根分别是3和1，根据等腰三角形的三边关系，腰应该是1，底是3，然后可以求出三角形的周长．
【详解】
x2-9x+18=0
（x-3）（x-1）=0
解得x1=3，x2=1．
由三角形的三边关系可得：腰长是1，底边是3，
所故周长是：1+1+3=2．
故答案为：2．
此题考查解一元二次方程-因式分解，解题关键在于用十字相乘法因式分解求出方程的两个根，然后根据三角形的三边关系求出三角形的周长．
三、解答题（本大题共5个小题，共48分）
14、（1）200，t图见解析；（2）108；（3）估计全校需要强化安全教育的学生人数为800人
【解析】
（1）用条形统计图中“一般”层次的人数除以扇形统计图中“一般”层次所占百分比即可求出抽取的人数，然后用总人数减去其它三个层次的人数即得“较强”层次的人数，进而可补全条形统计图；
（2）用“较强”层次的人数除以总人数再乘以360°即可求出结果；
（3）用3200乘以样本中“淡薄”和“一般”层次所占的百分比即可．
【详解】
解：（1）30÷15%=200，所以这次调查一共抽取了200名学生；
较强层次的人数为200－20－30－90=60（人），条形统计图补充为：
故答案为：200；
（2）扇形统计图中，“较强”层次所占圆心角=360°×=108°；
故答案为：108；
（3）3200×=800，所以估计全校需要强化安全教育的学生人数为800人．
本题考查了条形统计图和扇形统计图以及利用样本估计总体的思想，属于常考题型，正确理解题意、读懂统计图提供的信息、弄清二者的联系是解题的关键．
15、12.
【解析】
利用正比例函数的定义，设y=k（x-2），然后把已知的一组对应值代入求出k即可得到y与x的关系式；再将x=5代入已求解析式，从而可求出y的值.
【详解】
设，
把代入得
，
解得，
∴，
即，
当时，
.
本题考查考查了待定系数法求一次函数解析式：先设出函数的一般形式，如求一次函数的解析式时，先设y=kx+b；再将自变量x的值及与它对应的函数值y的值代入所设的解析式，得到关于待定系数的方程或方程组；然后解方程或方程组，求出待定系数的值，进而写出函数解析式．
16、（1）y＝x+1；y＝；（2）当x＜﹣2或0＜x＜1时，一次函数的值小于反比例函数的值．
【解析】
（1）把点A、B坐标代入y＝kx+b，把点A的坐标代入y＝，根据待定系数法即可求得一次函数与反比例函数的解析式；
（2）联立方程，求得得一次函数与反比例函数的图象交点坐标，然后利用函数图象的位置关系求解．
【详解】
（1）∵一次函数y＝kx+b（k≠0）经过点A（1，2），点B（0，1），
∴，解得k＝1，b＝1
∴一次函数解析式为y＝x+1；
∵点A（1，2）在反比例函数y＝的图象上，
∴m＝1×2＝2，
∴反比例函数解析式为y＝；
（2）∵方程组的解为或，
∴一次函数与反比例函数的图象交点坐标为（1，2）、（﹣2，﹣1），
∴当x＜﹣2或0＜x＜1时，一次函数的值小于反比例函数的值．
本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．也考查了待定系数法求函数解析式以及观察函数图象的能力．
17、（1）反比例函数解析式为y=；（2）C点坐标为（2，1）
【解析】
（1）由S△BOD=1可得BD的长，从而可得D的坐标，然后代入反比例函数解析式可求得k，从而得解析式为y=；
（2）由已知可确定A点坐标，再由待定系数法求出直线AB的解析式为y=2x，然后解方程组即可得到C点坐标．
【详解】
（1）∵∠ABO=90°，OB=1，S△BOD=1，
∴OB×BD=1，解得BD=2，
∴D（1，2）
将D（1，2）代入y=,
得2=,
∴k=8，
∴反比例函数解析式为y=；
（2）∵∠ABO=90°，OB=1，AB=8，
∴A点坐标为（1，8），
设直线OA的解析式为y=kx，
把A（1，8）代入得1k=8，解得k=2，
∴直线AB的解析式为y=2x，
解方程组得或，
∴C点坐标为（2，1）.
18、乙船航行的方向是东偏北58°方向．
【解析】
首先计算出甲乙两船的路程，再根据勾股定理逆定理可证明∠BAC＝90°，然后再根据C岛在A西偏北32°方向，可得B岛在A东偏北58°方向．
【详解】
解：由题意得：甲2小时的路程＝30×2＝60海里，乙2小时的路程＝40×2＝80海里，且BC＝100海里，
∵AC2+AB2＝602+802＝10000，
BC2＝1002＝10000，
∴AC2+AB2＝BC2，
∴∠BAC＝90°，
∵C岛在A西偏北32°方向，
∴B岛在A东偏北58°方向．
∴乙船航行的方向是东偏北58°方向．
此题主要考查了勾股定理逆定理，关键是掌握勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2＝c2，那么这个三角形就是直角三角形．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、电影票的售价 电影票的张数，票房收入．
【解析】
根据常量，变量的定义进行填空即可．
【详解】
解：常量是电影票的售价，变量是电影票的张数，票房收入，
故答案为：电影票的售价；电影票的张数，票房收入．
本题考查了常量和变量，掌握常量和变量的定义是解题的关键．
20、9；9
【解析】
【分析】根据中位数和众数定义可以分析出结果.
【详解】这组数据中9出现次数最多，故众数是9；按顺序最中间是9，所以中位数是9.
故答案为9；9
【点睛】本题考核知识点：众数，中位数.解题关键点：理解众数，中位数的定义.
21、90 2880
【解析】
先根据题意判断该多边形的形状，再计算该多边形的边的总长和内角和即可．
【详解】
解：由题意知，该多边形为正多边形，
∵多边形的外角和恒为360°，
360÷20=18，
∴该正多边形为正18边形．
（1）小明一共走了：5×18=90（米）；
故答案为90
（2）这个多边形的内角和为：（18-2）×180°
=2880°
故答案为2880
本题考查了正多边形的相关知识，掌握多边形的内角和定理是解决本题的关键．
22、9或10.1
【解析】
根据等腰△ABC中，当a为底，b，c为腰时，b=c，得出△=[-（2k+1）]2-4×1（k-）=4k2+4k+1-20k+11=4k2-16k+16=0，解方程求出k=2，则b+c=2k+1=1；当a为腰时，则b=4或c=4，然后把b或c的值代入计算求出k的值，再解方程进而求解即可．
【详解】
等腰△ABC中，当a为底，b，c为腰时，b=c，若b和c是关于x的方程x2-（2k+1）x+1（k-）=0的两个实数根，
则△=[-（2k+1）]2-4×1（k-）=4k2+4k+1-20k+11=4k2-16k+16=0，
解得：k=2，
则b+c=2k+1=1，
△ABC的周长为4+1=9；
当a为腰时，则b=4或c=4，
若b或c是关于x的方程x2-（2k+1）x+1（k-）=0的根，
则42-4（2k+1）+1（k-）=0，
解得：k=，
解方程x2-x+10=0，
解得x=2.1或x=4，
则△ABC的周长为：4+4+2.1=10.1．
23、（2.5，4）或（3，4）或（2，4）或（8，4）．
【解析】
试题解析：∵四边形OABC是矩形，
∴∠OCB=90°，OC=4，BC=OA=10，
∵D为OA的中点，
∴OD=AD=5，
①当PO=PD时，点P在OD得垂直平分线上，
∴点P的坐标为：（2.5，4）；
②当OP=OD时，如图1所示：
则OP=OD=5，PC==3，
∴点P的坐标为：（3，4）；
③当DP=DO时，作PE⊥OA于E，
则∠PED=90°，DE==3；
分两种情况：当E在D的左侧时，如图2所示：
OE=5-3=2，
∴点P的坐标为：（2，4）；
当E在D的右侧时，如图3所示：
OE=5+3=8，
∴点P的坐标为：（8，4）；
综上所述：点P的坐标为：（2.5，4），或（3，4），或（2，4），或（8，4）
考点：1.矩形的性质；2.坐标与图形性质；3.等腰三角形的判定；4.勾股定理．
二、解答题（本大题共3个小题，共30分）
24、（1），数轴见解析；（2），数轴见解析
【解析】
（1）分别解两个不等式，找出两个解集的公共部分，即为不等式组的解集，再将不等式组的解集在数轴上表示出来即可，
（2）分别解两个不等式，找出两个解集的公共部分，即为不等式组的解集，再将不等式组的解集在数轴上表示出来即可．
【详解】
解：（1）解不等式2x-6＜3x得：x＞-6，
解不等式得：x≤13，
∴不等式组的解集为：，
不等式组的解集在数轴上表示如下：
（2）解不等式，
解得：x，
解不等式5x-1＜3（x+1），
解得：x＜2，
即不等式组的解集为：，
不等组的解集在数轴上表示如下：
本题考查解一元一次不等式组和在数轴上表示不等式的解集，正确掌握解一元一次不等式组的方法是解题的关键．
25、 (2) 秒，；（2）详见解析；（3）；（4）或．
【解析】
（2）把BA，AD，DC它们的和求出来再除以速度每秒5个单位就可以求出t的值，然后也可以求出BQ的长；
（2）如图2，若PQ∥DC，又AD∥BC，则四边形PQCD为平行四边形，从而PD=QC，用t分别表示QC，BA，AP，然后就可以得出关于t的方程，解方程就可以求出t；
（3）分情况讨论，当P在BA上运动时，E在CD上运动．0≤t≤20，QC的长度≤30，PE的长度>AD=75，QC