2024-2025学年江苏省镇江丹徒区七校联考数学九上开学质量跟踪监视模拟试题【含答案】

这是一份2024-2025学年江苏省镇江丹徒区七校联考数学九上开学质量跟踪监视模拟试题【含答案】，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
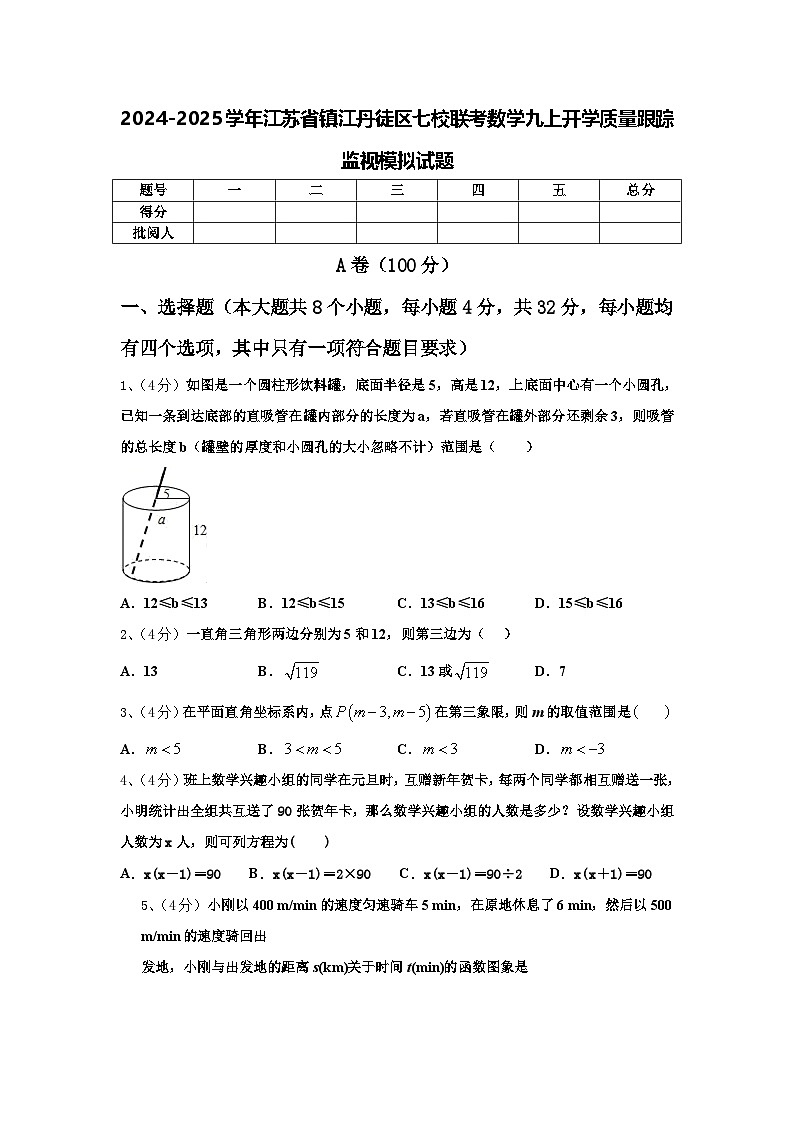
1、（4分）如图是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，已知一条到达底部的直吸管在罐内部分的长度为a，若直吸管在罐外部分还剩余3，则吸管的总长度b（罐壁的厚度和小圆孔的大小忽略不计）范围是（ ）
A．12≤b≤13B．12≤b≤15C．13≤b≤16D．15≤b≤16
2、（4分）一直角三角形两边分别为5和12，则第三边为（ ）
A．13B．C．13或D．7
3、（4分）在平面直角坐标系内，点在第三象限，则m的取值范围是
A．B．C．D．
4、（4分）班上数学兴趣小组的同学在元旦时，互赠新年贺卡，每两个同学都相互赠送一张，小明统计出全组共互送了90张贺年卡，那么数学兴趣小组的人数是多少？设数学兴趣小组人数为x人，则可列方程为( )
A．x(x－1)＝90 B．x(x－1)＝2×90 C．x(x－1)＝90÷2 D．x(x＋1)＝90
5、（4分）小刚以400 m/min的速度匀速骑车5 min，在原地休息了6 min，然后以500 m/min的速度骑回出
发地，小刚与出发地的距离s(km)关于时间t(min)的函数图象是
A．B．C．D．
6、（4分）直角三角形的边长分别为a，b，c，若a2＝9，b2＝16，那么c2的值是（ ）
A．5B．7C．25D．25或7
7、（4分）若分式有意义，则x满足的条件是（ ）
A．x≠1的实数B．x为任意实数C．x≠1且x≠﹣1的实数D．x＝﹣1
8、（4分）在平行四边形ABCD中，∠B=60°，那么下列各式中，不能成立的是（ ）
A．∠D=60°B．∠A=120°C．∠C+∠D=180°D．∠C+∠A=180°
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）在中，，则___．
10、（4分）《九章算术》是中国传统数学最重要的著作，奠定了中国传统数学的基本框架，书中的算法体系至今仍在推动着计算机的发展和应用.《九章算术》中记载：今有户不知高、广，竿不知长、短.横之不出四尺，从之不出二尺，邪之适出.问户高、广、邪各几何?译文是：今有门不知其高、宽，有竿，不知其长、短，横放，竿比门宽长出尺；竖放，竿比门高长出尺；斜放，竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为尺，则可列方程为__________．
11、（4分）若分式的值为零，则x=___________。
12、（4分）计算_________.
13、（4分）八年级（1）班安排了甲、乙、丙、丁四名同学参加4×100米接力赛，打算抽签决定四人的比赛顺序，则甲跑第一棒的概率为______．
三、解答题（本大题共5个小题，共48分）
14、（12分）若一次函数不经过第三象限，求m、n的取值范围；
15、（8分）（1）探究新知：如图1，已知与的面积相等，试判断与的位置关系，并说明理由.
（2）结论应用：
①如图2，点，在反比例函数的图像上，过点作轴，过点作轴，垂足分别为，，连接.试证明：.
②若①中的其他条件不变，只改变点，的位置如图3所示，请画出图形，判断与的位置关系并说明理由.
16、（8分）计算
（1）
（2）
17、（10分）解方程：3x-1=x2
18、（10分）计算
(1)
(2)
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）新定义：[a，b]为一次函数y＝ax+b（a≠0，a，b为实数）的“关联数”，若“关联数”[1，m﹣2]的一次函数是正比例函数，则关于x的方程x2+3x+m＝0的解为_____．
20、（4分）若方程（k为常数）有两个不相等的实数根，则k取值范围为 ．
21、（4分）如图，在平面直角坐标系xOy中，菱形AOBC的边长为8，∠AOB=60°． 点D是边OB上一动点，点E在BC上，且∠DAE=60°．
有下列结论：
①点C的坐标为（12，）；②BD=CE；
③四边形ADBE的面积为定值；
④当D为OB的中点时，△DBE的面积最小．
其中正确的有_______．（把你认为正确结论的序号都填上）
22、（4分）已知点P（3﹣m，m）在第二象限，则m的取值范围是____________________．
23、（4分）如图，在Rt△ABC中，∠ACB＝90°，点D，E分别是边AB，AC的中点，延长BC至F，使CF＝BC，若EF＝13，则线段AB的长为_____．
二、解答题（本大题共3个小题，共30分）
24、（8分）已知一次函数，.
（1）若方程的解是正数，求的取值范围；
（2）若以、为坐标的点在已知的两个一次函数图象上，求的值；
（3）若，求的值.
25、（10分）如图，在Rt△ABC中，∠C=90°，AD是∠BAC的平分线，∠CAB=60°，BD=2，求CD的长．
26、（12分）如图，在四边形ABCD中，AB∥CD，∠BCD=90°，AB=AD=10cm，BC=8cm，点P从点A出发，以每秒2cm的速度沿线段AB向点B方向运动，点Q从点D出发，以每秒3cm的速度沿线段DC向点C运动，已知动点P、Q同时出发，点P到达B点或点Q到达C点时，P、Q运动停止，设运动时间为t (秒)．
（1）求CD的长；
（2）当四边形PBQD为平行四边形时，求t的值；
（3）在点P、点Q的运动过程中，是否存在某一时刻，使得PQ⊥AB？若存在，请求出t的值并说明理由；若不存在，请说明理

参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
此题涉及的知识点是解直角三角形，根据题目中底面半径是5，高是12，可以算出另一边，吸管在罐外部分剩余3，不同放置就可以算出总长
【详解】
底面半径是5，高是12，则吸管最长放在罐里的长度为13，加上罐外的3，总长为16；如果吸管竖直放置，则罐里最短长为12，加上罐外3总长为15，所以吸管总长范围为：
故选D
此题重点考察学生对直角三角形的解的应用，勾股定理是解题的关键
2、C
【解析】
此题要考虑两种情况：当所求的边是斜边时；当所求的边是直角边时．
【详解】
由题意得：当所求的边是斜边时，则有=1；
当所求的边是直角边时，则有=．
故选：C．
本题考查了勾股定理的运用，难度不大，但要注意此类题的两种情况，很多学生只选1．
3、C
【解析】
由于在平面直角坐标系内,点在第三象限,根据点在平面直角坐标系内符号特征可得:,解不等式组可得:不等式组的解集是.
【详解】
因为点在第三象限,
所以,
解得不等式组的解集是,
故选C.
本题主要考查点在平面直角坐标系内符号特征,解决本题的关键是要熟练掌握点在平面直角坐标系内点的符号特征.
4、A
【解析】
如果设数学兴趣小组人数为x人，每名学生送了（x﹣1）张，共有x人，则一共送了x（x﹣1）张，再根据“共互送了1张贺年卡”，可得出方程为x（x﹣1）＝1．
【详解】
设数学兴趣小组人数为x人，每名学生送了（x﹣1）张，共有x人，根据“共互送了1张贺年卡”，可得出方程为x（x﹣1）＝1．
故选A．
本题考查了一元二次方程的应用．解题的关键是读清题意，找准数量关系，列出方程．
5、C
【解析】
【分析】根据题意分析在各个时间段小刚离出发点的距离，结合图象可得出结论.
【详解】由已知可得，前5min小刚与出发地相距2千米，后6min距离不变，之后距离逐渐减少.故选项C符合实际情况.
故选：C
【点睛】本题考核知识点：函数的图形. 解题关键点：结合实际分析函数图像.
6、D
【解析】
此题有两种情况：①当a，b为直角边，c为斜边，由勾股定理求出c2即可；②当a，c为直角边，b为斜边，利用勾股定理即可求解；即可得出结论．
【详解】
解：当b为直角边时，c2＝a2+b2＝25，
当b为斜边时，c2＝b2﹣a2＝7，
故选：D．
此题主要考查学生对勾股定理的理解和掌握；解答此题要用分类讨论的思想，学生容易忽略a，c为直角边，b为斜边时这种情况，很容易选A，因此此题是一道易错题．
7、A
【解析】
直接利用分式有意义的条件得出：x﹣1≠0，解出答案．
【详解】
解：∵分式有意义，
∴x﹣1≠0，
解得：x≠1．
∴x满足的条件是：x≠1的实数．
故选A．
此题主要考查了分式有意义的条件，正确把握分式的定义是解题关键．
8、D
【解析】
解：∵四边形ABCD是平行四边形，∴∠D＝∠B＝60°．故A正确；
∵AD∥BC，∴∠A＋∠B＝180°，∴∠A＝180°－∠B＝120°，故B正确；
∵AD∥BC，∴∠C＋∠D＝180°，故C正确；
∵四边形ABCD是平行四边形，∴∠C＝∠A＝120°，故D不正确，
故选D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、．
【解析】
根据平行四边形的性质可得：∠A=∠C，∠A+∠B=180°；再根据∠A+∠C=120°计算出∠A的度数，进而可算出∠B的度数.
【详解】
四边形是平行四边形，
，，
，
，
．
故答案为：．
本题是一道有关平行四边形的题目，掌握平行四边形的性质是解题关键.
10、．
【解析】
根据题中所给的条件可知，竿斜放就恰好等于门的对角线长，可与门的宽和高构成直角三角形，运用勾股定理可求出门高、宽、对角线长．
【详解】
解：根据勾股定理可得：
，即x2-8x+16+x2-4x+4= x2，
解得：x1=2（不合题意舍去），x2=10，
10-2=8（尺），
10-4=6（尺）．
答：门高8尺，门宽6尺，对角线长10尺．
故答案为： ．
本题考查勾股定理的运用，正确运用勾股定理，将数学思想运用到实际问题中是解题的关键．
11、1
【解析】
根据分式的值为零的条件可以求出x的值.
【详解】
解: ∵分式的值为零
∴
∴且
∴ 且
∴x=1
故答案为：x=1
若分式的值为零，需同时具备两个条件：（1）分子为1；（2）分母不为1．这两个条件缺一不可．
12、19+6
【解析】
根据完全平方公式展开计算即可。
【详解】
解：18+6+1=19+6
本题考查了用完全平方公式进行实数的计算，理解和掌握乘法公式是关键。
13、
【解析】
【分析】抽签有4种可能的结果，其中抽到甲的只有一种结果，根据概率公式进行计算即可得.
【详解】甲、乙、丙、丁四人都有机会跑第一棒，而且机会是均等的，
抽签抽到甲跑第一棒有一种可能，
所以甲跑第一棒的概率为，
故答案为：.
【点睛】本题考查了简单的概率计算，用到的知识点为：概率=所求情况数与总情况数之比．
三、解答题（本大题共5个小题，共48分）
14、
【解析】
根据一次函数的图像不经过第三象限得到k＜0，b≥0，故可求解.
【详解】
题意有：
解得
此题主要考查一次函数的图像，解题的关键是熟知一次函数的图像与性质.
15、（1），理由见解析；（2）①见解析；②，理由见解析.
【解析】
（1）分别过点C，D，作CG⊥AB，DH⊥AB，垂足为G，H，则∠CGA=∠DHB=90°，根据△ABC与△ABD的面积相等，证明AB与CD的位置关系；
（2）连结MF，NE，设点M的坐标为（x1，y1），点N的坐标为（x2，y2），进一步证明S△EFM=S△EFN，结合（1）的结论即可得到MN∥EF；
（3）连接FM、EN、MN，结合（2）的结论证明出MN∥EF，GH∥MN，于是证明出EF∥GH．
【详解】
（1）如图1，分别过点、作、，垂足分别为、，
则，
∴，
∵且，
，
∴，
∴四边形为平行四边形，
∴；
（2）①如图2，连接，，
设点的坐标为，点的坐标为，
∵点，在反比例函数的图像上，
∴，.
∵轴，轴，且点，在第一象限，
∴，，，.
∴，，
∴，
从而，由（1）中的结论可知：；
②如图
，
理由：连接，，
设点的坐标为，点的坐标为，
由（2）①同理可得：
，，
∴，
从而，由（1）中的结论可知：.
本题主要考查反比例函数的综合题，解答本题的关键是根据同底等高的两个三角形面积相等进行解答问题，此题难度不是很大，但是三问之间都有一定的联系．
16、（1）（2）
【解析】
（1）先化成最简二次根式，再合并同类二次根式即可；
（2）根据多项式除以单项式法则展开，再进行计算即可．
【详解】
解：（1）原式=
=
（2）原式=
=
本题考查了二次根式的加减混合运算的应用，主要考查学生的计算能力．
17、x1=，x2=．
【解析】
方程整理后，利用公式法求出解即可．
【详解】
解：方程整理得：x2-3x+1=0，
这里a=1，b=-3，c=1，
∵△=9-4=5，
∴x=，
解得：x1=，x2=．
此题考查了解一元二次方程-公式法，以及配方法，熟练掌握各种解法是解本题的关键．
18、.(1) ； (2)
【解析】
（1）首先将二次根式化为最简二次根式，然后根据二次根式的乘除运算法则计算即可；
（2）首先将二次根式化为最简二次根式，然后根据二次根式的乘除运算法则计算即可．
【详解】
解：（1）原式＝；
（2）原式＝.．
本题考查二次根式的乘除运算，解题的关键是熟练运用二次根式的性质和运算法则．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、x1＝﹣1，x1＝﹣1．
【解析】
利用题中的新定义求出m的值，代入一元二次方程，运用因式分解法解方程，即可求出解．
【详解】
解：由“关联数”定义得一次函数为y＝x+m﹣1，
又∵此一次函数为正比例函数，∴m﹣1＝0，
解得：m＝1，
∴关于x的方程为x1+3x+1＝0，
因式分解得：（x+1）（x+1）＝0，
∴x+1＝0或x+1＝0，
∴x1＝﹣1，x1＝﹣1；
故答案为x1＝﹣1，x1＝﹣1．
本题考查新定义“关联数”、一元二次方程的解法以及一次函数的定义，弄清题中的新定义是解本题的关键．
20、
【解析】
根据方程的系数结合根的判别式即可得出关于k的一元一次不等式，解不等式即可得出结论，
【详解】
解：∵方程（k为常数）的两个不相等的实数根，
∴>0，且，
解得：k3.
【解析】
试题分析：因为点P在第二象限，所以，，解得：
考点：（1）平面直角坐标；（2）解不等式组
23、1
【解析】
根据三角形中位线定理得到，，根据平行四边形的性质求出，根据直角三角形的性质计算即可．
【详解】
解：点，分别是边，的中点，
，，
，
，又，
四边形为平行四边形，
，
，点是边的中点，
，
故答案为：1．
本题考查的是直角三角形的性质、三角形中位线定理，掌握在直角三角形中，斜边上的中线等于斜边的一半是解题的关键．
二、解答题（本大题共3个小题，共30分）
24、（1）；（2）；（3）－2
【解析】
（1）根据代入求出x的解，得到a的不等式即可求解；
（2）联立两函数求出交点坐标，代入即可求解；
（3）根据分式的运算法则得到
得到A，B的方程，即可求解.
【详解】
（1）∵
∴
由题意可知，即，解得.
（2）由题意可知为方程组的解，解方程组得.
所以，，
将代入上式得：.
（3）∵
∴，解得.所以的值为.
此题主要考查一次函数的应用，解题的关键是熟知一次函数的性质、二元一次方程组的解法.
25、1
【解析】
根据角平分线的定义得到∠CAD=∠CAB=30°，根据三角形的内角和得到∠B=30°，根据直角三角形的性质即可得到结论．
【详解】
∵AD是∠BAC的平分线，∠CAB=60°，
∴∠CAD=∠CAB=30°，
∵∠C=90°，∠CAB=60°，
∴∠B=30°，
∴AD=BD=2，
∵∠CAD=30°，
∴CD=AD=1．
本题考查了解直角三角形，锐角三角函数，角平分线的定义等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
26、（1）1；（2）2；（3）不存在．理由见解析
【解析】
【分析】（1）作AM⊥CD于M，由勾股定理求AM，再得CD=DM+CM=DM+AB；
（2）由题意：BP=AB﹣AP=10﹣2t．DQ=3t，根据：当BP=DQ时，四边形PBQD是平行四边形，可得10﹣2t=3t,可求t；
（3）作AM⊥CD于M，连接PQ．假设存在，则AP=MQ=3t﹣6，即2t=3t﹣6，求出的t不符合题意，故不存在.
【详解】解（1）如图1，作AM⊥CD于M，
则由题意四边形ABCM是矩形，
在Rt△ADM中，
∵DM2=AD2﹣AM2，AD=10，AM=BC=8，
∴AM=
=6，
∴CD=DM+CM=DM+AB=6+10=1．
（2）当四边形PBQD是平行四边形时，点P在AB上，点Q在DC上，
如图2中，由题意：BP=AB﹣AP=10﹣2t．DQ=3t，
当BP=DQ时，四边形PBQD是平行四边形，
∴10﹣2t=3t，
∴t=2，
（3）不存在．理由如下：
如图3，作AM⊥CD于M，连接PQ．
由题意AP=2t．DQ=3t，
由（1）可知DM=6，∴MQ=3t﹣6，
若2t=3t﹣6， 解得t=6，
∵AB=10，
∴t≤=5，
而t=6＞5，故t=6不符合题意，t不存在．
【点睛】本题考核知识点：动点，平行四边形，矩形. 解题关键点：此题是综合题，熟记性质和判定是关键.
题号
一
二
三
四
五
总分
得分
批阅人