2024-2025学年上海市静安区名校数学九年级第一学期开学学业水平测试模拟试题【含答案】

这是一份2024-2025学年上海市静安区名校数学九年级第一学期开学学业水平测试模拟试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为（）
A．（，1）B．（2，1）
C．（2，）D．（1，）
2、（4分）已知一次函数不过第二象限，则b试问取值范围是（ ）
A．b0C．b≤0D．b≥0
3、（4分）以下命题，正确的是（ ）.
A．对角线相等的菱形是正方形
B．对角线相等的平行四边形是正方形
C．对角线互相垂直的平行四边形是正方形
D．对角线互相垂直平分的四边形是正方形
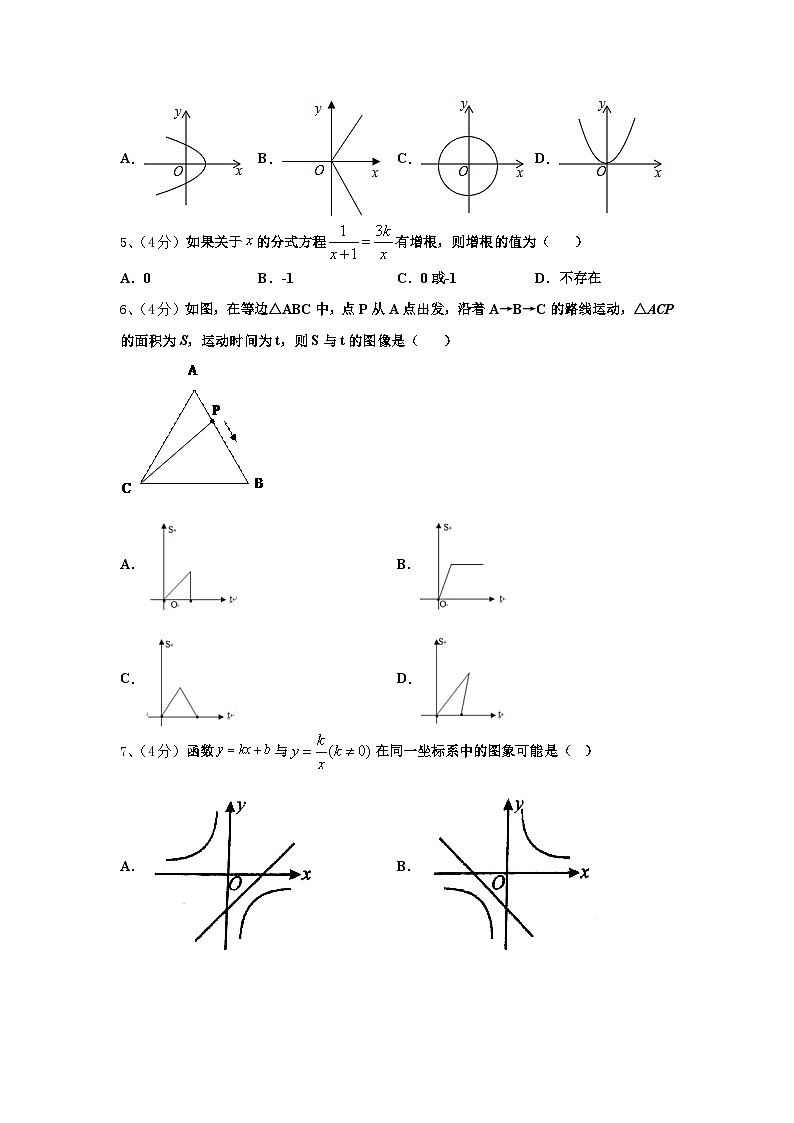
4、（4分）下列曲线中能表示y是x的函数的为（ ）
A．B．C．D．
5、（4分）如果关于的分式方程有增根，则增根的值为（ ）
A．0B．-1C．0或-1D．不存在
6、（4分）如图，在等边△ABC中，点P从A点出发，沿着A→B→C的路线运动，△ACP的面积为S，运动时间为t，则S与t的图像是（ ）
A．B．
C．D．
7、（4分）函数与在同一坐标系中的图象可能是（ ）
A．B．
C．D．
8、（4分）下列关于一元二次方程x2+bx+c＝0的四个命题
①当c＝0，b≠0时，这个方程一定有两个不相等的实数根；
②当c≠0时，若p是方程x2+bx+c＝0的一个根，则是方程cx2+bx+1＝0的一个根；
③若c＜0，则一定存在两个实数m＜n，使得m2+mb+c＜0＜n2+nb+c；
④若p，q是方程的两个实数根，则p﹣q＝，
其中是假命题的序号是（ ）
A．①B．②C．③D．④
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，在中，，D是AB的中点，若，则的度数为________。
10、（4分）小明用100元钱去购买笔记本和钢笔共30件，已知每本笔记本2元，每枝钢笔5元，那么小明最多能买________枝钢笔．
11、（4分）如图，边长为2的正方形ABCD中，AE平分∠DAC，AE交CD于点F，CE⊥AE，垂足为点E，EG⊥CD，垂足为点G，点H在边BC上，BH＝DF，连接AH、FH，FH与AC交于点M，以下结论：①FH＝2BH；②AC⊥FH；③S△ACF＝1；④CE＝AF；⑤EG2＝FG•DG，其中正确结论的有_____（只填序号）．
12、（4分）如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是__________．
13、（4分）已知一次函数y=kx+b的图象交y轴于正半轴，且y随x的增大而减小，请写出符合上述条件的一个解析式：_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，已知直线 :与x轴，y轴的交点分别为A，B，直线 : 与y轴交于点C，直线与直线的交点为E，且点E的横坐标为2.
（1）求实数b的值；
（2）设点D（a，0）为x轴上的动点，过点D作x轴的垂线，分别交直线与直线于点M、N，若以点B、O、M、N为顶点的四边形是平行四边形，求a的值.
15、（8分）阅读材料，回答问题：
材料：将一个多项式分组后，可提公因式或运用公式继续分解的方法是因式分解中的分组分解法，一般的分组分解法有四种形式，即“”分法、“”分法、“”分法及“”分法等．
如“”分法：
请你仿照以上方法，探索并解决下列问题：
分解因式：（1）；
（2）．
16、（8分）如图，直线l1：y1=−x+m与y轴交于点A（0，6），直线l2：y2=kx+1分别与x轴交于点B（-2，0），与y轴交于点C．两条直线相交于点D，连接AB．
（1）求两直线交点D的坐标；
（2）求△ABD的面积；
（3）根据图象直接写出y1＞y2时自变量x的取值范围．
17、（10分）如图，矩形ABCD中，AB=2，BC=5，E、P分别在AD、BC上，且DE=BP=1．
（1）断⊿BEC的形状，并说明理由；
（2）判断四边形EFPH是什么特殊四边形？并证明你的判断．
18、（10分）如图1，为美化校园环境，某校计划在一块长为20m，宽为15m的长方形空地上修建一条宽为a（m）的甬道，余下的部分铺设草坪建成绿地．
（1）甬道的面积为 m2，绿地的面积为 m2（用含a的代数式表示）；
（2）已知某公园公司修建甬道，绿地的造价W1（元），W2（元）与修建面积S之间的函数关系如图2所示．①园林公司修建一平方米的甬道，绿地的造价分别为 元， 元．②直接写出修建甬道的造价W1（元），修建绿地的造价W2（元）与a（m）的关系式；③如果学校决定由该公司承建此项目，并要求修建的甬道宽度不少于2m且不超过5m，那么甬道宽为多少时，修建的甬道和绿地的总造价最低，最低总造价为多少元？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，反比例函数 y＝的图象经过矩形 OABC 的一个顶点 B，则矩形 OABC 的面积等于___．
20、（4分）若，则= ．
21、（4分）如图中的螺旋由一系列直角三角形组成，则第2019个三角形的面积为_______.
22、（4分）如图，在▱ABCD中（AD＞AB），用尺规作图作射线BP交AD于点E，若∠D＝50°，则∠AEB＝___度．
23、（4分）反比例函数y=的图像在其每一象限内，y随x的增大而减小，则k的值可以是______.(写出一个数值即可）
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在平面直角坐标系中，直线y=x+2与x轴、y轴分别交于A、B两点，以A B为边在第二象限内作正方形ABCD．
（1）求点A、B的坐标，并求边AB的长；
（2）求点D的坐标；
（3）在x轴上找一点M，使△MDB的周长最小，请求出M点的坐标．
25、（10分）已知：如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．
(1)求证：△ADE≌△CBF；
(2)若四边形BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论．
26、（12分）先化简，再求的值，其中x=2
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
由已知条件得到AD′=AD=2，AO=AB=1，根据勾股定理得到OD′=，于是得到结论．
【详解】
解：∵AD′=AD=2，
AO=AB=1，
OD′=，
∵C′D′=2，C′D′∥AB，
∴C′（2，），
故选D．
本题考查了正方形的性质，坐标与图形的性质，勾股定理，正确的识别图形是解题的关键．
2、C
【解析】
根据题意可知：图象经过一三象限或一三四象限，可得b=1或b＜1，再解不等式可得答案．
【详解】
解：一次函数的图象不经过第二象限，
则可能是经过一三象限或一三四象限，
若经过一三象限时，b=1；
若经过一三四象限时，b＜1．
故b≤1，
故选C．
此题主要考查了一次函数图象在坐标平面内的位置与k、b的关系．解答本题注意理解：直线y=kx+b所在的位置与k、b的符号有直接的关系．k＞1时，直线必经过一、三象限；k＜1时，直线必经过二、四象限；b＞1时，直线与y轴正半轴相交；b=1时，直线过原点；b＜1时，直线与y轴负半轴相交．
3、A
【解析】
利用正方形的判定方法分别判断后即可确定正确的选项．
【详解】
A、对角线相等的菱形是正方形，正确，是真命题；
B、对角线相等的平行四边形是矩形，故错误，是假命题；
C、对角线互相垂直的平行四边形是菱形，故错误，是假命题；
D、对角线互相垂直平分的四边形是菱形，故错误，是假命题，
故选：A．
考查了命题与定理的知识，解题的关键是了解正方形的判定方法．
4、D
【解析】
根据函数的定义可知，满足对于x的每一个取值，y都有唯一确定的值与之对应关系，据此即可判断．
【详解】
A、B、C选项，一个x的值对应有两个y值，故不能表示y是x的函数，错误，
D选项，x的每一个值，y都有唯一确定的值与它对应，正确，
故选D．
本题考查了函数的定义．函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．
5、A
【解析】
先把分式方程化成整式方程，再解整式方程求出x的值，根据方程有增根得出或，解出k的值即可得出答案.
【详解】
又方程有增根
∴或
无解或k=0
∴k=0
∴增根的值为0
故答案选择A.
本题考查的是分式方程的增根问题，属于基础题型，解题关键是根据增根得出整式方程有解，而分式方程无解，即整式方程求出的解使得分式方程的分母等于0.
6、C
【解析】
当点A开始沿AB边运动到点B时，△ACP的面积为S逐渐变大；当点A沿BC边运动到点C时，△ACP的面积为S逐渐变小. , ∴由 到 与由 到 用的时间一样.故选C.
7、D
【解析】
根据k值的正负，判断一次函数和反比例函数必过的象限，二者一致的即为正确答案．
【详解】
在函数与中，
当k>0时，图象都应过一、三象限；
当k