2022-2023学年河南省郑州市新郑市龙湖四中七（上）第一次月考数学试卷及答案

这是一份2022-2023学年河南省郑州市新郑市龙湖四中七（上）第一次月考数学试卷及答案，共17页。试卷主要包含了解答题等内容，欢迎下载使用。
1．（3分）﹣8的相反数是（ ）
A．8B．C．D．﹣8
2．（3分）生活中的实物可以抽象出各种各样的几何图形，如图所示的不锈钢漏斗的形状类似于（ ）
A．圆B．球C．圆柱D．圆锥
3．（3分）手机移动支付给生活带来便捷．如图是张老师某日微信账单的收支明细（正数表示收入，负数表示支出，单位：元），张老师当天微信收支的最终结果是（ ）
A．收入15元B．支出2元C．支出17元D．支出9元
4．（3分）下列说法中正确的是（ ）
A．数轴上距离原点2个单位长度的点表示的数是2
B．﹣1是最大的负整数
C．任何有理数的绝对值都大于0
D．0是最小的有理数
5．（3分）如图，点A，B，C表示的数分别记为a，b，c，数轴的单位长度为1，如果点B，C表示的数的绝对值相等，那么a的值为（ ）
A．﹣2B．﹣4C．﹣6D．6
6．（3分）若将一根底面半径是5厘米的圆柱体木料锯成三段（每段都是圆柱体），则其表面积增加了（ ）
A．25π平方厘米B．50π平方厘米
C．75π平方厘米D．100π平方厘米
7．（3分）若规定[x）表示大于x的最小整数，[5）＝6，[﹣1.8）＝﹣1，则下列结论错误的是（ ）
A．[﹣3.1）＝﹣4B．[2.2）＝3C．[0）＝1D．
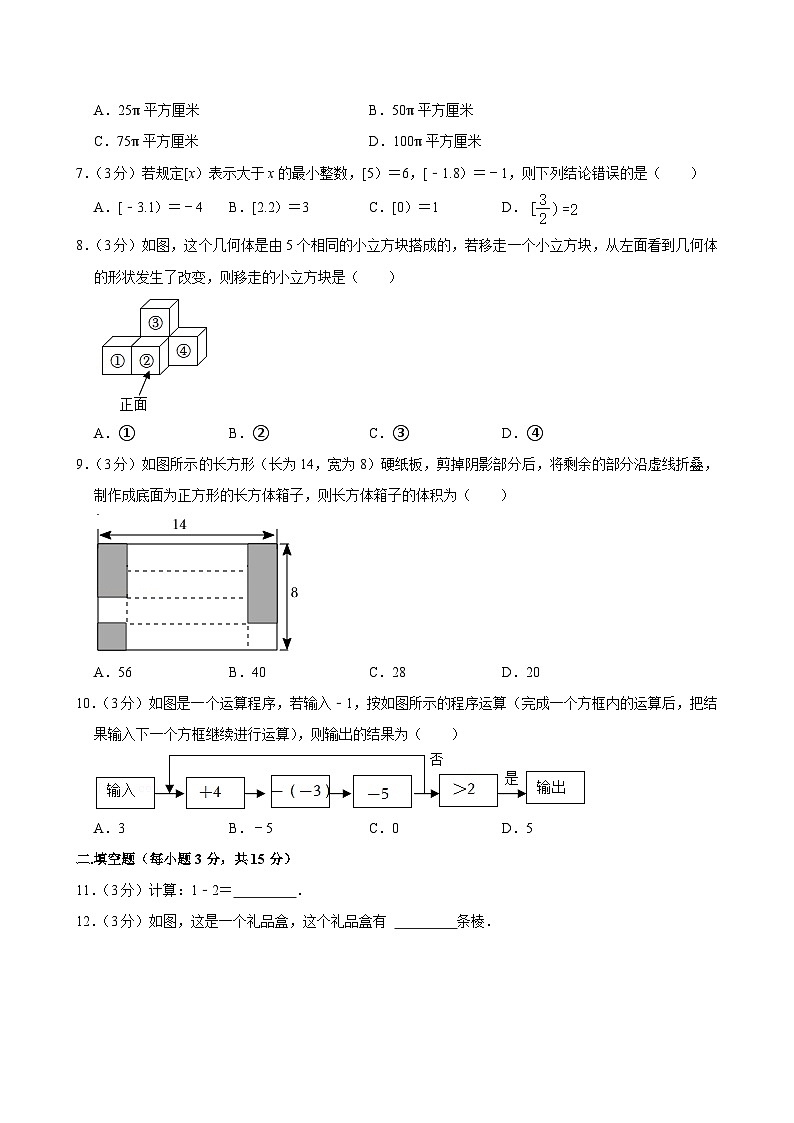
8．（3分）如图，这个几何体是由5个相同的小立方块搭成的，若移走一个小立方块，从左面看到几何体的形状发生了改变，则移走的小立方块是（ ）
A．①B．②C．③D．④
9．（3分）如图所示的长方形（长为14，宽为8）硬纸板，剪掉阴影部分后，将剩余的部分沿虚线折叠，制作成底面为正方形的长方体箱子，则长方体箱子的体积为（ ）
A．56B．40C．28D．20
10．（3分）如图是一个运算程序，若输入﹣1，按如图所示的程序运算（完成一个方框内的运算后，把结果输入下一个方框继续进行运算），则输出的结果为（ ）
A．3B．﹣5C．0D．5
二.填空题（每小题3分，共15分）
11．（3分）计算：1﹣2＝ ．
12．（3分）如图，这是一个礼品盒，这个礼品盒有 条棱．
13．（3分）某天最高气温为6℃，最低气温为﹣3℃．这天的温差是 ℃．
14．（3分）用一个平面去截一个三棱柱，截面图形的边数最多的为 边形．
15．（3分）已知|a|＝1，|b|＝2，|c|＝3，且b＞a＞c，则a+b+c的值为 ．
三、解答题（本题共8个小题，共75分）
16．（10分）（1）计算：20+（﹣14）﹣（﹣18）﹣|﹣13|．
（2）在计算“”时．甲同学的做法如下：
在甲同学的计算过程中，开始出错的步骤是 （写出错误所在行的序号），请你写出正确的计算过程．
17．（9分）在数轴上表示下列各数：，﹣3.5，﹣1.6，﹣，﹣4，2.5．并用“＜”把这些数连接起来．
18．（9分）如图，这是由8个大小相同的小立方块搭建的几何体，请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图．
19．（9分）（1）如图，下面两个图分别表示负数集合和分数集合，请你把下列各数填入它所在数集的圈里．
3.5，﹣25%，0，，﹣5，3，﹣2，．
（2）在（1）图中两个圈的重叠部分表示 数的集合．
（3）列式并计算：在（1）的数据中，求最大的数与最小的数的和．
20．（9分）请根据图示的对话解答下列问题．
（1）分别求出a和b的值．
（2）已知|m﹣a|+|b+n|＝0，求m﹣n的值．
21．（9分）郑州到南阳有一列高铁从起点郑州东站经过新郑机场，郑州航空港，郑县，方城站到达终点南阳东站，一路上下乘客人数如表所示．（用正数表示上车的人数，负数表示下车的人数）
（1）问到南阳东站下车的有多少人？
（2）问高铁行驶在哪两站之间车上的乘客最多？
22．（10分）【问题情境】
小圣所在的综合实践小组准备制作一些无盖纸盒收纳班级讲台上的粉笔．
【操作探究】
（1）图1中的哪些图形经过折叠能围成无盖正方体纸盒？ （填序号）．
（2）小圣所在的综合实践小组把折叠成6个棱长都为2dm的无盖正方体纸盒摆成如图2所示的几何体．
①请计算出这个几何体的体积；
②如果在这个几何体上再添加一些相同的正方体纸盒，并保持从上面看到的形状和从左面看到的形状不变，最多可以再添加 个正方体纸盒．
23．（10分）如图，甲、乙两人（看成点）分别在数轴﹣6和9的位置上，沿数轴做移动游戏．移动游戏规则；两人先进行“石头，剪刀、布”，而后根据输赢结果进行移动．
①若平局，则甲向东移动1个单位长度，同时乙向西移动1个单位长度；
②若甲赢，则甲向东移动5个单位长度，同时乙向东移动3个单位长度；
③若乙赢，则甲向西移动3个单位长度，同时乙向西移动5个单位长度．
前三局如表：（提示：剪刀胜布，布胜石头，石头胜剪刀）
（1）从如图所示的位置开始，求第一局后甲、乙两人分别在数轴上的位置．
（2）从如图所示的位置开始，从前三局看，第几局后甲离原点最近，离原点距离多少？
（3）从如图所示的位置开始，若进行了k局后，甲与乙的位置相距3个单位长度，请直接写出k的值．
2022-2023学年河南省郑州市新郑市龙湖四中七年级（上）第一次月考数学试卷
参考答案与试题解析
一、选择题(每小题3分,共30分)下列各小题均有四个选项,其中只有一个是正确的,请把正确答案的代号填在表中。
1．（3分）﹣8的相反数是（ ）
A．8B．C．D．﹣8
【分析】根据相反数的定义进行解答即可．
【解答】解：﹣8的相反数是8，
故选：A．
【点评】本题考查相反数，理解相反数的定义是正确解答的前提．
2．（3分）生活中的实物可以抽象出各种各样的几何图形，如图所示的不锈钢漏斗的形状类似于（ ）
A．圆B．球C．圆柱D．圆锥
【分析】根据图形直接得到答案．
【解答】解：不锈钢漏斗的形状类似于圆锥，
故选：D．
【点评】此题主要考查了认识立体图形，关键是结合实物，认识常见的立体图形，如：长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等．能区分立体图形与平面图形，立体图形占有一定空间，各部分不都在同一平面内．
3．（3分）手机移动支付给生活带来便捷．如图是张老师某日微信账单的收支明细（正数表示收入，负数表示支出，单位：元），张老师当天微信收支的最终结果是（ ）
A．收入15元B．支出2元C．支出17元D．支出9元
【分析】根据正负数的意义以及有理数的加法法则求和即可．
【解答】解：15+（﹣8）+（﹣9）＝﹣2（元），
即张老师当天微信收支的最终结果是支出2元．
故选：B．
【点评】本题考查了正数和负数，掌握正数和负数表示相反意义的量是解题的关键．
4．（3分）下列说法中正确的是（ ）
A．数轴上距离原点2个单位长度的点表示的数是2
B．﹣1是最大的负整数
C．任何有理数的绝对值都大于0
D．0是最小的有理数
【分析】根据数轴上到一点距离相等的点有两个，可判断A；根据整数，可判断B；根据绝对值的意义，可判断C；根据有理数，可判断D．
【解答】解：A、数轴上距离原点2个单位长度的点表示的数是2或﹣2，故A错误；
B、﹣1是最大的负整数，故B正确；
C、0的绝对值等于零，故C错误；
D、没有最小的有理数，故D错误；
故选：B．
【点评】本题考查了有理数，没有最大的有理数，也没有最小的有理数．
5．（3分）如图，点A，B，C表示的数分别记为a，b，c，数轴的单位长度为1，如果点B，C表示的数的绝对值相等，那么a的值为（ ）
A．﹣2B．﹣4C．﹣6D．6
【分析】根据B、C表示的数的绝对值相等，可得原点的位置，根据原点的位置，可得A点表示的数．
【解答】解：如图：
由点B，C表示的数的绝对值相等，得原点O的位置，
∴A点表示的数是﹣4，
故选：B．
【点评】本题考查了数轴，利用绝对值相等的点关原点对称得出原点的位置是解题关键．
6．（3分）若将一根底面半径是5厘米的圆柱体木料锯成三段（每段都是圆柱体），则其表面积增加了（ ）
A．25π平方厘米B．50π平方厘米
C．75π平方厘米D．100π平方厘米
【分析】把圆柱锯成3段后，表面积比原来增加了2×2＝4个圆柱的底面积，由此根据圆柱的底面半径求出圆柱的底面积，再乘以4，即可解决问题．
【解答】解：把圆柱锯成3段后，表面积比原来增加了2×2＝4个圆柱的底面积，
∴表面积增加了：π×52×4＝100π平方厘米，
故选：D．
【点评】本题考查了圆柱底面积计算，明确将圆柱锯成3段后，表面积比原来增加了4个圆柱的底面积是解题的关键．
7．（3分）若规定[x）表示大于x的最小整数，[5）＝6，[﹣1.8）＝﹣1，则下列结论错误的是（ ）
A．[﹣3.1）＝﹣4B．[2.2）＝3C．[0）＝1D．
【分析】根据题意，逐一进行判断即可．
【解答】解：A、[﹣3.1）＝﹣3，选项错误，符合题意；
B、[2.2）＝3，选项正确，不符合题意；
C、[0）＝1，选项正确，不符合题意；
D、，选项正确，不符合题意；
故选：A．
【点评】本题考查有理数比较大小．理解并掌握题干中的规定，是解题的关键．
8．（3分）如图，这个几何体是由5个相同的小立方块搭成的，若移走一个小立方块，从左面看到几何体的形状发生了改变，则移走的小立方块是（ ）
A．①B．②C．③D．④
【分析】根据从左面看到的图形是左视图解答即可．
【解答】解：这个几何体是由5个相同的小立方块搭成的，若移走一个小立方块，从左面看到几何体的形状发生了改变，则移走的小立方块是③．
故选：C．
【点评】此题考查的是简单组合体的三视图，掌握其相关概念是解决此题的关键．
9．（3分）如图所示的长方形（长为14，宽为8）硬纸板，剪掉阴影部分后，将剩余的部分沿虚线折叠，制作成底面为正方形的长方体箱子，则长方体箱子的体积为（ ）
A．56B．40C．28D．20
【分析】观察图形，利用二元一次方程组求出底面正方形的边长和长方体的高，求出体积即可．
【解答】解：设长方体箱子的正方形底面的边长为a，长方体的高为b，
则：，
解得：，
∴体积为2×2×10＝40．
故选：B．
【点评】本题考查了认识立体图形，考查空间想象能力，利用二元一次方程组求出底面正方形的边长和长方体的高是解题的关键．
10．（3分）如图是一个运算程序，若输入﹣1，按如图所示的程序运算（完成一个方框内的运算后，把结果输入下一个方框继续进行运算），则输出的结果为（ ）
A．3B．﹣5C．0D．5
【分析】把相应的值代入运算，从而可求解．
【解答】解：当输入﹣1时，得：
﹣1+4﹣（﹣3）﹣5
＝﹣1+4+3﹣5
＝1，
当输入1时，得：
1+4﹣（﹣3）﹣5
＝1+4+3﹣5
＝3，
故选：A．
【点评】本题主要考查有理数的混合运算，解答的关键是对相应的运算法则的掌握．
二.填空题（每小题3分，共15分）
11．（3分）计算：1﹣2＝ ﹣1 ．
【分析】本题是对有理数减法的考查，减去一个数等于加上这个数的相反数．
【解答】解：1﹣2＝1+（﹣2）＝﹣1．
【点评】有理数的减法法则：减去一个数等于加上这个数的相反数．
12．（3分）如图，这是一个礼品盒，这个礼品盒有 12 条棱．
【分析】根据礼品盒是四棱柱，即可求出棱数．
【解答】解：礼品盒是四棱柱，有12条棱．
故答案为：12．
【点评】此题主要考查了认识立体图形，关键是结合实物，认识常见的立体图形，如：长方体、正方体、圆柱、圆锥、球、棱柱、棱锥等．能区分立体图形与平面图形，立体图形占有一定空间，各部分不都在同一平面内．
13．（3分）某天最高气温为6℃，最低气温为﹣3℃．这天的温差是 9 ℃．
【分析】用最高气温减去最低气温，然后根据减去一个数等于加上这个数的相反数进行计算即可得解．
【解答】解：6﹣（﹣3）＝6+3＝9（℃）．
故答案为：9．
【点评】本题考查了有理数的减法，熟记减去一个数等于加上这个数的相反数是解题的关键．
14．（3分）用一个平面去截一个三棱柱，截面图形的边数最多的为 五 边形．
【分析】方法：用平面去截几何体，平面与几何体几个面相加，就产生几条交线，就形成几边形，三棱柱只有五个面，最多截面与五个面相交，产生五条交线，形成五边形．
【解答】解：用一个平面去截一个三棱柱，截面图形的边数最多的为五边形．
故答案为：五．
【点评】本题考查了截一个几何体的知识，解决本题的关键是理解截面经过三棱柱的几个面，得到的截面形状就是几边形；经过截面相同，经过位置不同，得到的形状也不相同．注意：几何体的命名应用大写汉字，不能用阿拉伯数字．
15．（3分）已知|a|＝1，|b|＝2，|c|＝3，且b＞a＞c，则a+b+c的值为 ﹣2或0 ．
【分析】根据绝对值的意义，以及b＞a＞c，求出a，b，c的值，再把a，b，c的值代入所求代数式，求出a+b+c的值即可．
【解答】解：∵|a|＝1，|b|＝2，|c|＝3，
∴a＝±1，b＝±2，c＝±3，
∵b＞a＞c，
∴b＝2，a＝±1，c＝﹣3，
当b＝2，a＝﹣1，c＝﹣3时，
a+b+c＝﹣1+2﹣3＝﹣2；
当b＝2，a＝1，c＝﹣3时，
a+b+c＝1+2﹣3＝0；
综上：a+b+c的值为﹣2或0；
故答案为：﹣2或0．
【点评】本题主要考查了代数式求值．熟练掌握绝对值的意义，有理数的大小比较，正确的求出a，b，c的值，是解题的关键．
三、解答题（本题共8个小题，共75分）
16．（10分）（1）计算：20+（﹣14）﹣（﹣18）﹣|﹣13|．
（2）在计算“”时．甲同学的做法如下：
在甲同学的计算过程中，开始出错的步骤是 ① （写出错误所在行的序号），请你写出正确的计算过程．
【分析】（1）去括号，去绝对值，再进行加减运算即可；
（2）利用结合律进行简便运算．
【解答】解：（1）原式＝20﹣14+18﹣13
＝11；
（2）加括号时，后面一项没有变号，所以开始出错的步骤是①，
正确的计算过程如下：
＝15﹣8＝7．
【点评】本题考查有理数的加减运算．熟练掌握有理数的加减运算法则，是解题的关键．
17．（9分）在数轴上表示下列各数：，﹣3.5，﹣1.6，﹣，﹣4，2.5．并用“＜”把这些数连接起来．
【分析】先在数轴上表示出各个数，再根据有理数的大小比较法则比较大小即可．
【解答】解：如图所示：
﹣4＜﹣3.5＜﹣1.6＜﹣＜2.5．
【点评】本题考查了有理数的大小比较法则和数轴，能熟记有理数的大小比较法则是解此题的关键，注意：在数轴上表示的数，右边的数总比左边的数大．
18．（9分）如图，这是由8个大小相同的小立方块搭建的几何体，请按要求在方格内分别画出从这个几何体的三个不同方向看到的形状图．
【分析】根据三视图的定义画出图形即可．
【解答】解：三视图如图所示：
【点评】本题考查作图﹣三视图，解题的关键是掌握三视图的定义，属于中考常考题型．
19．（9分）（1）如图，下面两个图分别表示负数集合和分数集合，请你把下列各数填入它所在数集的圈里．
3.5，﹣25%，0，，﹣5，3，﹣2，．
（2）在（1）图中两个圈的重叠部分表示 负分 数的集合．
（3）列式并计算：在（1）的数据中，求最大的数与最小的数的和．
【分析】（1）根据负数和分数的定义分类即可；
（2）两个圈重叠的部分表示负分数集合；
（3）最大的数为3.5，最小的数为﹣5，计算即可．
【解答】解：（1）根据题意可得：
（2）这两个圈的重叠部分表示负分数集合；
故答案为：负分；
（3）∵在（1）的数据中，最大的数为3.5，最小的数为﹣5，∴3.5+（﹣5）＝﹣1.5．
【点评】本题考查有理数的运算和有理数的分类；熟练掌握有理数的分类，并能准确对有理数的加减法进行运算是解题的关键．
20．（9分）请根据图示的对话解答下列问题．
（1）分别求出a和b的值．
（2）已知|m﹣a|+|b+n|＝0，求m﹣n的值．
【分析】（1）根据相反数和绝对值的定义可得结果；
（2）根据绝对值的非负数性质解答即可．
【解答】解：（1）因为2的相反数是﹣2，所以a＝﹣2；
因为b＜a，且b的绝对值是﹣5，所以b＝﹣5；
（2）由题意得：
|m﹣（﹣2）|+|﹣5+n|＝0，
∴m+2＝0，﹣5+n＝0，
解得m＝﹣2，n＝5，
∴m﹣n＝﹣2﹣5＝﹣7．
【点评】本题考查了相反数的概念、非负数的性质：几个非负数的和为0时，这几个非负数都为0．
21．（9分）郑州到南阳有一列高铁从起点郑州东站经过新郑机场，郑州航空港，郑县，方城站到达终点南阳东站，一路上下乘客人数如表所示．（用正数表示上车的人数，负数表示下车的人数）
（1）问到南阳东站下车的有多少人？
（2）问高铁行驶在哪两站之间车上的乘客最多？
【分析】（1）将表格中的所有数据相加，和即为所求；
（2）分别求出从起点到终点，每两站之间车上的人数，比较大小后，即可得解．
【解答】解：（1）18+16+10+7+5+（﹣3）+（﹣5）+（﹣10）+（﹣14）＝24；
答：到南阳东站下车的有24人；
（2）从郑州东到新郑机场车上的人数为：18人；
从新郑机场到郑州航空港车上的人数为：18+16﹣3＝31人；
从郑州航空港到郑县车上的人数为：31+10﹣5＝36人；
从郑县到方城车上的人数为：36+7﹣10＝33人；
从方城到南阳东车上的人数为：33+5﹣14＝24人；
∵36＞33＞31＞24＞18，
∴高铁行驶在郑州航空港到郑县两站点间车上的人数最多．
【点评】本题考查正负数的意义，有理数的加法的实际应用．正确的理解题意，列出算式，是解题的关键．
22．（10分）【问题情境】
小圣所在的综合实践小组准备制作一些无盖纸盒收纳班级讲台上的粉笔．
【操作探究】
（1）图1中的哪些图形经过折叠能围成无盖正方体纸盒？ ①③④ （填序号）．
（2）小圣所在的综合实践小组把折叠成6个棱长都为2dm的无盖正方体纸盒摆成如图2所示的几何体．
①请计算出这个几何体的体积；
②如果在这个几何体上再添加一些相同的正方体纸盒，并保持从上面看到的形状和从左面看到的形状不变，最多可以再添加 3 个正方体纸盒．
【分析】（1）根据要求动手操作可得结论；
（2）①几何体有6个小正方体组成，由此可得结论；
②根据要求作出判断即可．
【解答】解：（1）①③④能围成无盖的正方体．
故答案为：①③④；
（2）①这个几何体的体积＝2×2×2×6＝48；
②如果在这个几何体上再添加一些相同的正方体纸盒，并保持从上面看到的形状和从左面看到的形状不变，最多可以再添加3个正方体．
故答案为：3．
【点评】本题考查简单组合体，展开图折叠成几何体等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
23．（10分）如图，甲、乙两人（看成点）分别在数轴﹣6和9的位置上，沿数轴做移动游戏．移动游戏规则；两人先进行“石头，剪刀、布”，而后根据输赢结果进行移动．
①若平局，则甲向东移动1个单位长度，同时乙向西移动1个单位长度；
②若甲赢，则甲向东移动5个单位长度，同时乙向东移动3个单位长度；
③若乙赢，则甲向西移动3个单位长度，同时乙向西移动5个单位长度．
前三局如表：（提示：剪刀胜布，布胜石头，石头胜剪刀）
（1）从如图所示的位置开始，求第一局后甲、乙两人分别在数轴上的位置．
（2）从如图所示的位置开始，从前三局看，第几局后甲离原点最近，离原点距离多少？
（3）从如图所示的位置开始，若进行了k局后，甲与乙的位置相距3个单位长度，请直接写出k的值．
【分析】（1）利用规则：若平局，则甲向东移动1个单位长度，同时乙向西移动1个单位长度，即可得结论；
（2）利用规则进行计算便可；
（3）由题意可得刚开始两人的距离为15，根据三种情况下计算出缩小的距离，即可算出缩小的总距离，分别除以2即可得到结果．
【解答】解：（1）完成了1次移动游戏，结果为平局，则甲向东移动1个单位长度到﹣5，乙向西移动1个单位长度到8；
（2）因为第二局甲赢，
所以甲向东移动5个单位长度，甲在数轴上的位置为0，
因为第三局乙赢，
所以甲向西移动3个单位长度，甲在数轴上的位置为﹣3，
所以从前三局看，第二局后甲离原点最近，离原点距离为0；
（3）k的值为6或9．
刚开始甲乙两人相距15个单位长度，
∵若平局，则甲向东移动1个单位长度，同时乙向西移动1个单位长度，
∴若平局，移动后甲乙的距离缩小2个单位．
∵若甲赢，则甲向东移动3个单位长度，同时乙向东移动1个单位长度，
∴若甲赢，移动后甲乙的距离缩小2个单位．
∵若乙赢，则甲向西移动1个单位长度，同时乙向西移动3个单位长度．
∴若乙赢，移动后甲乙的距离缩小2个单位．
∴甲乙每移动一次甲乙的距离缩小2个单位．
∵最终甲与乙的位置相距3个单位，共需缩小12个单位或18个单位．
∵12÷2＝6，18÷2＝9，
∴k的值为6或9．
【点评】本题主要考查了列代数式，数轴，本题是动点型题目，找出移动后甲乙距离变化的规律是解题的关键．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2024/9/3 8:24:26；用户：老师；邮箱：13937155109；学号：53598984
＝①
＝15﹣3②
＝12③
郑州东（起点）
新郑机场
郑州航空港
郑县
方城
南阳东（终点）
上车的人数
18
16
10
7
5
0
下车的人数
0
﹣3
﹣5
﹣10
﹣14
第一局
第二局
第三局
…
甲的手势
石头
剪刀
石头
…
乙的手势
石头
布
布
…
＝①
＝15﹣3②
＝12③
郑州东（起点）
新郑机场
郑州航空港
郑县
方城
南阳东（终点）
上车的人数
18
16
10
7
5
0
下车的人数
0
﹣3
﹣5
﹣10
﹣14
第一局
第二局
第三局
…
甲的手势
石头
剪刀
石头
…
乙的手势
石头
布
布
…