
2024-2025学年四川省遂宁市射洪中学九上数学开学达标检测模拟试题【含答案】
展开
这是一份2024-2025学年四川省遂宁市射洪中学九上数学开学达标检测模拟试题【含答案】,共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
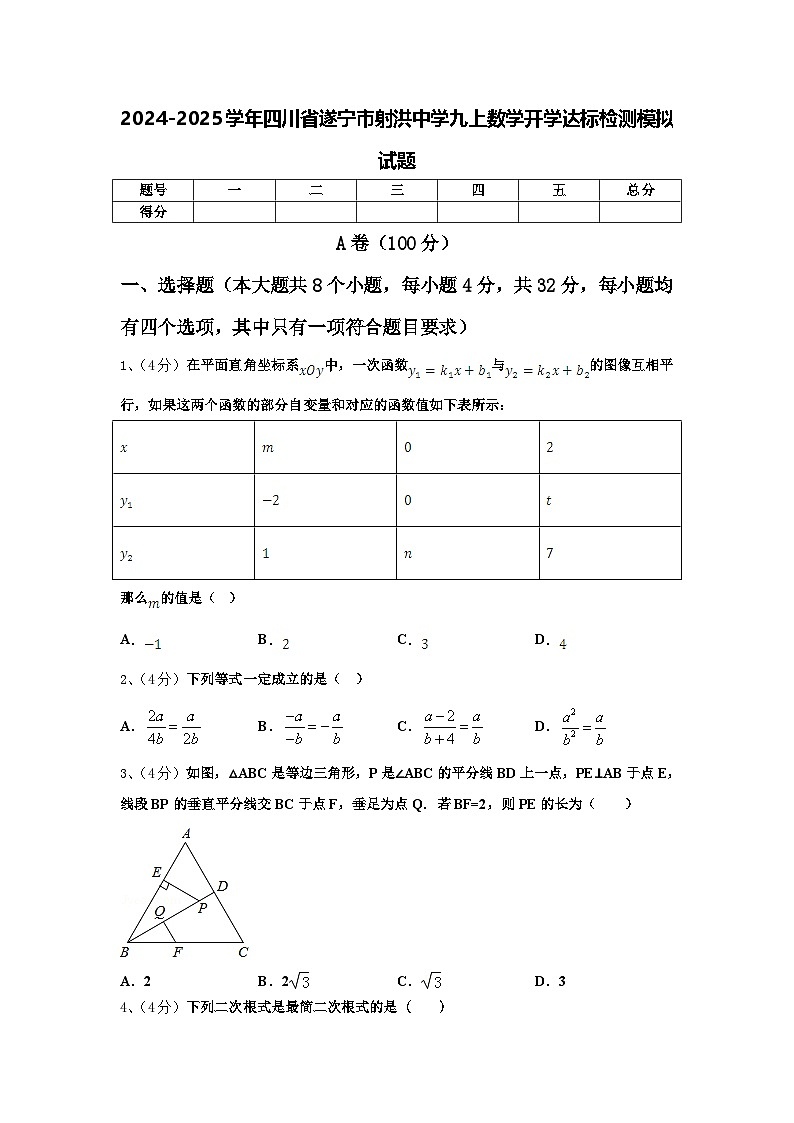
1、(4分)在平面直角坐标系中,一次函数与的图像互相平行,如果这两个函数的部分自变量和对应的函数值如下表所示:
那么的值是( )
A.B.C.D.
2、(4分)下列等式一定成立的是( )
A.B.C.D.
3、(4分)如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,则PE的长为( )
A.2B.2C.D.3
4、(4分)下列二次根式是最简二次根式的是( )
A.B.C.D.
5、(4分)如图,菱形中,分别是的中点,连接,则的周长为( )
A.B.C.D.
6、(4分)不等式6﹣4x≥3x﹣8的非负整数解为( )
A.2个B.3个C.4个D.5个
7、(4分)把分解因式,正确的是( )
A.B.C.D.
8、(4分)若等腰三角形的周长为18cm,其中一边长为4cm,则该等腰三角形的底边长为( )
A.10B.7或10C.4D.7或4
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)如图,菱形ABCD的对角线AC、BD相交于点O,E、F分别是AB、BC边的中点,连接EF,若EF=,BD=4,则菱形ABCD的边长为__________.
10、(4分)若已知方程组的解是,则直线y=-kx+b与直线y=x-a的交点坐标是________。
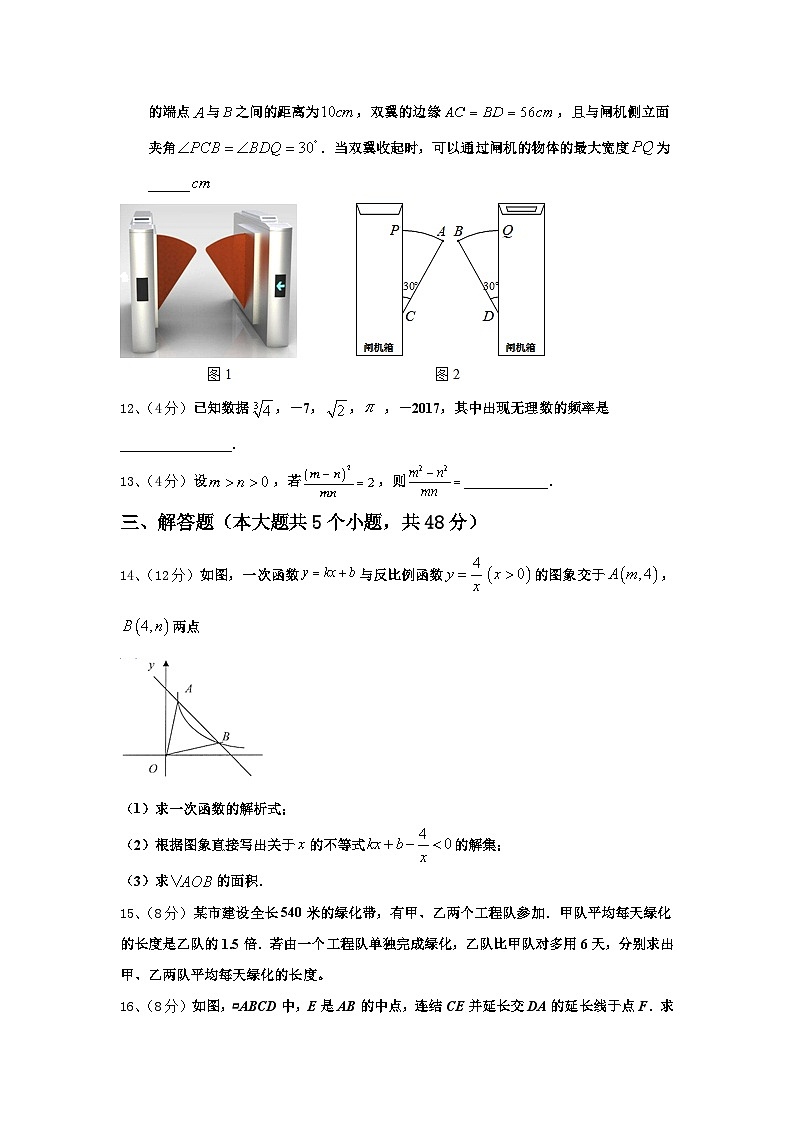
11、(4分)图1是一个地铁站人口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点与之间的距离为,双翼的边缘,且与闸机侧立面夹角.当双翼收起时,可以通过闸机的物体的最大宽度为______
12、(4分)已知数据,-7,, ,-2017,其中出现无理数的频率是________________.
13、(4分)设,若,则____________.
三、解答题(本大题共5个小题,共48分)
14、(12分)如图,一次函数与反比例函数的图象交于,两点
(1)求一次函数的解析式;
(2)根据图象直接写出关于的不等式的解集;
(3)求的面积.
15、(8分)某市建设全长540米的绿化带,有甲、乙两个工程队参加.甲队平均每天绿化的长度是乙队的1.5倍.若由一个工程队单独完成绿化,乙队比甲队对多用6天,分别求出甲、乙两队平均每天绿化的长度。
16、(8分)如图,▱ABCD中,E是AB的中点,连结CE并延长交DA的延长线于点F.求证:AFAD.
17、(10分)中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如图所示:
(1)统计表中的________,________,________;
(2)请将频数分布表直方图补充完整;
(3)求所有被调查学生课外阅读的平均本数;
(4)若该校八年级共有1200名学生,请你分析该校八年级学生课外阅读7本及以上的人数.
18、(10分)如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)如图,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2;以此下去…,则正方形A4B4C4D4的面积为_____.
20、(4分)为了解某小区居民的用水情况,随机抽查了20户家庭的月用水量,结果如下表:
则这组数据的中位数是_____.
21、(4分)若m+n=3,则2m2+4mn+2n2-6的值为________.
22、(4分)在中,,有一个锐角为,.若点在直线上(不与点、重合),且,则的长是___________
23、(4分)如图,矩形的边分别在轴、轴上,点的坐标为。点分别在边上,。沿直线将翻折,点落在点处。则点的坐标为__________。
二、解答题(本大题共3个小题,共30分)
24、(8分)如图,已知矩形ABCD中,点E是AB边上的一个动点,点F、G、H分别是CD、DE、CE的中点.
(1)求证:四边形EHFG是平行四边形;
(2)设AB=4,AD=3,求△EFG的面积.
25、(10分)如图,等腰直角中,,点在上,将绕顶点沿顺时针方向旋转90°后得到.
(1)求的度数;
(2)当,时,求的大小;
(3)当点在线段上运动时(不与,重合),求证:.
26、(12分)如图,将菱形OABC放置于平面直角坐标系中,边OA与x轴正半轴重合,D为边OC的中点,点E,F,G分别在边OA,AB与BC上,若∠COA=60°,OA=4,则当四边形DEFG为菱形时,点G的坐标为_____.
参考答案与详细解析
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、A
【解析】
由一次函数y2=k2x+b2与y2=k2x+b2的图象互相平行,得出k2=k2,设k2=k2=a,将(m,-2)、(0,0)代入y2=ax+b2,得到am=-2;将(m,2)、(0,n)、(2,7)代入y2=ax+b2,解方程组即可求出m的值.
【详解】
解:∵一次函数y2=k2x+b2与y2=k2x+b2的图象互相平行,
∴k2=k2,
设k2=k2=a,则y2=ax+b2,y2=ax+b2.
将(m,-2)、(0,0)代入y2=ax+b2,得am=-2①;
将(m,2)、(0,n)、(2,7)代入y2=ax+b2,
得am+n=2②,2a+n=7③,
①代入②,得n=3,
把n=3代入③,得a=2,
把a=2代入①,得m=-2.
故选:A.
本题考查了两条直线的平行问题:若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.即若直线y2=k2x+b2与直线y2=k2x+b2平行,那么k2=k2.也考查了一次函数图象上点的坐标特征.难度适中.
2、A
【解析】
根据分式的基本性质逐一判断即可.
【详解】
解:约分正确,故A正确,符号处理错误,故B错误,根据分式的基本性质明显错误,故C错误,根据分式的基本性质也错误,故D错误.
故选:A.
本题考查的是分式的基本性质对约分的要求,掌握分式的基本性质是解题关键.
3、C
【解析】
解析:∵△ABC是等边三角形P是∠ABC的平分线,
∴∠EBP=∠QBF=30°,
∵BF=2,FQ⊥BP,
∴BQ=BF•cs30°=2×=,
∵FQ是BP的垂直平分线,
∴BP=2BQ=2,
在Rt△BEF中,
∵∠EBP=30°,
∴PE=BP=.
故选C.
4、C
【解析】
【分析】最简二次根式: ① 被开方数不含有分母(小数);
② 被开方数中不含有可以开方开得出的因数或因式;
【详解】A. ,被开方数含有分母,本选项不能选;
B. ,被开方数中含有可以开方开得出的因数,本选项不能选;
C. 是最简二次根式;
D. ,被开方数中含有可以开方开得出的因数,本选项不能选.
故选:C
【点睛】本题考核知识点:最简二次根式.解题关键点:理解最简二次根式的条件.
5、D
【解析】
首先根据菱形的性质证明△ABE≌△ADF,然后连接AC可推出△ABC以及△ACD为等边三角形.根据等边三角形三线合一的性质又可推出△AEF是等边三角形.根据勾股定理可求出AE的长,继而求出周长.
【详解】
解:∵四边形ABCD是菱形,
∴AB=AD=BC=CD=2cm,∠B=∠D,
∵E、F分别是BC、CD的中点,
∴BE=DF,
在△ABE和△ADF中,,
∴△ABE≌△ADF(SAS),
∴AE=AF,∠BAE=∠DAF.
连接AC,
∵∠B=∠D=60°,
∴△ABC与△ACD是等边三角形,
∴AE⊥BC,AF⊥CD,
∴∠BAE=∠DAF=30°,
∴∠EAF=60°,BE=AB=1cm,
∴△AEF是等边三角形,AE=,
∴周长是.
故选:D.
本题主要考查了菱形的性质、全等三角形的判定和性质、等边三角形的判定和性质以及勾股定理,涉及知识点较多,也考察了学生推理计算的能力.
6、B
【解析】
移项得,﹣4x﹣3x≥﹣8﹣6,
合并同类项得,﹣7x≥﹣14,
系数化为1得,x≤1.
故其非负整数解为:0,1,1,共3个.
故选B.
7、A
【解析】
由提公因式法,提出公因式a,即可得到答案.
【详解】
解:,
故选择:A.
本题考查了提公因式法,解题的关键是正确找出公因式.
8、C
【解析】
根据等腰三角形性质分为两种情况解答:当边长4cm为腰或者4cm为底时
【详解】
当4cm是等腰三角形的腰时,则底边长18-8=10cm,此时4,4,10不能组成三角形,应舍去;当4cm是等腰三角形的底时,则腰长为(18-4)÷2=7cm,此时4,7,7能组成三角形,所以此时腰长为7,底边长为4,故选C
本题考查等腰三角形的性质与三角形三边的关系,本题关键在于分情况计算出之后需要利用三角形等边关系判断
二、填空题(本大题共5个小题,每小题4分,共20分)
9、
【解析】
先根据三角形中位线定理求AC的长,再由菱形的性质求出OA,OB的长,根据勾股定理求出AB的长即可.
【详解】
∵E、F分别是AB、BC边的中点,
∴EF是△ABC的中位线
∵EF=,
∴AC=2.
∵四边形ABCD是菱形,BD=4,
∴AC⊥BD,OA=AC=,OB=BD=2,
∴.
故答案为:.
此题考查菱形的性质、三角形中位线定理,解题关键在于熟练运用利用菱形的性质.
10、(-1,3)
【解析】
利用一次函数与二元一次方程组的关系,可知两一次函数的交点坐标就是两函数解析式所组成的方程组的解,可得结果.
【详解】
解:∵ 方程组 的解是 ,
∴直线y=kx−b与直线y=−x+a的交点坐标为(−1,3),
∴ 直线y=-kx+b与直线y=x-a的交点坐标为(-1,3).
故答案为:(-1,3)
本题考查了一次函数与二元一次方程(组):两一次函数的交点坐标是两函数解析式所组成的方程组的解.
11、
【解析】
过点A作AE⊥PC于点E,过点B作BF⊥QD于点F,根据含30度角的直角三角形的性质即可求出AE与BF的长度,然后求出EF的长度即可得出答案.
【详解】
解:过点A作AE⊥PC于点E,过点B作BF⊥QD于点F,
∵AC=56,∠PCA=30°,
由对称性可知:BF=AE,
∴通过闸机的物体最大宽度为2AE+AB=56+10=66;
故答案为:66cm.
本题考查解直角三角形,解题的关键是熟练运用含30度的直角直角三角形的性质,本题属于基础题型.
12、0.6
【解析】
用无理数的个数除以总个数即可.
【详解】
∵数据,-7,, ,-2017中无理数有, ,共3个,
∴出现无理数的频率是3÷5=0.6.
故答案为:0.6.
本题考查了无理数的定义,以及频率的计算,熟练运用频率公式计算是解题的关键.频率是指每个对象出现的次数与总次数的比值(或者百分比),即频率=频数÷总数
13、
【解析】
根据已知条件求出,,得到m-n与m+n,即可求出答案.
【详解】
∵,
∴,
∴,
∵m> n>0,
∴,,
∴,
故答案为:.
此题考查利用算术平方根的性质化简,平反差公式的运用,熟记公式是解题的关键.
三、解答题(本大题共5个小题,共48分)
14、(1);(2)或(3).
【解析】
(1)把A和B代入反比例函数解析式即可求得坐标,然后用待定系数法求得一次函数的解析式;
(2)不等式的解集就是:对于相同的x的值,反比例函数的图象在上边的部分自变量的取值范围;
(3)根据三角形的面积公式即可得到结论.
【详解】
(1)把,代入中,得,
∴,的坐标分别为,
把,代入中,得
解得
∴一次函数的表达式为
(2)根据图象得,不等式的解集为:或时.
(3)设一次函数与轴相交于点,
当时,
∴点的坐标为
∴
本题综合考查一次函数与反比例函数的图象与性质,同时考查用待定系数法求函数解析式.本题需要注意无论是自变量的取值范围还是函数值的取值范围,都应该从交点入手思考;需注意反比例函数的自变量不能取1.
15、甲队平均每天绿化45米,乙队平均每天绿化30米
【解析】
设乙队平均每天绿化x米, 由时间=工作量÷工作效率,结合乙队比甲队多用6天列分式方程,解出x, 再代入方程检验即可求出x, 则乙队平均每天绿化多少米也可求.
【详解】
设乙队平均每天绿化x米,则甲队平均每天绿化1.5x米,
依题意得
解得x=30
经检验x=30是原方程的根且符合题意,
∴1.5x=45(米),
答:甲队平均每天绿化45米,乙队平均每天绿化30米。
此题主要考查分式方程的应用,解题的关键是根据题意找到等量关系列方程.
16、详见解析.
【解析】
由在▱ABCD中,点E为AB的中点,易证得△AFE≌△BCE (ASA) ,然后由全等三角形的对应边相等得出AF=BC,即可证得结论.
【详解】
证明:∵平行四边形ABCD
∴AD∥BC,AD=BC (平行四边形对边平行且相等).
又∵AD∥BC
∴∠BCF=∠F(两直线平行内错角相等).
∠BAF=∠ABC
∵E为AB中点
在△AFE和△BCE中
∠BCF=∠F
∠BAF=∠ABC
AE=EB
∴△AFE≌△BCE (ASA)
∴AF=BC(全等三角形对应边相等)
∴AF=AD(等量代换)
此题考查全等三角形的判定与性质,平行四边形的性质,解题关键在于证明△AFE≌△BCE.
17、(1)10,0.28,50(2)图形见解析(3)6.4(4)528
【解析】
分析:(1)首先求出总人数,再根据频率,总数,频数的关系即可解决问题;
(2)根据a的值画出条形图即可;
(3)根据平均数的定义计算即可;
(4)用样本估计总体的思想解决问题即可;
详解:(1)由题意c==50,
a=50×0.2=10,b==0.28,c=50;
故答案为10,0.28,50;
(2)将频数分布表直方图补充完整,如图所示:
(3)所有被调查学生课外阅读的平均本数为:
(5×10+6×18+7×14+8×8)÷50=320÷50=6.4(本).
(4)该校七年级学生课外阅读7本及以上的人数为:
(0.28+0.16)×1200=528(人).
点睛:本题考查频数分布直方图、扇形统计图、样本估计总体等知识,解题的关键是熟练掌握基本概念,灵活运用所学知识解决问题,属于中考常考题型.
18、(1)(2,6);(2)作图见解析,点B'的坐标(0,-6);(3)(-7,3),(3,3),(-5,-3)
【解析】
(1)点B关于点A对称的点的坐标为(2,6);
(2)分别作出点A、B、C绕坐标原点O逆时针旋转90°后的点,然后顺次连接,并写出点B的对应点的坐标;
(3)分别以AB、BC、AC为对角线,写出第四个顶点D的坐标.
【详解】
解:(1)点B关于点A对称的点的坐标为(2,6);
(2)所作图形如图所示:
,
点B'的坐标为:(0,-6);
(3)当以AB为对角线时,点D坐标为(-7,3);
当以AC为对角线时,点D坐标为(3,3);
当以BC为对角线时,点D坐标为(-5,-3).
本题考查了根据旋转变换作图,轴对称的性质,以及平行四边形的性质,熟练掌握网格结构,准确找出对应点的位置是解题的关键.
一、填空题(本大题共5个小题,每小题4分,共20分)
19、1
【解析】
先求出每次延长后的面积,再发现规律即可求解.
【详解】
解:最初边长为1,面积1,
延长一次为,面积5,
再延长为51=5,面积52=25,
下一次延长为5,面积53=125,
以此类推,
当N=4时,正方形A4B4C4D4的面积为:54=1.
故答案为:1.
此题主要考查勾股定理的应用,解题的关键是根据题意找到规律进行求解.
20、5吨
【解析】
找中位数要把数据从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.
【详解】
表中数据为从小到大排列,吨处在第10位、第11位,为中位数,
故这组数据的中位数是吨.
故答案为:吨.
考查了中位数,将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.
21、1
【解析】
原式=2(m2+2mn+n2)-6,
=2(m+n)2-6,
=2×9-6,
=1.
22、或或
【解析】
分及两种情况:当时,由三角形内角和定理结合可得出为等边三角形,利用等边三角形的性质可求出的长;当时,通过解直角三角形可求出,的长,再由或可求出的长.综上,此题得解.
【详解】
解:I.当时,如图1所示.
,,
,
为等边三角形,
;
II.当时,如图2所示.
在中,,,
,.
在中,,
,
或.
故答案为12或或.
本题考查了含30度角的直角三角形、解直角三角形以及等边三角形的判定与性质,分及两种情况,求出的长是解题的关键.
23、
【解析】
由四边形OABC是矩形,BE=BD=1,易得△BED是等腰直角三角形,由折叠的性质,易得∠BEB′=∠BDB′=90°,又由点B的坐标为(3,2),即可求得点B′的坐标.
【详解】
∵四边形OABC是矩形,
∴∠B=90°,
∵BD=BE=1,
∴∠BED=∠BDE=45°,
∵沿直线DE将△BDE翻折,点B落在点B′处,
∴∠B′ED=∠BED=45°,∠B′DE=∠BDE=45°,B′E=BE=1,B′D=BD=1,
∴∠BEB′=∠BDB′=90°,
∵点B的坐标为(3,2),
∴点B′的坐标为(2,1).
故答案为:(2,1).
此题考查翻折变换(折叠问题),坐标与图形性质,解题关键在于得到△BED是等腰直角三角形
二、解答题(本大题共3个小题,共30分)
24、(1)见解析;(2)S△FEG=.
【解析】
(1)根据三角形的中位线定理求出FH∥DE,FG∥CE,根据平行四边形的判定求出即可;
(2)根据中线分三角形的面积为相等的两部分求解即可.
【详解】
(1)证明:因为点F、G、H分别是CD、DE、CE的中点,
所以,FH∥GE,FG∥EH,
所以,四边形EHFG是平行四边形;
(2)因为F为CD的中点,
所以DF=CD=AB=2,
因为G为DE的中点,所以,S△FDG=S△FEG,
所以,S△FEG=S△EFD=.
本题考查了矩形的性质,三角形的面积,平行四边形的判定等知识点,能正确运用等底等高的三角形的面积相等进行计算是解此题的关键.
25、(1);(1);(3)见解析.
【解析】
(1)由于∠PCB=∠BCQ=45°,故有∠PCQ=90°;
(1)利用勾股定理得出AC的长,再利用旋转的性质得出AP=CQ,求得PC的长度,进而利用勾股定理得出PQ的长;
(3)先证明△PBQ也是等腰直角三角形,从而得到PQ1=1PB1=PA1+PC1.
【详解】
(1)∵△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ,
∴,
∴,
∴.
(1)当时,有,,
,
∴.
(3)由(1)可得,,,
,
∴是等腰直角三角形,是直角三角形.
∴,
∵,
∴,
故有.
考查了旋转的性质以及勾股定理和等腰直角三角形的性质等知识,得出旋转前后对应线段之间关系是解题关键.
26、(3,2 )
【解析】
作辅助线,构建全等三角形,证明,得,由中点得,根据直角三角形30度角的性质和勾股定理得:,,所以,证明,根据菱形的对角线互相垂直平分得:的长,从而得的长,可得结论.
【详解】
解:过作于,交的延长线于,连接、,交于点,
四边形是菱形,
,
,
,,
,
,
,
,
中,,
,
,,
,
四边形是菱形,
,,,
,
,
,,
四边形为矩形,
,,
,,,
,
,
四边形是平行四边形,
,
,
,
,,
故答案为:,.
本题考查坐标与图形的性质、菱形的性质、全等三角形的判定和性质、平行四边形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.
题号
一
二
三
四
五
总分
得分
本数(本)
频数(人数)
频率
5
0.2
6
18
0.36
7
14
8
8
0.16
合计
1
月用水量/吨
4
5
6
8
户数
5
7
5
3
相关试卷
这是一份2024-2025学年四川省江油市六校九上数学开学达标检测模拟试题【含答案】,共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2024-2025学年四川省成都市师大一中学九上数学开学达标检测模拟试题【含答案】,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2024-2025学年陕西省西安工业大附属中学数学九上开学达标检测模拟试题【含答案】,共25页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








