2024-2025学年四川省资阳安岳县联考数学九上开学质量检测模拟试题【含答案】

这是一份2024-2025学年四川省资阳安岳县联考数学九上开学质量检测模拟试题【含答案】，共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）在平面直角坐标系中，将正比例函数（＞0）的图象向上平移一个单位长度，那么平移后的图象不经过（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
2、（4分）如图，在平行四边形ABCD中，BC＝10，AC＝14，BD＝8，则△BOC的周长是( )
A．21B．22C．25D．32
3、（4分）如图是我市某一天内的气温变化图，根据图象，下列说法中错误的是( )
A．这一天中最高气温是26℃
B．这一天中最高气温与最低气温的差为16℃
C．这一天中2时至14时之间的气温在逐渐升高
D．这一天中14时至24时之间的气温在逐渐降低
4、（4分）化简的结果是（ ）
A．2B．-4C．4D．±4
5、（4分）如图，△A1B1C1是由△ABC沿BC方向平移了BC长度的一半得到的，若△ABC的面积为20cm2，则四边形A1DCC1的面积为（ ）
A．10 cm2B．12 cm2C．15 cm2D．17 cm2
6、（4分）下列命题是真命题的是（ ）
A．四边都是相等的四边形是矩形B．菱形的对角线相等
C．对角线互相垂直的平行四边形是正方形D．对角线相等的平行四边形是矩形
7、（4分）下列化简正确的是（ ）
A．B．C．D．
8、（4分）下列命题正确的是（ ）
A．两条对角线互相平分且相等的四边形是菱形
B．两条对角线互相平分且垂直的四边形是矩形
C．两条对角线互相垂直且相等的四边形是正方形
D．角平分线上的点到角两边的距离相等
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）关于x的方程（m﹣2）x2+2x+1＝0有实数根，则偶数m的最大值为_____．
10、（4分）写出一个图象经过一，三象限的正比例函数y=kx（k≠0）的解析式（关系式） ．
11、（4分）某公司招聘一名公关人员甲，对甲进行了笔试和面试，其面试和笔试的成绩分别为86分和90分，面试成绩和笔试成绩的权分别是6和4，则甲的平均成绩为__分．
12、（4分）将直线向上平移3个单位长度与直线重合，则直线的解析式为__________．
13、（4分）已知点P(-2,1)，则点P关于x轴对称的点的坐标是__．
三、解答题（本大题共5个小题，共48分）
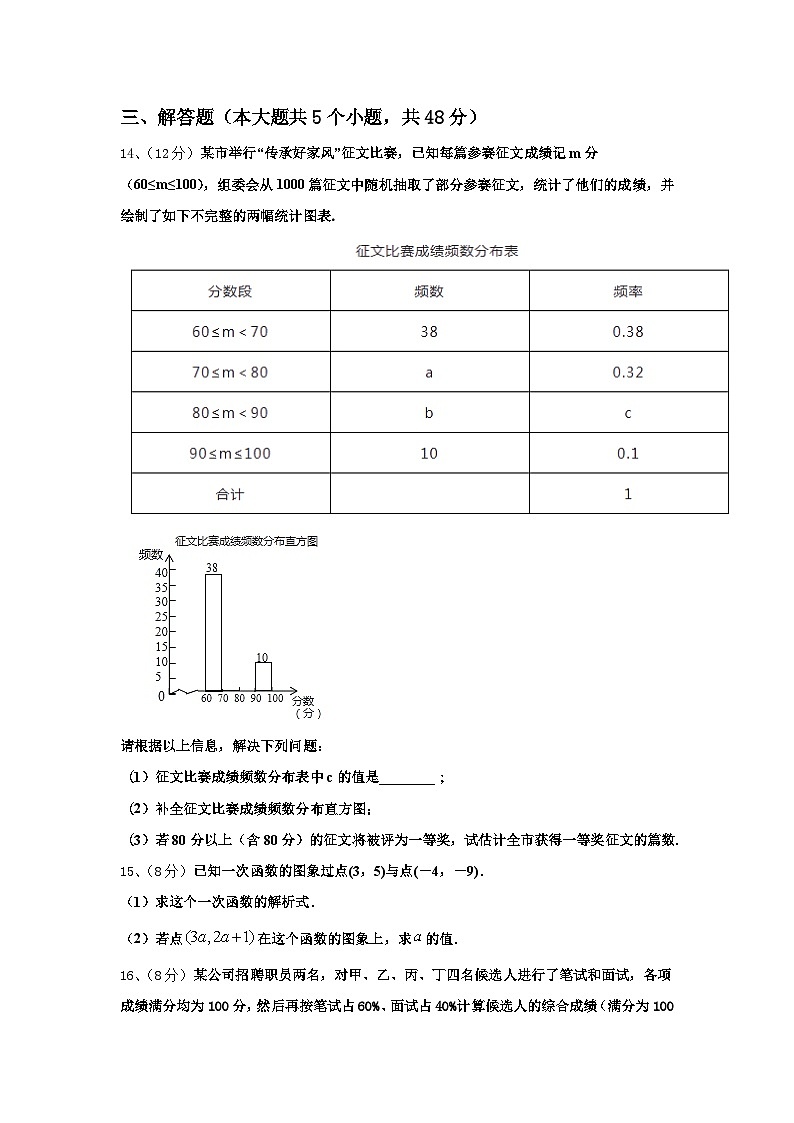
14、（12分）某市举行“传承好家风”征文比赛，已知每篇参赛征文成绩记m分（60≤m≤100），组委会从1000篇征文中随机抽取了部分参赛征文，统计了他们的成绩，并绘制了如下不完整的两幅统计图表.

请根据以上信息，解决下列问题：
（1）征文比赛成绩频数分布表中c的值是________；
（2）补全征文比赛成绩频数分布直方图；
（3）若80分以上（含80分）的征文将被评为一等奖，试估计全市获得一等奖征文的篇数.
15、（8分）已知一次函数的图象过点(3，5)与点(－4，－9)．
（1）求这个一次函数的解析式．
（2）若点在这个函数的图象上，求的值．
16、（8分）某公司招聘职员两名，对甲、乙、丙、丁四名候选人进行了笔试和面试，各项成绩满分均为100分，然后再按笔试占60%、面试占40%计算候选人的综合成绩（满分为100分）．
他们的各项成绩如下表所示：
（1）直接写出这四名候选人面试成绩的中位数；
（2）现得知候选人丙的综合成绩为87.6分，求表中x的值；
（3）求出其余三名候选人的综合成绩，并以综合成绩排序确定所要招聘的前两名的人选．
17、（10分）（1）已知一组数据8,3,m,2的众数是3，求出这组数据的平均数；
（2）解方程：.
18、（10分）某学校计划购买若干台电脑，现从两家商场了解到同一种型号的电脑报价均为6000元，并且多买都有一定的优惠.各商场的优惠条件如下表所示：
(1)设学校购买台电脑，选择甲商场时，所需费用为元，选择乙商场时，所需费用为元，请分别求出，与之间的关系式.
(2)什么情况下，两家商场的收费相同？什么情况下，到甲商场购买更优惠？什么情况下，到乙商场购买更优惠？
(3)现在因为急需，计划从甲乙两商场一共买入10台电脑，已知甲商场的运费为每台50元，乙商场的运费为每台60元，设总运费为元，从甲商场购买台电脑，在甲商场的库存只有4台的情况下，怎样购买，总运费最少？最少运费是多少？
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，在▱ABCD中，分别设P，Q，E，F为边AB，BC，AD，CD的中点，设T为线段EF的三等分点，则△PQT与▱ABCD的面积之比是______．
20、（4分）如图，在平行四边形纸片中，，将纸片沿对角线对折，边与边交于点，此时恰为等边三角形，则重叠部分的面积为_________．
21、（4分）如图，在平行四边形ABCD中，对角线AC与BD相交于点O，点E为BC边的中点，连接OE，若AB＝4，则线段OE的长为_____．
22、（4分）将直线向上平移一个单位长度得到的一次函数的解析式为_______________.
23、（4分）如图所示，将△ABC绕AC的中点O顺时针旋转180°得到△CDA，添加一个条件_____，使四边形ABCD为矩形．
二、解答题（本大题共3个小题，共30分）
24、（8分）（如图①，将边长为4cm的正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点 M处，点C落在点N处，MN与CD交于点P， 连接EP．
⑴如图②，若M为AD边的中点，①△AEM的周长=_________cm；②求证：EP=AE+DP；
⑵随着落点M在AD边上取遍所有的位置(点M不与A、D重合)，△PDM的周长是否发生变化?请说明理由．
25、（10分）如图，已知各顶点的坐标分别为，，．
（1）画出以点B为旋转中心，按顺时针方向旋转后得到的；
（2）将先向右平移5个单位长度，再向上平移3个单位长度，得到．
①在图中画出，并写出点A的对应点的坐标；
②如果将看成是由经过一次平移得到的，请指出这一平移的平移方向和平移距离．
26、（12分）物理兴趣小组20位同学在实验操作中的得分情况如下表：
问：（1）求这20位同学实验操作得分的众数、中位数．
（2）这20位同学实验操作得分的平均分是多少？
（3）将此次操作得分按人数制成如图所示的扇形统计图，扇形①的圆心角度数是多少？
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
试题分析：将正比例函数y=kx（k＞0）的图象向上平移一个单位得到y=kx+1（k＞0），
∵k＞0，b=1＞0，
∴图象经过第一、二、三象限，不经过第四象限．
故选D．
考点：一次函数图象与几何变换．
2、A
【解析】
由平行四边形的性质得出OA＝OC＝7，OB＝OD＝4，即可得出△BOC的周长．
【详解】
解：∵四边形ABCD是平行四边形，
∴OA＝OC＝7，OB＝OD＝4，
∴△BOC的周长＝OB+OC+BC＝4+7+10＝21；
故选：A．
本题考查了平行四边形的性质以及三角形周长的计算；熟记平行四边形的对角线互相平分是解题关键．
3、A
【解析】
根据函数图象的纵坐标，可得气温，根据函数图象的增减性，可得答案．
【详解】
A、由纵坐标看出，这一天中最高气温是24℃，错误，故A符合选项；
B、由纵坐标看出最高气温是24℃，最低气温是8℃，温差是24﹣8＝16℃，正确，故B不符合选项；
C、由函数图象看出，这一天中2时至14时之间的气温在逐渐升高，故C正确；
D、由函数图象看出，这一天中0时至2时，14时至24时气温在逐渐降低，故D错误；
故选：A．
考查了函数图象，由纵坐标看出气温，横坐标看出时间是解题关键．
4、C
【解析】
根据算术平方根的性质直接进行计算即可．
【详解】
=|-1|=1．
故选：C．
本题考查的是算术平方根的定义，把化为|-1|的形式是解答此题的关键．
5、C
【解析】
解：∵△A1B1C1是由ABC沿BC方向平移了BC长度的一半得到的，
∴AC∥AC1，B1C=B1C1，
∴△B1DC∽△B1A1C1，
∵△B1DC与△B1A1C1的面积比为1：4，
∴四边形A1DCC1的面积是△ABC的面积的，
∴四边形A1DCC1的面积是：cm2，
故选C
6、D
【解析】
根据矩形的判定定理，菱形的性质，正方形的判定判断即可得到结论．
【详解】
A、四边都相等的四边形是菱形，故错误；
B、矩形的对角线相等，故错误；
C、对角线互相垂直的平行四边形是菱形，故错误；
D、对角线相等的平行四边形是矩形，正确，
故选D．
熟练掌握特殊平行四边形的各自特点，矩形对角线相等，邻边垂直．菱形对角线垂直且平分对角，邻边相等．同时具备矩形和菱形的四边形是正方形．
7、A
【解析】
根据二次根式的性质以及合并同类二次根式法则，一一化简即可．
【详解】
A. 正确.
B. 错误.
C. 错误.
D. 错误. .
故选A.
此题考查二次根式的加减法，二次根式的性质与化简，解题关键在于掌握运算法则.
8、D
【解析】
根据菱形、矩形、正方形的判定和角平分线的性质判断即可．
【详解】
解：、两条对角线互相平分且垂直的四边形是菱形，故选项是假命题；
、两条对角线互相平分且相等的四边形是矩形，故选项是假命题；
、两条对角线互相平分且垂直且相等的四边形是正方形，故选项是假命题；
、角平分线上的点到角两边的距离相等，故选项是真命题；
故选：．
本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果那么”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1
【解析】
由方程有实数根，可得出b1﹣4ac≥0，代入数据即可得出关于m的一元一次不等式，解不等式即可得m的取值范围，再找出其内的最大偶数即可．
【详解】
解：当m﹣1＝0时，原方程为1x+1＝0，
解得：x＝﹣，
∴m＝1符合题意；
当m﹣1≠0时，△＝b1﹣4ac＝11﹣4（m﹣1）≥0，
即11﹣4m≥0，
解得：m≤3且m≠1．
综上所述：m≤3，
∴偶数m的最大值为1．
故答案为：1．
本题考查了根的判别式以及解一元一次方程，分方程为一元一次或一元二次方程两种情况找出m的取值范围是解题的关键．
10、y=2x
【解析】
试题分析：根据正比例函数y=kx的图象经过一，三象限，可得k＞0，写一个符合条件的数即可．
解：∵正比例函数y=kx的图象经过一，三象限，
∴k＞0，
取k=2可得函数关系式y=2x．
故答案为y=2x．
点评：此题主要考查了正比例函数的性质，关键是掌握正比例函数图象的性质：它是经过原点的一条直线．当k＞0时，图象经过一、三象限，y随x的增大而增大；当k＜0时，图象经过二、四象限，y随x的增大而减小．
11、87.1．
【解析】
根据加权平均数的含义和求法，可求出甲的平均成绩.
【详解】
面试和笔试的成绩分别为81分和90分，面试成绩和笔试成绩的权分别是1和4，
甲的平均成绩为：（分）．
故答案为：87.1．
考查加权平均数的计算，掌握加权平均数的计算方法是解题的关键.
12、
【解析】
根据一次函数的平移规律：左加右减，上加下减，即可求出原直线的解析式．
【详解】
解：∵直线向上平移3个单位长度与直线重合，
∴直线向下平移3个单位长度与直线重合
∴直线的解析式为：
故答案为：．
此题考查的是根据平移后的一次函数解析式，求原直线的解析式，掌握一次函数的平移规律：左加右减，上加下减，是解决此题的关键．
13、 (-2,-1)
【解析】
根据关于x轴对称的点的横坐标相等，纵坐标互为相反数，可得答案．
【详解】
点P（﹣2，1），则点P关于x轴对称的点的坐标是（﹣2，﹣1），
故答案是：（﹣2，﹣1）．
考查了关于x轴对称的对称点，利用关于x轴对称的点的横坐标相等，纵坐标互为相反数是解题关键．
三、解答题（本大题共5个小题，共48分）
14、（1）0.2；（2）补全征文比赛成绩频数分布直方图见解析；（3）全市获得一等奖征文的篇数为300篇.
【解析】
【分析】（1）由频率之和为1，用1减去其余各组的频率即可求得c的值；
（2）由频数分布表可知 60≤m＜70的频数为：38，频率为：0.38，根据总数=频数÷频率得样本容量，再由频数=总数×频率求出a、b的值，根据a、b的值补全图形即可；
（3）由频数分布表可知评为一等奖的频率为：0.2+0.1=0.3，再用总篇数×一等奖的频率=全市一等奖征文篇数.
【详解】（1）c=1-0.38-0.32-0.1=0.2，
故答案为：0.2；
（2）38÷0.38=100，a=100×0.32=32，b=100×0.2=20，
补全征文比赛成绩频数分布直方图如图所示：
（3）由频数分布表可知评为一等奖的频率为：0.2+0.1=0.3，
∴全市获得一等奖征文的篇数为：1000×0.3=300（篇），
答：全市获得一等奖征文的篇数为300篇.
【点睛】本题考查了频数分布表、频数分布直方图，熟知频数、频率、总数之间的关系是解本题的关键.
15、（1）；（2）
【解析】
（1）设函数解析式为，将两点坐标代入求解即可；
（2）将点的坐标代入解析式即可求的值．
【详解】
（1）设函数解析式为，将两点坐标代入得
，
解之得，
所求的解析式为
（2）将点的坐标代入上述解析式得
，
解之得
本题考查了一次函数的问题，掌握一次函数的性质以及应用是解题的关键．
16、（1）这四名候选人面试成绩的中位数为89（分）；（2）表中x的值为86；（3）以综合成绩排序确定所要招聘的前两名的人选是甲和丙．
【解析】
（1）根据中位数的概念计算；
（2）根据题意列出方程，解方程即可；
（3）根据加权平均数的计算公式分别求出余三名候选人的综合成绩，比较即可．
【详解】
（1）这四名候选人面试成绩的中位数为：=89（分）；
（2）由题意得，x×60%+90×40%=87.6
解得，x=86，
答：表中x的值为86；
（3）甲候选人的综合成绩为：90×60%+88×40%=89.2（分），
乙候选人的综合成绩为：84×60%+92×40%=87.2（分），
丁候选人的综合成绩为：88×60%+86×40%=87.2（分），
∴以综合成绩排序确定所要招聘的前两名的人选是甲和丙．
本题考查的是中位线、加权平均数，掌握中位数的概念、加权平均数的计算公式是解题的关键．
17、（1）4；（2）.
【解析】
（1）根据众数的定义求出m,即可求出平均数；
（2）根据因式分解求解即可.
【详解】
（1）解：∵一组数据8，3，，2的众数为3，
∴，
∴这组数据的平均数：．
（2）.
(x+3)（x+1）=0
．
本题考查的是平均数和解二次方程，熟练掌握众数和因式分解是解题的关键.
18、（1）y1=4500x+1500；y2=4800x；（2）答案见解析；（3）从甲商场买4台，从乙商场买6台时，总运费最少，最少运费是560元
【解析】
（1）根据题意列出函数解析式即可；
（2）①若甲商场购买更优惠，可得不等式4500x+1500＜4800x，解此不等式，即可求得答案；
②若乙商场购买更优惠，可得不等式4500x+1500＞4800x，解此不等式，即可求得答案；
③若两家商场收费相同，可得方程4500x+1500=4800x，解此方程，即可求得答案；
（3）根据题意列出函数解析式，再根据增减性即可进行解答．
【详解】
解：（1）y1=6000+（1-25%）×6000（x-1）=4500x+1500；
y2=（1-20%）×6000x=4800x；
（2）设学校购买x台电脑，
若到甲商场购买更优惠，则：
4500x+1500＜4800x，
解得：x＞5，
即当购买电脑台数大于5时，甲商场购买更优惠；
若到乙商场购买更优惠，则：
4500x+1500＞4800x，
解得：x＜5，
即当购买电脑台数小于5时，乙商场购买更优惠；
若两家商场收费相同，则：
4500x+1500=4800x，
解得：x=5，
即当购买5台时，两家商场的收费相同；
（3）w=50a+（10-a）60=600-10a，
当a取最大时，费用最小，
∵甲商场只有4台，
∴a取4，W=600-40=560，
即从甲商场买4台，从乙商场买6台时，总运费最少，最少运费是560元．
本题考查了一元一次不等式实际应用问题，涉及了不等式与方程的解法，解题的关键是理解题意，根据题意求得函数解析式，然后利用函数的性质求解．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1：1
【解析】
如图，连接AC、PE、QF．设平行四边形ABCD的面积为8S,证明四边形EFQP是平行四边形，求出S平行四边形EFQP＝1S和S△TPQ＝2S即可解决问题.
【详解】
解：如图，连接AC、PE、QF．设平行四边形ABCD的面积为8S．
∵DE＝AE，DF＝FC，
∴EF∥AC，EF：AC＝1：2，
∴S△DEF＝S△DAC＝×1S＝S，
同理可证PQ∥AC，PQ：AC＝1：2，S△CFQ＝S△PQB＝S△APE＝S，
∴四边形EFQP是平行四边形，
∴S平行四边形EFQP＝1S，
∴S△TPQ＝S平行四边形EFQP＝2S，
∴S△TPQ：S平行四边形ABCD＝2S：8S＝1：1，
故答案为1：1．
本题考查的是平行四边形的综合运用，熟练掌握平行四边形的性质和相似三角形的性质是解题的关键.
20、
【解析】
首先根据等边三角形的性质可得A B'=AE=E B'，∠B'=∠B'EA=60°，根据折叠的性质，∠BCA=∠B'CA，，再证明∠B'AC=90°，再证得S△AEC=S△AEB'，再求S△A B'C进而可得答案．
【详解】
解：∵为等边三角形，
∴A B'=AE=E B'，∠B'=∠B'EA=60°，
根据折叠的性质，∠BCA=∠B'CA，
∵四边形ABCD是平行四边形，
∴AD//BC，AD=BC，AB=CD，
∴∠B'EA=∠B'CB，∠EAC=∠BCA，
∴∠ECA=∠BCA=30°,
∴∠EAC=30°，
∴∠B'AC=90°，
∵,
∴B'C=8,
∴AC==,
∵B'E=AE=EC,
∴S△AEC=S△AEB'= S△A B'C= × ×4×=,
故答案为.
此题主要考查了平行四边形的性质、直角三角形的性质以及翻折变换，关键是掌握平行四边形的对边平行且相等，直角三角形30°角所对的边等于斜边的一半．
21、2
【解析】
证出OE是△ABC的中位线，由三角形中位线定理即可求得答案．
【详解】
解：∵四边形ABCD是平行四边形，
∴OA＝OC；
又∵点E是BC的中点，
∴OE是△ABC的中位线，
∴OE＝AB＝2，
故答案为：2．
此题考查了平行四边形的性质以及三角形中位线的定理；熟练掌握平行四边形的性质和三角形中位线定理是解题的关键．
22、
【解析】
解：由平移的规律知，得到的一次函数的解析式为.
23、∠B=90°．
【解析】
根据旋转的性质得AB=CD，∠BAC=∠DCA，则AB∥CD，得到四边形ABCD为平行四边形，根据有一个直角的平行四边形为矩形可添加的条件为∠B=90°．
【详解】
∵△ABC绕AC的中点O顺时针旋转180°得到△CDA，
∴AB=CD，∠BAC=∠DCA，
∴AB∥CD，
∴四边形ABCD为平行四边形，
当∠B=90°时，平行四边形ABCD为矩形，
∴添加的条件为∠B=90°．
故答案为∠B=90°．
本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了矩形的判定．
二、解答题（本大题共3个小题，共30分）
24、（1）①6 ，②见解析；（2）△PDM的周长保持不变，理由见解析.
【解析】
（1）①由折叠知BE=EM,AE+EM+AM=AE+EB+AM=AB+AM,根据边长及中点易求周长；②延长EM交CD延长线于Q点．可证△AEM≌△DQM，得AE=DQ，EM=MQ．所以PM垂直平分EQ，得EP=PQ，得证；
（2）不变化，可证△AEM∽△DMP，两个三角形的周长比为AE：MD，设AM=x，根据勾股定理可以用x表示MD的长与△MAE的周长，再根据周长比等于相似比，即可求解.
【详解】
（1）①由折叠可知，BE=BM,∠B=∠MEP=90°，
△AEM的周长= AE+EM+AM=AE+EB+AM=AB+AM.
∵AB=4，M是AD中点，
∴△AEM的周长=6（cm）
②证明：延长EM交CD延长线于Q点．
∵∠A=∠MDQ=90°，AM=DM，∠AME=∠DMQ，
∴△AME≌△DMQ．
∴AE=DQ，EM=MQ．
又∵∠EMP=∠B=90°，
∴PM垂直平分EQ，有EP=PQ．
∵PQ=PD+DQ，
∴EP=AE+PD．
(2)△PDM的周长保持不变，
证明：设AM=xcm，则DM=（4－x）cm ，
Rt△EAM中，由，
，
∵∠AME+∠AEM=90°，
∠AME+∠PMD=90°，
∴∠AEM=∠PMD，
又∵∠A=∠D=90°，
∴△PDM∽△MAE，
∴，
即，
∴，
∴△PDM的周长保持不变．
25、（1）详见解析；（2）①图详见解析，A2（2，-1）；②由A到A2的方向，平移的距离是个单位长度．
【解析】
（1）根据旋转的性质即可作图；（2）①根据平移的性质画出图形即可；②连接A A2，根据勾股定理求出A A2的长，进而可得出结论．
【详解】
（1）如图所示，即为所求；
（2）①如图所示，即为所求，A2（2，-1）；
②连接AA2，由勾股定理求得AA2= ，
∴如果将看成是由经过一次平移得到的，那么这一平移的平移方向是由A到A2的方向，平移的距离是个单位长度．
本题考查的是作图-旋转变换及平移变换，熟知图形平移不变性的性质是解答第（2）问的关键．
26、（1）众数：9，中位数：9；
（2）这20位同学实验操作得分的平均分为：；
（3）扇形①的圆心角度数是：（1-20%-25%-40%）×360°=54°．
【解析】
（1）得9分的有8人，频数最多；20个数据的中位数是第10个和第11个同学的得分的平均数；
（2）平均分=总分数÷总人数；
（3）扇形①的圆心角=百分比×360°
题号
一
二
三
四
五
总分
得分
修造人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
商场
优惠条件
甲商场
第一台按原价收费，其余的每台优惠25%
乙商场
每台优惠20%