高中数学人教A版 (2019)选择性必修 第三册6.2 排列与组合学案及答案

这是一份高中数学人教A版 (2019)选择性必修 第三册6.2 排列与组合学案及答案，共4页。学案主要包含了排列数与排列数公式，小结，作业等内容，欢迎下载使用。
学科素养：1.数学抽象，2.逻辑推理，3.数学运算，4.数学建模
重 点：熟练运用排列数公式进行计算，掌握有限制条件的排列应用题的一些常用方法
难 点：运用排列数公式解决计算问题
教学过程：
一、排列数与排列数公式
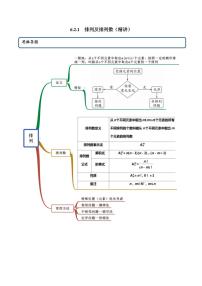
1、排列数的定义:从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数,叫做从n个不同元素中取出m个元素的排列数,用符号Anm表示.
2、排列数公式:Anm=n(n-1)(n-2)…(n-m+1)=n!(n-m)!,这里m,n∈N*,并且m≤n.
3、全排列和阶乘:n个不同元素全部取出的一个排列,叫做n个元素的一个全排列.这时,排列数公式中m=n,即有Ann=n(n-1)(n-2)×…×3×2×1.也就是说,将n个不同的元素全部取出的排列数,等于正整数1到n的连乘积.正整数1到n的连乘积,叫做n的阶乘,用n!表示.于是,n个元素的全排列数公式可以写成Ann=n!.另外,我们规定,0!=1.
问：你认为“排列”和“排列数”是同一个概念吗?它们有什么区别?
“排列”与“排列数”是两个不同的概念,一个排列是指“从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列”,它不是一个数,而是具体的一件事.“排列数”是指“从n个不同元素中取出m(m≤n)个元素的所有不同排列的个数”,它是一个数.
例题讲解：
（一）排列数计算：
（课本）计算：（1）A73；2A74；3A77A44；4A64×A22
练习：课本20页1、3
典例1、（1）已知，且，则用排列数表示为_______
练习：学导13页左上2
（二）与排列数有关的方程、不等式及证明：
典例2
计算：若，则______;
若________
解不等式
求证：
练习：课本20页2
数字的排列问题：
例4（课本）用0~9这10个数字，可以组成多少个没有重复数字的三位数？
典例5（学导）用0,1,2,3,4,5六个数字：
能组成多少个无重复数字的四位偶数；
能组成多少个无重复数字且为5的倍数的五位数；
能组成多少个无重复数字且比1325大的四位数
小结：1、排列数公式；2、数字排列问题
作业：配检（四）
课 题： 6.2.2排列数（2） 课型：
教学目标：掌握有限制条件的排列应用题的一些常用方法,并能运用排列的相关知识解一些简单的排列应用题.
学科素养：1.数学抽象，2.逻辑推理，3.数学运算，4.数学建模
重 点：掌握有限制条件的排列应用题的一些常用方法：捆绑法、插空法
难 点：掌握有限制条件的排列应用题的一些常用方法：捆绑法、插空法
教学过程：
复习回顾：
1、排列数公式:Anm=n(n-1)(n-2)…(n-m+1)=n!(n-m)!,这里m,n∈N*,并且m≤n.
2、Ann=n(n-1)(n-2)×…×3×2×1.
例题讲解：
练习排列数计算：
解不等式
有限制条件的排列问题：
典例4 3名男生，4名女生，按照下列不同的要求排队，求不同的站队方法总数。
全体站成一排，其中甲只能站在中间或两端；
全体站成一排，其中甲、乙只能站在两端；
全体站成一排，其中甲不能站在两端；
全体站成一排，甲不站最左端，乙不站最右端
全体站成一排，其中甲乙不能相邻；
全体站成一排，其中甲乙必须相邻.
练习：学导14页对点练1；15页2、3
三、小结：有限制条件的排列应用题的一些常用方法：捆绑法、插空法
四、作业：
1、整理学导11-15
补充：
有3名女生、4名男生站成一排，女生必须相邻，男生也必须相邻，则有多少种排法？
6个停车位，有三辆汽车需要停放，若要使3个空位连在一起，则停放的方法有多少种？
甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演，若甲不站在两端，丙和丁相邻，则不同的排列方法有几种？
某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序，则同类节目不相邻的排法有几种？
把5件不同产品摆成一排，若产品A与产品B相邻，且产品A与产品C不相邻，则不同的摆法有几种？