202-2025学年人教版数学九年级上册第一次月考 模拟试题

这是一份202-2025学年人教版数学九年级上册第一次月考 模拟试题，共13页。试卷主要包含了抛物线y＝3，函数y＝ax2﹣a等内容，欢迎下载使用。
学校:___________姓名：___________班级：___________考号：___________
一．选择题（共10小题，满分30分，每小题3分）
1．一元二次方程3x2﹣8x﹣10＝0的一次项系数为（ ）
A．8B．﹣8C．﹣10D．10
2．抛物线y＝3（x﹣2）2+1的对称轴是（ ）
A．直线x＝﹣2B．直线x＝﹣1C．直线x＝1D．直线x＝2
3．用配方法解方程x2+4x+2＝0时，配方结果正确的是（ ）
A．（x+2）2＝2B．（x﹣2）2＝2C．（x+2）2＝6D．（x﹣2）2＝6
4．将二次函数y＝x2﹣2x﹣3的图象先向右平移1个单位，再向上平移2个单位，得到的二次函数y1的图象，则函数y1的表达式是（ ）
A．y1＝x2﹣6B．y1＝x2﹣2
C．y1＝x2﹣4x﹣2D．y1＝x2﹣4x+2
5．一元二次方程x2﹣4x+3＝0的根的情况是（ ）
A．有两个相等的实数根 B．有两个不相等的实数根
C．只有一个实数根 D．没有实数根
6．小区新增了一家快递店，第一天揽件200件，第三天揽件242件，设该快递店揽件日平均增长率为x，根据题意，下面所列方程正确的是（ ）
A．200（1+x）2＝242B．200（1﹣x）2＝242
C．200（1+2x）＝242D．200（1﹣2x）＝242
7．函数y＝ax2﹣a（a≠0）与y＝ax﹣a（a≠0）在同一平面直角坐标系中的图象可能是（ ）
A． B． C． D．
8．若a，b是方程x2+2x﹣2021＝0的两根，则a2+3a+b＝（ ）
A．2021B．2020C．2019D．2018
9．已知二次函数y＝2x2﹣4x﹣1在0≤x≤a时，y取得的最大值为15，则a的值为（ ）
A．1B．2C．3D．4
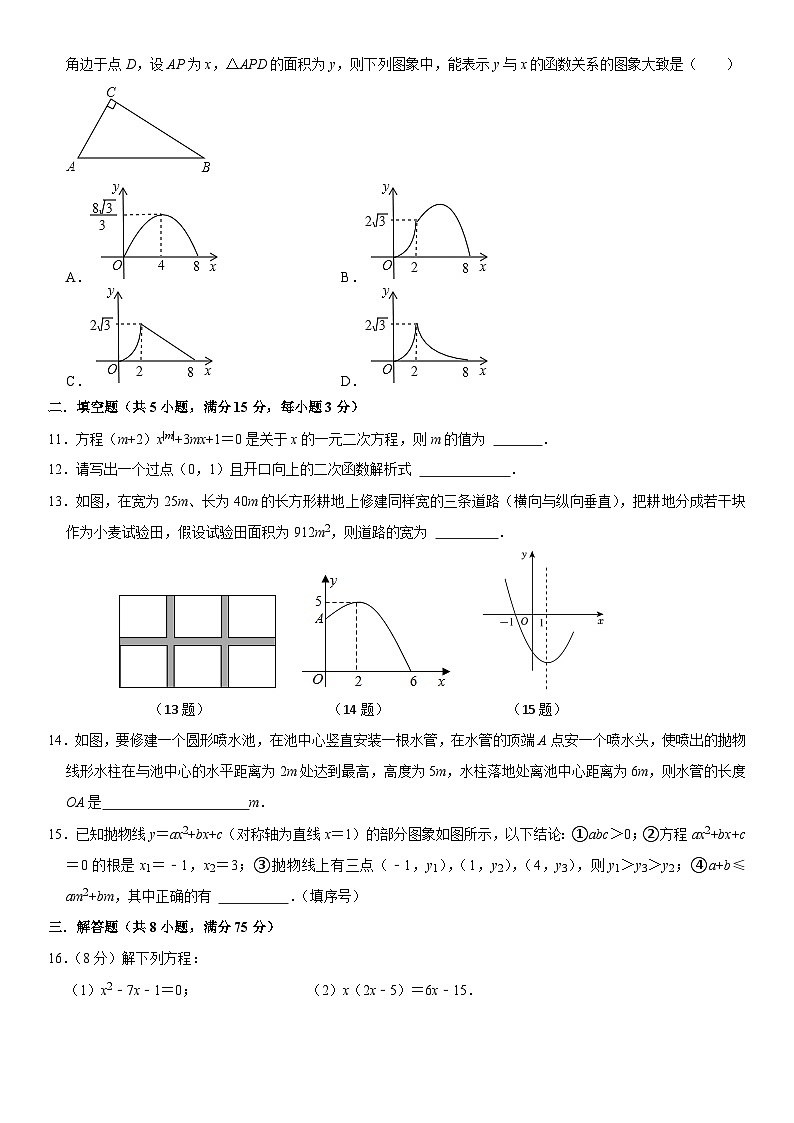
10．如图，在Rt△ACB中，∠C＝90°，∠A＝60°，AB＝8．点P是AB边上的一个动点，过点P作PD⊥AB交直角边于点D，设AP为x，△APD的面积为y，则下列图象中，能表示y与x的函数关系的图象大致是（ ）
A．B．
C．D．
二．填空题（共5小题，满分15分，每小题3分）
11．方程（m+2）x|m|+3mx+1＝0是关于x的一元二次方程，则m的值为 ．
12．请写出一个过点（0，1）且开口向上的二次函数解析式 ．
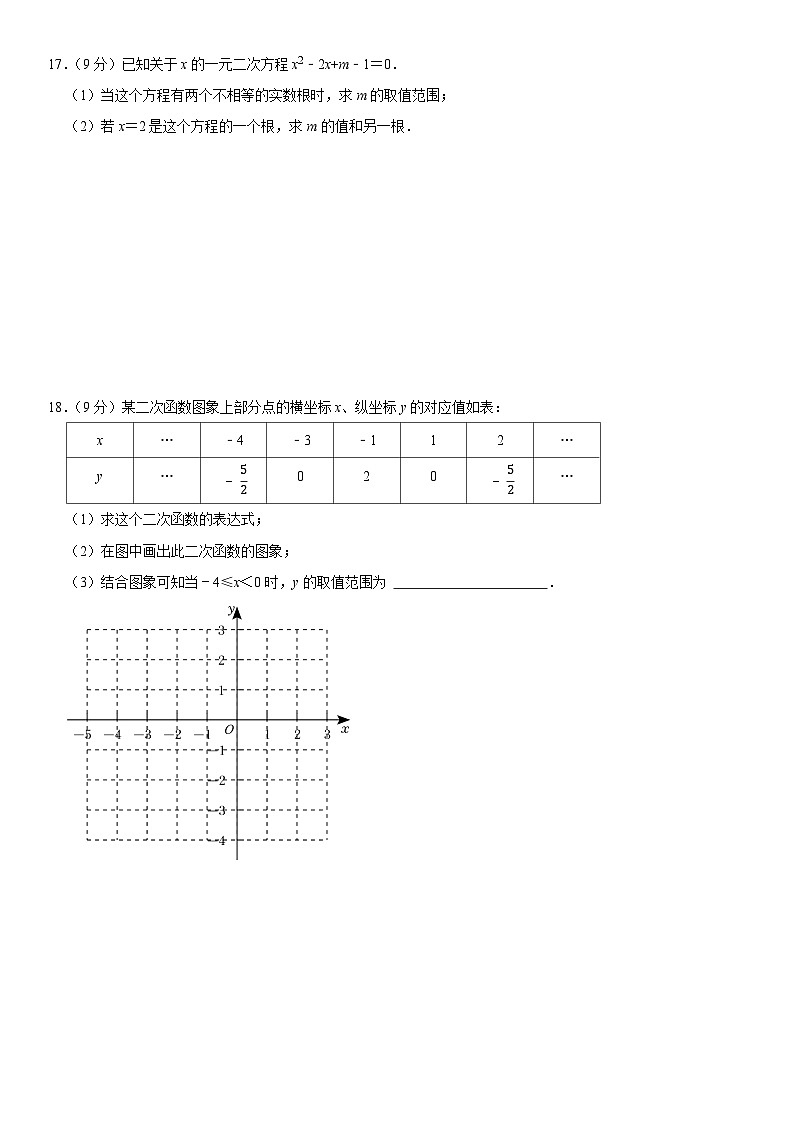
13．如图，在宽为25m、长为40m的长方形耕地上修建同样宽的三条道路（横向与纵向垂直），把耕地分成若干块作为小麦试验田，假设试验田面积为912m2，则道路的宽为 ．

（13题） （14题） （15题）
14．如图，要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端A点安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为2m处达到最高，高度为5m，水柱落地处离池中心距离为6m，则水管的长度OA是 m．
15．已知抛物线y＝ax2+bx+c（对称轴为直线x＝1）的部分图象如图所示，以下结论：①abc＞0；②方程ax2+bx+c＝0的根是x1＝﹣1，x2＝3；③抛物线上有三点（﹣1，y1），（1，y2），（4，y3），则y1＞y3＞y2；④a+b≤am2+bm，其中正确的有 ．（填序号）
三．解答题（共8小题，满分75分）
16．（8分）解下列方程：
（1）x2﹣7x﹣1＝0； （2）x（2x﹣5）＝6x﹣15．
17．（9分）已知关于x的一元二次方程x2﹣2x+m﹣1＝0．
（1）当这个方程有两个不相等的实数根时，求m的取值范围；
（2）若x＝2是这个方程的一个根，求m的值和另一根．
18．（9分）某二次函数图象上部分点的横坐标x、纵坐标y的对应值如表：
（1）求这个二次函数的表达式；
（2）在图中画出此二次函数的图象；
（3）结合图象可知当﹣4≤x＜0时，y的取值范围为 ．
19．（9分）公安交警部门提醒市民，骑车出行必须严格遵守“一盔一带”的规定．某头盔经销商统计了某品牌头盔4月份到6月份的销量，该品牌头盔4月份销售150个，6月份销售216个，且从4月份到6月份销售量的月增长率相同．
（1）求该品牌头盔销售量的月增长率；
（2）若此种头盔的进价为30元/个，测算在市场中，当售价为40元/个时，月销售量为600个，若在此基础上售价每上涨1元/个，则月销售量将减少10个，为使月销售利润达到10000元，而且尽可能让顾客得到实惠，则该品牌头盔的实际售价应定为多少元/个？
20．（9分）阅读材料：方程x2+2x﹣35＝0我们可以按下面的方法解答．
分解因式：x2+2x﹣35．
①竖分二次项与常数项：x2＝x•x，﹣35＝（﹣5）×（+7）．
②交叉相乘，验中项：⇒7x+（﹣5x）＝2x．
③横向写出两因式：x2+2x﹣35＝（x+7）（x﹣5）．
根据乘法原理：若ab＝0，则a＝0，或b＝0．所以方程x2+2x﹣35＝0可以这样求解：方程左边因式分解得（x+7）（x﹣5）＝0．所以原方程的解为x1＝﹣7，x2＝5．
试用上述方法和原理解下列方程：
（1）x2+5x+4＝0；
（2）x2﹣6x﹣7＝0；
（3）2x2+x﹣6＝0．
21．（10分）如图，在平面直角坐标系中，直线y=-32x+3与x轴，y轴分别交于点C，D，抛物线y=-14(x-2)2+k（k为常数）经过点D且交x轴于A，B两点．（1）求抛物线表示的函数解析式；
（2）若点P为抛物线的顶点，连接AD，DP，CP．求四边形ACPD的面积．
22．（10分）已知：a、b是关于x的方程x2﹣（m+3）x+2m+2＝0的两个实数根．
（1）求证：无论m取何值方程总有两个实数根；
（2）当a＝b时，m为何值？求出这时方程的解？
23．（11分）如图，二次函数y＝﹣x2+4x+5的图象与x轴交于A，B两点，与y轴交于点C，M为抛物线的顶点．
（1）求M点的坐标；
（2）求△MBC的面积；
（3）坐标轴上是否存在点N，使得以B，C，N为顶点的三角形是直角三角形？若存在，求出点N的坐标；若不存在，请说明理由．
参考答案
一．选择题（共10小题，满分30分，每小题3分）
1．解：一元二次方程3x2﹣8x﹣10＝0的一次项系数为﹣8；
选：B．
2．解：∵抛物线y＝3（x﹣2）2+1，
∴该抛物线的对称轴为直线x＝2，
选：D．
3．解：∵x2+4x+2＝0，
∴x2+4x＝﹣2，
∴x2+4x+4＝﹣2+4，即（x+2）2＝2，
选：A．
4．解：由题知，
y＝x2﹣2x﹣3＝（x﹣1）2﹣4，
由题中所给的平移可知，
y1=(x-1-1)2-4+2=（x﹣2）2﹣2＝x2﹣4x+2．
选：D．
5．解：∵Δ＝（﹣4）2﹣4×1×3＝4＞0，
∴方程有两个不相等的实数根．
选：B．
6．解：根据题意，可列方程：200（1+x）2＝242，
选：A．
7．解：①当a＞0时，二次函数y＝ax2﹣a的图象开口向上、对称轴为y轴、顶点在y轴负半轴，一次函数y＝ax﹣a（a≠0）的图象经过第一、三、四象限，且两个函数的图象交于y轴同一点；
②当a＜0时，二次函数y＝ax2﹣a的图象开口向下、对称轴为y轴、顶点在y轴正半轴，一次函数y＝ax﹣a（a≠0）的图象经过第一、二、四象限，且两个函数的图象交于y轴同一点．
对照四个选项可知C正确．
选：C．
8．解：∵a是方程x2+2x﹣2021＝0的根，
∴a2+2a﹣2021＝0，
即a2＝﹣2a+2021，
∴a2+3a+b＝﹣2a+2021+3a+b＝a+b+2021，
∵a，b是方程x2+2x﹣2021＝0的两根，
∴a+b＝﹣2，
∴a2+3a+b＝﹣2+2021＝2019．
选：C．
9．解：∵二次函数y＝2x2﹣4x﹣1＝2（x﹣1）2﹣3，
∴抛物线的对称轴为x＝1，顶点（1，﹣3），
∴当y＝﹣3时，x＝1，
当y＝15时，2（x﹣1）2﹣3＝15，
解得x＝4或x＝﹣2，
∵当0≤x≤a时，y的最大值为15，
∴a＝4，
选：D．
10．解：∵∠C＝90°，∠A＝60°，AB＝8，
∴AC＝4，BC＝43，
当点D在AC上时，y=12×AP×PD=12×x×3x=32x2；
当点D在BC上时，如图所示，
∵AP＝x，AB＝8，
∴BP＝8﹣x，又∠B＝30°，
∴PD=3(8-x)3，
∴y=12AP•PD=12x•3(8-x)3=-36x2+433x，
∴该函数图象前半部分是抛物线开口向上，后半部分也为抛物线开口向下．
选：B．
二．填空题（共5小题，满分15分，每小题3分）
11．解：∵方程（m+2）x|m|+3mx+1＝0是关于x的一元二次方程，
∴m+2≠0且|m|＝2，
解得：m＝2．
答案为：2．
12．解：∵开口向上，
∴a＞0，
且与y轴的交点为（0，1），
∴函数解析式可以为：y＝x2+1（答案不唯一），
答案为：y＝x2+1．
13．解：设道路的宽为x m，则种植小麦的部分可合成长为（40﹣2x）m，宽为（25﹣x）m的矩形，依题意得，
（40﹣2x）（25﹣x）＝912，
化简得x2﹣45x+44＝0．
解得：x1＝1，x2＝44（不合题意舍去）．
答案为：1m．
14．解：设抛物线的解析式为y＝a（x﹣h）2+k，
由题意可知抛物线的顶点坐标为（2，5），与x轴的一个交点为（6，0），
∴0＝a（6﹣2）2+5，
解得：a=-516，
∴抛物线的解析式为：y=-516（x﹣2）2+5，
当x＝0时，y=-516（0﹣2）2+5=154．
∴水管的长度OA是154m．
答案为：154．
15．解：∵抛物线y＝ax2+bx+c（对称轴为直线x＝1），
∴-b2a=1，
抛物线开口向上，
∴a＞0，
∴b＜0，
抛物线与y轴交于负半轴，
∴c＜0，
abc＞0，①正确；
抛物线与x轴交于（﹣1，0），对称轴为x＝1，
则抛物线与x轴另一个交点为交于（3，0），
②正确；
根据抛物线的增减性可知：当x＜1时，y随x增大而减小；当x＞1时，y随x增大而增大；
当x＝3和x＝﹣1时，y值相等；
y3＞y1＞y2，③错误；
已知对称轴为直线x＝1，
当x＝1时，y＝a+b+c是，取得最小值；
当x＝m时，y＝am2+bm+c，即a+b≤am2+bm，④正确；
答案为：①②④．
三．解答题（共8小题，满分75分）
16．解：（1）x2﹣7x﹣1＝0，
a＝1，b＝﹣7，c＝﹣1，
Δ＝b2﹣4ac＝49﹣4×1×（﹣1）＝53＞0，
∴x=7±532，
∴x1=7+532，x2=7-532；
（2）x（2x﹣5）＝6x﹣15．
x（2x﹣5）﹣3（2x﹣5）＝0，
（2x﹣5）（x﹣3）＝0，
∴2x﹣5＝0或x﹣3＝0，
∴x1=52．x2＝3．
17．解：（1）∵关于x的一元二次方程x2﹣2x+m﹣1＝0有两个不相等的实数根，
∴Δ＝b2﹣4ac＝（﹣2）2﹣4（m﹣1）＞0．
∴m＜2；
（2）∵x＝2是这个方程的一个根，
∴22﹣2×2+m﹣1＝0．
∴m＝1．
∴原方程为x2﹣2x＝0．
解得x1＝2，x2＝0，
即方程的另一根是x＝0．
18．解：（1）由题意，设二次函数的表达式为y＝a（x+3）（x﹣1），
∵二次函数经过点（﹣1，2），
∴﹣4a＝2，
∴a=-12，
∴二次函数的表达式为y=-12x2-x+32=-12(x+1)2+2；
（2）∵y=-12(x+1)2+2，
∴顶点为（﹣1，2），
描点、连线，画出图形如图所示：
（3）观察函数图象可知：当﹣4≤x＜0时，y的取值范围是-52≤y≤2，
答案为：-52≤y≤2．
19．解：（1）设该品牌头盔销售量的月增长率为x，
依题意，得：150（1+x）2＝216，
解得：x1＝0.2＝20%，x2＝﹣2.2（不合题意，舍去）．
答：该品牌头盔销售量的月增长率为20%．
（2）设该品牌头盔的实际售价为y元，
依题意，得：（y﹣30）[600﹣10（y﹣40）]＝10000，
整理，得：y2﹣130y+4000＝0，
解得：y1＝80（不合题意，舍去），y2＝50，
答：该品牌头盔的实际售价应定为50元．
20．解：（1）方程左边因式分解，得（x+1）•（x+4）＝0．
于是得x+1＝0或x+4＝0．
所以原方程的解为x1＝﹣1，x2＝﹣4；
（2）方程左边因式分解，得（x+1）（x﹣7）＝0．
于是得x+1＝0或x﹣7＝0．
所以原方程的解为x1＝﹣1，x2＝7；
（3）方程左边因式分解，得（2x﹣3）（x+2）＝0．
于是得2x﹣3＝0，或x+2＝0．
所以原方程的解为x1＝1.5，x2＝﹣2．
21．解：（1）在y=-32x+3中，令x＝0得y＝3，
∴D（0，3），
∵抛物线y=-14(x-2)2+k经过点D（0，3），
∴3=-14×（0﹣2）2+k，
解得k＝4，
∴y=-14（x﹣2）2+4=-14x2+x+3；
∴抛物线表示的函数解析式为y=-14x2+x+3；
（2）连接OP，如图；
在y=-32x+3中，令y＝0得x＝2，
∴C（2，0），OC＝2，
在y=-14x2+x+3中，令y＝0得0=-14x2+x+3，
解得x＝6或x＝﹣2，
∴A（﹣2，0），OA＝2，
由y=-14（x﹣2）2+4可得抛物线顶点P坐标为（2，4），
∴S四边形ACPD＝S△AOD+S△POD+S△POC=12×2×3+12×3×2+12×2×4＝3+3+3＝10；
∴四边形ACPD的面积为10．
22．（1）证明：∵关于x的方程x2﹣（m+3）x+2m+2＝0．
∴Δ＝[﹣（m+3）]2﹣4×1×（2m+2）＝m2﹣2m+1＝（m﹣1）2≥0，
∴无论m取何值，该方程都有实数根；
（2）解：∵a、b是关于x的方程x2﹣（m+3）x+2m+2＝0的两个实数根，且a＝b，
∴Δ＝（m﹣1）2＝0，
∴m＝1，
∴原方程为：x2﹣4x+4＝0，即（x﹣2）2＝0，
∴x1＝x2＝2．
23．解：（1）y＝﹣x2+4x+5＝﹣（x﹣2）2+9，
∴M（2，9）；
（2）令y＝0，得﹣x2+4x+5＝0，
解得 x＝﹣1或x＝5，
∴A（﹣1，0），B（5，0），
令x＝0，得y＝﹣x2+4x+5＝5，
∴C（0，5），
过点M作ME⊥y轴于点E，
∴S△MBC＝S四边形MBOE﹣S△MCE﹣S△BOC=12×(2+5)×9-12×2×(9-5)-12×5×5=15；
（3）存在点N，使得以B，C，N为顶点的三角形是直角三角形，理由如下：
∵OB＝OC＝5，∠COB＝90°，
∴∠OCB＝∠OBC＝45°，
∴△BOC是等腰直角三角形，
①当C为直角顶点时，作CN1⊥BC交坐标轴为N1，∠CN1B＝∠CBN1＝45°，
∴OB＝ON1＝5，
∴N1（﹣5，0）；
②当B为直角顶点时，作BN2⊥BC交坐标轴为N2，∠CN2B＝∠BCN2＝45°，
∴OC＝ON2＝5，
∴N1（0，﹣5）；
③当N为直角顶点时，点O与N3重合，
∴N3（0，0）．
综上所述，满足条件的点N的坐标为（﹣5，0）或（0，﹣5）或（0，0）．
题号
一
二
三
总分
得分
x
…
﹣4
﹣3
﹣1
1
2
…
y
…
-52
0
2
0
-52
…