07 第27讲　余弦定理、正弦定理 【正文】听课高考数学练习

这是一份07 第27讲　余弦定理、正弦定理 【正文】听课高考数学练习，共8页。试卷主要包含了掌握正弦定理、余弦定理及其变形，面积公式等内容，欢迎下载使用。

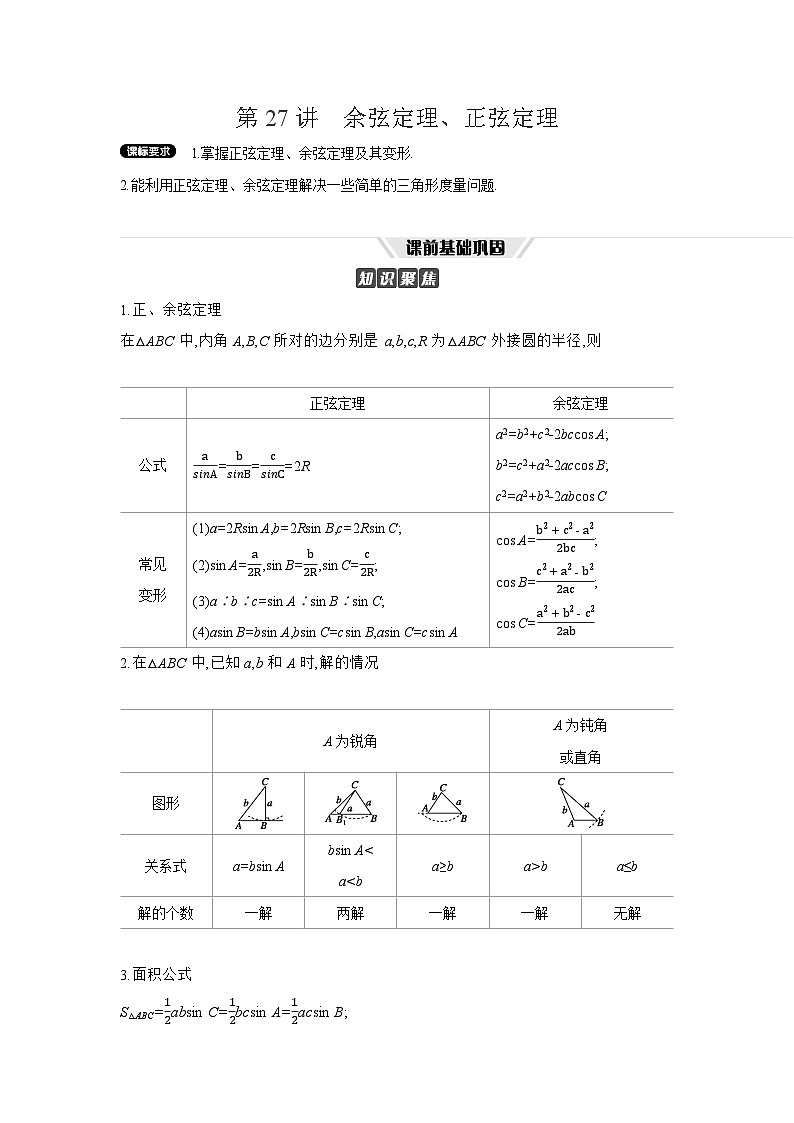
1.正、余弦定理
在△ABC中,内角A,B,C所对的边分别是a,b,c,R为△ABC外接圆的半径,则
2.在△ABC中,已知a,b和A时,解的情况
3.面积公式
S△ABC=12absin C=12bcsin A=12acsin B;
S△ABC=abc4R=12(a+b+c)·r(r是△ABC的内切圆半径,R是△ABC的外接圆半径,并可由此计算R,r).
S△ABC=p(p-a)(p-b)(p-c)p=12(a+b+c)
常用结论
1.正弦定理的应用
①边化角,角化边⇔a∶b∶c=sin A∶sin B∶sin C.
②大边对大角,大角对大边
a>b⇔A>B⇔sin A>sin B⇔cs Asin B,则A,B的大小关系为 .
6.在△ABC中,内角A,B,C的对边分别为a,b,c,已知B=30°,b=2,c=2,则C= .
7.在△ABC中,内角A,B,C所对的边分别为a,b,c,若a=2,c=3,B=30°,则S△ABC= ,b= .
利用余弦定理、正弦定理解基本
量问题
例1 [2024·北京丰台区期中] 在△ABC中,内角A,B,C所对的边分别为a,b,c,且a=5,b=11,cs C=35.
(1)求△ABC的面积;
(2)求c及sin A的值.


总结反思
(1)正弦定理、余弦定理的作用是在已知三角形部分元素的情况下求解其余元素,基本思想是方程思想,即根据正弦定理、余弦定理列出关于未知元素的方程(组),通过解方程(组)求得未知元素.
(2)正弦定理、余弦定理的另一个作用是实现三角形边角关系的互化,解题时可以把已知条件化为角的三角函数关系,也可以把已知条件化为三角形边的关系.
变式题1 (1)[2023·全国乙卷] 在△ABC中,内角A,B,C的对边分别是a,b,c,若acs B-bcs A=c,且C=π5,则B=( )
A.π10B.π5C.3π10D.2π5
(2)[2023·北京卷] 在△ABC中,(a+c)(sin A-sin C)=b(sin A-sin B),则∠C=( )
A.π6B.π3C.2π3D.5π6
(3)记△ABC的内角A,B,C的对边分别为a,b,c,面积为3,B=60°,a2+c2=3ac,则b= .
变式题2 [2023·天津卷] 在△ABC中,角A,B,C所对的边分别是a,b,c.已知a=39,b=2,∠A=120°.
(1)求sin B的值;
(2)求c的值;
(3)求sin(B-C).


利用余弦定理、正弦定理判定三角形的形状
例2 (1)在△ABC中,若csAcsB=ba=43,则△ABC是( )
A.等腰三角形
B.直角三角形
C.等腰或直角三角形
D.钝角三角形
(2)在△ABC中,已知a2+b2-c2=ab,且2cs Asin B=sin C,则该三角形的形状是( )
A.直角三角形
B.等腰三角形
C.等边三角形
D.钝角三角形
总结反思
判断三角形形状的两种思路
(1)化边:通过因式分解、配方等得出边的相应关系,从而判断三角形的形状.
(2)化角:通过三角恒等变换,得出内角的关系,从而判断三角形的形状.此时要注意应用A+B+C=π这个结论.
变式题 (1)(多选题)已知△ABC的内角A,B,C所对的边分别为a,b,c,则下列说法中正确的有( )
A.若acsA=bcsB=ccsC,则△ABC一定是等边三角形
B.若acs A=bcs B,则△ABC一定是等腰三角形
C.若bcs C+ccs B=b,则△ABC一定是等腰三角形
D.若a2+b2