青岛版七年级数学上册期末素养综合测试(一)课件

这是一份青岛版七年级数学上册期末素养综合测试(一)课件，共57页。

一、选择题(每小题3分,共36分)1.(2023湖南衡阳中考)中国是最早采用正负数表示具有相反 意义的量并进行负数运算的国家,若收入500元记作+500元, 则支出237元记作(　    )A.+237元　　　    B.-237元　　　    C.0元　　　    D.-474元
解析　收入500元记作+500元,则支出237元应记作-237元,故 选B.
2.(新独家原创)2024年1月18日,国家统计局发布了2023年我 国GDP总量,已经达到了1 260 582亿元,按不变价格计算,比 上年增长了5.2%.其中1 260 582亿用科学记数法可表示为 (　    ) 582×1014　　　     82× 582×1015　　　     82×1015
解析    1 260 582亿=126 058 200 000 000=1.260 582×1014,故 选A.
3.(2024河北衡水景县期末)下列说法正确的是 (　    )A.- 的系数是-2B.32ab3的次数是6C. 是多项式D.x2+x-1的常数项为1
解析    A.- 的系数是- ;B.32ab3的次数是1+3=4;C.根据多项式的定义知, 是多项式;D.x2+x-1的常数项为-1.故选C.
4.下列说法中,正确的是 (　    )A.若|a|=|b|,则a=bB.若0b2,则a>bD.若a>b,则|a|>|b|
解析　当|a|=|b|时,a=b或a=-b,选项A错误;当022,但-3<2,选项C错误;2>-3,但|2|<|-3|,选项D错 误.故选B.
5.(新考向·新定义试题)(2023广东珠海期中)定义运算:m⊗n= m2-n3.例如3⊗2=32-23=1,则(-1)⊗(-2)= (　    )A.-7　　　    B.-5　　　    C.3　　　    D.9
解析　由题意,得(-1)⊗(-2)=(-1)2-(-2)3=1+8=9.故选D.
6.(2024山东聊城东阿期末)若方程(k-1)  =3是关于x的一元一次方程,则k等于(　    )A.1　　　    B.2　　　    C.-1　　　    D.3
解析　∵(k-1)x|k-2|=3是关于x的一元一次方程,∴k-1≠0且|k-2|=1,解得k=3.故选D.
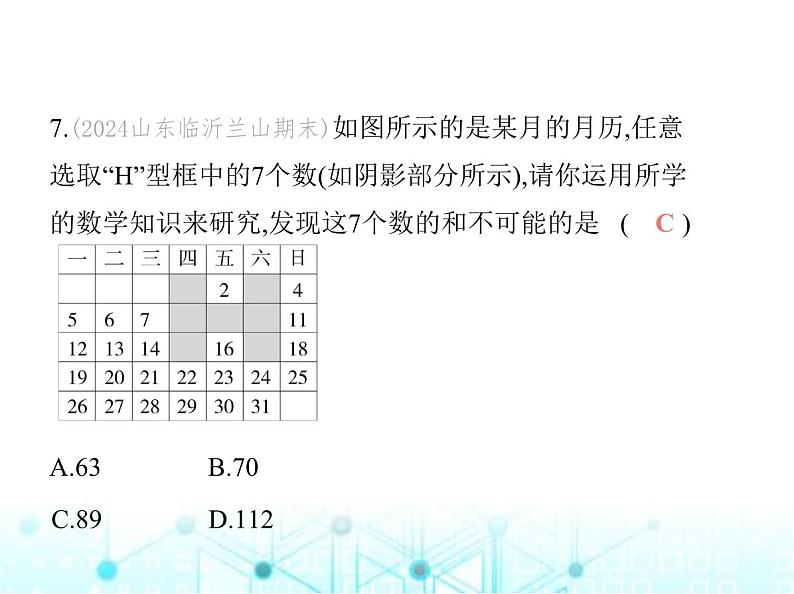
7.(2024山东临沂兰山期末)如图所示的是某月的月历,任意 选取“H”型框中的7个数(如阴影部分所示),请你运用所学 的数学知识来研究,发现这7个数的和不可能的是 (　    )A.63　　　    B.70　　　    
C.89　　　    D.112
解析　设“H”型框中7个数的中间数为x,则另外6个数分别 为(x-8),(x-6),(x-1),(x+1),(x+6),(x+8),故这7个数的和为(x-8)+(x -6)+(x-1)+x+(x+1)+(x+6)+(x+8)=,解得x=9,∴这7个 数的和可能是63,故选项A不符合题意;B.7x=70,解得x=10,∴这7个数的和可能是70,故选项B不符合题意;C.7x=89,解得x=  ,∴这7个数的和不可能是89,故选项C符合题意;D.7x=112,解得x=16,∴这7个数的和可能是112,故选项D不符合题意.故 选C.
8.(2023山东济宁任城期末)在利用太阳能热水器来加热水的 过程中,热水器里的水温会随着太阳照射时间的变化而变化, 在这个变化过程中,自变量是 (　    )A.热水器里的水温　　　    B.太阳光的强弱C.热水器的容积　　　    D.太阳照射时间的长短
解析　热水器里的水温会随着太阳照射时间的变化而变化, 故自变量是太阳照射时间的长短.故选D.
9.(情境题·数学文化)(2024山东泰安肥城期末)《九章算术》 是我国古代数学名著,卷七“盈不足”中有题译文如下:现有 一伙人共同买一个物品,每人出8钱,还余3钱;每人出7钱,还差 4钱,问人数、物价各是多少?设物价为x钱,根据题意可列出 方程 (　    )A.8x+3=7x-4　　　    B. = C.8x-3=7x+4　　　    D. = 
解析　根据人数是不变的和每人出8钱,还余3钱,每人出7钱, 还差4钱,可以列出方程 = ,故选B.
10.(跨学科·化学)(2023山东滨州中考)由化学知识可知,用pH 表示溶液酸碱性的强弱程度,当pH>7时溶液呈碱性,当pH<7 时溶液呈酸性,若将给定的NaOH溶液加水稀释,那么在下列 图象中,能大致反映NaOH溶液的pH与所加水的体积V之间 对应关系的是 (　    )A. 　　　    B. 
C. 　　　    D. 
解析　将给定的NaOH溶液加水稀释,那么开始时pH>7,随着 慢慢加水,溶液碱性越来越弱,pH逐渐减小,但始终大于7.故 选B.
11.(2024山东菏泽单县期中)如图,AD=9,BD=2,若点E在直线 AD上,AE=1,则BE的长为 (　    ) A.6　　　    B.8　　　    C.6或8　　　    D.8或10
解析　分两种情况:当点E在线段AD上时,如图, ∵AD=9,BD=2,∴AB=AD-BD=9-2=7,∵AE=1,∴BE=AB-AE=7-1=6;当点E在线段DA的延长线上时,如图, 
∵AD=9,BD=2,∴AB=AD-BD=9-2=7,∵AE=1,∴BE=AB+AE=7+1=8.综上所述,BE的长为6或8,故选C.
12.(2024重庆忠县期末)如图所示,∠AOB=3∠COD=60°.将∠COD绕点O旋转,当∠COB=3∠AOD时,∠AOD= (　    ) A.20°　　　    B.40°C.60°　　　    D.20°或40°
解析　∵∠AOB=3∠COD=60°,∴∠COD=20°.分两种情况:①如图1,当OD在∠AOB内部时, 图1设∠AOD=x,则∠AOC=x-20°,∠BOD=60°-x,∴∠BOC=∠AOB-∠AOC=80°-x,∵∠COB=3∠AOD,
∴80°-x=3x,解得x=20°,此时OD在∠AOB内部,符合题意.②如图2,当OD在∠AOB外部时, 图2设∠AOD=x,则∠BOC=80°+x,∵∠COB=3∠AOD,∴80°+x=3x,
解得x=40°.综上,∠AOD=20°或40°.故选D.
二、填空题(每小题3分,共18分)13.(2024山东菏泽曹县期末)已知a2-a-1=0,则代数式3a2-a减2 a-4的差为　　　　　　    .
解析　∵a2-a-1=0,∴a2-a=1,∴3a2-a-(2a-4)=3a2-a-2a+4=3a2-3a+4=3(a2-a)+4=3×1+4=7.
14.若2解析　∵20,5-x>0,∴|x-2|-|5-x|=x-2-(5-x)=x-2-5+x=2x-7.
15.已知A,B,C为同一条直线上的三点,AB=9 cm,BC=1 cm,那 么A,C两点间的距离是　 　 　    .
 8 cm或10 cm
解析　分两种情况:①当点C在线段AB上时,如图,AC=AB-BC=9-1=8(cm). ②当点C在线段AB的延长线上时,如图,AC=AB+BC=9+1=10 (cm). 综上,AC=8 cm或10 cm.
16.若单项式 ax2yn+1与- axmy4的差仍是单项式,则m-2n=　     　    .
解析　∵单项式 ax2yn+1与- axmy4的差仍是单项式,∴单项式 ax2yn+1与- axmy4是同类项,∴m=2,n+1=4,∴n=3,∴m-2n=2-2×3=-4.
17.(2024山东青岛城阳期末)如图所示的是一个“数值转换 机”,若开始输入x的值是5,则第1次输出的结果是8,第2次输 出的结果是4,第3次输出的结果是2,第2 025次输出的结果是 　　　    . 
解析　若开始输入x的值是5,则第1次输出的结果是8,第2次输出的结果是4,第3次输出的结果是2,第4次输出的结果是1,第5次输出的结果是4,第6次输出的结果是2,第7次输出的结果是1,……∴从第2次开始,输出的结果以4,2,1为一个循环组依次出现,
∵(2 025-1)÷3=674……2,∴第2 025次输出的结果与第3次输出的结果相同,∴第2 025次输出的结果是2.故答案为2.
18.(2024山东济宁微山期末)我国元代数学家朱世杰所撰写 的《算学启蒙》中有这样一道题:“良马日行二百四十里,驽 马日行一百五十里,驽马先行一十二日,问良马几何追及 之.”译文:良马平均每天能跑240里,驽马平均每天能跑150 里.现驽马出发12天后,良马从同一地点出发沿同一路线追 它,问良马多少天能够追上驽马?设良马x天能够追上驽马,根 据题意可列一元一次方程　　　　　　　　　    .
150(x+12)=240x
解析　根据路程=速度×时间结合总路程相等,即可得出关于 x的一元一次方程150(x+12)=240x.
三、解答题(共66分)19.[答案含评分细则](2024山东济南章丘期末)(6分)计算:(1) ×(-24).(2)-14+16÷(-2)3×|-3-1|.
解析    (1) ×(-24)=- ×(-24)+ ×(-24)- ×(-24) (1分)=16-15+4 (2分)=5. (3分)(2)-14+16÷(-2)3×|-3-1|=-1+16÷(-8)×4 (4分)=-1-8 (5分)=-9. (6分)
20.[答案含评分细则](2024山东日照东港期末)(8分)解方程:(1)2(x-2)=8-3(4x-1).(2) -1= - .
解析    (1)2(x-2)=8-3(4x-1),去括号,得2x-4=8-12x+3, (1分)移项,得2x+12x=8+3+4, (2分)合并同类项,得14x=15, (3分)系数化为1,得x= . (4分)(2) -1= - ,去分母,得10(3y+2)-20=5(2y-1)-4(2y+1), (5分)去括号,得30y+20-20=10y-5-8y-4, (6分)
移项,得30y-10y+8y=-5-4-20+20,合并同类项,得28y=-9, (7分)系数化为1,得y=- . (8分)
21.[答案含评分细则](2024河北石家庄桥西期中)(8分)如图, 平面上有三个点A,B,C.(1)根据下列语句画图:作出射线AC,CB,直线AB;在射线CB上 取一点D(不与点C重合),使BD=BC.(2)在(1)的条件下,回答问题:①用适当的语句表述点D与直线AB的位置关系:　　　　     　　    .②若BD=1.5,则CD=　　　    .
解析    (1)如图所示.  (4分)(2)①点D在直线AB外(或直线AB不经过点D). (6分)②∵BC=BD,BD=1.5,∴CD=2BD=3.故答案为3. (8分)
22.[答案含评分细则](2024山东济南平阴期末)(8分)某玩具 店购进吉祥物“琮琮”“莲莲”共100个,总费用为6 600元, 这两种吉祥物的进价如表:
问:该玩具店购进“琮琮”和“莲莲”各多少个?
解析　设该玩具店购进“琮琮”x个,则购进“莲莲”(100-x) 个, (1分)根据题意得60x+70(100-x)=6 600, (4分)解得x=40. (6分)100-40=60.答:该玩具店购进“琮琮”40个,“莲莲”60个. (8分)
23.[答案含评分细则](2024山东临沂临沭期末)(8分)(1)先化简,再求值:2(x2-3x)-(2x-1)+3x2,其中x=-2.(2)已知x+3=0,A=3x2-5xy+3y-1,B=x2-2xy,求A-3B的值.
解析    (1)2(x2-3x)-(2x-1)+3x2=2x2-6x-2x+1+3x2 (1分)=5x2-8x+1, (2分)当x=-2时,原式=5×(-2)2-8×(-2)+1 (3分)=20+16+1=37. (4分)(2)A-3B=3x2-5xy+3y-1-3(x2-2xy)=3x2-5xy+3y-1-3x2+6xy
=xy+3y-1, (6分)当x+3=0时,x=-3, (7分)原式=-3y+3y-1=-1. (8分)
24.[答案含评分细则](2024山东济宁曲阜期末)(8分)如图1,直 角三角板COD的直角顶点O在直线AB上,线段OC,OD是三角 板的两条直角边,射线OE是∠AOD的平分线.(1)当∠COE=35°时,∠BOD=　　　    °.(2)当∠COE=β时,∠BOD=　　　    (用含β的式子表示).(3)当三角板绕点O逆时针旋转到如图2所示的位置时,若∠ COE=β,其他条件不变,则∠BOD=　　　    (用含β的式子表 示).
解析    (1)∵∠COD=90°,∠COE=35°,∴∠DOE=90°-35°=55°.∵OE平分∠AOD,∴∠AOD=2∠DOE=2×55°=110°,∴∠BOD=180°-∠AOD=180°-110°=70°.故答案为70. (2分)(2)∵∠COD=90°,∠COE=β,∴∠DOE=90°-β.∵OE平分∠AOD,
∴∠AOD=2∠DOE=2×(90°-β)=180°-2β,∴∠BOD=180°-∠AOD=180°-(180°-2β)=2β.故答案为2β. (5分)(3)∵OE平分∠AOD,∠DOE=β-90°,∴∠AOD=2∠DOE=2β-180°,∴∠BOD=180°-∠AOD=180°-(2β-180°)=180°-2β+180°=360°-2β.故答案为(360°-2β). (8分)
25.[答案含评分细则](2023山东滨州阳信期中)(10分)阅读材 料:如图,在数轴上A点所表示的数为a,B点所表示的数为b,点 A到点B的距离记为AB,线段AB的长可以用右边的数减去左 边的数来表示,即AB=b-a. 请用上面的知识解决下面的问题:已知数轴上点A、C表示的数分别为a,c,且满足|a+7|+|c-2|=0, 点B表示的数为-3.
(1)a=　　　    ,c=　　　    .(2)若在数轴上有两动点P、Q分别从点A、B同时出发向右 运动,点P的速度为2个单位长度/秒,点Q的速度为1个单位长 度/秒,求经过多长时间P、Q两点间的距离为3.(3)在数轴上找一点M,使得点M到点A和点C的距离之和为15, 请求出点M所表示的数.
解析    (1)-7;2. (2分)(2)点A表示的数为-7,点B表示的数为-3,设运动时间为t秒,则点P表示的数是-7+2t,点Q表示的数是-3 +t,①当点P在点Q左侧时,-3+t-(-7+2t)=3,解得t=1. (4分)②当点P在点Q右侧时,-7+2t-(-3+t)=3,
解得t=7.∴经过1秒或7秒时,P、Q两点间的距离为3. (6分)(3)由(1)可知,点A表示的数是-7,点C表示的数是2,设点M表示的数是m,分两种情况:①当点M在点A的左侧时,MA=-7-m,MC=2-m,则-7-m+2-m=15,解得m=-10. (8分)②当点M在点C的右侧时,
MA=m-(-7),MC=m-2,则m-(-7)+m-2=15,解得m=5.综上,点M表示的数是-10或5. (10分)
26.[答案含评分细则](2024山东德州乐陵期末)(10分)七、八 年级共有92名学生参与元旦表演(其中七年级人数多于八年 级,且七年级人数不到90名,八年级人数不到46名),下面是某 服装店给出的演出服装的价格表:
如果两个年级自己单独购买服装,一共应付5 000元.(1)若七、八年级联合购买服装,则比各自购买服装共可以节 省多少元?(2)七、八年级各有多少名学生参加表演(列方程求解)?(3)如果七年级有10名同学因故不能参加表演,请你为这两个 年级设计一种最省钱的购买服装的方案.
解析    (1)5 000-92×40=1 320(元).答:七、八年级联合起来购买服装比各自购买服装共可以节 省1 320元. (2分)(2)设七年级有x名学生参加表演,则八年级有(92-x)名学生参 加表演.由题意得50x+60(92-x)=5 000, (4分)解得x=52, (6分)则92-x=40.答:七年级有52名学生参加表演,八年级有40名学生参加表
演. (6分)(3)∵七年级有10人不能参加表演,∴七年级有52-10=42人参加表演. (7分)若七、八年级联合购买服装,则需要50×(42+40)=4 100(元),  (8分)此时比各自购买服装节省(42+40)×60-4 100=820(元),但如果七、八年级联合购买91套服装,只需40×91=3 640(元),此时又比联合购买服装节省4 100-3 640=460(元), (9分)