北京市顺义区第一中学2023-2024学年高二上学期10月考试数学试卷（Word版附解析）

这是一份北京市顺义区第一中学2023-2024学年高二上学期10月考试数学试卷（Word版附解析），文件包含北京市顺义区第一中学2023-2024学年高二上学期10月考试数学试题Word版含解析docx、北京市顺义区第一中学2023-2024学年高二上学期10月考试数学试题Word版无答案docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。

本试卷共4页，150分.考试时长120分钟.考生务必将答案答在答题卡上，在试卷上作答无效.考试结束后，将答题卡交回.
一. 单选题（本大题共10 小题，共40.0分）
1. 已知向量，，则（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据空间向量线性运算的坐标表示求解.
【详解】∵，
∴
故选：A.
2. 空间四边形中，，，，则等于（ ）
A. B. C. D.
【答案】B
【解析】
【分析】根据向量的三角形法则，即可求解.
【详解】如图所示，根据向量的运算，可得.
故选：B.
3. 已知空间向量，则“”是“”的（ ）
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
【答案】A
【解析】
【分析】利用充分条件和必要条件的定义判断.
【详解】当时，，所以，即，故充分；
当时，，即解得，故不必要；
故选：A
【点睛】本题主要考查逻辑条件的判断以及空间向量的数量积运算，属于基础题.
4. 已知向量，且，那么（ ）
A. B. C. D.
【答案】A
【解析】
【分析】根据题意，设，即，，，2，，分析可得、的值，进而由向量模的计算公式计算可得答案．
【详解】根据题意，向量，2，，，，，且，
则设，即，，，2，，
则有，则，，
则，，，故；
故选：A．
5. 已知是空间的一个基底，在下列向量中，与向量，一定可以构成空间的另一个基底的是（ ）
A. B. C. D.
【答案】C
【解析】
【分析】根据空间向量基底的定义依次判断各选项即可.
【详解】解：对于A选项，，故不能构成空间的另一个基底；
对于B选项，，故不能构成空间的另一个基底；
对于C选项，不存在使得成立，故能构成空间的另一个基底；
对于D选项，假设存在使得，则，解得，故，故不能构成空间的另一个基底；
故选：C
6. 在空间直角坐标系中，点关于平面的对称点为，则
A. B. C. D.
【答案】D
【解析】
【分析】由题意，根据点关于平面的对称点，求得的坐标，利用向量的数量积的坐标运算，即求解.
【详解】由题意，空间直角坐标系中，点关于平面的对称点，
所以,则，故选D.
【点睛】本题主要考查了空间直角坐标系的应用，以及空间向量的数量积的坐标运算，其中解答中熟记空间向量数量积的坐标运算公式，准确运算是解答的关键，着重考查了推理与运算能力，属于基础题.
7. 已知两点，，过点的直线l与线段AB有公共点，则直线l的斜率k的取值范围是
A. B.
C. D.
【答案】D
【解析】
【详解】分析：根据两点间的斜率公式，利用数形结合即可求出直线斜率的取值范围．
详解：∵点A（﹣3，4），B（3，2），过点P（1，0）的直线L与线段AB有公共点，
∴直线l的斜率k≥kPB或k≤kPA，
∵PA的斜率为 =﹣1，PB的斜率为=1，
∴直线l的斜率k≥1或k≤﹣1，
故选D．
点睛：本题主要考查直线的斜率的求法，利用数形结合是解决本题的关键，比较基础．直线的倾斜角和斜率的变化是紧密相联的，tana=k,一般在分析角的变化引起斜率变化的过程时，是要画出正切的函数图像，再分析.
8. 正方体不在同一表面上的两顶点，，则正方体的体积是（ ）
A. 4B. C. 64D.
【答案】C
【解析】
【分析】先根据题意可知AB是正方体的体对角线，利用空间两点的距离公式求出AB，再根据正方体的棱长求出体积．
【详解】解：∵正方体中不在同一表面上两顶点，，
∴AB是正方体的体对角线，，
∴正方体的棱长为4，正方体的体积为64．
故选：C．
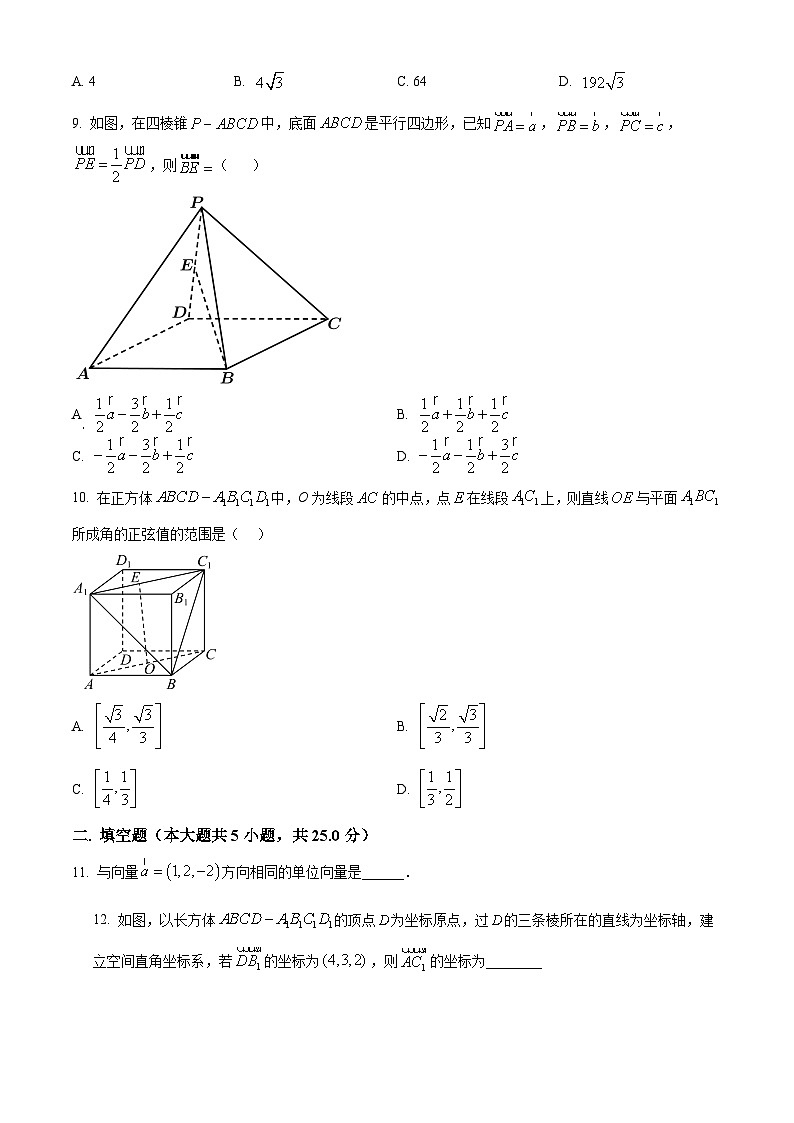
9. 如图，在四棱锥中，底面是平行四边形，已知，，，，则（ ）
A B.
C. D.
【答案】A
【解析】
【分析】利用空间向量的线性运算即可求解.
【详解】因为在四棱锥中，底面是正方形，，，，，
所以
．
故选：A．
10. 在正方体中，O为线段的中点，点在线段上，则直线与平面所成角的正弦值的范围是（ ）

A. B.
C. D.
【答案】B
【解析】
【分析】设正方体边长为2，如图，以D为原点建立空间直角坐标系，后由空间向量知识可得与平面所成角的正弦值的表达式，即可得答案.
【详解】设正方体边长为2，如图，以D为原点建立空间直角坐标系.
则.
因点在线段上，设， .
则，
， .
设平面法向量为，
则，取.
设与平面所成角为，
则.
注意到，则
.
故选：B

二. 填空题（本大题共5小题，共25.0分）
11. 与向量方向相同的单位向量是______．
【答案】
【解析】
【分析】由与方向相同的单位向量是可计算求得结果.
【详解】，，
即与向量方向相同单位向量是.
故答案为：.
12. 如图，以长方体的顶点为坐标原点，过的三条棱所在的直线为坐标轴，建立空间直角坐标系，若的坐标为，则的坐标为________
【答案】
【解析】
【详解】 如图所示，以长方体的顶点为坐标原点，
过的三条棱所在直线为坐标轴，建立空间直角坐标系，
因为的坐标为，所以,
所以.
13. 若过点P(1－a,1＋a)与点Q(3,2a)的直线的倾斜角是钝角，则实数a的取值范围是________．
【答案】(－2,1)
【解析】
【详解】试题分析：由直线的倾斜角α为钝角，能得出直线的斜率小于0，解不等式求出实数a的取值范围．解：∵过点P（1-a，1+a）和Q（3，2a）的直线的倾斜角α为钝角，∴直线的斜率小于0， ，故答案为
考点：直线的斜率公式
点评：本题考查直线的斜率公式及直线的倾斜角与斜率的关系．
14. 已知正方体的棱长为1，则点B到直线的距离为_________．
【答案】
【解析】
【分析】连接，过B作，则即为所求，由三角形等面积计算求解.
【详解】解：如图，连接，过B作，则即为点B到直线的距离，
在正方体中，平面，，在直角中，，且，所以 ，点B到直线的距离为.
故答案为：.
15. 在棱长为1的正方体中，点M和N分别是正方形ABCD和的中心，点P为正方体表面上及内部的点，若点P满足，其中m、n、，且，则满足条件的所有点P构成的图形的面积是______．
【答案】
【解析】
【分析】因为点P满足，其中m、n、，且，所以点A，M，N三点共面，只需要找到平面AMN与正方体表面的交线即可．
【详解】
因为点P满足，其中m、n、，且，
所以点A，M，N三点共面，
又因为M和N分别是矩形ABCD和的中心，所以，，
连接MN，，则，所以即为经过A，M，N三点的平面与正方体的截面，
故P点可以是正方体表面上线段，，AC上的点．
所以所有点P构成的图形的面积为．
故答案为：．
三、解答题（本大题共6小题，共85.0分.解答应写出文字说明，证明过程或演算步骤）
16. 已知直线l1过点A(1，1)，B(3，a)，直线l2过点M(2，2)，N(3+a，4).
（1）若l1l2，求a的值；
（2）若l1⊥l2，求a的值.
【答案】（1）；（2）.
【解析】
【分析】（1）由直线平行知斜率相等，建立等量关系得解.
（2）由直线垂直知斜率积为-1，建立等量关系得解.
【详解】解：设直线l1的斜率为k1，直线l2的斜率为k2.
（1）因为，所以存在且.
因为，所以，即，解得.
当时，，所以A，B，M不共线，则符合题意.
（2），
①当时，，不符合题意；
②当时，，因为，所以存在且，
则，即，解得.
17. 如图，在平行六面体.，设向量

（1）用表示向量
（2）求
【答案】（1），
（2）
【解析】
【分析】（1）利用空间向量基本定理与空间向量的线性运算可得出关于的表达式；（2）由（1）知，利用空间向量数量积的运算可求得.
【小问1详解】
，
；
【小问2详解】
由（1）知，
由已知可得，
所以.
18. 已知四棱锥中，底面ABCD是正方形，平面ABCD，，E是PB的中点.

（1）求直线BD与直线PC所成角的余弦值；
（2）求证：平面
（3）求点到平面的距离.
【答案】（1）
（2）证明见解析 （3）
【解析】
【分析】（1）建立如图所示空间直角坐标系，利用空间向量法计算异面直线所成角的余弦值；
（2）利用数量积坐标运算得线线垂直，利用线线垂直证明线面垂直；
（3）利用点到平面距离向量公式直接计算即可.
【小问1详解】
以点为原点，分别以，，所在直线为，，轴，建立如图空间直角坐标系.

由题意，，，，，，
设直线BD与直线PC所成的角为，
因为，，所以，
所以直线BD与直线PC所成角的余弦值为；
【小问2详解】
因为，，，
所以，，
所以，又平面，
所以平面；
【小问3详解】
由（2）知，为平面的一个法向量，
设点到平面的距离为，则为向量在向量上的投影的绝对值，
由，得，
所以点到平面的距离为.
19. 在三棱柱中，侧面 为矩形，平面， D，E分别是棱 的中点.

（1）求证： 平面；
（2）若，求直线与平面 所成角的正弦值.
【答案】（1）答案见详解
（2）
【解析】
【分析】（1）由棱柱的性质证得四边形是平行四边形，从而利用线面平行的判定定理可证；
（2）建立空间直角坐标系，利用向量法求直线与平面 所成角的正弦值.
【小问1详解】
在三棱柱中，，且，
因为D，E分别是棱 的中点，
所以，且,
所以四边形是平行四边形，所以,
又平面，平面，
所以平面.
【小问2详解】
分别以所在直线为轴，轴，轴建立如图所示
的空间直角坐标系，
由题意得，，
所以，，，
设平面的法向量为，
则，即，
令，则，，于是，
所以，
所以直线与平面 所成角的正弦值.

20. 如图1，在Rt△ABC中，∠C＝90°，BC＝3，AC＝6，D，E分别是AC，AB上的点，且DE∥BC，DE＝2．将△ADE沿DE折起到△A1DE的位置，使A1C⊥CD，如图2．
(1)求证：A1C⊥平面BCDE；
(2)若M是A1D的中点，求CM与平面A1BE所成角的大小；
(3)线段BC上否存在点P，使平面A1DP与平面A1BE垂直？说明理由．
【答案】（1）略 （2） (3)见解析
【考点定位】此题第二问是对基本功的考查，对于知识掌握不牢靠的学生可能不能顺利解答．
第三问的创新式问法，难度非常大
【解析】
【详解】试题分析：（1）证明A1C⊥平面BCDE，因为A1C⊥CD，只需证明A1C⊥DE，即证明DE⊥平面A1CD；
（2）建立空间直角坐标系，用坐标表示点与向量，求出平面A1BE法向量，=（﹣1，0，），利用向量的夹角公式，即可求得CM与平面A1BE所成角的大小；
（3）设线段BC上存在点P，设P点坐标（0，a，0），则a∈[0，3]，求出平面A1DP法向量为
假设平面A1DP与平面A1BE垂直，则，可求得0≤a≤3，从而可得结论．
（1）证明：∵CD⊥DE，A1D⊥DE，CD∩A1D=D，
∴DE⊥平面A1CD，
又∵A1C⊂平面A1CD，∴A1C⊥DE
又A1C⊥CD，CD∩DE=D
∴A1C⊥平面BCDE
（2）解：如图建系，则C（0，0，0），D（﹣2，0，0），A1（0，0，2），B（0，3，0），E（﹣2，2，0）
∴，
设平面A1BE法向量为
则∴∴
∴
又∵M（﹣1，0，），∴=（﹣1，0，）
∴
∴CM与平面A1BE所成角的大小45°
（3）解：设线段BC上存在点P，设P点坐标为（0，a，0），则a∈[0，3]
∴，
设平面A1DP法向量为
则∴
∴
假设平面A1DP与平面A1BE垂直，则，
∴3a+12+3a=0，6a=﹣12，a=﹣2
∵0≤a≤3
∴不存在线段BC上存在点P，使平面A1DP与平面A1BE垂直
考点：向量语言表述面面的垂直、平行关系；直线与平面垂直的判定；用空间向量求直线与平面的夹角．
21. 如图，在四棱锥中，平面ABCD，，，E为CD的中点，M在AB上，且，

（1）求证：平面PAD；
（2）求平面PAD与平面PBC所成锐二面角的余弦值；
（3）点F是线段PD上异于两端点的任意一点，若满足异面直线EF与AC所成角为，求AF的长．
【答案】（1）证明见解析
（2）
（3）
【解析】
【分析】（1）由已知可得两两垂直，所以以为坐标原点，以所在的直线分别为轴建立空间直角坐标系，通过向量证明线线平行，再证明线面平行即可；
（2）分别求出相关平面的法向量后，再运用夹角公式计算即可；
（3）根据已知条件求出点的坐标，再计算长度即可．
【小问1详解】
证明：因为PA⊥平面ABCD，平面，所以，
因为，所以两两垂直，
所以以为坐标原点，以所在的直线分别为轴建立如图所示的空间直角坐标系，

因为，，E为CD的中点，M在AB上，且，
所以．
所以所以，
所以，又，所以，
又平面PAD，平面PAD，
所以平面PAD．
【小问2详解】
．
设平面的法向量为，
则有，可取，
由题意，平面的一个法向量可取，
设平面PAD与平面PBC所成锐二面角为，
则，
所以平面PAD与平面PBC所成锐二面角的余弦值为．
【小问3详解】
设，，
即，
可得，
所以，又，
由题意有，
化简得，解得或（舍），所以，
所以.