福建省厦门市第一中学2024-2025学年八年级上学期数学9月月考模拟试卷

展开

这是一份福建省厦门市第一中学2024-2025学年八年级上学期数学9月月考模拟试卷，共15页。

A．全B．面C．发D．展
2．（4分）如图，人字梯中间一般会设计一“拉杆”，这样做的道理是（）
A．三角形具有稳定性
B．垂线段最短
C．两点之间，线段最短
D．两直线平行，内错角相等
3．（4分）如图表示三角形的分类，则A表示的是（）
A．锐角三角形
B．直角三角形
C．钝角三角形
D．三边都不相等的三角形
4．（4分）在平面直角坐标系中，点P（﹣1，﹣2）关于x轴对称的点的坐标是（）
A．（﹣1，2）B．（2，﹣1）C．（﹣1，﹣2）D．（1，2）
5．（4分）如图，在△ABC中，过点A作AD⊥BC于点D，则下列说法正确的是（）
A．CD是△ABD的高
B．BD是△ADC的高
C．AD只是△ABC的高
D．AD是图中三个三角形的高
6．（4分）已知图中的两个三角形全等，则∠1等于（）
A．72°B．60°C．50°D．58°
7．（4分）已知△ABC，两个完全一样的三角板如图摆放，它们的一组对应直角边分别在AB，AC上，且这组对应边所对的顶点重合于点M，点M一定在（）
A．∠A的平分线上B．AC边的高上
C．BC边的垂直平分线上D．AB边的中线上
8．（4分）把一张正方形纸片按图对折两次后，再挖去一个小圆孔，那么展开后的图形应为（）
A．B．C．D．
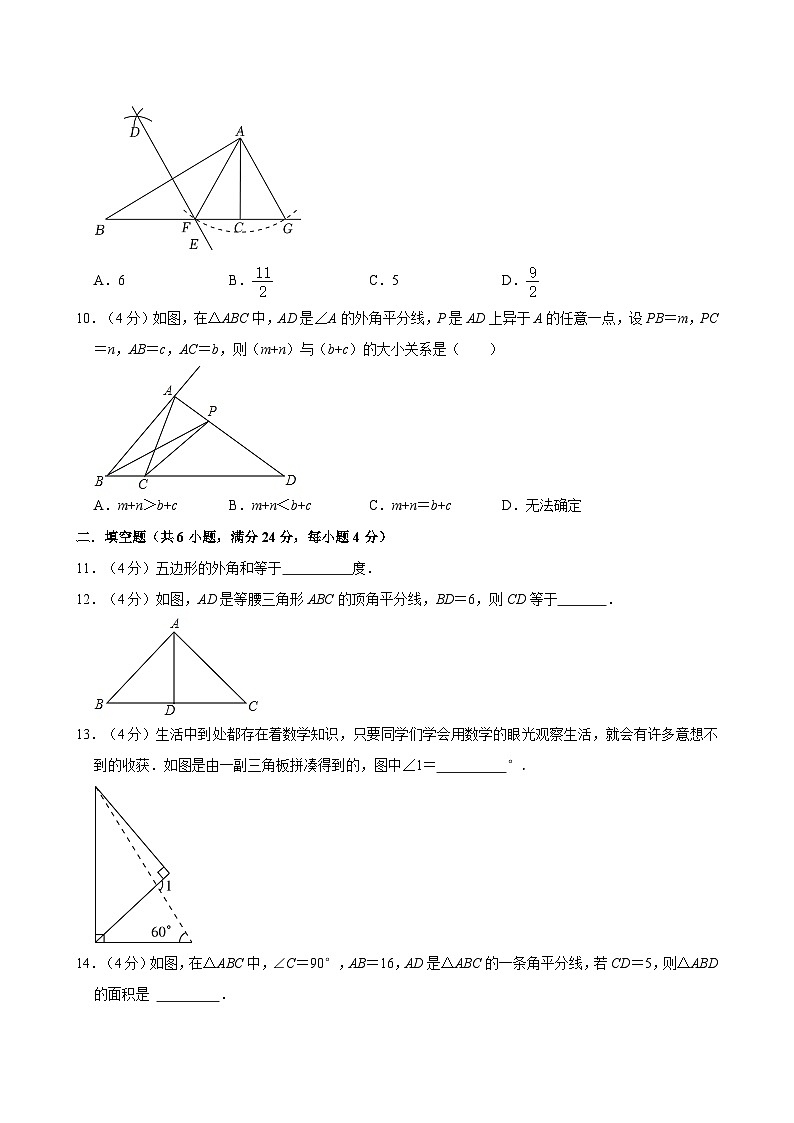
9．（4分）如图，在△ABC中，∠ACB＝90°，AC＜BC．分别以点A，B为圆心，大于AB的长为半径画弧，交于D，E两点，直线DE交BC于点F，连接AF．以点A为圆心，AF为半径画弧，交BC延长线于点G，连接AG．若△AFG的周长为9，则BC的长为（）
A．6B．C．5D．
10．（4分）如图，在△ABC中，AD是∠A的外角平分线，P是AD上异于A的任意一点，设PB＝m，PC＝n，AB＝c，AC＝b，则（m+n）与（b+c）的大小关系是（）
A．m+n＞b+cB．m+n＜b+cC．m+n＝b+cD．无法确定
二．填空题（共6小题，满分24分，每小题4分）
11．（4分）五边形的外角和等于度．
12．（4分）如图，AD是等腰三角形ABC的顶角平分线，BD＝6，则CD等于．
13．（4分）生活中到处都存在着数学知识，只要同学们学会用数学的眼光观察生活，就会有许多意想不到的收获．如图是由一副三角板拼凑得到的，图中∠1＝ °．
14．（4分）如图，在△ABC中，∠C＝90°，AB＝16，AD是△ABC的一条角平分线，若CD＝5，则△ABD的面积是．
15．（4分）如图，在△ABC中，若AB＝AC，AD＝BD，∠CAD＝24°，则∠C＝ °．
16．（4分）如图，在Rt△ABC中，AB＝10，BC＝8，AC＝6，∠C＝90°，将△ABC折叠，使其一边的两个端点重合，折痕为MN，则没有重合部分所成的三角形周长为．
三．解答题（共9小题，满分86分）
17．（8分）如图，AB＝AD，AC平分∠BAD．求证：△ABC≌△ADC．
18．（8分）作图题（要求：用尺规作图，保留作图痕迹，不写作法）
已知：如图，线段a，c，∠α．
求作：△ABC，使得BC＝a，AB＝c，∠ABC＝∠α．
19．（8分）如图，在△ABC中，AB＝AC，AD是△ABC的中线，DE∥AB．求证：△ADE是等腰三角形．
20．（8分）已知，如图，AD是BC的垂直平分线，DE⊥AB于点E，DF⊥AC于点F，
求证：（1）∠ABD＝∠ACD；
（2）DE＝DF．
21．（8分）如图，在边长为1个单位长度的10×8小正方形网格中，给出了以格点（网格线的交点）为顶点的△ABC，点A，C的坐标分别为（﹣3，2），（﹣1，3），直线l在网格线上．
（1）建立平面直角坐标系，画出△ABC关于直线l对称的△A1B1C1；（点A1，B1，C1分别为点A，B，C的对应点）
（2）若点P（a，b）是△ABC内任意一点，其关于直线l的对称点是P1，则点P1的坐标是．
22．（10分）（1）如图，用尺规作图的方法作出△ABC的角平分线AD．（保留作图痕迹，不要求写出作法）
（2）在（1）的基础上证明命题“全等三角形的对应角角平分线相等”是真命题．请填空并证明．
已知：如图，，AD和A'D'分别是∠BAC和∠B'AC'的平分线．
求证：．
证明：
23．（10分）在△ABC中，AB＝AC，∠BAC＝100°，点D在BC边上，△ABD和△AFD关于直线AD对称，∠FAC的平分线交BC于点G，连接FG．
（1）求∠DFG的度数；
（2）设∠BAD＝θ，
①当θ为何值时，△DFG为等腰三角形；
②△DFG有可能是直角三角形吗？若有，请求出相应的θ值；若没有，请说明理由．
24．（12分）如图，已知△ABC．
（1）用直尺和圆规作出△ABC的外角∠DAC的角平分线AP和BC边的垂直平分线MN（不写作法，保留作图痕迹）；
（2）在（1）的条件下，AP交MN于点E，EF⊥AC于点F，求证：AB+AC＝2CF．
25．（14分）已知O是四边形ABCD内一点，且OA＝OD，OB＝OC，∠AOD＝∠BOC．
（1）如图1，连接AC，BD，交点为G，连接OG，求证：①AC＝BD；
②OG平分∠DGC；
（2）如图2，若∠AOD＝∠BOC＝90°，E是CD的中点，过点O作OF⊥AB，垂足为F，
求证：点E，O，F在同一条直线上．
福建省厦门市第一中学2024-2025学年八年级上学期数学9月月考模拟试卷
参考答案与试题解析
一．选择题（共10小题，满分40分，每小题4分）
1．（4分）在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（）
A．全B．面C．发D．展
【答案】A
2．（4分）如图，人字梯中间一般会设计一“拉杆”，这样做的道理是（）
A．三角形具有稳定性
B．垂线段最短
C．两点之间，线段最短
D．两直线平行，内错角相等
【答案】A
3．（4分）如图表示三角形的分类，则A表示的是（）
A．锐角三角形
B．直角三角形
C．钝角三角形
D．三边都不相等的三角形
【答案】D
4．（4分）在平面直角坐标系中，点P（﹣1，﹣2）关于x轴对称的点的坐标是（）
A．（﹣1，2）B．（2，﹣1）C．（﹣1，﹣2）D．（1，2）
【答案】A
5．（4分）如图，在△ABC中，过点A作AD⊥BC于点D，则下列说法正确的是（）
A．CD是△ABD的高
B．BD是△ADC的高
C．AD只是△ABC的高
D．AD是图中三个三角形的高
【答案】D
6．（4分）已知图中的两个三角形全等，则∠1等于（）
A．72°B．60°C．50°D．58°
【答案】D
7．（4分）已知△ABC，两个完全一样的三角板如图摆放，它们的一组对应直角边分别在AB，AC上，且这组对应边所对的顶点重合于点M，点M一定在（）
A．∠A的平分线上B．AC边的高上
C．BC边的垂直平分线上D．AB边的中线上
【答案】A
8．（4分）把一张正方形纸片按图对折两次后，再挖去一个小圆孔，那么展开后的图形应为（）
A．B．C．D．
【答案】C
9．（4分）如图，在△ABC中，∠ACB＝90°，AC＜BC．分别以点A，B为圆心，大于AB的长为半径画弧，交于D，E两点，直线DE交BC于点F，连接AF．以点A为圆心，AF为半径画弧，交BC延长线于点G，连接AG．若△AFG的周长为9，则BC的长为（）
A．6B．C．5D．
【答案】D
10．（4分）如图，在△ABC中，AD是∠A的外角平分线，P是AD上异于A的任意一点，设PB＝m，PC＝n，AB＝c，AC＝b，则（m+n）与（b+c）的大小关系是（）
A．m+n＞b+cB．m+n＜b+cC．m+n＝b+cD．无法确定
【答案】A
二．填空题（共6小题，满分24分，每小题4分）
11．（4分）五边形的外角和等于 360 度．
【答案】见试题解答内容
12．（4分）如图，AD是等腰三角形ABC的顶角平分线，BD＝6，则CD等于 6 ．
【答案】6．
13．（4分）生活中到处都存在着数学知识，只要同学们学会用数学的眼光观察生活，就会有许多意想不到的收获．如图是由一副三角板拼凑得到的，图中∠1＝ 105 °．
【答案】105．
14．（4分）如图，在△ABC中，∠C＝90°，AB＝16，AD是△ABC的一条角平分线，若CD＝5，则△ABD的面积是 40 ．
【答案】40．
15．（4分）如图，在△ABC中，若AB＝AC，AD＝BD，∠CAD＝24°，则∠C＝ 52 °．
【答案】52．
16．（4分）如图，在Rt△ABC中，AB＝10，BC＝8，AC＝6，∠C＝90°，将△ABC折叠，使其一边的两个端点重合，折痕为MN，则没有重合部分所成的三角形周长为 18或16或14 ．
【答案】18或16或14．
三．解答题（共9小题，满分86分）
17．（8分）如图，AB＝AD，AC平分∠BAD．求证：△ABC≌△ADC．
【答案】证明过程见解答．
18．（8分）作图题（要求：用尺规作图，保留作图痕迹，不写作法）
已知：如图，线段a，c，∠α．
求作：△ABC，使得BC＝a，AB＝c，∠ABC＝∠α．
【答案】作图见解答过程．
19．（8分）如图，在△ABC中，AB＝AC，AD是△ABC的中线，DE∥AB．求证：△ADE是等腰三角形．
【答案】见试题解答内容
20．（8分）已知，如图，AD是BC的垂直平分线，DE⊥AB于点E，DF⊥AC于点F，
求证：（1）∠ABD＝∠ACD；
（2）DE＝DF．
【答案】见试题解答内容
21．（8分）如图，在边长为1个单位长度的10×8小正方形网格中，给出了以格点（网格线的交点）为顶点的△ABC，点A，C的坐标分别为（﹣3，2），（﹣1，3），直线l在网格线上．
（1）建立平面直角坐标系，画出△ABC关于直线l对称的△A1B1C1；（点A1，B1，C1分别为点A，B，C的对应点）
（2）若点P（a，b）是△ABC内任意一点，其关于直线l的对称点是P1，则点P1的坐标是（﹣a+2，b）．
【答案】（1）见解答；
（2）（﹣a+2，b）．
22．（10分）（1）如图，用尺规作图的方法作出△ABC的角平分线AD．（保留作图痕迹，不要求写出作法）
（2）在（1）的基础上证明命题“全等三角形的对应角角平分线相等”是真命题．请填空并证明．
已知：如图， △ABC≌△A′B′C′ ，AD和A'D'分别是∠BAC和∠B'AC'的平分线．
求证： AD＝A′D′ ．
证明：
【答案】（1）见解析；（2）△ABC≌△A′B′C′，AD＝A′D′，证明见解析．
23．（10分）在△ABC中，AB＝AC，∠BAC＝100°，点D在BC边上，△ABD和△AFD关于直线AD对称，∠FAC的平分线交BC于点G，连接FG．
（1）求∠DFG的度数；
（2）设∠BAD＝θ，
①当θ为何值时，△DFG为等腰三角形；
②△DFG有可能是直角三角形吗？若有，请求出相应的θ值；若没有，请说明理由．
【答案】见试题解答内容
24．（12分）如图，已知△ABC．
（1）用直尺和圆规作出△ABC的外角∠DAC的角平分线AP和BC边的垂直平分线MN（不写作法，保留作图痕迹）；
（2）在（1）的条件下，AP交MN于点E，EF⊥AC于点F，求证：AB+AC＝2CF．
【答案】（1）作图见解答；
（2）证明过程见解答．
25．（14分）已知O是四边形ABCD内一点，且OA＝OD，OB＝OC，∠AOD＝∠BOC．
（1）如图1，连接AC，BD，交点为G，连接OG，求证：①AC＝BD；
②OG平分∠DGC；
（2）如图2，若∠AOD＝∠BOC＝90°，E是CD的中点，过点O作OF⊥AB，垂足为F，
求证：点E，O，F在同一条直线上．
【答案】（1）①证明见解答；
②证明见解答；
（2）证明见解答．