

冀教版(2024)七年级上册(2024)1.1 正数和负数教案及反思
展开课时目标
1.经历从现实生活中的实例引出负数的过程,体会数学与现实生活的联系,发展学生的抽象能力与符号意识.
2.通过用带“+”或“-”的数表示生活中具有相反意义的量,知道具有相反意义的量之间的关系,发展学生的数感.
学习重点
理解具有相反意义的量.
学习难点
用带“+”或“-”的数表示具有相反意义的量.
课时活动设计
情境引入
观察下列图片,体会这些数是怎么产生和发展的.
想一想:这些数足以表示我们生活中的量吗?
设计意图:让学生体会数的出现是现实生活的需要,发展学生的数感和符号意识,为本节课的学习作铺垫,同时也让学生体会到数学来源于生活而又服务于生活,提高学生的学习兴趣.
探究新知
探究1 具有相反意义的量
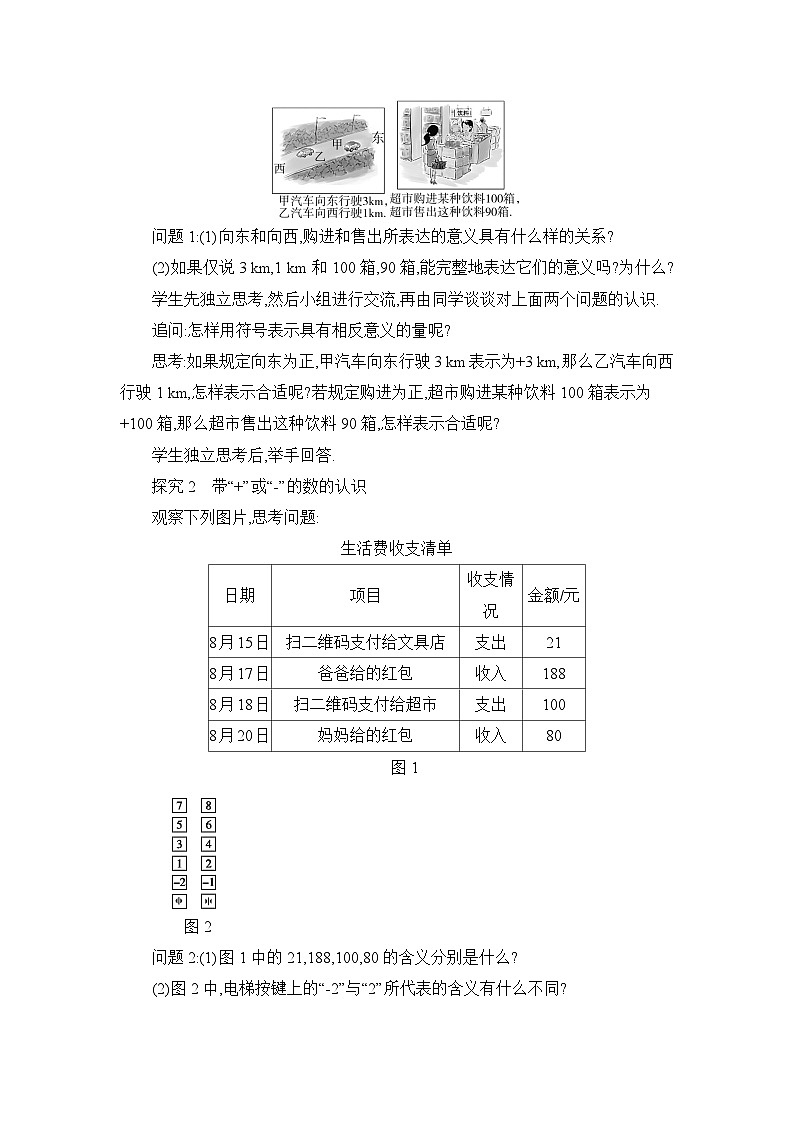
观察下列图片,并思考用什么数表示.
问题1:(1)向东和向西,购进和售出所表达的意义具有什么样的关系?
(2)如果仅说3 km,1 km和100箱,90箱,能完整地表达它们的意义吗?为什么?
学生先独立思考,然后小组进行交流,再由同学谈谈对上面两个问题的认识.
追问:怎样用符号表示具有相反意义的量呢?
思考:如果规定向东为正,甲汽车向东行驶3 km表示为+3 km,那么乙汽车向西行驶1 km,怎样表示合适呢?若规定购进为正,超市购进某种饮料100箱表示为+100箱,那么超市售出这种饮料90箱,怎样表示合适呢?
学生独立思考后,举手回答.
探究2 带“+”或“-”的数的认识
观察下列图片,思考问题:
生活费收支清单
图1
图2
问题2:(1)图1中的21,188,100,80的含义分别是什么?
(2)图2中,电梯按键上的“-2”与“2”所代表的含义有什么不同?
(3)怎样用符号表示这些具有相反意义的量呢?
学生先独立思考,然后举手回答问题.
教师引导学生总结出具有相反意义的量的特点:一般地,对于具有相反意义的量,我们可以把其中一种意义的量规定为正的,并在表示这个量的数的前面加上“+”(读作“正”)来表示;把与它意义相反的量规定为负的,并在表示这个量的数的前面加上“-”(读作“负”)来表示.
探究3 带“+”或“-”的数的应用
做一做:
1.请仿照上述表示相反意义的量的方法,完成下表:
2.用带“+”或“-”的数表示下列具有相反意义的量:
(1)如果规定高于海平面记作正,那么,珠穆朗玛峰高于海平面8 848.86 m,可记作 -8 848.86 m,吐鲁番盆地最低点低于海平面154.31 m,可记作 -154.31 m.
(2)如果规定收入记作正,那么,小亮家的年收入126 800元可记作 +126 800 元;“-77 800元”表示小亮家 支出 (填“收入”或“支出”)了77 800元.
学生先独立思考,然后小组交流展评.
追问:你能举出现实生活中还可以用带“+”或“-”的数表示的具有相反意义的量吗?
设计意图:让学生体会用符号表示数的简洁性,培养学生的符号意识.通过生活中的实例,让学生体会类比的数学思想方法,增强处理信息的能力,引导学生用带“+”或“-”的数来表示具有相反意义的量,培养学生的抽象概括能力,同时突破本节课的难点,培养学生的符号意识.
典例精讲
例 有一批白菜,以每筐25 kg为准,现抽取8筐样品进行称重,称后的记录如下(单位:kg):
26.5,22,27,24.5,26,23,23,22.5.
如果规定超过标准质量的部分记作正,请分别用带“+”或“-”的数表示样品质量与标准质量的差.
解:由题意,得这8筐样品质量与标准质量的差表示为+1.5 kg,-3 kg,+2 kg,-0.5 kg,+1 kg,-2 kg,-2 kg,-2.5 kg.
设计意图:通过例题,提高学生运用知识的能力和推理能力,加深学生用带“+”或“-”的数表示具有相反意义的量的理解与应用.
巩固训练
1.下列选项中,表示的不是一对具有相反意义的量的是(D)
A.超市购进30千克葡萄和卖出30千克葡萄
B.电梯上升10米和下降10米
C.高于警戒水位0.6米和低于警戒水位0.6米
D.年龄增加2岁和体重减少2千克
2.如果盈利50元记作+50元,那么亏损30元记作(C)
A.+30元 B.-20元 C.-30元 D.+20元
3.某地冬季里某一天的气温为-3℃,“-3℃”的含义是(A)
A.零下3摄氏度 B.零上3摄氏度
C.降低3摄氏度 D.升高3摄氏度
4.在体育课立定跳远测试中,以2.00 m为标准,若小明跳出了2.35 m,可记作+0.35 m,则小刚跳出了1.65 m,应记作 -0.35 m .
设计意图:通过设置不同形式的练习题,使学生所学知识得到巩固,也使学生的思维能力得到提高,能更好地将知识学以致用.
课堂小结
本节课我们研究用带“+”或“-”的数表示具有相反意义的量,请同学们带着以下问题进行总结:
(1)数是如何产生的?“+”或“-”可以表示生活中的哪些量?
(2)在学习用带“+”或“-”的数表示具有相反意义的量的过程中,你经历了什么?这个过程中用到了哪些数学方法?积累了哪些活动经验?
设计意图:学生通过自主反思,可进一步加深对具有相反意义的量的理解,通过运用数学思想解决问题,培养学生的数学思维品质,让学生学会学习,学会思考,使学生真正深入数学学习过程中,抓住数学思维的内在实质.
课堂8分钟.
1.教材第4,5页习题A组第1,2题,B组第3题.
2.七彩作业.
教学反思
第2课时 有理数的分类
课时目标
1.通过具有相反意义的量的表示方法,引导学生理解正、负数的概念,会识别正、负数,培养学生的数感与符号意识.
2.了解有理数的概念,掌握有理数的分类方法,会将有理数恰当归类,体会分类讨论的数学思想方法,培养学生的数感.
学习重点
理解有理数的概念,并能掌握有理数的分类.
学习难点
熟练准确地进行有理数的分类.
课时活动设计
复习引入
上节课我们学习了用带“+”或“-”的数表示具有相反意义的量,请举例说明.
学生先独立思考,然后请同学回答.
例如:+2,-3,+8,-13,+20,-6,+290,-123,-53,+22,-43…
追问:观察这些数,它们有什么特征?你能将它们进行分类吗?
设计意图:引导学生回顾上一节所学内容,让学生进行分类,体会分类讨论的数学思想方法,培养学生的抽象意识.
探究新知
探究1 正、负数的概念
思考:经过观察上一活动中的数,可以发现,它们都是在之前学过的数前面加上“+”或“-”得到的,你能尝试给这样的数下个定义吗?
学生先独立思考,然后小组交流,最后由各组尝试给出定义,教师适当做出引导.
师生共同归纳正、负数的概念:像-3,-13,-6,-123,-53,-43等这样形式的数,它们都是在已学过的数(0除外)的前面加上“-”得到的,这样的数叫作负数;像+2,+8,+20,+290,+22等这样形式的数,都是在已学过的数(0除外)的前面加上“+”得到的,这样的数叫作正数.
0既不是正数也不是负数.正数中的“+”可以省略不写,如+2可以写成2,等等.
思考:(1)“-”为什么不能省略不写呢?
(2)结合小学学过的各种数,请任意写出10个正数,10个负数(形式尽量多样).
学生先独立思考,然后小组讨论,最后展评.
探究2 有理数的认识及分类
教师将学生举出的正数和负数的例子写在黑板上,例如:
正数:+7,13,998,4,70,+1.8%,16,+17,3.8,+711.
负数:-9,-4.5,-910,-4,-2,-2.7%,-8,-2.7,-43.
思考:你能将上述正、负数再进行分类吗?说一说你分类的依据.
学生分类,教师同步展示:
正整数:+7,998,4,70,+17;
正分数:13,+1.8%,16,3.8,+711;
负整数:-9,-4,-2,-8;
负分数:-4.5,-910,-2.7%,-2.7,-43.
教师归纳总结:正整数、0和负整数统称为整数,正分数和负分数统称为分数,整数和分数统称为有理数.
任何分数都可以化为有限小数或无限循环小数;反过来,任何有限小数或无限循环小数都能表示成分数.例如:3.8=(3.8×10)÷10=3810=195.
设计意图:引导学生对数进行分类,并概括正、负数的概念,培养学生的抽象概括能力和分类意识,培养学生的发散思维,为进一步的分类作准备,发展学生的数感和符号意识.通过对数进行分类,培养学生科学严谨的态度,让学生知道分类要做到不重不漏,体会分类讨论的数学思想方法,培养学生的数感与抽象能力.
典例精讲
例1 读出下列各数,并把它们分别填入相应的圈内:
-8,16,+7,-2.7,-43,3.8,+711,0.
正数: 负数:
整数: 负分数:
解:正数有16,+7,3.8,+711;负数有-8,-2.7,-43;
整数有-8,+7,0;负分数有-2.7,-43.
例2 (1)整数、负数有什么特点?
(2)一个数不是正数就是负数,对吗?
(3)下面的数是什么数?
13,25,112,0.2,4.25.
解:(1)整数包括正整数、0和负整数.负数包括负整数和负分数.
(2)不对.0既不是正数,也不是负数.0是正数与负数的分界.
(3)分数和小数,统称为分数.
教师提示:小学阶段的分数和小数在初中阶段统称为分数.
设计意图:通过例题,提高学生运用知识的能力,增强学生对数的分类意识,加深学生对有理数及其分类的理解与应用.
巩固训练
1.关于-4,227,0.41,-116,0,3.14这六个数,下列说法错误的是(B)
A.-4,0是整数
B.227,0.41,0,3.14是正数
C.-4,227,0.41,-116,0,3.14是有理数
D.-4,-116是负数
2.下列说法正确的是(A)
A.自然数就是非负整数 B.正数和负数统称为有理数
C.整数一定是正数 D.分数包括正分数、负分数和0
3.某种试剂的说明书上标明保存温度是(10±2)℃,请你写出一个适合该试剂保存的温度: 9℃(答案不唯一,在8~12℃范围内即可) .
设计意图:通过设置不同层次的练习,不仅能使学生的新知得到及时巩固,也使学生的思维能力得到有效提高,能更好地将知识学以致用.
课堂小结
本节课我们研究了正数和负数及有理数的概念,请同学们带着以下问题进行总结:
(1)有理数有几种分类方法?分别是什么?
(2)在学习有理数的过程中,你经历了什么?这个过程中用到了哪些数学方法?积累了哪些活动经验?
设计意图:学生通过自主反思,可进一步加深对正、负数及有理数概念的理解,通过反思数学思想方法与活动经验,培养学生的数学思维品质,让学生学会学习,学会思考,使学生真正深入数学学习过程中,抓住数学思维的内在实质.
课堂8分钟.
1.教材第7,8页习题A组第2题,B组第4,5题,C组第6题选做.
2.七彩作业.
教学反思
日期
项目
收支情况
金额/元
8月15日
扫二维码支付给文具店
支出
21
8月17日
爸爸给的红包
收入
188
8月18日
扫二维码支付给超市
支出
100
8月20日
妈妈给的红包
收入
80
意义
向北走1.8 km
向南走3 km
盈利30%
亏损20%
水位上升
30 cm
水位
下降
50 cm
表示方法
+1.8 km
-3 km
+30%
-20%
+30 cm
-50 cm
数学七年级上册(2024)1.1 正数和负数教案: 这是一份数学七年级上册(2024)<a href="/sx/tb_c4050844_t8/?tag_id=27" target="_blank">1.1 正数和负数教案</a>,共5页。
2021学年第一章 有理数1.1 正数和负数教案: 这是一份2021学年第一章 有理数1.1 正数和负数教案,共9页。教案主要包含了课时安排,第一课时,教学目标,教学重难点,教学准备,教学过程,教法说明,第二课时等内容,欢迎下载使用。
数学七年级上册1.1 正数和负数教案: 这是一份数学七年级上册1.1 正数和负数教案,共13页。教案主要包含了具有相反意义的量的表示方法,观察归纳,巩固训练,应用迁移,拓展升华,学习总结等内容,欢迎下载使用。













