08 第46讲　空间距离及立体几何中的探索性问题 【正文】作业 高考数学二轮复习练习

这是一份08 第46讲　空间距离及立体几何中的探索性问题 【正文】作业 高考数学二轮复习练习，共5页。
1.[2023·湖南衡阳模拟] 已知平面α的一个法向量为n=(-2,-2,1),点A(-1,3,0)在α内,则P(-2,1,4)到α的距离为( )
A.10B.3
C.83D.103
2.在空间直角坐标系中,已知A(1,-1,1),B(3,1,1),则点P(1,0,2)到直线AB的距离为( )
A.22B.32
C.62D.3
3.已知正三棱柱ABC-A1B1C1的所有棱长都为2,则B1C1到平面A1BC的距离是( )
A.217B.2217
C.3217D.4217
4.已知点A(1,0,0),B(0,1,0),C(0,0,2),P(1,-1,0),那么过点P且平行于平面ABC的平面与平面ABC间的距离是( )
A.2B.22
C.23D.14
5.已知点A(2,1,1)是直线l上一点,a=(1,0,0)是直线l的一个方向向量,则点P(1,2,0)到直线l的距离是 .
6.[2023·重庆一中模拟] 在空间直角坐标系中,一个四面体的四个顶点坐标分别为(1,2,3),(4,1,5),(2,3,4),(6,6,1),则其体积为 .
7.已知边长为4的正方形ABCD所在平面外一点P与正方形的中心O的连线PO垂直于平面ABCD,且PO=6,则PO的中点M到△PBC的重心N的距离为( )
A.53B.43
C.23D.12
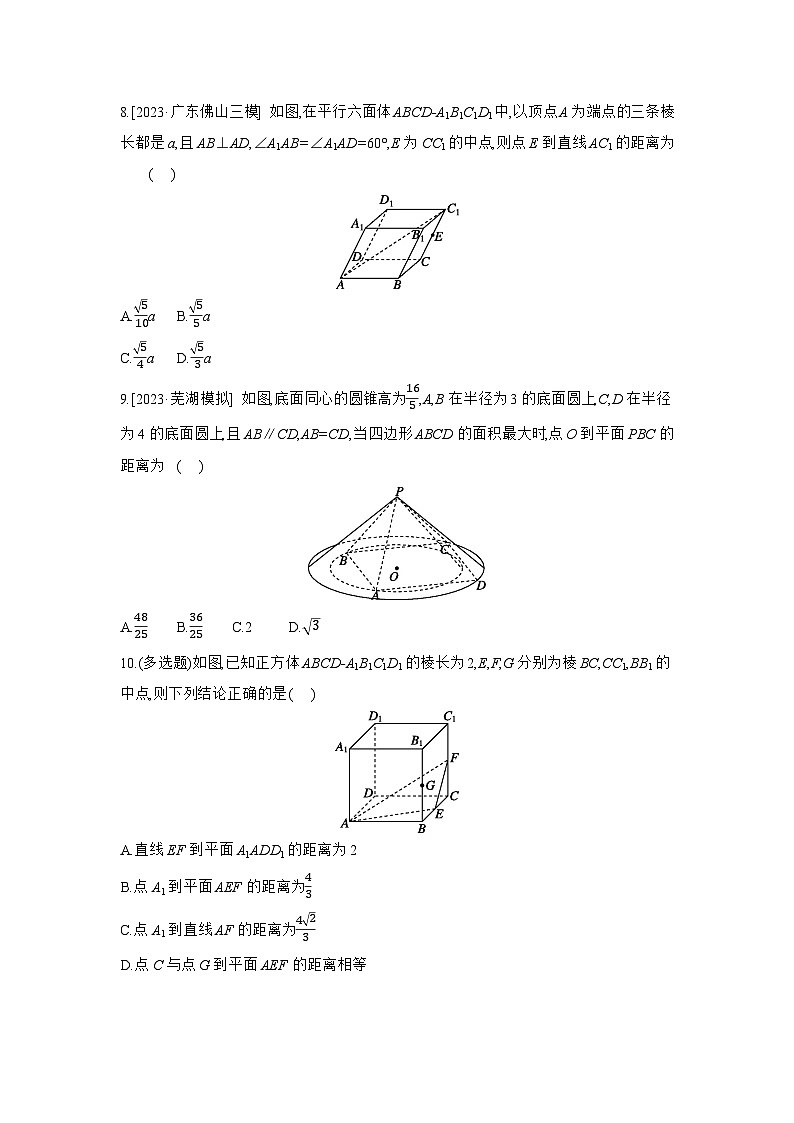
8.[2023·广东佛山三模] 如图,在平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都是a,且AB⊥AD,∠A1AB=∠A1AD=60°,E为CC1的中点,则点E到直线AC1的距离为( )
A.510aB.55a
C.54aD.53a
9.[2023·芜湖模拟] 如图,底面同心的圆锥高为165,A,B在半径为3的底面圆上,C,D在半径为4的底面圆上,且AB∥CD,AB=CD,当四边形ABCD的面积最大时,点O到平面PBC的距离为( )
A.4825B.3625C.2D.3
10.(多选题)如图,已知正方体ABCD-A1B1C1D1的棱长为2,E,F,G分别为棱BC,CC1,BB1的中点,则下列结论正确的是( )
A.直线EF到平面A1ADD1的距离为2
B.点A1到平面AEF的距离为43
C.点A1到直线AF的距离为423
D.点C与点G到平面AEF的距离相等
11.(多选题)[2023·河北邯郸一模] 在棱长为6的正方体ABCD-A1B1C1D1中,E为A1B1的中点,P在棱BC上(不包括端点),则下列判断正确的是( )
A.存在点P,使得AP⊥平面DD1E
B.存在点P,使得三棱锥P-DD1E的体积为45
C.存在点P,使得点P到DE的距离为5
D.当P为BC的中点时,三棱锥P-DD1E的外接球的表面积为86π
12.在空间直角坐标系中,已知A(a2,2a,6),B(0,0,1),C(1,1,2),D(-1,0,3),E(a2,0,5),则当点A到平面BCD的距离最小时,直线AE与平面BCD所成角的正弦值为 .
13.如图,在四棱锥S-ABCD中,底面ABCD是矩形,AD=SA=SD=2AB=2,P为棱AD的中点,且SP⊥AB,AM=λAS(0≤λ≤1),若点M到平面SBC的距离为33,则实数λ的值为 .
14.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BB1的中点.
(1)证明:BC1∥平面AD1E;
(2)求直线BC1到平面AD1E的距离.
15.[2023·浙江宁波三模] 如图①,在直角梯形ABCD中,CD⊥AD,AB=BC=2CD=2,AD=3,现将△ACD沿着对角线AC折起,使点D到达点P的位置(如图②),此时二面角P-AC-D的大小为π3.
(1)求异面直线PA与BC所成角的余弦值;
(2)求点A到平面PBC的距离.
关注公众号《全元高考》
微信搜索微信公众号「全元高考」
后台回复「网盘群」获取最新最全初高中网盘资源（4000 G+）
扫码加微信查看朋友圈最新资源
备用联系方式QQ：2352064664
群文件全套无水印资料+更多精品网课在网盘群，高考路上必备!
最新最全高一高二高三试卷&九科全新一手网课&学科资料专辑&名校独家资料
更新速度极快!
进群了就不用到处找资料了，一网打尽!
(进群送往届全部资料)
16.如图所示,在四棱锥S-ABCD中,底面ABCD是边长为2的正方形,SA⊥平面ABCD,二面角S-DC-A的大小为π4,E,F,G分别是SA,SB,BC的中点.
(1)求证:SD∥平面EFG.
(2)在棱BC上是否存在一点M,使得点A到平面EFM的距离为45?若存在,求出BMMC的值;若不存在,请说明理由.