2019-2020学年江苏省盐城市九年级上学期数学期末试题及答案

这是一份2019-2020学年江苏省盐城市九年级上学期数学期末试题及答案，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.一元二次方程的根是（ ）
A. B.
C. D.
【答案】D
【解析】
x2−3x=0，
x(x−3)=0，
∴x1=0，x2=3.
故选D.
2.如图，是的外接圆，是直径．若，则等于（ ）
A. B. C. D.
【答案】C
【解析】
【分析】
根据同弧所对的圆周角等于圆心角的一半可得：∠A= ∠BOC=40°．
【详解】∵∠BOC=80°，
∴∠A=∠BOC=40°．
故选C．
【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
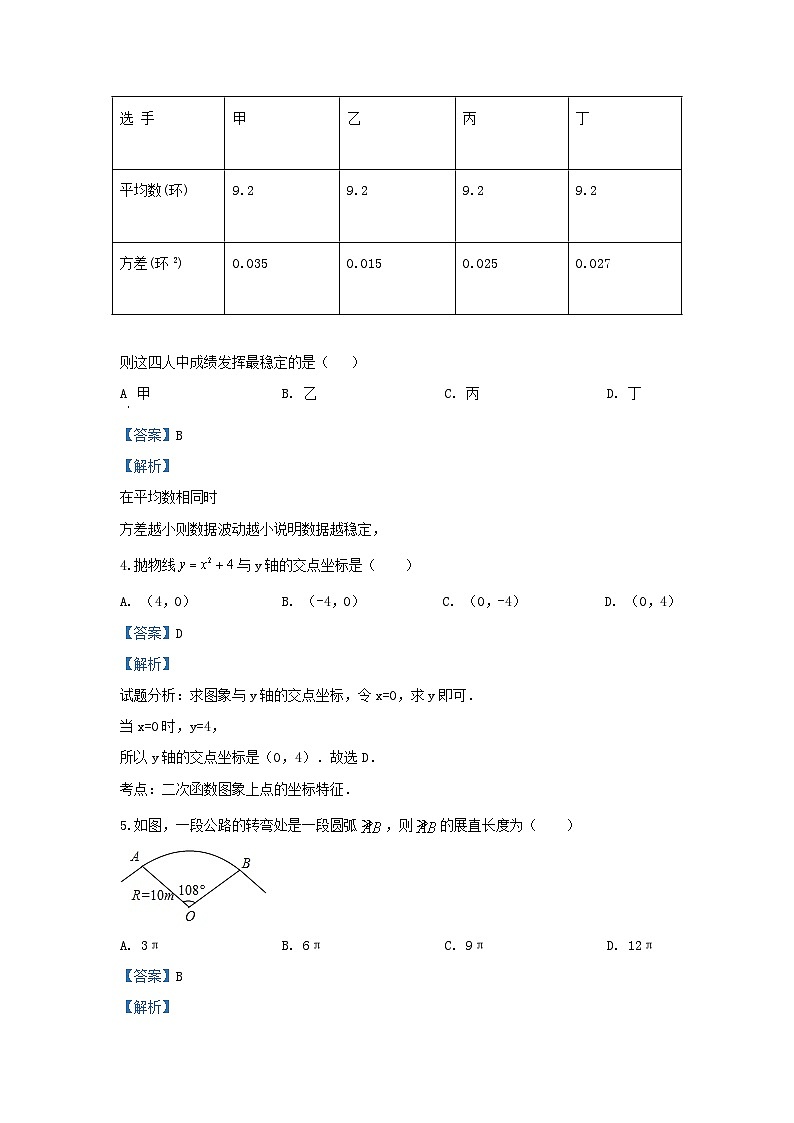
3.甲、乙、丙、丁四位选手各10次射击成绩的平均数和方差如下表：
则这四人中成绩发挥最稳定的是（ ）
A 甲B. 乙C. 丙D. 丁
【答案】B
【解析】
在平均数相同时
方差越小则数据波动越小说明数据越稳定，
4.抛物线与y轴的交点坐标是（ ）
A. （4，0）B. （-4，0）C. （0，-4）D. （0，4）
【答案】D
【解析】
试题分析：求图象与y轴的交点坐标，令x=0，求y即可．
当x=0时，y=4，
所以y轴的交点坐标是（0，4）．故选D．
考点：二次函数图象上点的坐标特征．
5.如图，一段公路的转弯处是一段圆弧，则的展直长度为（ ）
A. 3πB. 6πC. 9πD. 12π
【答案】B
【解析】
分析：直接利用弧长公式计算得出答案．
详解：的展直长度为：=6π（m）．
故选B．
点睛：此题主要考查了弧长计算，正确掌握弧长公式是解题关键．
6.如图，在中，，，，则
A. B. C. D.
【答案】A
【解析】
【分析】
先利用勾股定理求出斜边AB，再求出sinB即可．
【详解】∵在中，，，，
∴，
∴.
故答案为A.
【点睛】本题考查的知识点是锐角三角函数的定义，解题关键是熟记三角函数的定义.
7.两三角形的相似比是2：3，则其面积之比是（ ）
A. ：B. 2：3C. 4：9D. 8：27
【答案】C
【解析】
【分析】根据相似三角形的面积比等于相似比的平方计算即可．
【详解】∵两三角形的相似比是2：3，
∴其面积之比是4：9，
故选C．
【点睛】本题考查了相似三角形的性质，熟练掌握相似三角形的面积比等于相似比的平方是解题的关键.
8.将抛物线y=﹣5x2+1向左平移1个单位长度，再向下平移2个单位长度，所得到的抛物线为（ ）
A. y=﹣5（x+1）2﹣1B. y=﹣5（x﹣1）2﹣1C. y=﹣5（x+1）2+3D. y=﹣5（x﹣1）2+3
【答案】A
【解析】
分析：直接利用二次函数图象与几何变换的性质分别平移得出答案．
详解：将抛物线y=-5x2+1向左平移1个单位长度，得到y=-5（x+1）2+1，再向下平移2个单位长度，
所得到的抛物线为：y=-5（x+1）2-1．
故选A．
点睛：此题主要考查了二次函数图象与几何变换，正确记忆平移规律是解题关键．
二、填空题（本大题共8小题，每小题3分，共24分）
9.当_____时，是关于的一元二次方程.
【答案】
【解析】
【分析】
根据一元二次方程的定义得到m−1≠0，解不等式即可．
【详解】解：∵方程是关于x一元二次方程，
∴m−1≠0，
∴m≠1，
故答案为：.
【点睛】本题考查了一元二次方程的定义：只含有一个未知数，并且未知数的最高次数为2的整式方程叫一元二次方程．
10.在本赛季比赛中，某运动员最后六场的得分情况如下：17、15、21、28、12、19，则这组数据的方差为______.
【答案】.
【解析】
【分析】
先计算出这组数据的平均数，然后根据方差公式求解．
【详解】解：平均数=
所以方差是S2=

=
故答案为：.
【点睛】本题考查方差：一般地设n个数据，x1，x2，…xn的平均数为，则方差
S2= ,它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
11.有一个能自由转动的转盘如图，盘面被分成8个大小与性状都相同的扇形，颜色分为黑白两种，将指针的位置固定，让转盘自由转动，当它停止后，指针指向白色扇形的概率是 ．
【答案】
【解析】
【详解】解：∵每个扇形大小相同，因此阴影面积与空白的面积相等，
∴落在白色扇形部分的概率为：=．
故答案为．
考点：几何概率
12.若二次函数的图象与x轴只有一个公共点，则实数n=______．
【答案】4．
【解析】
】解：y=x2﹣4x+n中，a=1，b=﹣4，c=n，b2﹣4ac=16﹣4n=0，解得n=4．故答案为4．
13.若是一元二次方程的两个实数根，则_______．
【答案】1
【解析】
【分析】
利用一元二次方程根与系数的关系求出，即可求得答案．
【详解】∵是一元二次方程的两个实数根，
∴，，
∴，
故答案为：1.
【点睛】本题主要考查了一元二次方程根与系数的关系，方程的两个根为，则，.
14.如图，中，，则 __________．
【答案】17
【解析】
∵Rt△ABC中，∠C=90°，∴tanA= ，
∵，∴AC＝8，
∴AB= =17,
故答案17.
15.如图，三个顶点的坐标分别为，以原点O为位似中心，把这个三角形缩小为原来的，可以得到，已知点的坐标是，则点的坐标是______.
【答案】（1，2）
【解析】
解：∵点A的坐标为（2，4），以原点O为位似中心，把这个三角形缩小为原来的，∴点A′的坐标是（2×，4×），即（1，2）．故答案为（1，2）．
16.已知⊙半径为，点在⊙上，，则线段的最大值为_____．
【答案】
【解析】
【分析】
过点A作AE⊥AO,并使∠AEO＝∠ABC,先证明，由三角函数可得出，进而求得，再通过证明，可得出，根据三角形三边关系可得:,由勾股定理可得，求出BE的最大值，则答案即可求出.
【详解】解:过点A作AE⊥AO,并使∠AEO＝∠ABC,
∵ ,
∴,
∴
∵,
∴,
∴,
∴，
又∵,
∴,
∵，
∴ ，
又∵，
∴,
∴,
∴,
在△OEB中，根据三角形三边关系可得:,
∵，
∴,
∴BE的最大值为：，
∴OC的最大值为：.
【点睛】本题主要考查了三角形相似的判定和性质、三角函数、勾股定理及三角形三边关系，解题的关键是构造直角三角形.
三、解答题（本大题共102分）
17.解方程：
【答案】,
【解析】
【分析】
先把移到等号右边，然后再两边直接开平方即可.
【详解】
,
【点睛】本题主要考查了直接开平方法解一元二次方程，做题时注意不要漏解.
18.求值：
【答案】2.
【解析】
【分析】
先将三角函数值代入，再根据混合运算顺序依此计算可得.
【详解】原式＝
【点睛】本题主要考查了特殊角的三角函数值，解题的关键是熟练掌握各特殊角的三角函数值.
19.国家规定，中、小学生每天在校体育活动时间不低于1h．为此，某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生．根据调查结果绘制成的统计图如图所示，其中A组为t＜0.5h，B组为0.5h≤t＜1h，C组为1h≤t＜1.5h，D组为t≥1.5h．
请根据上述信息解答下列问题：
（1）本次调查数据的众数落在 组内，中位数落在 组内；
（2）该辖区约有18000名初中学生，请你估计其中达到国家规定体育活动时间的人数．
【答案】（1）B，C；（2）960．
【解析】
【分析】
（1）根据中位数的概念，中位数应是第150、151人时间的平均数，分析可得答案；
（2）首先计算样本中达到国家规定体育活动时间的频率，再进一步估计总体达到国家规定体育活动时间的人数．
【详解】（1）众数在B组．
根据中位数的概念，中位数应是第150、151人时间的平均数，分析可得其均在C组，故本次调查数据的中位数落在C组．
故答案为B，C；
（2）达国家规定体育活动时间的人数约1800×=960（人）．
答：达国家规定体育活动时间的人约有960人．
考点：频数（率）分布直方图；用样本估计总体；中位数；众数．
20.为了维护国家主权和海洋权利，海监部门对我国领海实现了常态化巡航管理，如图，正在执行巡航任务的海监船以每小时50海里的速度向正东方航行，在A处测得灯塔P在北偏东60°方向上，继续航行1小时到达B处，此时测得灯塔P在北偏东30°方向上．
（1）求∠APB的度数；
（2）已知在灯塔P的周围25海里内有暗礁，问海监船继续向正东方向航行是否安全？
．
【答案】（1）30°；（2）海监船继续向正东方向航行是安全的．
【解析】
【分析】
（1）根据直角的性质和三角形的内角和求解；
（2）过点P作PH⊥AB于点H，根据解直角三角形，求出点P到AB的距离，然后比较即可.
【详解】解：（1）在△APB中，∠PAB=30°，∠ABP=120°
∴∠APB=180°-30°-120°=30°
（2）过点P作PH⊥AB于点H

在Rt△APH中，∠PAH=30°，AH=PH
在Rt△BPH中，∠PBH=30°，BH=PH
∴AB=AH-BH=PH=50
解得PH=25＞25，因此不会进入暗礁区，继续航行仍然安全.
考点：解直角三角形
21.一个盒子里有标号分别为1，2，3，4的四个球，这些球除标号数字外都相同．
(1)从盒中随机摸出一个小球，求摸到标号数字为奇数的球的概率；
(2)甲、乙两人用这四个小球玩摸球游戏，规则是：甲从盒中随机摸出一个小球，记下标号数字后放回盒里，充分摇匀后，乙再从盒中随机摸出一个小球，并记下标号数字．若两次摸到球的标号数字同为奇数或同为偶数，则判甲赢；若两次摸到球的标号数字为一奇一偶，则判乙赢．请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平．
【答案】(1)；(2) 这个游戏对甲、乙两人公平，理由见解析.
【解析】
【分析】
（1）根据四个球中奇数的个数，除以总个数得到所求概率即可；
（2）列表得出所有等可能的情况数，找出两次摸出标号数字同为奇数或偶数的情况数，以及一奇一偶的情况数，分别求出两人获胜的概率，比较即可．
【详解】(1)∵标号分别为1，2，3，4的四个球中奇数为1，3，共2个， ∴P（摸到标号数字为奇数）= =
(2)列表如下：
所有等可能的情况数有16中，其中同为偶数或奇数的情况有：（1，1），（3，1），（2，2），（4，2），（1，3）（3，3），（2，4），（4，4），共8种情况；一奇一偶的情况有：（2，1），（4，1），（1，2），（3，2），（2，3），（4，3），（1，4），（3，4），共8种，
∴P（甲获胜）=P（乙获胜）= = ，
则这个游戏对甲、乙两人公平.
【点睛】此题考查了游戏公平性，以及列表法与树状图法，判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平．用到的知识点为：概率=所求情况数与总情况数之比．
22.如图，AB为⊙O的直径，AC、DC为弦，∠ACD=60°，P为AB延长线上的点，∠APD=30°．
（1）求证：DP是⊙O的切线；
（2）若⊙O的半径为3cm，求图中阴影部分的面积．
【答案】（1）证明见解析；（2）.
【解析】
【分析】
（1）连接OD，求出∠AOD，求出∠DOB，求出∠ODP，根据切线判定推出即可．
（2）求出OP、DP长，分别求出扇形DOB和△ODP面积，即可求出答案．
【详解】解：（1）证明：连接OD，
∵∠ACD=60°，
∴由圆周角定理得：∠AOD=2∠ACD=120°．
∴∠DOP=180°﹣120°=60°．
∵∠APD=30°，
∴∠ODP=180°﹣30°﹣60°=90°．
∴OD⊥DP．
∵OD为半径，
∴DP是⊙O切线．
（2）∵∠ODP=90°，∠P=30°，OD=3cm，
∴OP=6cm，由勾股定理得：DP=3cm．
∴图中阴影部分的面积
23.某公司今年1月份的生产成本是400万元，由于改进技术，生产成本逐月下降，3月份的生产成本是361万元．假设该公司2、3、4月每个月生产成本的下降率都相同．
（1）求每个月生产成本的下降率；
（2）请你预测4月份该公司的生产成本．
【答案】（1）每个月生产成本的下降率为5%；（2）预测4月份该公司的生产成本为342.95万元．
【解析】
【分析】
（1）设每个月生产成本的下降率为x，根据2月份、3月份的生产成本，即可得出关于x的一元二次方程，解之取其较小值即可得出结论；
（2）由4月份该公司的生产成本=3月份该公司的生产成本×（1﹣下降率），即可得出结论．
【详解】（1）设每个月生产成本的下降率为x，
根据题意得：400（1﹣x）2=361，
解得：x1=0.05=5%，x2=1.95（不合题意，舍去）．
答：每个月生产成本的下降率为5%；
（2）361×（1﹣5%）=342.95（万元），
答：预测4月份该公司的生产成本为342.95万元．
【点睛】本题考查了一元二次方程的应用，解题的关键是：（1）找准等量关系，正确列出一元二次方程；（2）根据数量关系，列式计算．
24.如图1，中，是的高.
（1）求证：.
（2）与相似吗？为什么？
（3）如图2，设的中点为的中点为，连接，求的长.
【答案】（1）见解析；（2），理由见解析；（3）
【解析】
【分析】
（1）由题意，BD、CE是高，则∠ADB＝∠AEC＝90°，是公共角，即可得出△ABD∽△ACE；
（2）由△ABD∽△ACE可推出，又 ，根据相似三角形的判定定理即可证得；
（3）连接、,根据等腰三角形的性质可得，，根据三角函数可得，进而可求得，由勾股定理即可求出FM的长.
【详解】（1）、是的高。
（2）
，即
（3）连接、,
∵BD是△ABC的高，M为BC的中点，
∴在Rt△CBD中，，
同理可得,
∴,
∵F是DE的中点，
∴,
由得
,
∴,
∵DE＝12,
∴，
∵，且,
∴.
【点睛】本题主要考查了相似三角形的判定和性质，直角三角形斜边上中线的性质以及等腰三角形的判定与性质.
25.某商店经销一种学生用双肩包，已知这种双肩包的成本价为每个30元．市场调查发现，这种双肩包每天的销售量y（个）与销售单价x（元）有如下关系：y=﹣x+60（30≤x≤60）．设这种双肩包每天的销售利润为w元．
（1）求w与x之间的函数关系式；
（2）这种双肩包销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？
（3）如果物价部门规定这种双肩包的销售单价不高于42元，该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为多少.
【答案】（1）w＝﹣x2+90x﹣1800；（2）当x＝45时，w有最大值，最大值是225；（3）该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为40元．
【解析】
【分析】
（1）每天的销售利润=每天的销售量×每件产品的利润；
（2）根据配方法，可得答案；
（3）根据自变量与函数值的对应关系，可得答案．
【详解】（1）w＝（x﹣30）•y
＝（﹣x+60）（x﹣30）
＝﹣x2+30x+60x﹣1800
＝﹣x2+90x﹣1800，
w与x之间的函数解析式w＝﹣x2+90x﹣1800；
（2）根据题意得：w＝﹣x2+90x﹣1800＝﹣（x﹣45）2+225，
∵﹣1＜0，
当x＝45时，w有最大值，最大值是225．
（3）当w＝200时，﹣x2+90x﹣1800＝200，
解得x1＝40，x2＝50，
∵50＞42，x2＝50不符合题意，舍，
答：该商店销售这种双肩包每天要获得200元的销售利润，销售单价应定为40元．
【点睛】本题考查的知识点是二次函数的应用，解题的关键是熟练的掌握二次函数的应用.
26.如图，是⊙的弦，交于点，过点的直线交的延长线于点，且是⊙的切线.
（1）判断的形状，并说明理由；
（2）若，求的长；
（3）设的面积是的面积是，且.若⊙的半径为，求.
【答案】（1）是等腰三角形，理由见解析；（2）的长为；（3）.
【解析】
【分析】
（1）首先连接OB，根据等腰三角形的性质由OA＝OB得,由点C在过点B的切线上，且，根据等角的余角相等，易证得∠PBC＝∠CPB，即可证得△CBP是等腰三角形；
（2）设BC＝x，则PC＝x，在Rt△OBC中，根据勾股定理得到，然后解方程即可；
（3）作CD⊥BP于D，由等腰三角形三线合一的性质得，由，通过证得，得出 即可求得CD，然后解直角三角形即可求得.
【详解】（1）是等腰三角形，理由：
连接，
⊙与相切与点，
，即，
，
是等腰三角形
（2）设，则，
在中，，，
，
，
解得，
即的长为；
（3）解：作于，
，
，，
，
，
，
，
，
.
【点睛】本题考查了切线的性质、勾股定理、等腰三角形的判定与性质以及三角形相似的判定和性质．此题难度适中，注意掌握辅助线的作法及数形结合思想的应用．
27.如图，抛物线交轴于、两点，交轴于点，点的坐标为，直线经过点、.
（1）求抛物线的函数表达式；
（2）点是直线上方抛物线上的一动点，求面积的最大值并求出此时点的坐标；
（3）过点的直线交直线于点，连接，当直线与直线的一个夹角等于的3倍时，请直接写出点的坐标.
【答案】（1）；（2），点坐标为；（3）点的坐标为，
【解析】
【分析】
（1）利用B（5，0）用待定系数法求抛物线解析式；
（2）作PQ∥y轴交BC于Q，根据求解即可；
（3）作∠CAN=∠NAM1=∠ACB，则∠A M1B=3∠ACB, 则 NAM1∽ A C M1,通过相似的性质来求点M1的坐标；作AD⊥BC于D,作M1关于AD的对称点M2, 则∠A M2C=3∠ACB,根据对称点坐标特点可求M2的坐标.
【详解】（1）把代入得
.
∴；
（2）作PQ∥y轴交BC于Q，设点，则

∵
∴OB=5，
∵Q在BC上，
∴Q的坐标为（x，x-5），
∴PQ==，
∴
=
=
∴当时，有最大值，最大值为，
∴点坐标为.
（3）如图1，作∠CAN=∠NAM1=∠ACB，则∠A M1B=3∠ACB,

∵∠CAN=∠NAM1,
∴AN=CN,
∵=-(x-1)(x-5),
∴A的坐标为（1，0），C的坐标为（0，-5），
设N的坐标为（a,a-5），则
∴，
∴a= ,
∴N的坐标为（,）,
∴AN2==，AC2=26，
∴，
∵∠NAM1=∠ACB，∠N M1A=∠C M1A，
∴ NAM1∽ A C M1,
∴,
∴
设M1的坐标为（b,b-5），则
∴,
∴b1= ，b2=6(不合题意，舍去)，
∴M1的坐标为，
如图2，作AD⊥BC于D,作M1关于AD的对称点M2, 则∠A M2C=3∠ACB,
易知ADB是等腰直角三角形，可得点D的坐标是（3，-2），
∴M2 横坐标= ，
M2 纵坐标= ，
∴M2 的坐标是，
综上所述，点M的坐标是或.
【点睛】本题考查了二次函数与几何图形的综合题：熟练掌握二次函数图象上点的坐标特征、二次函数的性质及相似三角形的判定与性质，会运用分类讨论的思想解决数学问题．选 手
甲
乙
丙
丁
平均数(环)
9.2
9.2
9.2
9.2
方差(环2)
0.035
0.015
0.025
0.027
1
2
3
4
1
（1，1）
（2，1）
（3，1）
（4，1）
2
（1，2）
（2，2）
（3，2）
（4，2）
3
（1，3）
（2，3）
（3，3）
（4，3）
4
（1，4）
（2，4）
（3，4）
（4，4）