2024年福建省泉州市名校数学九上开学综合测试试题【含答案】

这是一份2024年福建省泉州市名校数学九上开学综合测试试题【含答案】，共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）在某校举行的“我的中国梦”演讲比赛中，有5名学生参加决赛，他们决赛的最终成绩各不相同，其中的一名学生要想知道自己能否进入前3名，不仅要了解自己的成绩，还要了解这5名学生成绩的( )
A．众数B．方差C．中位数D．平均数
2、（4分）满足下列条件的四边形不是正方形的是（ ）
A．对角线相互垂直的矩形B．对角线相等的菱形
C．对角线相互垂直且相等的四边形D．对角线垂直且相等的平行四边形
3、（4分）如图顺次连接等腰梯形四边中点得到一个四边形，再顺次连接所得四边形四边的中点得到的图形是（ ）
A．等腰梯形B．直角梯形C．菱形D．矩形
4、（4分）如图，等边三角形的边长为4，点是△ABC的中心，，的两边与分别相交于，绕点顺时针旋转时，下列四个结论正确的个数是（ ）
①；②；③；④周长最小值是9.
A．1个B．2个C．3个D．4个
5、（4分）在Rt△ABC中，∠C＝90°．如果BC＝3，AC＝5，那么AB＝（ ）
A．B．4C．4或D．以上都不对
6、（4分）菱形的面积为2，其对角线分别为x、y，则y与x的图象大致（）．
A．B．
C．D．
7、（4分）甲车行驶40km与乙车行使30km所用的时间相同，已知甲车比乙车每小时多行驶15km．设甲车的速度为xkm/h，依题意，下列所列方程正确的是（ ）
A．＝B．＝C．＝D．＝
8、（4分）要使分式有意义，x应满足的条件是（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
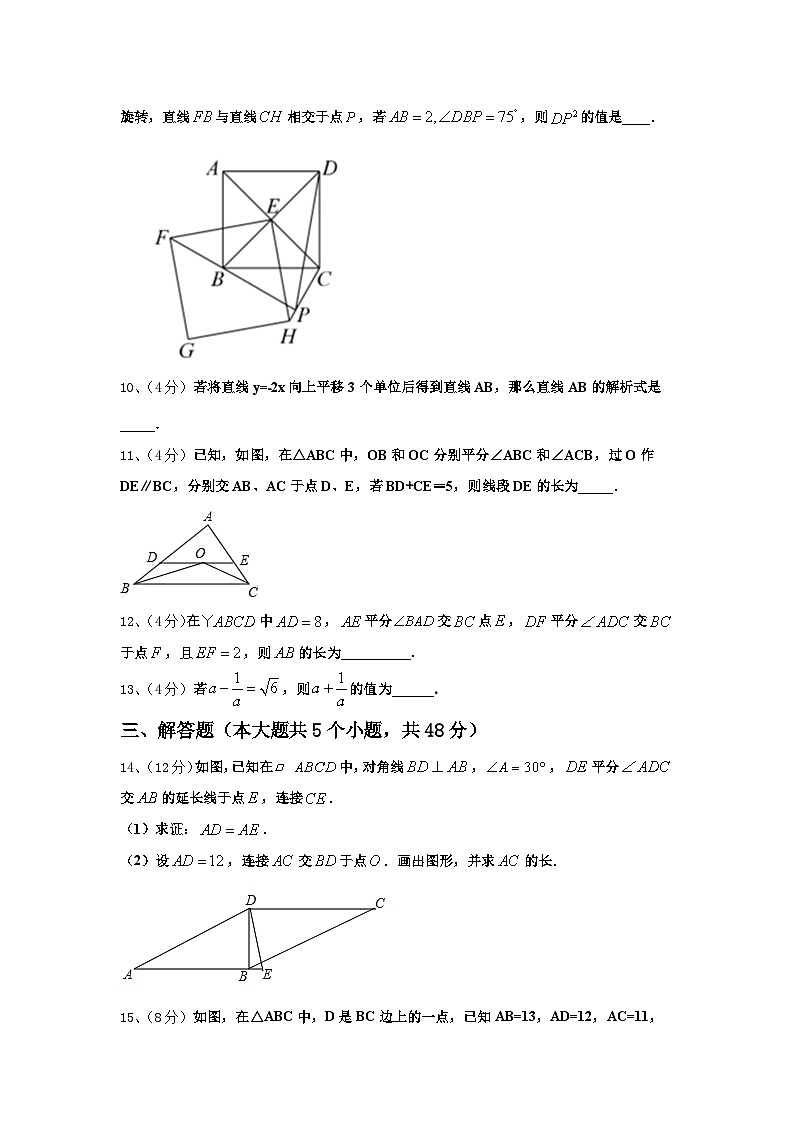
9、（4分）如图，正方形的对角线与相交于点，正方形绕点旋转，直线与直线相交于点，若，则的值是____．
10、（4分）若将直线y=﹣2x向上平移3个单位后得到直线AB，那么直线AB的解析式是_____．
11、（4分）已知，如图，在△ABC中，OB和OC分别平分∠ABC和∠ACB，过O作DE∥BC，分别交AB、AC于点D、E，若BD+CE＝5，则线段DE的长为_____．
12、（4分）在中，平分交点，平分交于点，且，则的长为__________.
13、（4分）若，则的值为______.
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，已知在中，对角线，，平分交的延长线于点，连接．
（1）求证：．
（2）设，连接交于点．画出图形，并求的长．
15、（8分）如图，在△ABC中，D是BC边上的一点，已知AB=13，AD=12，AC=11，BD=1．
(1)求证：AD⊥BC；
(2)求CD的长
16、（8分）甲、乙两校派相同人数的优秀学生，参加县教育局举办的中小学生美文诵读决赛。比赛结束后，发现学生成绩分别是7分、8分、9分或10分(满分10分)，核分员依据统计数据绘制了如下尚不完整的统计图表。根据这些材料，请你回答下列问题：
(1)在图①中，“7分”所在扇形的圆心角等于_______
(2)求图②中，“8分”的人数，并请你将该统计图补充完整。

(3)经计算，乙校学生成绩的平均数是8.3分，中位数是8分。请你计算甲校学生成绩的平均数、中位数，并从平均数和中位数的角度分析哪个学校的成绩较好？
(4)如果教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校？
17、（10分）如图，在平面直角坐标系中，已知直线，都经过点，它们分别与轴交于点和点，点、均在轴的正半轴上，点在点的上方．
（1）如果，求直线的表达式；
（2）在（1）的条件下，如果的面积为3，求直线的表达式．
18、（10分）地铁检票处有三个进站闸口A、B、C.
①人选择A进站闸口通过的概率是________；
②两个人选择不同进站闸口通过的概率.（用树状图或列表法求解）
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）既是矩形又是菱形四边形是________．
20、（4分）一个平行四边形的一条边长为3，两条对角线的长分别为4和，则它的面积为______.
21、（4分）计算： .
22、（4分）使式子的值为0，则a的值为_______.
23、（4分）如图，已知一次函数与y=2x+m的图象相交于，则关于的不等式的解集是__．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在中，为的中点，，.动点从点出发，沿方向以的速度向点运动；同时动点从点出发，沿方向以的速度向点运动，运动时间是秒.
（1）用含的代数式表示的长度.
（2）在运动过程中，是否存在某一时刻，使点位于线段的垂直平分线上？若存在，求出的值；若不存在，请说明理由.
（3）是否存在某一时刻，使？若存在，求出的值；若不存在，请说明理由.
（4）是否存在某一时刻，使？若存在，求出的值；若不存在，请说明理由.
25、（10分）如图，一次函数的图象与轴交于点A，正方形ABCD的顶点B在轴上，点D在直线上，且AO=OB，反比例函数（）经过点C．
（1）求一次函数和反比例函数的解析式；
（2）点P是轴上一动点，当的周长最小时，求出P点的坐标；
（3）在（2）的条件下，以点C、D、P为顶点作平行四边形，直接写出第四个顶点M的坐标．
26、（12分）如图，△ABC 的面积为 63，D 是 BC 上的一点，且 BD：BC＝2：3， DE∥AC 交 AB 于点 E，延长 DE 到 F，使 FE：ED＝2：1．连结 CF 交 AB 点于 G．
(1)求△BDE 的面积；
(2)求 的值；
(3)求△ACG 的面积．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
由于比赛取前3名进入决赛，共有5名选手参加，故应根据中位数的意义解答即可．
【详解】
解：因为5位进入决赛者的分数肯定是5名参赛选手中最高的，
而且5个不同的分数按从大到小排序后，中位数及中位数之前的共有3个数，
故只要知道自己的分数和中位数就可以知道是否进入决赛了；
故选：C．
此题主要考查统计的有关知识，主要包括平均数、中位数、众数、方差的意义．反映数据集中程度的统计量有平均数、中位数、众数、方差等，各有局限性，因此要对统计量进行合理的选择和恰当的运用．
2、C
【解析】
A.对角线相互垂直的矩形是正方形，故本项正确；B. 对角线相等的菱形是正方形，故本项正确；C.对角线互相垂直、平分、且相等的四边形才是正方形，故本项错误；D. 对角线垂直且相等的平行四边形是正方形，故本项正确.故选C.
3、D
【解析】
首先作出图形，根据三角形的中位线定理，可以得到，，，再根据等腰梯形的对角线相等，即可证得四边形EFGH的四边相等，即可证得是菱形，然后根据三角形中位线定理即可证得四边形OPMN的一组对边平行且相等，则是平行四边形，在根据菱形的对角线互相垂直，即可证得平行四边形的一组临边互相垂直，即可证得四边形OPMN是矩形．
【详解】
解：连接AC，BD．
∵E，F是AB，AD的中点，即EF是的中位线．
，
同理：，，．
又等腰梯形ABCD中，．
．
四边形EFGH是菱形．
是的中位线，
∴EF EG，，
同理，NMEG，
∴EFNM，
四边形OPMN是平行四边形．
，，
又菱形EFGH中，，
平行四边形OPMN是矩形．
故选：D．
本题考查了等腰梯形的性质，菱形的判定，矩形的判定，以及三角形的中位线定理，关键的应用三角形的中位线定理得到四边形EFGH和四边形OPMN的边的关系．
4、B
【解析】
首先连接OB、OC，如图，利用等边三角形的性质得∠ABO=∠OBC=∠OCB=30°，再证明∠BOD=∠COE，于是可判断△BOD≌△COE，利用全等三角形的对应边相等可对①进行判断；再利用S =S 得到四边形ODBE的面积= S ，则可对③进行判断，然后作OH⊥DE，则DH=EH，计算出S = OE，利用S△ODE随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断，
接下来由△BDE的周长=BC+DE=4+DE=4+OE，结合垂线段最短，当OE⊥BC时，OE最小，△BDE的周长最小，计算出此时OE的长则可对④进行判断.
【详解】
连接OB，OC，如图.
∵△ABC为等边三角形，
∴∠ABC=∠ACB=60°.
∵点O是△ABC的中心，
∴OB=OC，OB. OC分别平分∠ABC和∠ACB，
∴∠ABO=∠OBC=∠OCB=30°，
∴∠BOC=120°，即∠BOE+∠COE=120°，
而∠DOE=120°，即∠BOE+∠BOD=120°，
∴∠BOD=∠COE.
在△BOD和△COE中，∠BOD=∠COE，BO=CO，∠OBD=∠OCE，
∴△BOD≌△COE，
∴BD=CE，OD=OE，所以①正确；
∴S =S ，
∴四边形ODBE的面积=S = S =× ×4 = ，所以③正确；
作OH⊥DE，如图，则DH=EH，
∵∠DOE=120°，
∴∠ODE=∠OEH=30°．
∴OH=OE，HE=OH= OE，
∴DE= OE，
∴S△ODE= ··OE· OE= OE，
即S 随OE的变化而变化，而四边形ODBE的面积为定值，
∴S≠S ，所以②错误；
∵BD=CE，
∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=4+DE=4+ OE，
当OE⊥BC时，OE最小，△BDE的周长最小，此时OE= ，
∴△BDE周长的最小值=4+2=6，所以④错误.
故选B.
此题考查旋转的性质、等边三角形的性质和全等三角形的判定与性质，解题关键是牢记旋转前、后的图形全等.
5、A
【解析】
解：∵∠C=90°，AC=5，BC=3，∴AB===．故选A．
6、C
【解析】
先根据菱形的面积公式，得出x、y的函数关系，再根据x的取值范围选出答案．
【详解】
∵菱形的面积S=
∴，即y=
其中，x＞0
故选：C
本题考查菱形面积公式的应用，注意在求解出x、y的关系后，还需要判断x的取值范围．
7、A
【解析】
设甲车的速度为xkm/h，则乙车的速度为（x-15）km/h，根据时间=路程÷速度结合甲车行驶40km与乙车行使30km所用的时间相同，即可得出关于x的分式方程，此题得解．
【详解】
设甲车的速度为xkm/h，则乙车的速度为（x﹣15）km/h，
根据题意得：＝．
故选A．
本题考查了由实际问题抽象出分式方程，找准等量关系，正确列出分式方程是解题的关键．
8、D
【解析】
直接利用分式有意义的条件，即分母不等于0，进而得出答案．
【详解】
解：要使分式有意义，x应满足的条件是：x-1≠0，
解得：x≠1．
故选：D．
本题考查分式有意义的条件，正确把握分式有意义的条件是解题关键．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
如图，设EF交AB于M，EH交BC于N，PF交EH于O，作PT⊥AD于T交BC于R．首先证明∠CPB＝90°，求出DT，PT即可解决问题．
【详解】
解：如图，设EF交AB于M，EH交BC于N，PF交EH于O，作PT⊥AD于T交BC于R．
∵四边形ABCD是正方形，
∴AC⊥BD，AE＝EB，∠EAM＝∠EBN＝45°，
∵四边形EFGH是正方形，
∴∠MEN＝∠AEB＝90°，
∴∠AEM＝∠BEN，
∴△AEM≌△BEN（ASA），
∴AM＝BN，EM＝EN，∠AME＝∠BNE，
∵AB＝BC，EF＝EH，
∴FM＝NH，BM＝CN，
∵∠FMB＝∠AME，∠CNH＝∠BNE，
∴∠FMB＝∠CNH，
∴△FMB≌△HNC（SAS），
∴∠MFB＝∠NHC，
∵∠EFO＋∠EOF＝90°，∠EOF＝∠POH，
∴∠POH＋∠PHO＝90°，
∴∠OPH＝∠BPC＝90°，
∵∠DBP＝75°，∠DBC＝45°，
∴∠CBP＝30°，
∵BC＝AB＝2，
∴PB＝BC•cs30°＝，PR＝PB＝，RC＝PR•tan30°＝，
∵∠RTD＝∠TDC＝∠DCR＝90°，
∴四边形TDCR是矩形，
∴TD＝CR＝，TR＝CD＝AB＝2，
在Rt△PDT中，PD2＝DT2＋PT2＝，
故答案为.
本题考查全等三角形的判定和性质，旋转变换，正方形的性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．
10、y=﹣2x+1．
【解析】
利用直线的平移规律：（1）k不变；（2） “上加下减，左加右减”的原则进行解答即可．
【详解】
∵将直线y=﹣2x向上平移1个单位，
∴y=﹣2x+1，
即直线的AB的解析式是y=﹣2x+1.
故答案为：y=﹣2x+1．
本题考查了一次函数图象平移的特点.熟练应用一次函数平移规律是解题的关键.
11、1
【解析】
根据OB和OC分别平分∠ABC和∠ACB，和DE∥BC，利用两直线平行，内错角相等和等量代换，求证出DB=DO，OE=EC．然后即可得出答案．
【详解】
解：∵在△ABC中，OB和OC分别平分∠ABC和∠ACB，
∴∠DBO=∠OBC，∠ECO=∠OCB，
∵DE∥BC，
∴∠DOB=∠OBC=∠DBO，∠EOC=∠OCB=∠ECO，
∴DB=DO，OE=EC，
∵DE=DO+OE，
∴DE=BD+CE=1．
故答案为1．
此题主要考查学生对等腰三角形的判定与性质平行线段性质的理解和掌握，此题关键是求证DB=DO，OE=EC，难度不大，是一道基础题．
12、或
【解析】
根据平行线的性质得到∠ADF＝∠DFC，由DF平分∠ADC，得到∠ADF＝∠CDF，等量代换得到∠DFC＝∠FDC，根据等腰三角形的判定得到CF＝CD，同理BE＝AB，根据已知条件得到四边形ABCD是平行四边形，根据平行四边形的性质得到AB＝CD，AD＝BC，即可得到结论．
【详解】
解：①如图1，在▱ABCD中，∵BC＝AD＝8，BC∥AD，CD＝AB，CD∥AB，
∴∠DAE＝∠AEB，∠ADF＝∠DFC，
∵AE平分∠BAD交BC于点E，DF平分∠ADC交BC于点F，
∴∠BAE＝∠DAE，∠ADF＝∠CDF，
∴∠BAE＝∠AEB，∠CFD＝∠CDF，
∴AB＝BE，CF＝CD，
∵EF＝2，
∴BC＝BE＋CF−EF＝2AB−EF＝8，
∴AB＝1；
②在▱ABCD中，∵BC＝AD＝8，BC∥AD，CD＝AB，CD∥AB，
∴∠DAE＝∠AEB，∠ADF＝∠DFC，
∵AE平分∠BAD交BC于点E，DF平分∠ADC交BC于点F，
∴∠BAE＝∠DAE，∠ADF＝∠CDF，
∴∠BAE＝∠AEB，∠CFD＝∠CDF，
∴AB＝BE，CF＝CD，
∵EF＝2，
∴BC＝BE＋CF＝2AB＋EF＝8，
∴AB＝3；
综上所述：AB的长为3或1．
故答案为：3或1.
本题考查了等腰三角形的判定和性质，平行线的性质，平行四边形的性质，解答本题的关键是判断出AB＝BE，CF＝CD．
13、.
【解析】
由可得，化简即可得到，再计算，即可求得=.
【详解】
∵，
∴，
∴，
∴，
∴=.
故答案为：.
本题考查了完全平方公式的变形应用，正确求得是解决问题的关键.
三、解答题（本大题共5个小题，共48分）
14、（1）证明见解析；（2）．
【解析】
（1）根据角平分线的性质可得∠ADE＝∠CDE，再根据平行四边形的性质和平行线的性质可得∠CDE＝∠AED，利用等量代换可得∠ADE＝∠AED，根据等角对等边可得AD＝AE；
（2）首先利用直角三角形的性质计算出BD，根据勾股定理可得AB长，然后再根据平行四边形的性质得出，，再利用勾股定理可得OA的值，进而可得答案．
【详解】
（1）证明：∵DE平分∠ADC，
∴∠ADE＝∠CDE，
∵四边形ABCD是平行四边形，
∴CD∥AB，
∴∠CDE＝∠AED，
∴∠ADE＝∠AED，
∴AD＝AE；
（2）解：在中，∠DAB＝30°，AD＝12，
∴，
∴，
∵四边形ABCD是平行四边形，
∴，，
在中，，
∴．
本题主要考查了平行四边形的性质，直角三角形的性质，角平分线的性质以及勾股定理的应用，解题的关键是掌握平行四边形的对角线互相平分．
15、9
【解析】
（1）逆用勾股定理即可正确作答.
（2）在RT△ADC，应用勾股定理即可求解.
【详解】
(1)证明：∵122=144，12=21，132=169
∴12+122=132
即BD2+AD2=AB2
∴△ABD是直角三角形
∴∠ADB=90°
∴AD⊥BC
(2)解：∵AD⊥BC
∴∠ADC=90°
在RT△ADC中
CD2=AC2-AD2
CD=
CD=9
∴CD的长为9
本题主要考查了勾股定理及其逆定理的应用。灵活应用勾股定理是解决一些实际问题的关键.
16、（1）144°；（2）3人，补图见解析；（3）8.3分，7分，乙校；（4）甲校．
【解析】
分析：（1）利用360°减去其它各组对应的圆心角即可求解；
（2）首先求得乙校参赛的人数，即可求得成绩是8分的人数，从而将条形统计图补充完整；
（3）首先求得得分是9分的人数，然后根据平均数公式和中位数的定义求解；
（4）只要比较每个学校前8名的成绩即可．
详解：（1）“7分”所在扇形的圆心角等于360°-90°-72°-54°=144°；
（2）乙校参赛的总人数是：4÷=20（人），
则成绩是8分的人数是：20-8-4-5=3（人）．
；
（3）甲校中得分是9分的人数是：20-11-8=1（人）．
则甲校的平均分是：=8.3（分），
甲校的中位数是：7分；
两校的平均数相同，但乙校的中位数大于甲校的中位数，说明乙校的成绩高于甲校的成绩.
（4）甲得分是10分的正好有8人，而乙班得分是10分的有5人，不足8人，则应选择甲校．
点睛：本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．
17、（1）；（2）．
【解析】
（1）先根据A点坐标求出OA的长度，然后根据求出OB的长度，进而得到B点的坐标，最后利用待定系数法即可求出直线的表达式；
（2）首先利用的面积求出点C的坐标，然后利用待定系数法即可求出直线的表达式．
【详解】
（1），
．
，
点在轴正半轴，
．
设的函数解析式为，
把，代入得
解得：，
．
（2），
，
∵，
．
设，则，
点在点上方，
，
．
设的函数解析式为，
把，代入得，
解得：，
．
本题主要考查一次函数，掌握待定系数法及数形结合是解题的关键．
18、（1）；（2）
【解析】
（1）直接利用概率公式计算可得；
（2）画树状图展示所有9种等可能的结果数，再找出选择不同通道通过的结果数，然后根据概率公式求解．
【详解】
解：（1）选择A通道通过的概率是；
故答案为：
（2）画树形图如下；
由图中可知，共有9种等可能情况，其中选择不同通道通过的有6种结果，
所以选择不同通道通过的概率为
本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式求事件A或B的概率．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、正方形
【解析】
根据正方形的判定定理即可得到结论．
【详解】
既是矩形又是菱形的四边形是正方形，
故答案为正方形．
本题考查了正方形的判定，熟练掌握正方形的判定定理是解题的关键．
20、4
【解析】
如图所示：
∵四边形ABCD是平行四边形

∵

即两条对角线互相垂直，
∴这个四边形是菱形，
∴
故答案为
21、1.
【解析】
解：.
故答案为1
22、
【解析】
根据分式值为0，分子为0，分母不为0解答即可.
【详解】
∵的值为0，
∴2a-1=0，a+2≠0，
∴a=.
故答案为：
本题考查分式为0的条件，要使分式值为0，则分子为0，分母不为0；熟练掌握分式为0的条件是解题关键.
23、x>-1
【解析】
观察图象，找出直线y=-x+2在直线y=2x+m的下方时对应的x的取值范围即可.
【详解】
从图象可以看出，当时，直线y=-x+2在直线y=2x+m的下方，
所以的解集为：x>-1，
故答案为：．
本题考查了一次函数与一元一次不等式，体现了数形结合的思想方法，准确的确定出的值是解答本题的关键．
二、解答题（本大题共3个小题，共30分）
24、 (1)CP=8-3t;(2)见解析;(3)见解析;(4)见解析.
【解析】
（1）直接利用即可求解；
（2）根据线段垂直平分线的性质可得，列方程求解即可；
（3）根据全等三角形的性质可得若，因为，，所以只需，列方程求出的值即可；
（4）若，因为，所以需满足且，即且，没有符合条件的t的值，故不存在.
【详解】
解：（1）；
（2）若点位于线段的垂直平分线上，
则，
即，
解得.
所以存在，秒时点位于线段的垂直平分线上.
（3）若，
因为，，
所以只需，
即，解得，
所以存在.
（4）若，
因为，
所以需满足且，
即且，
所以不存在.
本题考查全等三角形的判定和性质及动点运动问题，对于运动型的问题，关键是用时间t表示出相应的线段的长度，能根据题意列方程求解．
25、（1）y=x+1，；（1）P（，0）；（3）M的坐标为（，1），（，6）或（，﹣1）．
【解析】
（1）设一次函数y=kx+1的图象与x轴交于点E，连接BD，利用一次函数图象上点的坐标特征、正方形的性质以及等腰三角形的性质可得出点E的坐标，由点E的坐标利用待定系数法可求出一次函数解析式，由BD∥OA，OE=OB可求出BD的长，进而可得出点D的坐标，由正方形的性质可求出点C的坐标，再利用反比例函数图象上点的坐标特征可求出反比例函数解析式；
（1）作点D关于x轴的对称点D'，连接CD'交x轴于点P，此时△PCD的周长取最小值，由点D的坐标可得出点D'的坐标，由点C，D'的坐标，利用待定系数法可求出直线CD'的解析式，再利用一次函数图象上点的坐标特征可求出点P的坐标；
（3）设点M的坐标为（x，y），分DP为对角线、CD为对角线及CP为对角线三种情况，利用平行四边形的性质（对角线互相平分）可求出点M的坐标，此题得解．
【详解】
（1）设一次函数y=kx+1的图象与x轴交于点E，连接BD，如图1所示．
当x=0时，y=kx+1=1，∴OA=1．
∵四边形ABCD为正方形，OA=OB，∴∠BAE=90°，∠OAB=∠OBA=45°，∴∠OAE=∠OEA=45°，∴OE=OA=1，点E的坐标为（﹣1，0）．
将E（﹣1，0）代入y=kx+1，得：﹣1k+1=0，解得：k=1，∴一次函数的解析式为y=x+1．
∵∠OBD=∠ABD+∠OBA=90°，∴BD∥OA．
∵OE=OB=1，∴BD=1OA=4，∴点D的坐标为（1，4）．
∵四边形ABCD为正方形，∴点C的坐标为（1+1﹣0，0+4﹣1），即（4，1）．
∵反比例函数y（x＞0）经过点C，∴n=4×1=8，∴反比例函数解析式为y．
（1）作点D关于x轴的对称点D'，连接CD'交x轴于点P，此时△PCD的周长取最小值，如图1所示．
∵点D的坐标为（1，4），∴点D'的坐标为（1，﹣4）．
设直线CD'的解析式为y=ax+b（a≠0），将C（4，1），D'（1，﹣4）代入y=ax+b，得：，解得：，∴直线CD'的解析式为y=3x﹣2．
当y=0时，3x﹣2=0，解得：x，∴当△PCD的周长最小时，P点的坐标为（，0）．
（3）设点M的坐标为（x，y），分三种情况考虑，如图3所示．
①当DP为对角线时，，解得：，∴点M1的坐标为（，1）；
②当CD为对角线时，，解得：，∴点M1的坐标为（，6）；
③当CP为对角线时，，解得：，∴点M3的坐标为（，﹣1）．
综上所述：以点C、D、P为顶点作平行四边形，第四个顶点M的坐标为（，1），（，6）或（，﹣1）．
本题考查了待定系数法求一次函数解析式、反比例函数图象上点的坐标特征、正方形的性质、等腰三角形的性质、三角形中位线、反比例函数图象上点的坐标特征、一次函数图象上点的坐标特征以及平行四边形的性质，解题的关键是：（1）利用等腰三角形的性质及正方形的性质，求出点E，C的坐标；（1）利用两点之间线段最短，确定点P的位置；（3）分DP为对角线、CD为对角线及CP为对角线三种情况，利用平行四边形的对角线互相平分求出点M的坐标．
26、（1）△BDE的面积是28；（2）；（3）9
【解析】
（1）因为DE∥AC，所以△BDE∽△BCA，由相似三角形的性质：面积比等于相似比的平方可得到△BDE的面积；
（2）若要求 的值，可由相似三角形的性质分别得到AC和DE的数量关系、EF和DE的数量关系即可；
（3）由（1）可知△BDE的面积是28，因为BD：BC=2：3，所以BD：CD=2：1，又因为三角形BDE和三角形CDE中BD和CD边上的高相等，所以S =14，进而求出四边形ACDE的面积是35和S =21，利用相似三角
【详解】
(1)∵DE∥AC，
∴△BDE∽△BCA，
∴ ，
∵BD:BC=2:3，
∴ ，
∵△ABC的面积为63，
∴△BDE的面积是28；
(2)∵DE∥AC，
∴ ,
∴AC= ED，
∵FE:ED=2:1，
∴EF=2ED，
∴ ；
(3)∵△BDE的面积是28，
∴S =14，
∴四边形ACDE的面积是35，
∴S =21，
∵DE∥AC，
∴△GEF∽△GAC，
∴ ，
∴S = ×21=9.
此题考查相似三角形的判定与性质，三角形的面积，解题关键在于得到△BDE∽△BCA
题号
一
二
三
四
五
总分
得分
批阅人
甲校成绩统计表
成绩
7分
8分
9分
10分
人数
11
0
8