2024年福建省厦门外国语学校数学九上开学统考模拟试题【含答案】

这是一份2024年福建省厦门外国语学校数学九上开学统考模拟试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）已知，则下列结论正确的是( )
A．B．C．D．
2、（4分）如图，将ABC绕点A顺时针旋转70°后，得到ADE，下列说法正确的是（ ）
A．点B的对应点是点EB．∠CAD=70°C．AB=DED．∠B=∠D
3、（4分）如图，点O在ABC内，且到三边的距离相等，若∠A=60°，则∠BOC的大小为( )
A．135°B．120°C．90°D．60°
4、（4分）已知m、n是正整数，若+是整数，则满足条件的有序数对（m，n）为（ ）
A．（2，5）B．（8，20）C．（2，5），（8，20）D．以上都不是
5、（4分）如图，正比例函数和一次函数的图像相交于点.当时，则（ ）
A．B．C．D．
6、（4分）下列交通标志中、既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
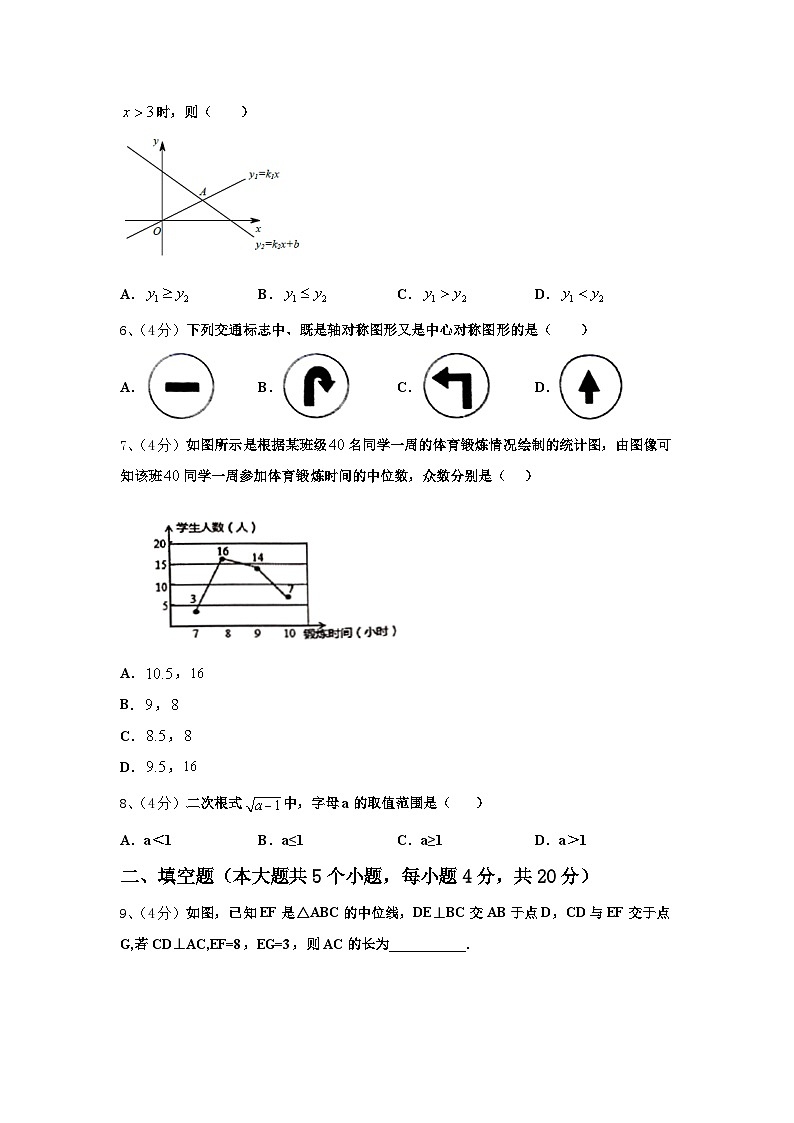
7、（4分）如图所示是根据某班级名同学一周的体育锻炼情况绘制的统计图，由图像可知该班同学一周参加体育锻炼时间的中位数，众数分别是（ ）
A．，
B．，
C．，
D．，
8、（4分）二次根式中，字母a的取值范围是（ ）
A．a＜1B．a≤1C．a≥1D．a＞1
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图，已知EF是△ABC的中位线，DE⊥BC交AB于点D，CD与EF交于点G,若CD⊥AC,EF=8，EG=3，则AC的长为___________.
10、（4分）如图，在平面直角坐标系中，已知，，是轴上的一条动线段，且，当取最小值时，点坐标为______.
11、（4分）不改变分式的值，使分子、分母的第一项系数都是正数，则＝_____．
12、（4分）如图，在中，，点、、分别为、、的中点，若，则_________.
13、（4分）直角三角形的一条直角边长是另一条直角边长的2倍,斜边长是10,则较短的直角边的长为___________.
三、解答题（本大题共5个小题，共48分）
14、（12分）（1）探究新知：如图1，已知△ABC与△ABD的面积相等，试判断AB与CD的位置关系，并说明理由．
（2）结论应用：① 如图2，点M，N在反比例函数（k＞0）的图象上，过点M作ME⊥y轴，过点N作NF⊥x轴，垂足分别为E，F．试证明：MN∥EF．
② 若①中的其他条件不变，只改变点M，N的位置如图3所示，请判断 MN与EF是否平行？请说明理由.
15、（8分）如图，□ABCD中，在对角线BD上取E、F两点，使BE＝DF，连AE，CF，过点E作EN⊥FC交FC于点N，过点F作FM⊥AE交AE于点M；
（1）求证：△ABE≌△CDF；
（2）判断四边形ENFM的形状，并说明理由．
16、（8分）为了预防流感，某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中，室内每立方米空气中的含药量y（mg）与时间t（h）成正比；药物释放完毕后，y与t之间的函数解析式为y=（a为常数），如图所示. 根据图中提供的信息，解答下列问题：
（1）写出从释放药物开始，y与t之间的两个函数解析式及相应的自变量取值范围；
（2）据测定，当空气中每立方米的含药量降低到0.25mg以下时，学生方可进入教室，那么药物释放开始，至少需要经过多少小时，学生才能进入教室？
17、（10分）某超市预测某饮料会畅销、先用1800元购进一批这种饮料，面市后果然供不应求，又用8100元购进这种饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贵2元．
（1）第一批饮料进货单价多少元？
（2）若两次进饮料都按同一价格销售，两批全部售完后，获利不少于2700元，那么销售单价至少为多少元？
18、（10分）如图，在△ABC中，，，，求AB的长．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）如图，在△ABC中，∠C＝90°，AD平分∠CAB，BC＝6，BD＝4，则点D到AB的距离是_________．
20、（4分）如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是__________．
21、（4分）已知，则________
22、（4分）如图，点G为正方形ABCD内一点，AB＝AG，∠AGB＝70°，联结DG，那么∠BGD＝_____度．
23、（4分）本市5月份某一周毎天的最高气温统计如下表：则这组数据的众数是___．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图，在△ABC中，BD、CE分别为AC、AB边上的中线，BD、CE交于点H，点G、F分别为HC、HB的中点，连接AH、DE、EF、FG、GD，其中HA＝BC．
（1）证明：四边形DEFG为菱形；
（2）猜想当AC、AB满足怎样的数量关系时，四边形DEFG为正方形，并说明理由．
25、（10分）如图,某同学想测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米,在同一时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上的影长为21米,落在墙上的影高为6米,求旗杆的高度.

26、（12分）如图1，在平面直角坐标系中，直线AB经过点C（a，a），且交x轴于点A（m，1），交y轴于点B（1，n），且m，n满足＋（n﹣12）2＝1．
（1）求直线AB的解析式及C点坐标；
（2）过点C作CD⊥AB交x轴于点D，请在图1中画出图形，并求D点的坐标；
（3）如图2，点E（1，﹣2），点P为射线AB上一点，且∠CEP＝45°，求点P的坐标．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
根据不等式的性质，求出不等式的解集即可．
【详解】
解：不等式两边都除以2，
得：，
故选：D．
本题考查了解一元一次不等式，能根据题意得出不等式的解集是解此题的关键．
2、D
【解析】
根据旋转的性质逐项判断即得答案．
【详解】
解：因为将△ABC绕点A顺时针旋转70°后，得到△ADE，所以：
A、点B的对应点是点D，不是点E，故本选项说法错误，不符合题意；
B、∠CAD不是旋转角，不等于70°，故本选项说法错误，不符合题意；
C、AB=AD≠DE，故本选项说法错误，不符合题意；
D、∠B=∠D，故本选项说法正确，符合题意．
故选：D．
本题考查了旋转的性质，属于基础题型，熟练掌握旋转的性质是关键．
3、B
【解析】
由条件可知O为三角形三个内角的角平分线的交点，则可知∠OBC+∠OCB=（∠ABC+∠ACB）=（180°-∠A），在△BOC中利用三角形的内角和定理可求得∠BOC．
【详解】
∵O到三边的距离相等
∴BO平分∠ABC，CO平分∠ACB
∴∠OBC+∠OCB=(∠ABC+∠ACB)=(180°−∠A)
∵∠A=60°
∴∠OBC+∠OCB=60°
∴∠BOC=180°−(∠OBC+∠OCB)=180°−60°=120°
故选B.
本题考查了角平分线的性质，熟练掌握角平分线把一个角分成两个相等的角是解题的关键．
4、C
【解析】
根据二次根式的性质分析即可得出答案．
【详解】
解：∵+是整数，m、n是正整数，
∴m=2，n=5或m=8，n=20，
当m=2，n=5时，原式=2是整数；
当m=8，n=20时，原式=1是整数；
即满足条件的有序数对（m，n）为（2，5）或（8，20），
故选：C．
本题考查了二次根式的性质和二次根式的运算，估算无理数的大小的应用，题目比较好，有一定的难度．
5、C
【解析】
由图象可以知道，当x=3时，两个函数的函数值是相等的，再根据函数的增减性即可得到结论.
【详解】
解：由图象知，当x＞3时，y1的图象在y2上方，
y2故答案为：D.
本题考查了两条直线相交与平行，正确的识别图象是解题的关键.
6、A
【解析】
根据中心对称图形和轴对称图形的概念对各选项分析判断即可得解．
【详解】
A、既是轴对称图形又是中心对称图形，故本选项正确；
B、不是轴对称图形，也不是中心对称图形，故本选项错误；
C、不是轴对称图形，也不是中心对称图形，故本选项错误；
D、是轴对称图形，不是中心对称图形，故本选项错误．
故选：A．
本题考查了轴对称图形和中心对称图形的识别，熟练掌握轴对称图形和中心对称图形的定义是解答本题的关键. 在平面内，一个图形经过中心对称能与原来的图形重合，这个图形叫做叫做中心对称图形；一个图形的一部分，以某条直线为对称轴，经过轴对称能与图形的另一部分重合，这样的图形叫做轴对称图形.
7、B
【解析】
根据中位数、众数的概念分别求解即可．
【详解】
将这组数据从小到大的顺序排列后，处于中间位置的那个数，由中位数的定义可知，这组数据的中位数是9；
众数是一组数据中出现次数最多的数，即8；
故选：B
考查了中位数、众数的概念，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），叫做这组数据的中位数，如果中位数的概念掌握得不好，不把数据按要求重新排列，就会错误地将这组数据最中间的那个数当作中位数．
8、C
【解析】
由二次根式有意义的条件可知a-1≥0，解不等式即可.
【详解】
由题意a-1≥0
解得a≥1
故选C.
本题考查了二次根式的意义，掌握被开方数需大于等于0即可解题.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1
【解析】
由三角形中位线定理得出AB=2EF=16，EF∥AB，AF=CF，CE=BE，证出GE是△BCD的中位线，得出BD=2EG=6，AD=AB-BD=10，由线段垂直平分线的性质得出CD=BD=6，再由勾股定理即可求出AC的长．
【详解】
∵EF是△ABC的中位线，
∴AB=2EF=16，EF∥AB，AF=CF，CE=BE，
∴G是CD的中点，
∴GE是△BCD的中位线，
∴BD=2EG=6，
∴AD=AB-BD=10，
∵DE⊥BC，CE=BE，
∴CD=BD=6，
∵CD⊥AC，
∴∠ACD=90°，
∴AC=；
故答案为：1．
本题考查了三角形中位线定理、线段垂直平分线的性质、勾股定理等知识；熟练掌握三角形中位线定理，求出CD=BD是解题的关键．
10、
【解析】
如图把点A向右平移1个单位得到E（1，1），作点E关于x轴的对称点F（1，-1），连接BF，BF与x轴的交点即为点Q，此时AP+PQ+QB的值最小，求出直线BF的解析式，即可解决问题．
【详解】
解：如图把点4向右平移1个单位得到E（1，1），作点E关于x轴的对称点F（1，-1），连接BF，BF与x轴的交点即为点Q，此时4P+PQ+QB的值最小.
设最小BF的解析式为y=kx+b，则有解得
∴直线BF的解析式为y=x-2，
令y=0，得到x=2.
∴Q（2.0）
故答案为（2，0）.
本题考查轴对称最短问题、坐标与图形的性质、一次函数的应用等知识，解题的关键是学会利用对称解决最短问题，学会构建一次函数解决交点问题，属于中考常考题型
11、
【解析】
根据分式的基本性质即可求出答案．
【详解】
原式＝＝，
故答案为：
本题考查分式的基本性质，分式的基本性质是分式的分子和分母同时乘以或除以同一个不为0的整式，分式的值不变；熟练掌握分式的基本性质是解题关键．
12、1
【解析】
根据直角三角形的性质求出AB，根据三角形中位线定理求出EF．
【详解】
解：∵∠ACB＝90°，点D为AB的中点，
∴AB＝2CD＝16，
∵点E、F分别为AC、BC的中点，
∴EF＝AB＝1，
故答案为：1．
本题考查的是三角形中位线定理、直角三角形的性质，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．
13、1
【解析】
根据边之间的关系，运用勾股定理，列方程解答即可．
【详解】
由题意可设两条直角边长分别为x，2x，
由勾股定理得x2+(2x)2=(1)2，
解得x1=1，x2=-1舍去），
所以较短的直角边长为1．
故答案为：1
本题考查了一元二次方程和勾股定理的应用，解题的关键是根据勾股定理得到方程，转化为方程问题．
三、解答题（本大题共5个小题，共48分）
14、（1）AB∥CD．理由见解析；（1）①证明见解析；②MN∥EF．理由见解析.
【解析】
（1）分别过点C，D，作CG⊥AB，DH⊥AB，然后证明四边形CGHD为平行四边形后可得AB∥CD；（1）①连结MF，NE． 设点M的坐标为（x1，y1），点N的坐标为（x1，y1）．利用反比例函数的性质结合条件得出S△EFM＝S△EFN．可得MN∥EF．（3）MN∥EF． 证明与①类似.
【详解】
解：（1）分别过点C，D，作CG⊥AB，DH⊥AB，垂足为G，H，
则∠CGA＝∠DHB＝90°．
∴CG∥DH．
∵△ABC与△ABD的面积相等，
∴CG＝DH．
∴ 四边形CGHD为平行四边形．
∴AB∥CD．
（1）①连结MF，NE．
设点M的坐标为（x1，y1），点N的坐标为（x1，y1）．
∵ 点M，N在反比例函数（k＞0）的图象上，
∴，
∵ME⊥y轴，NF⊥x轴
∴OE＝y1，OF＝x1．
∴S△EFM＝
S△EFN＝．
∴S△EFM＝S△EFN．
由（1）中的结论可知：MN∥EF．
② MN∥EF． 证明与①类似，略．
本题考查1.平行四边形的判定与性质1.反比例函数的性质，综合性较强.
15、（1）见解析；（2）四边形ENFM是矩形．见解析.
【解析】
（1）根据SAS即可证明；
（2）只要证明三个角是直角即可解决问题；
【详解】
（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AB＝CD
∴∠ABD＝∠CDB，又∵BE＝DF，
∴△ABE≌△CDF（SAS）．
（2）由（1）得，∴∠AEB＝∠CFD，
∴∠AED＝∠CFB，
∴AE∥CF
又∵EN⊥CF，∠AEN＝∠ENF＝90°，
又∵FM⊥AE，∠FME＝90°，
∴四边形ENFM是矩形．
本题考查平行四边形的性质、全等三角形的判定和性质、矩形的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
16、 (1)y＝t（0≤t≤） (2)6小时
【解析】
(1) 将点代入函数关系式, 解得, 有
将代入, 得, 所以所求反比例函数关系式为;
再将代入, 得,所以所求正比例函数关系式为.
(2) 解不等式, 解得,
所以至少需要经过6小时后，学生才能进入教室.
17、 (1)4元/瓶．(2) 销售单价至少为1元/瓶．
【解析】
（1）设第一批饮料进货单价为x元/瓶，则第二批饮料进货单价为（x+2）元/瓶，根据数量＝总价÷单价结合第二批购进饮料的数量是第一批的3倍，即可得出关于x的分式方程，解之经检验后即可得出结论；
（2）由数量＝总价÷单价可得出第一、二批购进饮料的数量，设销售单价为y元/瓶，根据利润＝销售单价×销售数量﹣进货总价结合获利不少于2100元，即可得出关于y的一元一次不等式，解之取其最小值即可得出结论．
【详解】
（1）设第一批饮料进货单价为x元/瓶，则第二批饮料进货单价为（x+2）元/瓶，
依题意，得：＝3×，
解得：x＝4，
经检验，x＝4是原方程的解，且符合题意．
答：第一批饮料进货单价是4元/瓶；
（2）由（1）可知：第一批购进该种饮料450瓶，第二批购进该种饮料1350瓶．
设销售单价为y元/瓶，
依题意，得：（450+1350）y﹣1800﹣8100≥2100，
解得：y≥1．
答：销售单价至少为1元/瓶．
本题考查了分式方程的应用以及一元一次不等式的应用，解题的关键是：（1）找准等量关系，正确列出二元一次方程组；（2）根据各数量之间的关系，正确列出一元一次不等式．
18、AB=9+4.
【解析】
作CD⊥AB于D，据含30度的直角三角形三边的关系得到CD=，AD=9，再在Rt△BCD中根据正切的定义可计算出BD，然后把AD与BD相加即可．
【详解】
解：如图，过点C作CD⊥AB于点D．
∵在Rt△CDA中，∠A=30°，
∴CD=AC•sin30°=3，AD=AC×cs30°=9，
∵在Rt△CDB中，
∴BD===4．
∴AB=AD+DB=9+4.
本题考查了解直角三角形．解题时，通过作CD⊥AB于D构建Rt△ACD、Rt△BCD是解题关键．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、1
【解析】
首先根据已知易求CD=1，利用角平分线的性质可得点D到AB的距离是1．
【详解】
∵BC=6，BD=4，
∴CD=1.
∵∠C=90°，AD平分∠CAB，
∴点D到AB的距离=CD=1．
故答案为：1．
此题考查角平分线的性质：角平分线上的任意一点到角的两边距离相等；本题比较简单，属于基础题．
20、
【解析】
根据题意可得阴影部分的面积等于△ABC的面积，因为△ABC的面积是菱形面积的一半，根据已知可求得菱形的面积则不难求得阴影部分的面积．
【详解】
设AP，EF交于O点，
∵四边形ABCD为菱形，
∴BC∥AD,AB∥CD.
∵PE∥BC,PF∥CD，
∴PE∥AF,PF∥AE.
∴四边形AEFP是平行四边形．
∴S△POF=S△AOE.
即阴影部分的面积等于△ABC的面积．
∵△ABC的面积等于菱形ABCD的面积的一半，
菱形ABCD的面积=ACBD=5，
∴图中阴影部分的面积为5÷2=．
21、
【解析】
∵，∴8b=3(3a-b)，即9a=11b，∴，
故答案为.
22、1．
【解析】
根据正方形的性质可得出AB=AD、∠BAD=90°，由AB=AG、∠AGB=70°利用等腰三角形的性质及三角形内角和定理可求出∠BAG的度数，由∠DAG=90°-∠BAG可求出∠DAG的度数，由等腰三角形的性质结合三角形内角和定理可求出∠AGD的度数，再由∠BGD=∠AGB+∠AGD可求出∠BGD的度数．
【详解】
∵四边形ABCD为正方形，
∴AB＝AD，∠BAD＝90°．
∵AB＝AG，∠AGB＝70°，
∴∠BAG＝180°﹣70°﹣70°＝40°，
∴∠DAG＝90°﹣∠BAG＝50°，
∴∠AGD＝（180°﹣∠DAG）＝65°，
∴∠BGD＝∠AGB+∠AGD＝1°．
故答案为：1．
本题考查了正方形的性质、等腰三角形的性质以及三角形内角和定理，根据等腰三角形的性质结合三角形内角和定理求出∠AGD的度数是解题的关键．
23、1．
【解析】
根据众数的定义来判断即可，众数：一组数据中出现次数最多的数据叫做众数.
【详解】
解：数据1出现了3次，次数最多，所以这组数据的众数是1．
故答案为：1．
众数的定义是本题的考点，属于基础题型，熟练掌握众数的定义是解题的关键.
二、解答题（本大题共3个小题，共30分）
24、（1）证明见解析；（2）当AC＝AB时，四边形DEFG为正方形，证明见解析
【解析】
（1）利用三角形中位线定理推知ED∥FG，ED＝FG，则由“对边平行且相等的四边形是平行四边形”证得四边形DEFG是平行四边形，同理得EF＝HA＝BC＝DE，可得结论；
（2）AC＝AB时，四边形DEFG为正方形，通过证明△DCB≌△EBC（SAS），得HC＝HB，证明对角线DF＝EG，可得结论．
【详解】
（1）证明：∵D、E分别为AC、AB的中点，
∴ED∥BC，ED＝BC．
同理FG∥BC，FG＝BC，
∴ED∥FG，ED＝FG，
∴四边形DEFG是平行四边形，
∵AE＝BE，FH＝BF，
∴EF＝HA，
∵BC＝HA，
∴EF＝BC＝DE，
∴▱DEFG是菱形；
（2）解：猜想：AC＝AB时，四边形DEFG为正方形，
理由是：∵AB＝AC，
∴∠ACB＝∠ABC，
∵BD、CE分别为AC、AB边上的中线，
∴CD＝AC，BE＝AB，
∴CD＝BE，
在△DCB和△EBC中，
∵
∴△DCB≌△EBC（SAS），
∴∠DBC＝∠ECB，
∴HC＝HB，
∵点G、F分别为HC、HB的中点，
∴HG＝HC，HF＝HB，
∴GH＝HF，
由（1）知：四边形DEFG是菱形，
∴DF＝2FH，EG＝2GH，
∴DF＝EG，
∴四边形DEFG为正方形．
故答案为（1）证明过程见解析；（2）当AC＝AB时，四边形DEFG为正方形.
本题考查了平行四边形、矩形的判定、菱形的判定、正方形的判定、三角形的中位线性质定理，三角形中线的性质及等腰三角形的性质，其中三角形的中位线的性质定理为证明线段相等和平行提供了依据．
25、20米.
【解析】
过C作CE⊥AB于E，首先证明四边形CDBE为矩形，可得BD=CE=21，CD=BE=2，设AE=x，则=，求出x即可解决问题．
【详解】
如图，过C作CE⊥AB于E．
∵CD⊥BD，AB⊥BD， ∴∠EBD=∠CDB=∠CEB=90°，∴四边形CDBE为矩形，
∴BD=CE=21 ，CD=BE=6 ，设AE=x ， 则=，解得：x=1．
故旗杆高AB=AE+BE=1+6=20 (米)．
答：旗杆的高度为20米．
本题考查了相似三角形的应用，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用物长：影长=定值，构建方程解决问题，属于中考常考题型．
26、（1）y＝－2x＋12，点C坐标（4，4）；（2）画图形见解析，点D坐标（－4，1）；（3）点P的坐标（，）
【解析】
（1）由已知的等式可求得m、n的值，于是可得直线AB的函数解析式，把点C的坐标代入可求得a的值，由此即得答案；
（2）画出图象，由CD⊥AB知可设出直线CD的解析式，再把点C代入可得CD的解析式，进一步可求D点坐标；
（3）如图2，取点F（－2，8），易证明CE⊥CF且CE＝CF，于是得∠PEC＝45°，进一步求出直线EF的解析式，再与直线AB联立求两直线的交点坐标，即为点P.
【详解】
解：（1）∵＋（n﹣12）2＝1，
∴m＝6，n＝12，
∴A（6，1），B（1，12），
设直线AB解析式为y＝kx＋b，
则有，解得，
∴直线AB解析式为y＝－2x＋12，
∵直线AB过点C（a，a），
∴a＝－2a＋12，∴a＝4，
∴点C坐标（4，4）．
（2）过点C作CD⊥AB交x轴于点D，如图1所示，
设直线CD解析式为y＝x＋b′，把点C（4，4）代入得到b′＝2，
∴直线CD解析式为y＝x＋2，
∴点D坐标（－4，1）．
（3）如图2中，取点F（－2，8），作直线EF交直线AB于P，
图2
∵直线EC解析式为y＝x－2，直线CF解析式为y＝－x＋，
∵×（－）＝－1，
∴直线CE⊥CF，
∵EC＝2，CF＝2，
∴EC＝CF，
∴△FCE是等腰直角三角形，
∴∠FEC＝45°，
∵直线FE解析式为y＝－5x－2，
由解得，
∴点P的坐标为（）.
本题是一次函数的综合题，综合考查了坐标系中两直线的垂直问题、两条直线的交点问题和求特殊角度下的直线解析式，并综合了勾股定理和等腰直角三角形的判定和性质，解题的关键是熟知坐标系中两直线垂直满足，一次函数的交点与对应方程组的解的关系.其中，第（3）小题是本题的难点，寻找到点F（－2，8）是解题的突破口.
题号
一
二
三
四
五
总分
得分
批阅人
温度/℃
22
24
26
29
天数
2
1
3
1