2024年广东省梅州市九年级数学第一学期开学经典试题【含答案】

这是一份2024年广东省梅州市九年级数学第一学期开学经典试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）某校计划修建一条500米长的跑道，开工后每天比原计划多修15米，结果提前2天完成任务．如果设原计划每天修x米，那么根据题意可列出方程（ ）
A．＝2B．＝2
C．＝2D．＝2
2、（4分）顺次连接四边形四条边的中点，所得的四边形是菱形，则原四边形一定是( )
A．平行四边形B．对角线相等的四边形
C．矩形D．对角线互相垂直的四边
3、（4分）如图,在平面直角坐标系中,▱MNEF的两条对角线ME,NF交于原点O,点F的坐标是(3,2),则点N的坐标为( )
A．(-3,-2)B．(-3,2)C．(-2,3)D．(2,3)
4、（4分）下列四组线段中，能组成直角三角形的是
A．，，B．，，
C．，，D．，，
5、（4分）下列各式：中，分式的有（ ）
A．1 个B．2 个C．3 个D．4 个
6、（4分）学习了正方形之后，王老师提出问题：要判断一个四边形是正方形，有哪些思路？
甲同学说：先判定四边形是菱形，再确定这个菱形有一个角是直角；
乙同学说：先判定四边形是矩形，再确定这个矩形有一组邻边相等；
丙同学说：判定四边形的对角线相等，并且互相垂直平分；
丁同学说：先判定四边形是平行四边形，再确定这个平行四边形有一个角是直角并且有一组邻边相等．
上述四名同学的说法中，正确的是（）
A．甲、乙B．甲、丙C．乙、丙、丁D．甲、乙、丙、丁
7、（4分）如图，∠1，∠2，∠3，∠4，∠5是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=75°，则∠AED的度数是（ ）
A．120°B．110°C．115°D．100°
8、（4分）下列四个圆形图案中，分别以它们所在圆的圆心为旋转中心，顺时针旋转120°后，能与原图形完全重合的是（ ）
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）当x＝________时，分式的值为零．
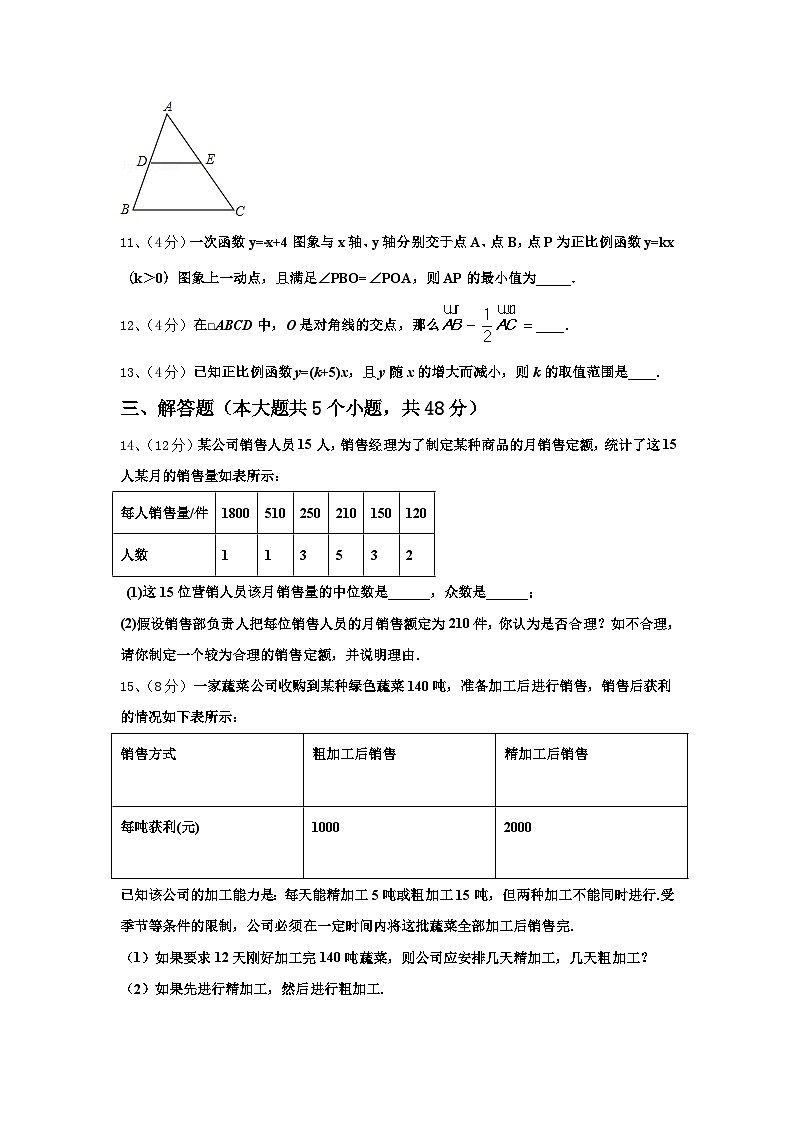
10、（4分）如图，△ABC中，D，E分别为AB，AC的中点，∠B=70°，则∠ADE= 度．
11、（4分）一次函数y=﹣x+4图象与x轴、y轴分别交于点A、点B，点P为正比例函数y=kx（k＞0）图象上一动点，且满足∠PBO=∠POA，则AP的最小值为_____．
12、（4分）在□ABCD中，O是对角线的交点，那么____．
13、（4分）已知正比例函数y=(k+5)x，且y随x的增大而减小，则k的取值范围是____.
三、解答题（本大题共5个小题，共48分）
14、（12分）某公司销售人员15人，销售经理为了制定某种商品的月销售定额，统计了这15人某月的销售量如表所示：
(1)这15位营销人员该月销售量的中位数是______，众数是______；
(2)假设销售部负责人把每位销售人员的月销售额定为210件，你认为是否合理？如不合理，请你制定一个较为合理的销售定额，并说明理由．
15、（8分）一家蔬菜公司收购到某种绿色蔬菜140吨，准备加工后进行销售，销售后获利的情况如下表所示：
已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行.受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售完.
（1）如果要求12天刚好加工完140吨蔬菜，则公司应安排几天精加工，几天粗加工？
（2）如果先进行精加工，然后进行粗加工.
①试求出销售利润元与精加工的蔬菜吨数之间的函数关系式；
②若要求在不超过10天的时间内，将140吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多获得多少利润？此时如何分配加工时间？
16、（8分）解方程
（1）+=3 （2）
17、（10分）如图，在平面直角坐标系中，矩形OABC的顶点A在y轴的正半轴上，点C在x轴的正半轴上，线段OA，OC的长分别是m，n且满足，点D是线段OC上一点，将△AOD沿直线AD翻折，点O落在矩形对角线AC上的点E处.
(1)求OA，OC的长；
(2)求直线AD的解析式；
(3)点M在直线DE上，在x轴的正半轴上是否存在点N，使以M、A、N、C为顶点的四边形是平行四边形?若存在，请直接写出点N的坐标；若不存在，请说明理由.
18、（10分）如图，在矩形中，是上一点，垂直平分，分别交、、于点、、，连接、.
(1)求证：；
(2)求证：四边形是菱形；
(3)若，为的中点，，求的长.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）直角三角形的两边为3和4，则该三角形的第三边为__________．
20、（4分）已知一个样本中共5个数据，其中前四个数据的权数分别为0.2，0.3，0.2，0.1，则余下的一个数据对应的权数为________．
21、（4分）如图，函数y＝bx和y＝ax＋4的图象相交于点A（1，3），则不等式bx＜ax＋4的解集为________．
22、（4分）如图，已知在Rt△ABC中，∠A＝90°，AB＝3，BC＝5，分别以Rt△ABC三条边为直径作半圆，则图中阴影部分的面积为_____．
23、（4分）已知：一组邻边分别为和的平行四边形，和的平分线分别交所在直线于点，，则线段的长为________．
二、解答题（本大题共3个小题，共30分）
24、（8分）在图1，图2中，点E是矩形ABCD边AD上的中点，请用无刻度的直尺按下列要求画图（保留画图痕迹，不写画法）
（1）在图1中，以BC为一边画△PBC，使△PBC的面积等于矩形ABCD的面积．
（2）在图2中，以BE、ED为邻边画▱BEDK．
25、（10分）如图，在平行四边形ABCD中，对角线AC与BD相交于点O，AB＝5，AD＝3，E是AB上的一点，F是AD上的一点，连接BO和FO．
（1）当点E为AB中点时，求EO的长度；
（2）求线段AO的取值范围；
（3）当EO⊥FO时，连接EF．求证：BE+DF＞EF．
26、（12分）如图1，在正方形ABCD中，P是对角线BD上的点，点E在AB上，且PA=PE．
（1）求证：PC=PE；
（2）求∠CPE的度数；
（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，试探究∠CPE与∠ABC之间的数量关系，并说明理由．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、A
【解析】
设原计划每天修x米，则实际每天修（x+15）米，根据时间=工作总量÷工作效率结合提前1天完成任务，即可得出关于x的分式方程，此题得解．
【详解】
设原计划每天修x米，则实际每天修（x+15）米．
由题意，知原计划用的时间为天，实际用的时间为：天，
故所列方程为：＝1．
故选：A．
本题考查了由实际问题抽象出分式方程，根据等量关系结合分式方程，找出未知数代表的意义是解题的关键．
2、B
【解析】
试题分析：根据三角形中位线的性质及菱形的性质，可证四边形的对角线相等．
解：如图所示，
∵四边形EFGH是菱形，
∴EH=FG=EF=HG=BD=AC，
故AC=BD.
即原四边形的对角线相等.
故选B.
点睛：本题主要考查中点四边形.画出图形，并利用三角形中位线与菱形的性质是解题的关键.
3、A
【解析】
对于平行四边形MNEF，点N的对称点即为点F，所以点F到X轴的距离为2，到Y轴的距离为1．即点N到X、Y轴的距离分别为2、1，且点N在第三象限，所以点N的坐标为（—1，—2）
4、D
【解析】
由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．
【详解】
A.1²+2²≠3²，故不是直角三角形，故本选项错误；
B.2²+3²≠4²故不是直角三角形，故本选项错误；
C.2²+4²≠5²，故不是直角三角形，故本选项错误；
D.3²+4²=5 ²，故是直角三角形，故本选项正确．
故选D．
本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
5、B
【解析】
根据分式定义：一般地，如果A，B表示两个整式，并且B中含有字母，那么式子叫做分式进行分析即可．
【详解】
是分式，共2个，故选：B.
本题考查分式的定义，解题的关键是掌握分式的定义.
6、D
【解析】
根据正方形的判定方法进行解答即可．正方形的判定定理有：对角线相等的菱形；对角线互相垂直的矩形；对角线互相垂直平分且相等的四边形．
【详解】
解：甲同学说：先判定四边形是菱形，再确定这个菱形有一个角是直角；
有一个角为直角的菱形的特征是：四条边都相等，四个角都是直角，则该菱形是正方形．故说法正确；
乙同学说：先判定四边形是矩形，再确定这个矩形有一组邻边相等；有一组邻边相等的矩形的特征是：四条边都相等，四个角都是直角．则该矩形为正方形．故说法正确；
丙同学说：判定四边形的对角线相等，并且互相垂直平分；对角线相等且互相垂直平分的四边形是正方形．故说法正确；
丁同学说：先判定四边形是平行四边形，再确定这个平行四边形有一个角是直角并且有一组邻边相等．有一个角是直角的平行四边形是矩形，有一组邻边相等的矩形是正方形．故说法正确；
故选D．
本题考查正方形的判定定理，熟记这些判定定理才能够正确做出判断．
7、A
【解析】
根据多边形的外角和求出∠5的度数，然后根据邻补角的和等于180°列式求解即可．
详
【详解】
解：∵∠1=∠2=∠3=∠4=75°，
∴∠5=360°﹣75°×4=360°﹣300°=60°，
∴∠AED=180°﹣∠5=180°﹣60°=120°．
故选A．
本题考查了多边形的外角和等于360°的性质以及邻补角的和等于180°的性质，是基础题，比较简单．
8、A
【解析】
试题分析：A、最小旋转角度==120°；
B、最小旋转角度==90°；
C、最小旋转角度==180°；
D、最小旋转角度==72°；
综上可得：顺时针旋转120°后，能与原图形完全重合的是A．
故选A．
考点：旋转对称图形．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、3
【解析】
根据分式值为0的条件：分子为0，分母不为0，即可得答案.
【详解】
∵分式的值为零，
∴x-3=0,x+5≠0，
解得：x=3，
故答案为：3
本题考查分式值为0的条件，要使分式值为0，则分子为0，分母不为0；熟练掌握分式值为0的条件是解题关键.
10、1
【解析】
由题意可知DE是三角形的中位线，所以DE∥BC，由平行线的性质即可求出∠ADE的度数．
【详解】
∵D，E分别为AB，AC的中点，
∴DE是三角形的中位线，
∴DE∥BC，
∴∠ADE=∠B=1°，
故答案为1．
本题考查了三角形中位线的性质以及平行线的性质．
11、2﹣2
【解析】
如图所示：
因为∠PBO=∠POA，
所以∠BPO=90°，则点P是以OB为直径的圆上．
设圆心为M，连接MA与圆M的交点即是P，此时PA最短,
∵OA＝4，OM＝2，
∴MA＝
又∵MP＝2，AP＝MA－MP
∴AP＝．
12、
【解析】
由向量的平行四边形法则及相等向量的概念可得答案．
【详解】
解：因为：□ABCD，
所以，，
所以：．
故答案为：．
本题考查向量的平行四边形法则，掌握向量的平行四边形法则是解题的关键．
13、k