




初中数学人教版(2024)九年级上册24.1.2 垂直于弦的直径授课课件ppt
展开连接圆上任意两点的______叫做弦,经过______的弦叫做直径.如图,_______________是弦,_________是直径.
______任意两点间的部分叫做圆弧,简称弧.______半圆的弧叫做优弧;______半圆的弧叫做劣弧. 如图,___________________________是优弧,_____________________是劣弧, 是______.
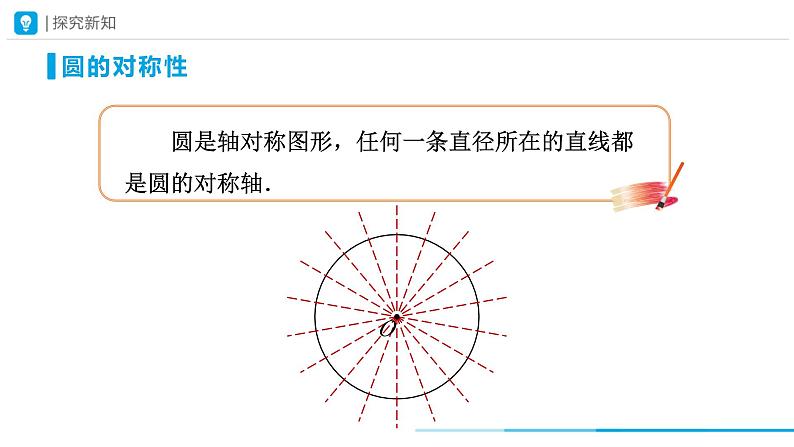
剪一个圆形纸片,沿着它的任意一条直径对折,重复做几次,你发现了什么?由此你能得出什么结论?你能证明你的结论吗?
圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴.
分析:要想证明这个结论,只需要证明圆上任意的一点关于直径所在直线(对称轴)的对称点也在圆上.
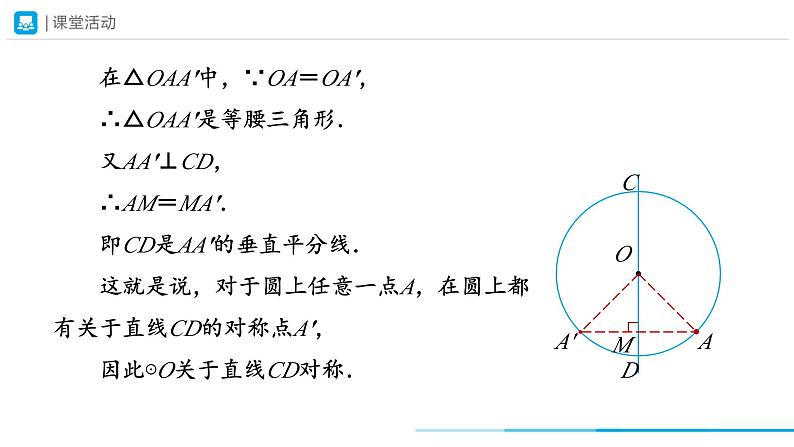
证明:如图,设CD是⊙O的任意一条直径,A 为⊙O上除点 C,D以外的任意一点.
过点 A 作AA′⊥CD,交⊙O于点A′,垂足为M,连接OA,OA′.
在△OAA′中,∵OA=OA′, ∴△OAA′是等腰三角形. 又AA′⊥CD, ∴AM=MA′. 即CD是AA′的垂直平分线. 这就是说,对于圆上任意一点A,在圆上都有关于直线CD的对称点A′, 因此⊙O关于直线CD对称.
如果我们在圆形纸片上任意画一条弦AB,如图,观察这个图形,它还是轴对称图形吗?若是,请找出它的对称轴.
如图,作出垂直于弦AB的直径CD,沿着这条直径所在的直线对折,图形在这条直径两侧的部分能完全重合,即图形关于这条直径所在直线对称.
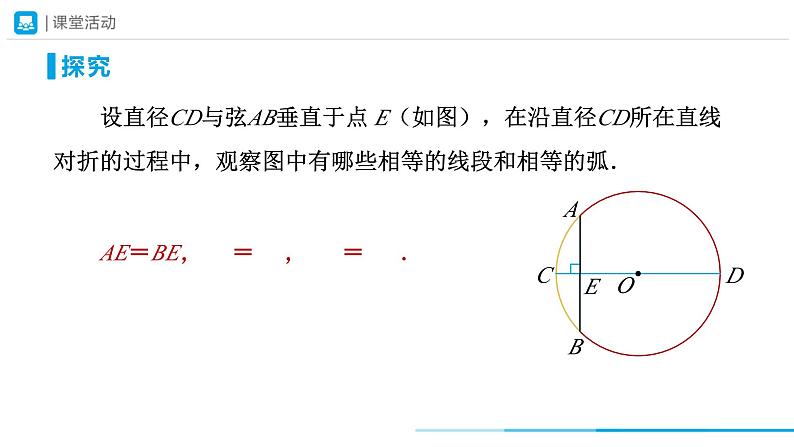
设直径CD与弦AB垂直于点 E(如图),在沿直径CD所在直线对折的过程中,观察图中有哪些相等的线段和相等的弧.
结合下面的动图,你能将你的发现归纳成一般结论吗?
符号语言: ∵CD是直径,AB为⊙O的弦,且CD⊥AB, 垂足为E. ∴AE=BE, = , = .
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
③平分弦④平分弦所对的优弧⑤平分弦所对的劣弧
在这个定理中, ①过圆心,②垂直于弦,这两个条件缺一不可,同时满足这两个条件时才能推出结论③平分弦,④平分弦所对的优弧,⑤平分弦所对的劣弧.
反过来,平分弦的直径一定垂直于这条弦吗?
请在纸上画一个以点O为圆心的圆,在⊙O上任意画出一条弦CD(不是直径).找到弦CD的中点 E,过点 E 作⊙O的直径MN,MN与CD有什么位置关系?
测量∠MED的度数,得∠MED=90°,即MN⊥CD.
如果弦CD是直径呢?
两条直径任何时候都是互相平分的,但是不一定相互垂直.
猜想:如果有一条直径平分一条不是直径的弦,那么它就能垂直于这条弦,也能平分这条弦所对的两条弧.
你能对猜想进行证明吗?
已知:如图,⊙O的直径CD交弦AB(不是直径)于点P,AP=BP.求证:CD⊥AB, = , = .
证明:连接OA,OB,则AO=BO.
∴△AOB是等腰三角形. ∵AP=BP, ∴CD⊥AB , ∴ = , = (垂直于弦的直径平分弦所对的两条弧).
符号语言: ∵在⊙O中,CD是直径,弦AB不是直径,且AE=BE, ∴CD⊥AB, = , = .
垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
②垂直于弦④平分弦所对的优弧⑤平分弦所对的劣弧
在这个推论中,“③平分弦”的“弦”一定是非直径的弦,否则命题就不一定成立.
例1 如图,在⊙O中,弦AB的长为 8 cm,圆心 O 到AB的距离为 3 cm,求⊙O的半径.
在Rt△OEA中,由勾股定理,得
∴OA=5,即⊙O的半径为 5 cm.
OA2=42+32,
解:过点 O 作OE⊥AB,垂足为 E,连接OA.
∵OE⊥AB,AB=8 cm,
例2 如图, M 是⊙O中的弦CD的中点,EM经过圆心 O 交⊙O于点 E,并且CD=6 cm,EM=9 cm,求⊙O的半径.
在Rt△OCM中,由勾股定理,得
解得r=5,即⊙O的半径为 5 cm.
r2=(9-r)2+32,
解:如图,连接OC.设OC=r cm,则OM=(9-r)cm.
∵EM经过圆心 O,M是CD的中点,CD=6 cm,
1.四变量:如图,弦长a,圆心到弦的距离d,半径r,弧的中点到弦的距离(弓形高)h,已知这四个变量中的任意两个可求其他两个.
2.两关系:(1) +d2=r2; (2)h+d=r.
垂径定理基本图形的四变量、两关系
例3 赵州桥是我国隋代建造的石拱桥,距今约有1 400年的历史,是我国古代人民勤劳与智慧的结晶.它的主桥拱是圆弧形,它的跨度(弧所对的弦的长)为 37 m,拱高(弧的中点到弦的距离)为 7.23 m,求赵州桥主桥拱的半径(结果保留小数点后一位).
分析:解决此问题的关键是根据赵州桥的实物图画出几何图形.
根据垂径定理,D是AB的中点,C 是 的中点,CD就是拱高.
由题设可知 AB=37,CD=7.23, ∴AD= AB= ×37=18.5, OD=OC-CD=R-7.23, 在Rt△OAD中,由勾股定理,得 OA2=AD2+OD2, 即 R2=18.52+(R-7.23)2. 解得 R≈27.3. 因此,赵州桥的主桥拱半径约为 27.3 m.
用数学语言描述已知和未知
观察垂径定理及其推论的题设与结论,你能发现什么?
对于一个圆和一条直线,如果具备下列五个条件中的任意两个,那么一定具备其他三个: ①过圆心;②垂直于弦;③平分弦(非直径);④平分弦所对的优弧;⑤平分弦所对的劣弧. 简记为“知二推三”.
与垂径定理有关的常用结论: (1)平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧. (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧.
初中数学人教版(2024)九年级上册24.1.2 垂直于弦的直径教课课件ppt: 这是一份初中数学人教版(2024)九年级上册<a href="/sx/tb_c88762_t3/?tag_id=26" target="_blank">24.1.2 垂直于弦的直径教课课件ppt</a>,共27页。PPT课件主要包含了学习目标,导入新课,问题情境,折一折,讲授新课,用折叠的方法,说一说,线段AEBE,垂径定理,∴AEBE等内容,欢迎下载使用。
数学九年级上册第二十四章 圆24.1 圆的有关性质24.1.2 垂直于弦的直径多媒体教学ppt课件: 这是一份数学九年级上册第二十四章 圆24.1 圆的有关性质24.1.2 垂直于弦的直径多媒体教学ppt课件,共9页。PPT课件主要包含了学习目标,自学指导,自学检测,8cm,解8米,小组合作,跟踪练习,课堂小结等内容,欢迎下载使用。
初中数学人教版九年级上册24.1.2 垂直于弦的直径评课ppt课件: 这是一份初中数学人教版九年级上册24.1.2 垂直于弦的直径评课ppt课件,共23页。PPT课件主要包含了活动一,探索发现,火眼金睛,借你慧眼,CD过圆心,CD⊥AB于E,AEBE,轻松过关,顺利闯二关,课堂练习等内容,欢迎下载使用。













