山西省实验中学2024-2025学年九年级上学期第一次月考数学试题

这是一份山西省实验中学2024-2025学年九年级上学期第一次月考数学试题，共9页。试卷主要包含了单项选择题，填空题，解答题等内容，欢迎下载使用。
九年级 数学
（本试卷满分100分，考试时间90分钟）
命题人：武杰 校对人：牛婷婷
一、单项选择题（本题共10个小题，每小题3分，共30分）
1．下列属于一元二次方程的是（ ）
A．B．C．D．
2．下列性质中菱形一定具有的是（ ）
A．对角线相等B．有一个角是直角C．对角线互相垂直D．四个角相等
3．已知关于的方程的一个根是2，则它的另一个根是（ ）
A．0B．1C．2D．3
4．某服装店购进一款印有“龖”字图案的上衣，据店长统计，该款上衣1月份销售量为150件，3月份销售量为216件，若该款上衣销售量的月平均增长率为，根据题意可列方程得（ ）
A．B．C．D．
5．下列方程中没有实数根的是（ ）
A．B．C．D．
6．如图，在菱形中，对角线与相交于点，，，则的长为（ ）
A．2B．3C．D．
7．如图，四边形是正方形，，，cm，cm，那么的长为（ ）
A．6cmB．6.5cmC．5.5cmD．4cm
8．根据下表得知估算一元二次方程的一个根的范围是（ ）
A．B．C．D．
9．给出一种运算：对于函数，规定，例如，若函数，则有，已知函数，则方程的解是（ ）
A．，B．C．，D．，
10．如图，在边长为4的正方形中，为边上的一点，且，点为对角线上的动点，则周长的最小值是（ ）
A．3B．4C．5D．6
二、填空题（本大题共6个小题，每小题3分，共18分）
11．方程化成一般形式是__________________.
12．如图，在矩形中，对角线，相交于点，点，分别是，的中点，若cm，cm，则的周长__________________cm.
13．如图，邻边不等的矩形花圃，它的一边利用已有的16m的围墙，另外三边所围的栅栏的总长度是32m，若矩形花圃的面积为120m2，则的长度是__________________m.
14．已知方程的两根分别为，，则的值为__________________.
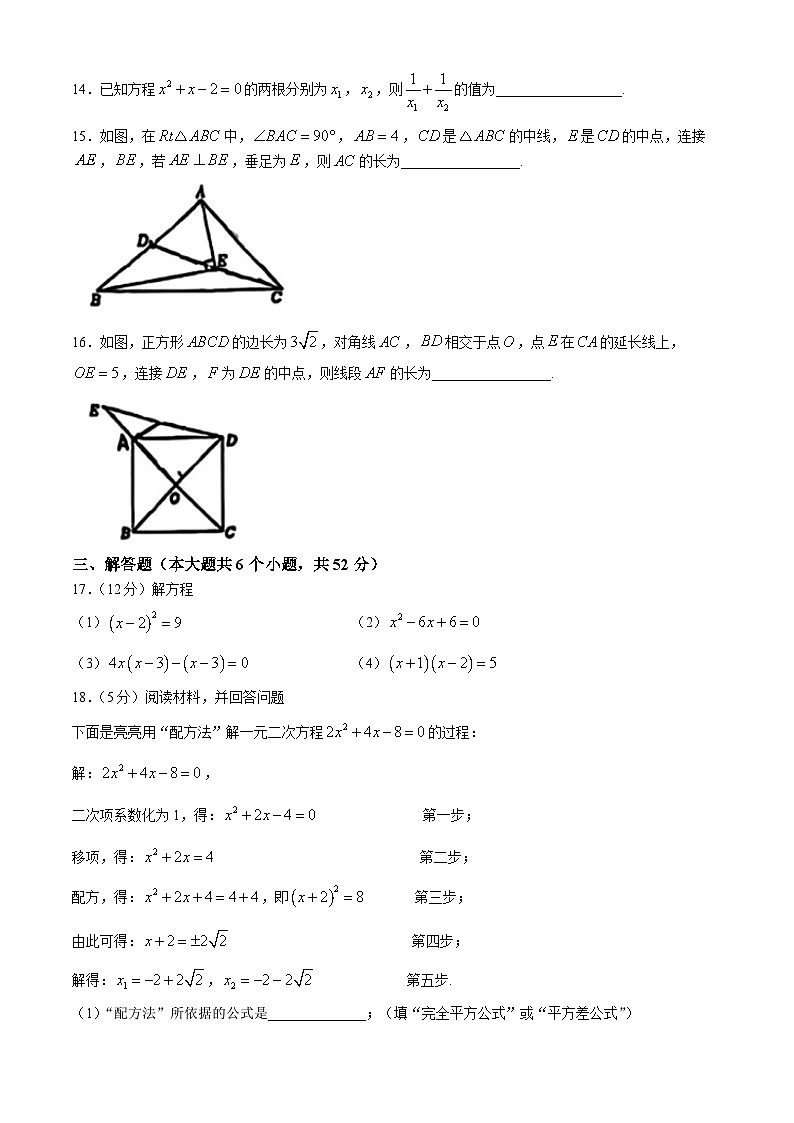
15．如图，在中，，，是的中线，是的中点，连接，，若，垂足为，则的长为_________________.
16．如图，正方形的边长为，对角线，相交于点，点在的延长线上，，连接，为的中点，则线段的长为_________________.
三、解答题（本大题共6个小题，共52分）
17．（12分）解方程
（1）（2）
（3）（4）
18．（5分）阅读材料，并回答问题
下面是亮亮用“配方法”解一元二次方程的过程：
解：，
二次项系数化为1，得： 第一步；
移项，得： 第二步；
配方，得：，即 第三步；
由此可得： 第四步；
解得：， 第五步.
（1）“配方法”所依据的公式是______________；（填“完全平方公式”或“平方差公式”）
（2）上面解答过程，从第_________步开始出现错误；
（3）写出正确的解答过程；
19．（6分）如图，已知矩形中，是对角线
（1）实践与操作：利用尺规作线段的垂直平分线，垂足为点，交边于点，交边于点（要求：尺规作图并保留作图痕迹，不写作法，标明字母）；
（2）猜想与证明：猜想线段与的数量关系，并加以证明.
20．（6分）已知：如图，在菱形中，对角线，相交于点，，.
（1）求证：四边形是矩形；
（2）若，，则四边形的面积是______________.
21．（12分）请根据以下素材，完成探究任务.
22．（11分）
已知正方形，点是射线上一动点（不与、重合），连接并延长交直线于点，交于点，连接，过点作交于点.
（1）若点在边上，如图1.
①证明：；
②猜想线段与的关系并说明理由；
（2）取中点，连结，若，正方形边长为6，直接写出的长.
山西省实验中学
2024-2025学年第一学期第一次阶段性测评答案（卷）
九年级 数学
一、选择题
1-5：CCABA
6-10：DBDCD
二、填空题
11．12．913．1014．
15．16．
三、解答题
17．
（1），（2），
（3），（4），
18．（1）完全平方公式
（2）三
（3）
解得，
19．（1）
如图所示，即为所求
（2），理由如下：
四边形是矩形
是的垂直平分线
20．（1）证明：，，
四边形是平行四边形，
四边形是菱形，
，
，
平行四边形是矩形；
（2）四边形是菱形，，，
，
，
由（1）得：四边形是矩形，
在中，
由勾股定理得：，
四边形的面积.
21．（1）
解得
答：款钥匙扣的进价为30元/件，款钥匙扣的进价为25元/件。
（2）①15
②12
获得的销售利润最大为1080元.
（3）设款钥匙扣的售价定为元，则每件的销售利润为
元，平均每天可售出件，
依题意得：，
整理得：，
解得：，.
答：将销售价定为每件30元或34元时，才能使款钥匙扣平均每天销售利润为90元.
22．证明：（1）①四边形是正方形，
，，
在和中，
，
，
；
②结论：，理由如下：
，
，
，
，
，
，，
，
，
，，
，
，
；
（2）①如图，当点在线段上时，连接.
，，
，
，
，
，，
，
在中，，
；
②如图，当点在线段的延长线上时，连接.
同法可知是的中位线，
，
在中，，
综上所述，的长为或.…
…
…
0.56
1.25
1.96
…
制定购买方案
购买背景
背景1
巴黎奥运会期间，某网店直接从工厂购进，两款吉祥物“弗里吉”钥匙扣样式，网店第一次用850元购进款钥匙扣20件、款钥匙扣10件，且每件比每件贵5元.
背景2
款钥匙扣售价为45元/件，款钥匙扣售价为37元/件，第一次购进的“弗里吉”钥匙扣售完后，该网店计划再次购进、两款“弗里吉”钥匙扣共80件（进货价和售价均不变），且进货总价不高于2200元.
背景3
巴黎奥运会临近结束时，网店打算把款钥匙扣调价销售，如果按照原价销售，平均每天可销售4件，经过调查发现，销售价每降价1元，平均可多售2件.
信息整理
若款钥匙扣的进价为元/件，款钥匙扣的进价为元/件，列表如下：
类别
款钥匙扣
款钥匙扣
进货量（件）
20
10
进价（元/件）
售价（元/件）
45
37
单件利润（元/件）
①
②
探究任务
任务1
求两款钥匙扣的进价
任务2
请完成填空①和②，根据背景2中的信息，获得的销售利润最大为_______元.
任务3
网店要使款钥匙扣的销售利润平均每天达到90元，每件款钥匙扣的定价应为多少元？