北师大版（2024）八年级上册3 勾股定理的应用教案

这是一份北师大版（2024）八年级上册3 勾股定理的应用教案，共6页。
1.能正确运用勾股定理及其逆定理解决简单的实际问题,进一步发展应用意识.
2.能熟练运用勾股定理求最短距离.
3.通过问题情境的设立,帮助学生体会数学来源于生活,又应用于生活,积累利用勾股定理的知识解决生活中实际问题的经验和方法.
学习重点
利用勾股定理解决立体图形上的最短距离问题.
学习难点
把立体图形转化成平面图形,在实际问题中构造直角三角形并解决问题.
课时活动设计
回顾引入
1.勾股定理的内容是什么?
2.勾股定理逆定理的内容是什么?
3.我们学过哪些关于“最短”的知识?
设计意图:教师通过回顾已学的相关知识,引出本节课所学内容.
探究新知
问题情境:蚂蚁和食物分别在圆柱体上相对的顶点处,求蚂蚁怎样走最近.
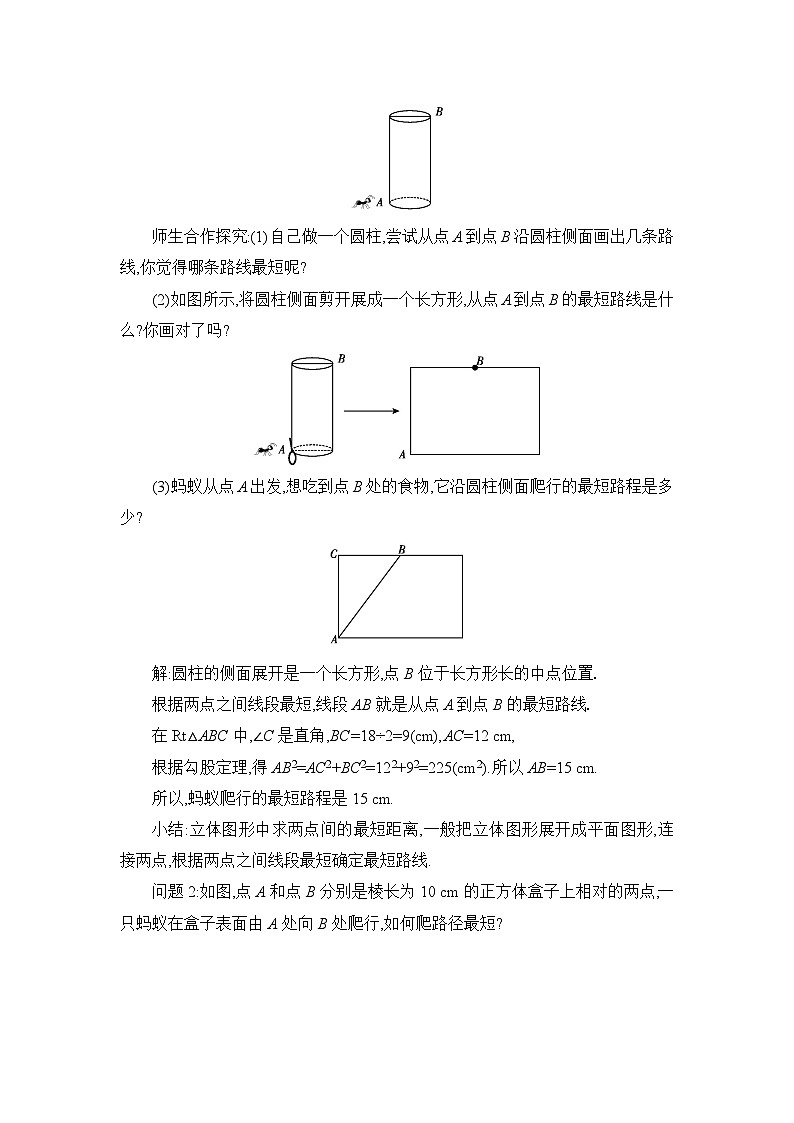
问题1:如图,蚂蚁从圆柱下底面边缘的点A沿圆柱的侧面爬到上底面的边缘B处,
(1)如何爬路径最短?
(2)若已知圆柱的高为12 cm,底面周长为18 cm,求最短路径.
师生合作探究:(1)自己做一个圆柱,尝试从点A到点B沿圆柱侧面画出几条路线,你觉得哪条路线最短呢?
(2)如图所示,将圆柱侧面剪开展成一个长方形,从点A到点B的最短路线是什么?你画对了吗?
(3)蚂蚁从点A出发,想吃到点B处的食物,它沿圆柱侧面爬行的最短路程是多少?
解:圆柱的侧面展开是一个长方形,点B位于长方形长的中点位置.
根据两点之间线段最短,线段AB就是从点A到点B的最短路线.
在Rt△ABC中,∠C是直角,BC=18÷2=9(cm),AC=12 cm,
根据勾股定理,得AB2=AC2+BC2=122+92=225(cm2).所以AB=15 cm.
所以,蚂蚁爬行的最短路程是15 cm.
小结:立体图形中求两点间的最短距离,一般把立体图形展开成平面图形,连接两点,根据两点之间线段最短确定最短路线.
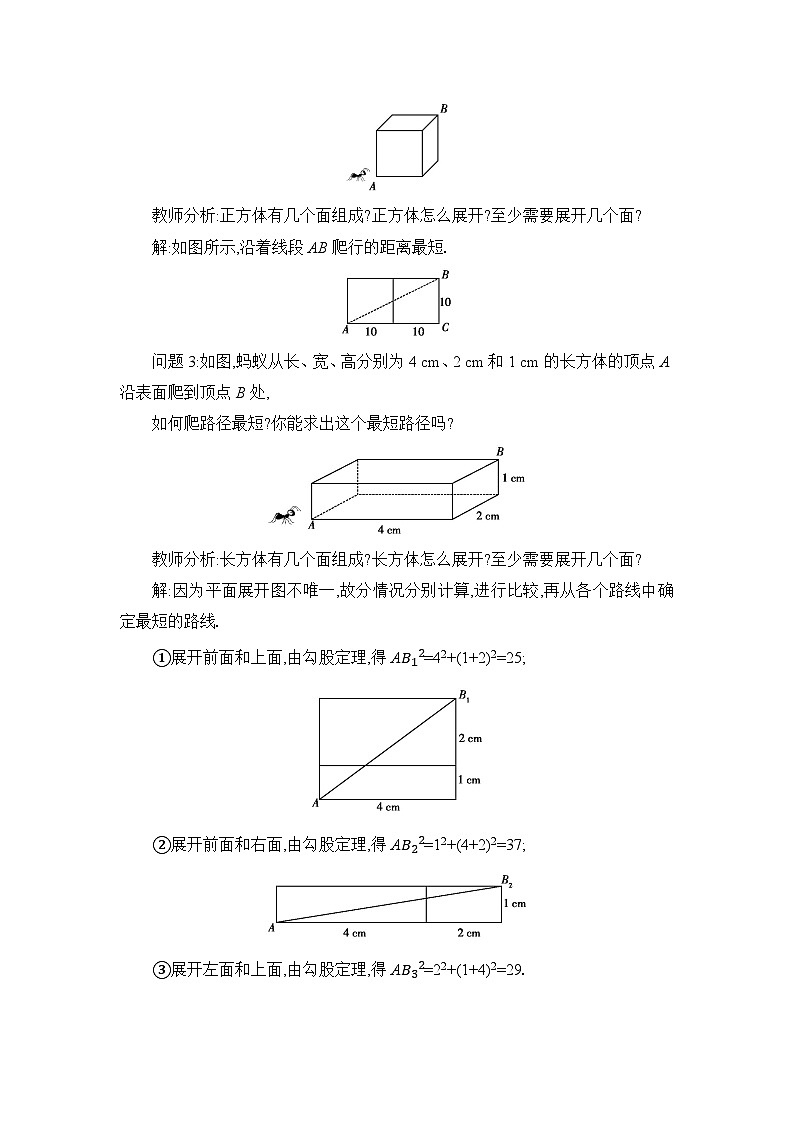
问题2:如图,点A和点B分别是棱长为10 cm的正方体盒子上相对的两点,一只蚂蚁在盒子表面由A处向B处爬行,如何爬路径最短?
教师分析:正方体有几个面组成?正方体怎么展开?至少需要展开几个面?
解:如图所示,沿着线段AB爬行的距离最短.
问题3:如图,蚂蚁从长、宽、高分别为4 cm、2 cm和1 cm的长方体的顶点A沿表面爬到顶点B处,
如何爬路径最短?你能求出这个最短路径吗?
教师分析:长方体有几个面组成?长方体怎么展开?至少需要展开几个面?
解:因为平面展开图不唯一,故分情况分别计算,进行比较,再从各个路线中确定最短的路线.
①展开前面和上面,由勾股定理,得AB12=42+(1+2)2=25;
②展开前面和右面,由勾股定理,得AB22=12+(4+2)2=37;
③展开左面和上面,由勾股定理,得AB32=22+(1+4)2=29.
因为37>29>25,所以AB1最短,最短路径AB1为5 cm.
学生自主完成教材第13页做一做,教师进行点评.
设计意图:本环节在圆柱体的基础上依次增加难度,先是变为正方体,再变为长方体,引导学生由浅入深,由圆柱体侧面展开一个面上的最短距离.到正方体再到长方体展开两个面才能找到最短距离;引导学生理解长方体有六种展开方式的原因(源于长,宽,高的组合),通过勾股定理计算比较得出最短距离.本环节很好地渗透了分类讨论思想.
典例精讲
例 如图是一个滑梯示意图,若将滑道AC水平放置,则刚好与AB一样长,已知滑梯的高度CE=3 m, CD=1 m,试求滑道AC的长.
解:设滑道AC的长度为x m,则AB的长度为x m, AE的长度为(x-1) m.
在Rt△ACE中,∠AEC= 90°,由勾股定理,得AE2+CE2=AC2,
即(x-1)2+32=x2,解得x=5.
故滑道AC的长度为5 m.
设计意图:通过例题讲解,及时巩固所学.
巩固训练
1.如图,一圆柱高8 cm,底面半径为6π cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是 10 cm .
2.如图所示,一只蚂蚁在长方体(长10 cm,宽5 cm,高20 cm)的底面上的点A处,蚂蚁想吃到与点A相对的点C'处的食物,需要爬行的最短路程是多少?
解:①展开前面和右面,得到长方形ACC'A',如图1.在长方形ACC'A'中, AC=15 cm, CC'=20 cm,则AC'2= AC2+CC'2=152+202=625;
②展开前面和上面,得到长方形ABC'D',如图2.在长方形ABC'D'中, AB=10 cm, BC'=25 cm,则AC'2=AB2+BC'2=102+252=725;
③展开左面和上面,得到长方形AB'C'D,如图3.在长方形AB'C'D中,AB'=30 cm,B'C'=5 cm,则AC'2=AB'2+B'C'2=302+52=925;
因为925>725>625 ,所以最短AC'=25 cm,所以蚂蚁需要爬行的最短路程是25 cm.
图1 图2 图3
设计意图:进一步巩固本节课所学内容,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
课堂小结
1.本节课我们学到了哪些内容?
2.如何解决最短路径问题?我们应注意什么?
设计意图:以提问的形式让学生复述本节课所学知识,加强学生对知识的理解和掌握,培养分析问题,解决问题的能力.
课堂8分钟.
1.教材第14页随堂练习,习题1.4第1,2,3,4题.
2.七彩作业.
1.3 勾股定理的应用
1.勾股定理
直角三角形两直角边的平方和等于斜边的平方.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
2.勾股定理的应用
(1)最短路径问题:把立体图形转化为平面图形,构造出直角三角形,利用勾股定理来解决最短路径问题.
(2)利用勾股定理逆定理来判断实际问题中是否垂直.
教学反思