黑龙江省哈尔滨市双城区乐群乡中学2024-2025学年八年级上学期9月月考数学试题

这是一份黑龙江省哈尔滨市双城区乐群乡中学2024-2025学年八年级上学期9月月考数学试题，共12页。试卷主要包含了选择题必须使用2B铅笔填涂，尺规作图作的平分线方法如下，下列说法中等内容，欢迎下载使用。

考生须知：
1.本试卷满分为120分，考试时间为120分钟.
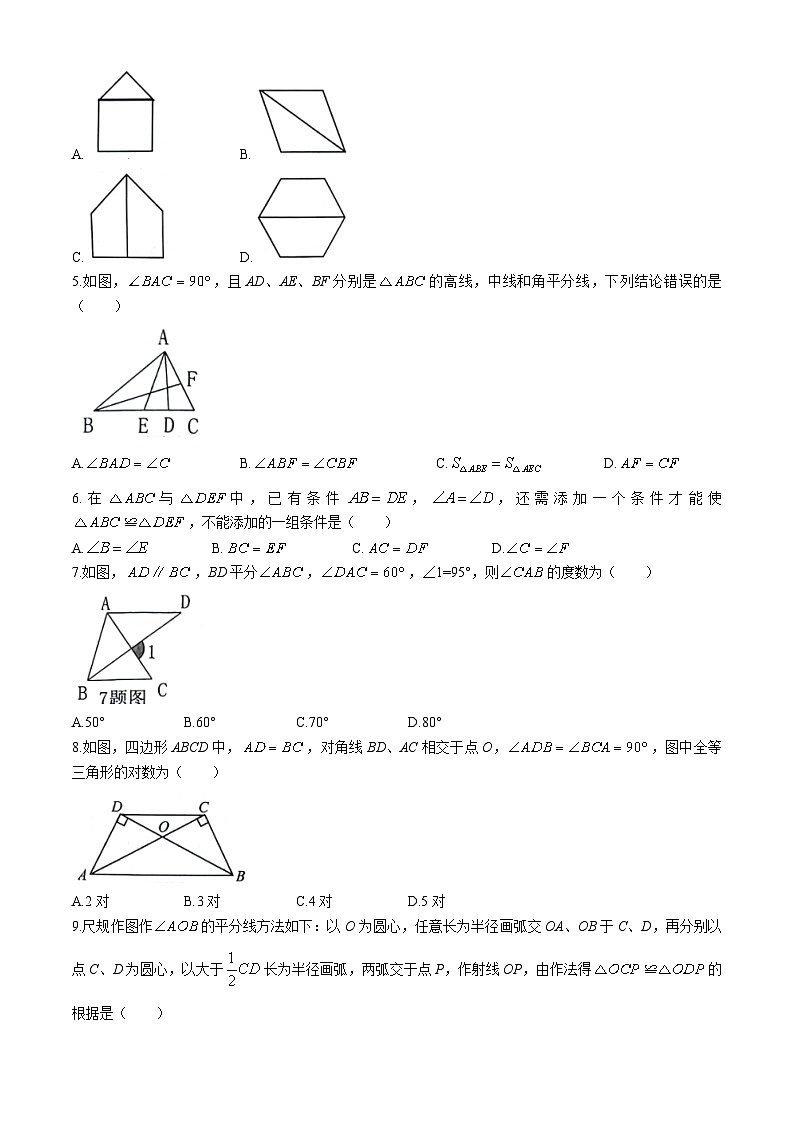
2.答题前，考生先将自己的“姓名”、“考号”、“考场”、“座位号”在答题卡上填写清楚，将“条形码”准确粘贴在条形码区域内.
3.请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题纸上答题无效.
4.选择题必须使用2B铅笔填涂：非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚.
5.保持卡面整洁，不要折叠、不要弄脏、弄皱，不准使用涂改液、刮纸刀.
第I卷选择题（共30分）（涂卡）
一、选择题（每题3分，计30分，每题只有一个正确的答案）
1.以下列各组线段为边，能组成三角形的是（ ）
A.2，3，5B.5，5，10C.3，4，6D.4，5，11
2.图中共有三角形的个数是（ ）
A.4B.5C.6D.7
3.下列各图形中，分别是四位同学所画的中BC边上的高AE，其中正确的是（ ）
A.B.
C.D.
4.下列各图中具有稳定性的是（ ）
A.B.
C.D.
5.如图，，且AD、AE、BF分别是的高线，中线和角平分线，下列结论错误的是（ ）
A.B.C.D.
6.在与中，已有条件，，还需添加一个条件才能使，不能添加的一组条件是（ ）
A.B.C.D.
7.如图，，BD平分，，∠1=95°，则的度数为（ ）
A.50°B.60°C.70°D.80°
8.如图，四边形ABCD中，，对角线BD、AC相交于点O，，图中全等三角形的对数为（ ）
A.2对B.3对C.4对D.5对
9.尺规作图作的平分线方法如下：以O为圆心，任意长为半径画弧交OA、OB于C、D，再分别以点C、D为圆心，以大于长为半径画弧，两弧交于点P，作射线OP，由作法得的根据是（ ）
A.SASB.ASAC.AASD.SSS
10.下列说法中：①如果一个三角形两个内角的差等于另一个内角，那么这个三角形是直角三角形；②三角形的外角等于两个内角的和；③两组边分别相等的两个直角三角形全等；④三角形中最大的内角不能小于60°；其中正确的个数是（ ）.
A.1个B.2个C.3个D.4个
第Ⅱ卷 非选择题（共90分）
二、填空题（每题3分，共24分）
11.已知三角形三边分别为2，x，5，则x的取值范围是_______.
12.一个多边形的每一个外角都等于60°，这个多边形的内角和是_______度.
13.已知等腰三角形的两边长分别为4cm和8cm，则等腰三角形的周长为________cm.
14.如图，中，，将其沿CD折叠，使点A落在边CB的延长线上的点E处，若，则_______度
15.如图中，于D，BE平分，，，的度数为_______度.
16.数学活动课上，丽丽在一个正方形内画正方形，她发现图中三角形的个数与所画正方形的数量之间存在某种规律，依此规律她推断出第2024个图形中正方形与三角形的数量之和为________.
17.已知中AE是角平分线，AD是BC边上的高线，，，则的度数为________.
18.如图，已知四边形ABCD的对角线AC、BD相交于点E，，，，的面积为18，则AD的长度为________.
三、解答题（19-23每题6分，24、25每题8分，26、27每题10分，共66分）
19.已知a、b、c是的三边，化简.
20.（1）某n边形的内角和与外角和的差为720°，求此多边形的边数；
（2）某n边形的每一个内角都等于144°，求这个多边形的内角和.
21.如图，已知中，，，于D，AE平分交CD于F.求和的度数.
22.如图，将直角三角形的一个顶点放在正方形ABCD的顶点A处，绕顶点A转动三角板，三角板的两边分别交正方形的DC边于E，交BC边于F，连接EF，.
求证：
23.如图，平面直角坐标系中的每个小正方形的边长均为1个单位长度，的三个顶点均在小正方形的格点上.
（1）将向左平移6个单位，再向上平移1个单位到的位置，请画出；
（2）以AB为边在网格中确定点D，连接AD、BD，使与全等.请画出.
24.如图，点F、G为线段BC上两点，于F，于G，连接BD、CE，，.
（1）如图1，求证：；
（2）如图2，设BD与CE相交于点O，连接BE、CD并延长相交于点A，请直接写出图中4对全等的三角形.（除外）

24题图1 24题图2
25.鸿志中学传统文化兴趣小组在国庆节前夕，准备组织学生为学校编织大、小两种中国结装饰校园，若编织2个大号中国结和4个小号中国结需要彩绳22米，若编织1个大号中国结和3个小号中国结需要彩绳14米.
（1）求编织1个大号中国结和1个小号中国结各需要彩绳多少米?
（2）鸿志中学决定编织以上两种中国结共60个，编织这两种中国结的彩绳长不超过230米，那么该中学最多编织多少个大中国结?
26.（1）阅读理解
如图①，在中，若，，AD为BC边上的中线，则AD的取值范围是_______.
解决此问题可用如下方法：延长AD到K，使，再连接BK，这样就把AB、AC、转化到了中，利用三角形三边关系即可得出结论.
（2）实践探究
如图②在中，点D是BC边的中点，，DE交AB边于E，DF交AC边于F，连接EF，判断与EF的大小关系，并说明理由；
（3）拓展延伸
我们发现直角三角形三边之间存在一种关系，若直角三角形的两直角边分别为a、b，斜边为c，那么.等腰三角形顶角的平分线，底边上的高线和中线互相重合.如图③，在（2）的条件下，当，，的长度是关于x、y的方程组的两个根，求的面积.
27.在平面直角坐标系中，点在y轴上，点在x轴上，且b是不等式的最大整数解，且.
（1）求点A的坐标；
（2）动点E从点A出发，以每秒1个单位的速度沿y轴向下运动，动点F从点B出发，以每秒1个单位的速度沿x轴向右运动，E、F同时出发，运动时间为t秒，连接EF交直线AB于点P，作轴于H，请用含t的式子表示PH的长；（直接写出t的取值范围）
（3）在（2）的条件下，当时，以EF为斜边作等腰直角三角形EQF，其中，，求点Q的坐标.
2024-2025学年度上学期八年级第一次月考试题
数学试卷参考答案
一、选择题
二、填空题
18.略
三、解答题
19.解：原式
20.解：（1），，答：这个多边形的边数为8.
（2）多边形的每个外角为：180°-144°=36°，多边形的边数为：360°÷36°=10，10×144°=1440°，答：这个多边形的内角和为1440°.
或，，10×144°=1440°，
21.解：∵∴
∵∴
∵AE平分.∴
∴
∵于D∴
∴
22.证明：作于H，∴
∵ABCD为正方形∴，.
在和中
∴
∴，，∴，
在和中
∴，
∴，∴.
23.（1）画图正确；（2）画图正确.
24.（1）证明：∵∴，∴
∵于G，于F∴
在和中
∴.
（2），，，
25.（1）解：设编织1个大号中国结需要彩绳x米，编织1个小号中国结需要彩绳y米，根据题意得.
解得
答：编织1个大号中国结需要彩绳5米，编织1个小号中国结需要彩绳3米.
（2）设该中学编织m个大中国结，根据题意得
解得
答：该中学最多编织25个大中国结.
26.（1）
（2）延长FD到G，使，连接BG、GE.
∵D是BC中点，∴
在和中
∴
∴
∵，，∴
在和中
∴
∴
∵，∴.
（3）方法1.∵，，∴，，∴，
延长FD到K，使，连接BK、EK
由可得，
∵，∴，∴
由可得
∵，∴
∴
由，∴
∴，∴
方法2，∵，，∴，，∴，
连接，可得
∴，，，
∵，，∴
在和中
∴
∵，
∵，∴，
∵，∴.
27.解：（1）解不等式得，
∵b取最大整数∴
∵，∴，∴.
（2）①当时，，
作轴，交AB于C，轴于K，
∵，，
∴，∴
∴
∴
∵，
∴
∵PKOH为长方形，∴
∴
②当时，，
作轴，交AB于C，轴于K
∵，，
∴，∴
∴
∴.
∵，∴
∵PKOH为长方形，∴，∴.
（3）①当时，，，
Q在第一象限时，过点Q作轴于M，于N，
由，可得，
设，则，
∴，∴
∴.
②Q在第四象限时，过点Q作轴于M，轴于N，
由，可得，，
∴
设，，
∴，∴，
∴.


题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
C
B
D
B
A
B
D
B
题号
11
12
13
14
15
16
17
18
答案
720
20
40
55
10121
40°或80°
2