

2024-2025学年北京市海淀区中关村中学高二(上)开学数学试卷(含答案)
展开1.复数2i1−i(i是虚数单位)的虚部是( )
A. 1B. −iC. 2D. −2i
2.已知向量a=(−5,5),b=(0,−3),则a与b的夹角为( )
A. π4B. π3C. 2π3D. 3π4
3.已知函数f(x)=Acs(ωx+φ)(A>0,ω>0,−π2<φ<π2)的部分图象如图所示,则( )
A. ω=23,φ=−π6
B. ω=23,φ=π6
C. ω=43,φ=−π6
D. ω=43,φ=π6
4.已知csα=45,α∈(3π2,2π),则sinα2等于( )
A. − 1010B. 1010C. 310 3D. −35
5.若函数f(x)=2sin(ωx+π3)(ω>0)在区间[−π4,π4]上单调递增,则ω的取值范围是( )
A. (0,103]B. (0,23]C. [23,103]D. [103,+∞)
6.在△ABC中,角A,B,C的对边分别为a,b,c,已知∠B=30°,△ABC的面积为32,且sinA+sinC=2sinB,则b的值为( )
A. 4+2 3B. 4−2 3C. 3−1D. 3+1
7.若x,y∈R,则“lgx+lg(y−1)=0”是“x(y−1)=1”的( )
A. 充分不必要条件B. 必要不充分条件
C. 充分必要条件D. 既不充分也不必要条件
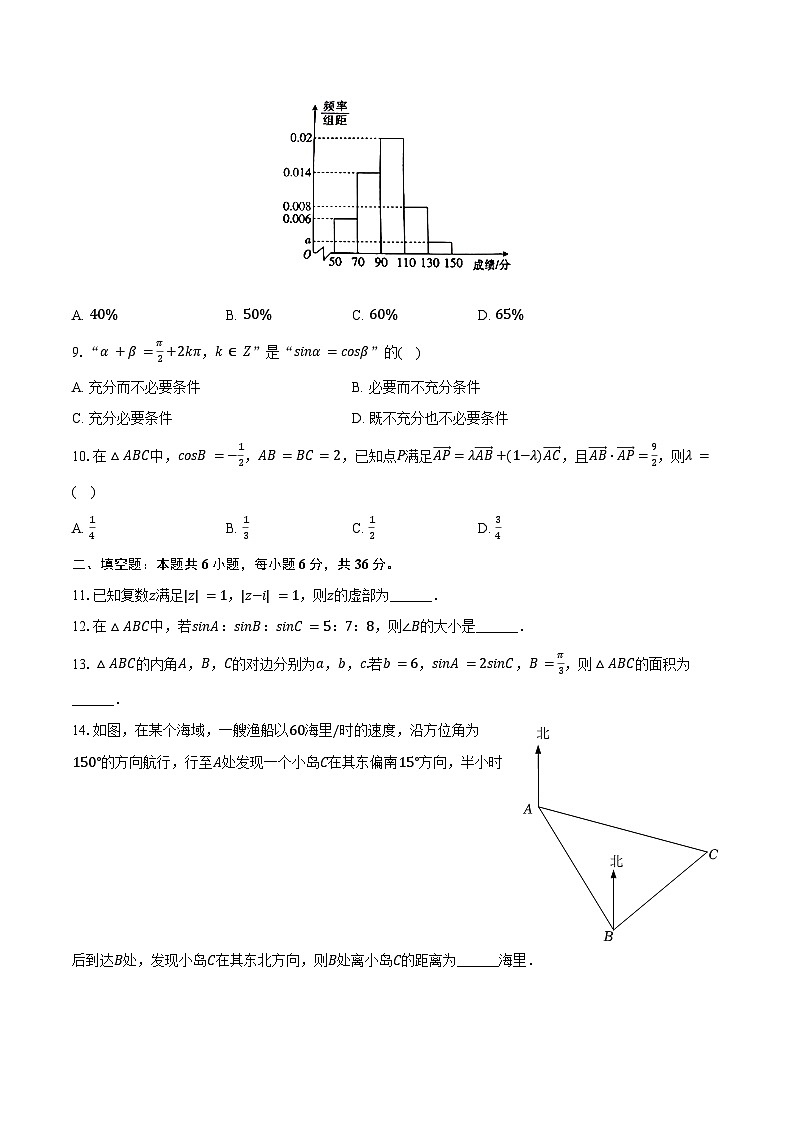
8.为了解某地高三学生的期末语文考试成绩,研究人员随机抽取了100名学生对其进行调查,根据所得数据制成如图所示的频率分布直方图,已知不低于90分为及格,则这100名学生期末语文成绩的及格率为( )
A. 40%B. 50%C. 60%D. 65%
9.“α+β=π2+2kπ,k∈Z”是“sinα=csβ”的( )
A. 充分而不必要条件B. 必要而不充分条件
C. 充分必要条件D. 既不充分也不必要条件
10.在△ABC中,csB=−12,AB=BC=2,已知点P满足AP=λAB+(1−λ)AC,且AB⋅AP=92,则λ=( )
A. 14B. 13C. 12D. 34
二、填空题:本题共6小题,每小题6分,共36分。
11.已知复数z满足|z|=1,|z−i|=1,则z的虚部为______.
12.在△ABC中,若sinA:sinB:sinC=5:7:8,则∠B的大小是______.
13.△ABC的内角A,B,C的对边分别为a,b,c.若b=6,sinA=2sinC,B=π3,则△ABC的面积为______.
14.如图,在某个海域,一艘渔船以60海里/时的速度,沿方位角为150°的方向航行,行至A处发现一个小岛C在其东偏南15°方向,半小时后到达B处,发现小岛C在其东北方向,则B处离小岛C的距离为______海里.
15.边长为2的等边△ABC中,|BD|=1,CE=EA,则AD⋅BE的最小值为______.
16.如果存在函数g(x)=ax+b(a,b为常数),使得对函数f(x)定义域内任意x都有f(x)≤g(x)成立,那么称g(x)为函数f(x)的一个“线性覆盖函数”.给出如下四个结论:
①函数f(x)=2x存在“线性覆盖函数”;
②对于给定的函数f(x),其“线性覆盖函数”可能不存在,也可能有无数个;
③g(x)=12x+12为函数f(x)= x的一个“线性覆盖函数”;
④若g(x)=2x+b为函数f(x)=−x2的一个“线性覆盖函数”,则b>1
其中,所有正确结论的序号是______.
三、解答题:本题共4小题,共64分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题16分)
已知函数f(x)=asinxcsx+cs(2x+π6),且f(π4)=32.
(1)求a的值和f(x)的最小正周期;
(2)求f(x)在[0,π]上的单调递增区间.
18.(本小题16分)
已知A,B,C分别为△ABC三边a,b,c所对的角,向量m=(sinA,sinB),n=(csB,csA),且m⋅n=sin2C.
(1)求角C的大小;
(2)若sinA+sinB=2sinC,且CA⋅(AB−AC)=18,求边c的长.
19.(本小题16分)
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知b=2,sinA+sinBsinB+sinC=ca−2.
(1)求角A.
(2)从以下三个条件中任选一个,求△ABC的面积.
①边BC上的中线AD=1;②sinB=13;③角A的平分线AD=1,点D在线段BC上.
注:如果选择多个条件分别解答,按第一个解答计分.
20.(本小题16分)
对于函数f(x),g(x),若存在实数m,n,使得函数ℎ(x)=mf(x)+ng(x),则称ℎ(x)为f(x),g(x)的“合成函数”.
(1)已知f(x)=x−3,g(x)=3−2x,试判断ℎ(x)=x−6是否为f(x),g(x)的“合成函数”?若是,求实数m,n的值;若不是,说明理由;
(2)已知f(x)=sin(x−π4),g(x)=csx,ℎ(x)为f(x),g(x)的“合成函数”,且m=1,n= 2,若关于x的方程f(x+π4)⋅g(x)+kℎ(x)=0在x∈[0,π2]上有解,求实数k的取值范围;
(3)已知f(x)=x,g(x)=3x,ℎ(x)为f(x),g(x)的“合成函数”(其中m>0,n>0),ℎ(x)的定义域为(0,+∞),当且仅当x=3时,ℎ(x)取得最小值6.若对任意正实数x1,x2,且x1+x2=2,不等式ℎ(x1)+ℎ(x2)≥p恒成立,求实数p的最大值.
参考答案
1.A
2.D
3.A
4.B
5.B
6.D
7.A
8.C
9.A
10.D
11.12
12.π3
13.6 3
14.10 6
15.− 3−3
16.②③
17.解:(1)因为f(π4)=32,所以f(π4)=asinπ4csπ4+cs(π2+π6)=32,
即12a−12=32,解得a=4,
所以f(x)=4sinxcsx+cs(2x+π6)=2sin2x+ 32cs2x−12sin2x
=32sin2x+ 32cs2x= 3sin(2x+π6),
所以f(x)的最小正周期为2π2=π.
(2)由−π2+2kπ≤2x+π6≤π2+2kπ,k∈Z,解得−π3+kπ≤x≤π6+kπ,k∈Z,
所以f(x)的单调递增区间为[−π3+kπ,π6+kπ],k∈Z,
所以f(x)在[0,π]上的单调递增区间为[0,π6],[2π3,π].
18.解:(1)由m=(sinA,sinB),n=(csB,csA),
得m⋅n=sinAcsB+csAsinB=sin(A+B)=sinC,
又m⋅n=sin2C,∴sin2C=2sinCcsC=sinC,
∵0
又CA⋅(AB−AC)=18,∴CA⋅CB=18,即abcsC=18,
∴abcsπ3=12ab=18,得ab=36.
由余弦定理得c= a2+b2−2abcsC= (a+b)2−3ab= 4c2−3×36,
解得c=6.
19.解:(1)由题意sinA+sinBsinB+sinC=ca−2,
由正弦定理可得a+bb+c=ca−2,即a+22+c=ca−2,
则a2−c2=2c+4,
由余弦定理得a2=4+c2−4ccsA,所以a2−c2=4−4ccsA,
所以2c+4=4−4ccsA,所以csA=−12,
又因为0
所以AD=12(AB+AC),即12=14(c2+4−2c),
即c2−2c=0,又因为c>0,所以c=2,
由(1)知csA=−12,所以sinA= 32,
所以S△ABC=12bcsinA=12×2×2× 32= 3;
若选②:当sinB=13,由csA=−12,所以sinA= 32,
由正弦定理:asinA=bsinB,即a 32=213,解得a=3 3,
由(1)可得a2−c2=2c+4,即c2+2c−23=0,
解得:c=2 6−1或c=−1−2 6(舍),
所以S△ABC=12bcsinA=12×2×(2 6−1)× 32=3 2− 32;
若选③:角A的平分线AD=1,则∠DAC=π3,又因为b=2,
在△ADC中由余弦定理可得CD2=b2+AD2−2b⋅ADcs∠DAC=4+1−4csπ3,
所以CD= 3,此时AD2+CD2=AC2,所以∠ADC=π2,所以AD⊥BC,
所以可得△ABC为等腰三角形,所以c=b=2,
所以S△ABC=12×BC×AD=12×2 3×1= 3.
20.解:(1)假设ℎ(x)=x−6为f(x),g(x)的“合成函数”,
则ℎ(x)=x−6=m(x−3)+n(3−2x)=(m−2n)x+3(n−m),
所以m−2n=13(n−m)=−6,解得m=3,n=1,
所以ℎ(x)=x−6为f(x),g(x)的“合成函数”,且m=3,n=1;
(2)因为f(x)=sin(x−π4),且m=1,n= 2,
所以ℎ(x)=sin(x−π4)+ 2csx= 22(sinx+csx),
由f(x+π4)⋅g(x)+kℎ(x)=0,
得sinxcsx+ 22k(sinx+csx)=0(∗),
令t=sinx+csx= 2sin(x+π4),
则t2=(sinx+csx)2=1+2sinxcsx,所以sinxcsx=t2−12,
因为x∈[0,π2],所以x+π4∈[π4,3π4],故t∈[1, 2],
所以方程(∗)为t2−12+ 22kt=0在t∈[1, 2]上有解,
所以 2k=1t−t,
因为函数y=1t,y=−t在t∈[1, 2]上都是减函数,
所以函数y=1t−t在t∈[1, 2]上是减函数,
所以 2k=1t−t∈[ 22− 2,0],
所以k∈[−12,0];
(3)由题意ℎ(x)=mx+3nx,m>0,n>0,x∈(0,+∞),
得ℎ(x)=mx+3nx≥2 3mn,
当且仅当mx=3nx,即x= 3nm时取等号,
所以m>0n>0 3nm=32 3mn=6,解得m=1n=3,
所以ℎ(x)=x+9x,x∈(0,+∞),
则ℎ(x1)+ℎ(x2)=x1+x2+9x1+9x2≥p恒成立,
因为x1+x2=2,所以ℎ(x1)+ℎ(x2)=x1+x2+9x1+9x2=2+18x1x2≥p,
又x1x2≤(x1+x2)24=1,当且仅当x1=x2=1时取等号,
所以ℎ(x1)+ℎ(x2)=2+18x1x2≥20,
所以p≤20,
所以实数p的最大值为20.
[数学]2024~2025学年北京市海淀区中关村中学高二(上)开学试卷(有答案): 这是一份[数学]2024~2025学年北京市海淀区中关村中学高二(上)开学试卷(有答案),共9页。
北京市中关村中学2024-2025学年高二上学期开学调研考试数学试题(解析版): 这是一份北京市中关村中学2024-2025学年高二上学期开学调研考试数学试题(解析版),共16页。试卷主要包含了 复数, 已知,则与夹角为, 已知,,则等于, 若,则“”是“”的, “,”是“”的等内容,欢迎下载使用。
北京市中关村中学2024-2025学年高二上学期开学调研考试数学试题(原卷版): 这是一份北京市中关村中学2024-2025学年高二上学期开学调研考试数学试题(原卷版),共4页。试卷主要包含了 复数, 已知,则与的夹角为, 已知,,则等于, 若,则“”是“”的, “,”是“”的等内容,欢迎下载使用。












