2023-2024学年山东省滨州市惠民县七年级（下）期末数学试卷（含答案）

这是一份2023-2024学年山东省滨州市惠民县七年级（下）期末数学试卷（含答案），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.有下列命题：①两点确定一条直线；②相等的角是直角；③内错角相等；④两点之间，线段最短.其中，假命题的个数是( )
A. 4B. 3C. 2D. 1
2.下列数值是不等式2x+3>9的解的是( )
A. −3B. 0C. 3D. 6
3.下列调查方式，你认为最合适的是( )
A. 旅客上飞机前的安检，采用抽样调查方式
B. 了解端午节到北京旅游的人数，采用抽样调查方式
C. 了解全国中学生的用眼卫生情况，采用全面调查方式
D. 了解一批手机电池的使用寿命，采用全面调查方式
4.一副直角三角板(∠ACB=30°,∠BED=45°)按如图所示的位置摆放，如果AC//DE，那么∠EBC的度数是( )
A. 15°
B. 20°
C. 30°
D. 35°
5.下列数据中不能确定物体位置的是( )
A. 西偏北30°B. 花园小区13号楼701号
C. 孙武路460号D. 东经120°，北纬60°
6.具备下列条件的△ABC中，不是直角三角形的是( )
A. ∠A+∠B=∠CB. ∠A−∠B=∠C
C. ∠A：∠B：∠C=1：2：3D. ∠A=∠B=3∠C
7.如图，已知数轴上的点A，B分别表示数− 2， 2，则下列各数中是无理数且对应的点在线段AB上的是( )
A. 0B. 2−1
C. 3−9D. π
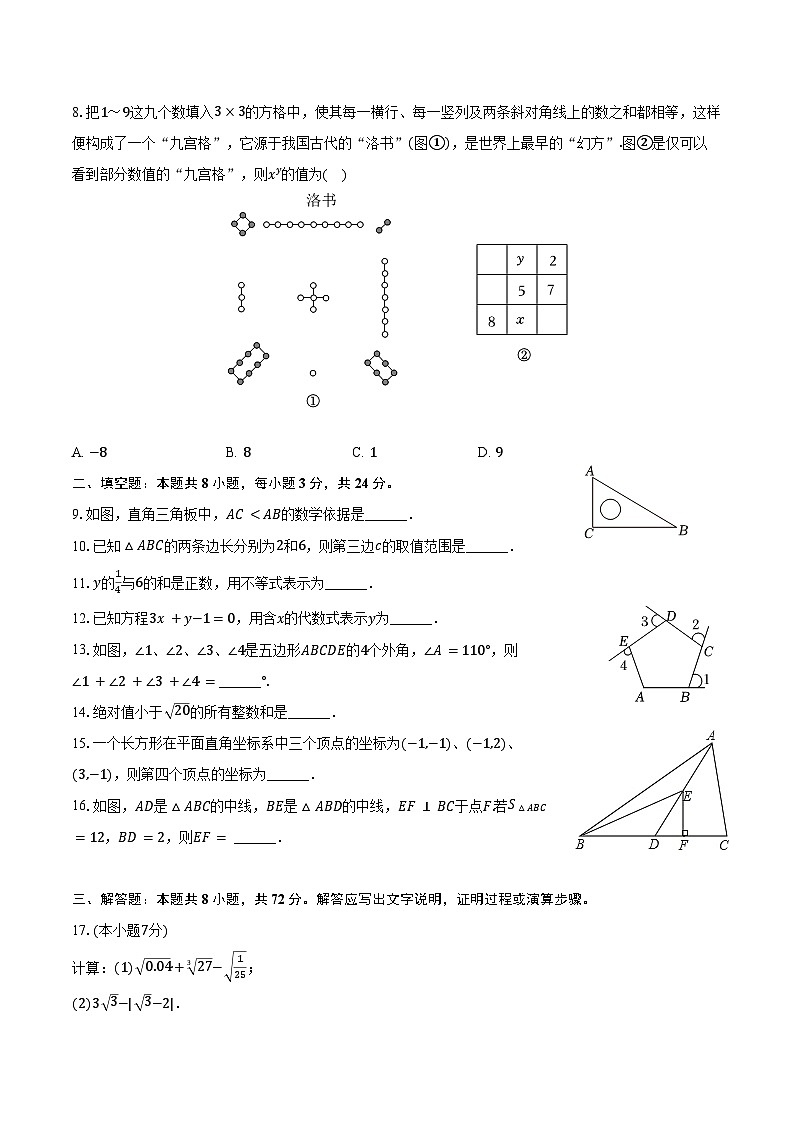
8.把1～9这九个数填入3×3的方格中，使其每一横行、每一竖列及两条斜对角线上的数之和都相等，这样便构成了一个“九宫格”，它源于我国古代的“洛书”(图①)，是世界上最早的“幻方”.图②是仅可以
看到部分数值的“九宫格”，则xy的值为( )
A. −8B. 8C. 1D. 9
二、填空题：本题共8小题，每小题3分，共24分。
9.如图，直角三角板中，AC3(x+1)与12x−1≤7−32x都成立？
19.(本小题9分)
某校为满足学生课外活动的需求，准备开设五类运动项目，分别为A：篮球，B；足球，C；乒乓球，D：羽毛球，E：跳绳.为了解学生的报名情况，现随机抽取八年级部分学生进行调查，并根据调查结果绘制了如下两幅不完整的统计图．
请根据图文信息回答下列问题：
(1)请求出项目C的人数并将条形统计图补充完整；
(2)在此扇形统计图中，项目D所对应的扇形圆心角的大小为______；
(3)若该校共有1500名学生，请你估计全校报篮球的学生人数．
20.(本小题9分)
先画图再解决问题：
(1)如图1，点C是∠AOB的边OB上一点，在图中画出点C到OA的垂线段CD，垂足为点D，再过C点画出OA的平行线CE，根据所画图形写出2对相等的角；
(2)如图2，在正方形网格中，每个小正方形的边长为1，三角形ABC的顶点都在正方形顶点上，将三角形ABC先向左平移2个单位，再向下平移3个单位，得到三角形A′B′C′，请你画出平移后的三角形A′B′C′，则AB与A′B′的关系为______；三角形A′B′C′的面积为______．
21.(本小题10分)
如图，△ABC中，D为BC上一点，∠C=∠BAD，△ABC的角平分线BE交AD于点F．
(1)求证：∠AEF=∠AFE；
(2)G为BC上一点，当FE平分∠AFG且∠C=30°时，求∠CGF的度数．
22.(本小题10分)
应用题：为了丰富学生校园生活，满足学生的多元文化需求，促进学生身心健康和谐发展，学校将要举行趣味运动会，体育组准备购买跳绳作为奖品.已知1条短跳绳和3条长跳绳，共需要96元；2条短跳绳和1条长跳绳共需要62元．
(1)求每条短跳绳和每条长跳绳各多少元；
(2)商店举行“优惠促销”活动，具体办法如下：短跳绳“九折”优惠；长跳绳不超过10条不优惠，超出10条的部分“六折”优惠.如果买m条短跳绳需要y1元，买n条长跳绳需要y2元.请用含m，n的代数式分别表示y1和y2；
(3)如果在(2)的条件下，购买同一种奖品50件，请分析买哪种奖品省钱．
23.(本小题10分)
如图所示的图形，像我们常见的符号——箭号.我们不妨把这样图形叫做“箭头四角形”．
探究：
(1)观察“箭头四角形”，试探究图1中∠BDC与∠A，∠B，∠C之间的关系，并说明理由；
应用：
(2)请你直接利用以上结论，解决以下两个问题：
①如图2，把一块三角尺XYZ放置在△ABC上，使三角尺的两条直角边XY、XZ恰好经过点B，C，若∠A=60°，则∠ABX+∠ACX= ______°；
②如图3，∠ABE，∠ACE的二等分线(即角平分线)BF，CF相交于点F，若∠BAC=60°，∠BEC=130°，求∠BFC的度数．
24.(本小题10分)
【教材回顾】
在人教版七年级下册数学教材第109页的数学活动中，我们探究了“以方程x−y=0的解为坐标(x的值为横坐标，y的值为纵坐标)的点的特性”，了解了二元一次方程的解与其图象上点的坐标的关系．
规定：以方程x−y=0的解为坐标的点的全体叫做方程x−y=0的图象；
结论：一般地，在平面直角坐标系中，任何一个二元一次方程的图象都是一条直线．
【解决问题】
(1)请你在图中所给的平面直角坐标系中画出二元一次方程组2x+y=4,x−y=−1中的两个二元一次方程的图象(提示：依据“两点确定一条直线”，画出图象即可，无需写过程)．
(2)观察图象，两条直线的交点坐标为______，由此你得出这个二元一次方程组的解是______．
【拓展延伸】
已知二元一次方程ax+by=7的图象经过两点A(−1,3)和B(2,1)，试求a，b的值．
参考答案
1.C
2.D
3.B
4.A
5.A
6.D
7.B
8.C
9.垂线段最段
10.43(x+1)得：x>2，
解不等式12x−1≤7−32x得：x≤4，
所以不等式组的解集为23(x−1)与12x−1≤7−32x都成立．
19.(1)调查的总人数为10÷10%=100(人)，
C组的人数为：100−20−30−15−10=25 (人)，
补全条形图如图所示：
(2)项目D所对应的扇形圆心角的大小为360°×15100=54°，
(3)全校报篮球的学生人数为1500×20100=300(人)．
20.(1)图形如图所示，∠ECB=∠O，┐ODC=∠DCE(答案不唯一)；
(2)AB=A′B′，AB//A′B′；7.5．
21.解：(1)证明：∵BE平分∠ABC，
∴∠ABE=∠CBE，
又∵∠C=∠BAD，
∴∠ABF+∠BAD=∠CBE+∠C，
∵∠AFB+∠ABF+∠BAD=180°，∠CEB+∠CBE+∠C=180°，
∴∠AFB=∠CEB
∴∠AEF=∠AFE；
(2)∵FE平分∠AFG，
∴∠AFE=∠GFE，
∵∠AEF=∠AFE，
∴∠AEF=∠GFE，
∴FG//AC，
∵∠C=30°，
∴∠CGF=180°−∠C=150°．
22.解：(1)设每条短跳绳的售价为a元，每条长跳绳的售价为b元，
依题意得：a+3b=962a+b=62，
解得：a=18b=26．
答：每条短跳绳的售价为18元，每条长跳绳的售价为26元．
(2)依题意得：y1=18×0.9m=16.2m；
当010时，y2=26×10+0.6×26(n−10)=15.6n+104．
∴y2=26n(010,且n为整数)．
(3)当m=50时，y1=16.2×50=810；
当n=50时，y2=15.6×50+104=884．
∵810