+辽宁省丹东市第五中学2023-2024学年八年级上学期入学数学试卷+

这是一份+辽宁省丹东市第五中学2023-2024学年八年级上学期入学数学试卷+，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.体育精神就是健康向上、不懈奋斗的精神，下列关于体育运动的图标中是轴对称图形的是( )
A. B. C. D.
2.下列运算不正确的是( )
A. B. C. D.
3.下列成语所反映的事件中，是不可能事件的是( )
A. 十拿九稳B. 守株待兔C. 水中捞月D. 一箭双雕
4.如图，，，并且，则的度数为( )
A.
B.
C.
D.
5.如图分割的正方形，拼接成长方形的方案中，可以验证( )
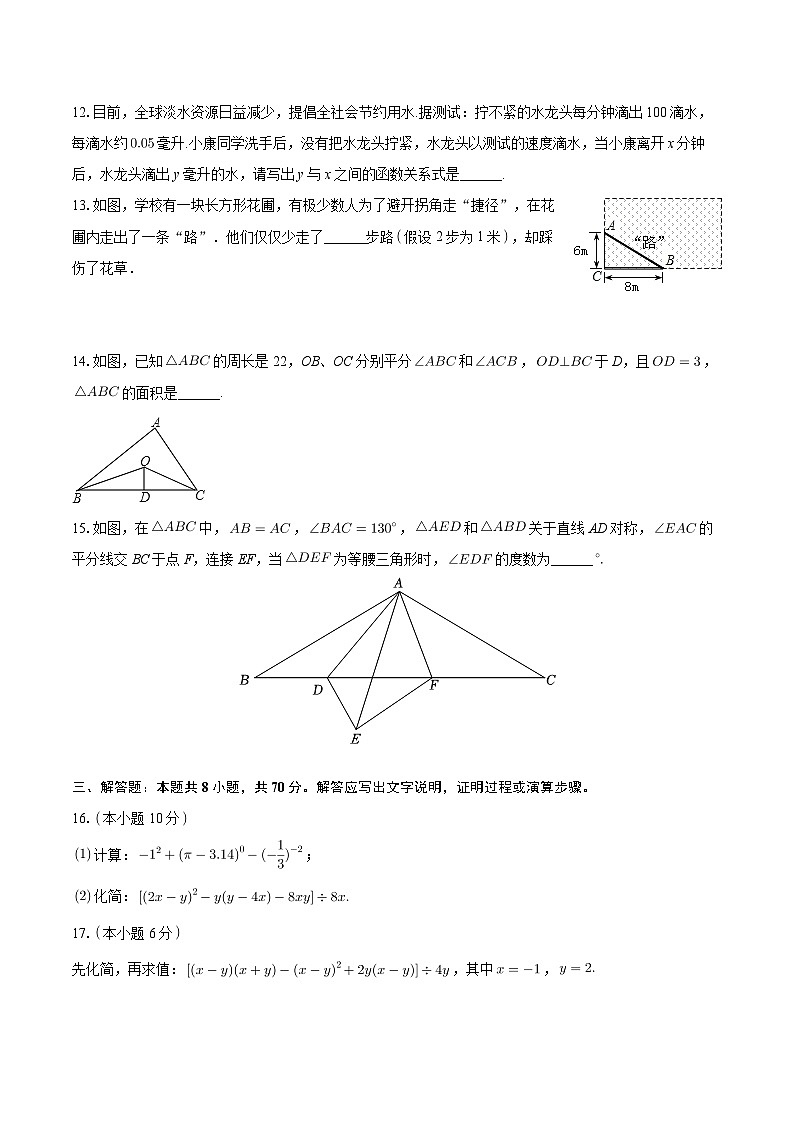
A. B.
C. D.
6.如图，已知和中，，下列条件不能说明≌的是( )
A.
B.
C.
D.
7.如图，在中，已知点D、E、F分别是BC、AD、CE的中点，且的面积为32，则的面积是( )
A. 2B. 4C. 6D. 8
8.若x是256的算术平方根，则x的算术平方根是( )
A. B. 16C. D. 4
9.如图，一条笔直的河L，牧马人从P地出发，到河边M处饮马，然后到Q地，现有如下四种方案，可使牧马人所走路径最短的是( )
A. B.
C. D.
10.如图，在中，，AD平分，，BD：：2，则点D到AB的距离为( )
A. 18
B. 12
C. 15
D. 不能确定
二、填空题：本题共5小题，每小题2分，共10分。
11.清代诗人袁枚的一首诗《苔》中写到：“白日不到处，青春恰自来.苔花如米小，也学牡丹开.”苔花的花粉直径约为米，用科学记数法表示为______米.
12.目前，全球淡水资源日益减少，提倡全社会节约用水.据测试：拧不紧的水龙头每分钟滴出100滴水，每滴水约毫升.小康同学洗手后，没有把水龙头拧紧，水龙头以测试的速度滴水，当小康离开x分钟后，水龙头滴出y毫升的水，请写出y与x之间的函数关系式是______.
13.如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．他们仅仅少走了______步路假设2步为1米，却踩伤了花草．
14.如图，已知的周长是22，OB、OC分别平分和，于D，且，的面积是______.
15.如图，在中，，，和关于直线AD对称，的平分线交BC于点F，连接EF，当为等腰三角形时，的度数为______
三、解答题：本题共8小题，共70分。解答应写出文字说明，证明过程或演算步骤。
16.本小题10分
计算：；
化简：
17.本小题6分
先化简，再求值：，其中，
18.本小题8分
如图所示的是一个正六边形转盘被分成6个全等的等边三角形，指针位置固定，转动转盘后任其自由停止，其中的某个三角形会恰好停在指针所指的位置，并相应得到一个数当指针指向两个三角形的公共边时，需重新转动转盘，这时称转动了转盘1次.
下列说法正确的是______直接填空；
A.出现的数为3的概率小于出现的数为4的概率
B.转动转盘，出现的数为6是随机事件
C.转动转盘6次，2一定会出现一次
D.转动转盘3次，出现的3个数之和有可能等于19
求转动一次转盘，指针指向偶数的概率.
19.本小题8分
如图，在中，
尺规作图：作边AB的垂直平分线，交AB于点D，交AC于点E；保留作图痕迹，不要求写作法
连接BE，若，，求的周长．
20.本小题8分
按逻辑将下面的证明过程补充完整.
如图，点E、F分别在AB、CD上，于点O，，
求证：请填空.
证明：______，
______
____________
已知，
______
已知，
____________
______
21.本小题8分
甲骑摩托车从A地去B地，乙开汽车从B地去A地，同时出发，匀速行驶，各自到达终点后停止，甲、乙两人之间的距离为与甲行驶的时间之间的关系如图所示.
观测图象可知点M、点N、点P所代表的实际意义，请将M、N、P分别填入对应的横线上.
①点______表示甲到达终点；
②点______表示甲乙两人相遇；
③点______表示乙到达终点.
、B两地之间的路程为______千米；
求甲骑摩托车的速度；
甲出发______ h后，甲、乙两人相距180千米.
22.本小题10分
我国著名数学家曾说：“数无形时少直觉，形少数时难入微.”数形结合思想是解决问题的有效途径，请阅读材料完成下面问题：
【算法赏析】
若x满足，求的值.
解：设，，
则，
；
【算法体验】
若x满足，求的值；
【算法应用】
如图，已知数轴上点A，B，C表示的数分别是m，10，以AB为边作正方形ABDE，以AC为边作正方形ACFG，延长ED交FC于点若正方形ACFG的面积与正方形ABDE的面积的和为119，请直接写出长方形ACPE的面积.
23.本小题12分
【问题初探】
在数学活动课上，李老师给出如下问题：如图1，中，点D，E在边BC上，，过D作交AE于点F，判断AE是否平分？请说明理由.
下面是两位同学的做法：
如图2，小美同学从线段FE的角度去考虑，倍长FE，使，连接CG；
如图3，小丽同学从线段AE的角度去考虑，倍长AE，使，连接DG；
请你选择一名同学的解题思路，写出证明过程.
【类比分析】
如图4，在中，，CE是的中线，请判断BC与CE的数量关系，并说明理由.
【学以致用】
如图5，在中，分别以AB，AC为直角边向内作等腰直角三角形，，，，AD是BC边上的中线，已知，求EF的长.
答案和解析
1.【答案】C
【解析】解：不是轴对称图形，故此选项不符合题意；
B.不是轴对称图形，故此选项不符合题意；
C.是轴对称图形，故此选项符合题意；
D.不是轴对称图形，故此选项不符合题意．
故选：
根据轴对称图形的概念求解．
本题考查了轴对称图形，关键是掌握好轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2.【答案】D
【解析】解：，故选项A正确，不符合题意；
，故选项B正确，不符合题意；
，故选项C正确，不符合题意；
，故选项D错误，符合题意；
故选：
计算出各个选项中式子的正确结果，即可判断哪个选项符合题意．
本题考查整式的混合运算，熟练掌握运算法则是解答本题的关键．
3.【答案】C
【解析】解：A、十拿九稳是随时事件，不符合题意；
B、守株待兔是随机事件，不符合题意；
C、水中捞月是不可能事件，符合题意；
D、一箭双雕是随机事件，不符合题意；
故选：
根据随机事件的定义对各选项进行逐一分析即可．
本题考查随机事件，熟练掌握随机事件的概念是解题的关键．
4.【答案】A
【解析】解：如图延长AC交DE于点
，
，
，
，
故选
延长AC交DE于点根据即可解决问题．
本题考查平行线的性质、三角形的外角的性质，解题的关键是添加辅助线，利用三角形的外角等于不相邻的两个内角和解决问题，属于中考常考题型．
5.【答案】A
【解析】解：如图，
图1的面积可表示为，
图2阴影部分面积可表示为，
可以验证，
故选：
图1的面积可表示为，图2阴影部分面积可表示为，即可求解．
本题考查了图形面积的求法，平方差公式的几何背景，解题关键是数形结合的解题思想．
6.【答案】A
【解析】【分析】
本题考查了全等三角形的判定定理，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS，两直角三角形全等还有根据全等三角形的判定定理逐个判断即可．
【解答】
解：，，，不符合全等三角形的判定定理，不能推出≌，故本选项符合题意；
B.，，，符合全等三角形的判定定理AAS，能推出≌，故本选项不符合题意；
C.，，，符合全等三角形的判定定理ASA，能推出≌，故本选项不符合题意；
D.，，，符合全等三角形的判定定理SAS，能推出≌，故本选项不符合题意；
故选：
7.【答案】D
【解析】解：是BC的中点，
，
是AD的中点，
，
，
是CE的中点，
，
故选：
根据三角形中线平分三角形面积先求出，进而求出，，则，同理即可得到
本题主要考查了三角形的面积，熟知三角形的中线把三角形分成面积相等的两部分是解题关键．
8.【答案】D
【解析】解：根据题意得：，
则x的算术平方根为
故选：
利用算术平方根的定义计算得到x的值，求出x的算术平方根即可．
此题考查了算术平方根，熟练掌握平方根的定义是解本题的关键．
9.【答案】D
【解析】解：使牧马人所走路径最短的是，
故选：
根据轴对称得出最短路径即可．
此题考查轴对称问题，此题为数学知识的应用，关键是利用的知识点为两点之间线段最短．
10.【答案】B
【解析】解：：：2，，
故选：
由已知条件开始思考，结合角平分线的性质，得点D到AB的距离即为CD长．
本题主要考查平分线的性质；由已知能够注意到D到AB的距离等于CD长是解决问题的关键．
11.【答案】
【解析】解：，
故答案为：
科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值时，n是正数；当原数的绝对值时，n是负数．
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，n为整数，表示时关键要正确确定a的值以及n的值．
12.【答案】
【解析】解：由题意得：，
即
故答案为：
每分钟滴出100滴水，每滴水约毫升，则一分钟滴水毫升毫升，则x分钟可滴5x毫升，据此即可求解．
本题主要考查了根据实际问题列一次函数解析式，正确表示出一分钟滴的水的体积是解题的关键．
13.【答案】8
【解析】【分析】
此题主要考查了勾股定理的应用，正确应用勾股定理是解题关键．
直接利用勾股定理得出AB的长，再利用进而得出答案．
【解答】解：由题意可得：，
则，
故他们仅仅少走了：步
故答案为
14.【答案】33
【解析】【分析】
根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC的距离都相等，从而可得到的面积等于周长的一半乘以OD，然后列式进行计算即可求解．本题考查了角平分线上的点到角的两边的距离相等的性质，判断出三角形的面积与周长的关系是解题的关键．
【解答】
解：如图，连接OA，
、OC分别平分和，
点O到AB、AC、BC的距离都相等，
的周长是22，于D，且，
故答案为
15.【答案】50或65或80
【解析】解：，，
令，
和关于直线AD对称，
，，
，且AF平分，
，，
同理可得，
，
当时，
，
当时，
当时，
综上所述，的度数为：或或
故答案为：50或65或
令，根据轴对称的性质及三角形的外角定理用m表示出三个内角的度数，再对等腰进行分类讨论即可解决问题．
本题主要考查了轴对称的性质及等腰三角形的性质，熟知轴对称的性质及对等腰三角形那进行分类讨论是解题的关键．
16.【答案】解：原式
；
原式

【解析】根据实数的运算法则计算即可；
根据整式的混合运算法则计算即可．
本题考查的是整式的混合运算，实数的运算，熟练掌握上述知识点是解题的关键．
17.【答案】解：原式
，
当，时，
原式

【解析】根据整式的加减运算法则进行化简，然后将x与y的值代入原式即可求出答案．
本题考查整式的混合运算，解题的关键是熟练运用整式的加减运算法则，本题属于基础题型．
18.【答案】B
【解析】解：、出现的数为3的概率与出现的数为4的概率均为，此结论错误；
B、转动转盘，出现的数为6是随机事件，此结论正确；
C、转动转盘6次，2不一定会出现，此结论错误；
D、转动转盘3次，
出现的3个数之和最大是18，不可能等于19，此结论错误．
故选：B；
个数中，偶数有3个，
指针指向偶数的概率为
直接利用随机事件的意义分析得出即可；
根据概率公式求解可得．
本题主要考查了概率的意义与概率公式，用到的知识点为：概率=所求情况数与总情况数之比．
19.【答案】解：如图，DE为所作；
垂直平分AB，
，
，，
的周长
【解析】利用基本作图作AB的垂直平分线即可；
先利用线段垂直平分线的性质得到，然后利用等线段代换得到的周长
本题考查了作图-基本作图：熟练掌握5种基本作图是解决问题的关键．也考查了线段垂直平分线的性质和等腰三角形的性质．
20.【答案】已知 垂直的定义 直角三角形的两锐角互余 同角的余角相等 等量代换 内错角相等，两直线平行
【解析】证明：已知，
垂直的定义，
直角三角形的两锐角互余
已知，
同角的余角相等
已知，
等量代换
内错角相等，两直线平行
故答案为：已知；垂直的定义；；直角三角形的两锐角互余；同角的余角相等；；等量代换；内错角相等，两直线平行．
根据垂直的定义求出，根据直角三角形的两锐角互余求出，同角的余角相等及等量代换求出，再根据“内错角相等，两直线平行”即可得证．
此题考查了平行线的判定与性质，熟练运用平行线的判定定理与性质定理是解题的关键．
21.【答案】或
【解析】解：分析函数图象知出发2小时时，甲乙在途中相遇；出发3小时时乙到达A地；6小时时甲到达B地．
故答案为：①P；②M；③N；
根据函数图象和图象中的数据可以解答本题．由图象可得，AB两地之间路程为240千米，
故答案为：240；
甲的速度是：千米/时，
答：甲骑摩托车的速度为40千米/时；
①相遇之前：小时，
②相遇之后：小时，
故答案为：或
根据函数图象和图象中的数据可以解答本题．由图象可得，AB两地之间路程为240千米；出发2小时时，甲乙在途中相遇；出发3小时时乙到达A地；6小时时甲到达B地．据此解答．
本题考查一次函数的应用，解答本题的关键是明确题意，找出所求问题需要的条件，利用函数的思想和数形结合的思想解答．
22.【答案】解：设，，
，
，
，
；
设，，
，
正方形ACFG的面积与正方形ABDE的面积的和为119，
，
，
，
长方形ACPE的面积

【解析】设，，则，，然后利用完全平方公式进行计算即可解答；
设，，则，，然后利用完全平方公式进行计算即可解答．
本题考查了整式的混合运算-化简求值，完全平方公式的几何背景，准确熟练地进行计算是解题的关键．
23.【答案】解：小美同学的解题思路，证明：延长FE至G，使，连接
在和中，
，
≌，
，，
，
，
，
，
，
，
，
平分；
小丽同学的解题思路，证明：延长AE至G，使，连接DG，
在和中，
，
≌
，
，
，
，
，
，
，
，
平分；
，
理由：延长CE到F，使，连接DF，
是的中线，
，
，
≌，
，，
，
，
，，
，
，
，
≌，
，
，
；
解：延长AD至G，使，连接BG，如图5所示：
是BC边上的中线，
，
在和中，
，
≌，
，，
，
，
，
，
，
，
，
在和中，
，
≌，
，
，

【解析】小美同学的解题思路，延长FE至G，使，连接根据全等三角形的性质得到，，求得，得到，根据平行线的性质得到，根据角平分线的定义得到AE平分；
小丽同学的解题思路，延长AE至G，使，连接DG，根据全等三角形的性质的，得到，求得，根据平行线的性质得到，根据角平分线的定义得到AE平分；
延长CE到F，使，连接DF，根据全等三角形的性质得到，，求得，推出，根据全等三角形的性质即可得到结论；
延长AD至G，使，连接BG，如图5所示：根据全等三角形的性质得到，，根据平行线的性质得到，求得，根据全等三角形的性质即可得到结论．
本题是三角形综合题目，考查了全等三角形的判定与性质、等腰直角三角形的性质、平行线的判定与性质以及角平分线的判定等知识；本题综合性强，熟练掌握等腰直角三角形的性质，证明三角形全等是解题的关键，属于中考常考题型．