初中北师大版（2024）2 平行线分线段成比例教案

这是一份初中北师大版（2024）2 平行线分线段成比例教案，共6页。
1.理解并掌握基本事实“两条直线被一组平行线所截,所得的对应线段成比例”及其推论.
2.进一步体会由特殊到一般的归纳推理的思想和方法.
学习重点
平行线分线段成比例定理和推论及其应用.
学习难点
平行线分线段成比例定理及推论的灵活应用,平行线分线段成比例定理的变式.
课时活动设计
复习回顾
1.什么是成比例线段?
2.你能不通过测量快速将一根绳子分成两部分,使得这两部分的比是2∶3吗?
设计意图:复习成比例线段的内容,回顾通过方格纸探究成比例线段性质的过程.通过生活中实例的引入激发学生探究的欲望.
探求新知一
如图1,小方格的边长均内1,直线l1∥l2∥l3,分别交直线m,n于格点A1,A2,A3,B1,B2,B3.
(1)计算A1A2A2A3与B1B2B2B3,A1A2A1A3与B1B2B1B3,A2A3A1A3与B2B3B1B3的值,你有什么发现?
(2)将l2向下平移到如图2的位置,直线m,n与直线l2的交点分别为A2,B2.你在问题(1)中发现的结论还成立吗?如果将l2平移到其他位置呢?
(3)在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗?
分组合作,学生在组内互相交流讨论,组内达成共识后展示讨论结果,教师给予指导并进行归纳总结.
得出结论:
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例.
议一议:
(1)如何理解“对应线段”?
(2)平行线分线段成比例定理的几何语言如何表示?
解:(1)如图,若a∥b∥c,则A1A2A2A3=B1B2B2B3.
(2)∵a∥b∥c,
∴A1A2A2A3=B1B2B2B3上下=上下,A1A2A1A3=B1B2B1B3上全=上全,
A2A3A1A3=B2B3B1B3下全=下全.
设计意图:让学生在探究得出结论的基础上,对平行线分线段成比例定理有进一步的理解,并掌握定理的几何语言,进一步发展推理能力.
探求新知二
1.如图1,直线a∥b∥c,分别交直线m,n于点A1,A2,A3,B1,B2,B3.将直线n向左平移,使点B1与点A1重合,点B2,B3的位置记为点C2,C3.
(1)图2中有哪些成比例线段?
图1 图2 图3
(2)如图3,在△ABC中,D,E分别是边AB和AC上的点,且DE∥BC,图5中有哪些成比例线段?
学生独立完成后尝试总结归纳,教师多媒体展示.
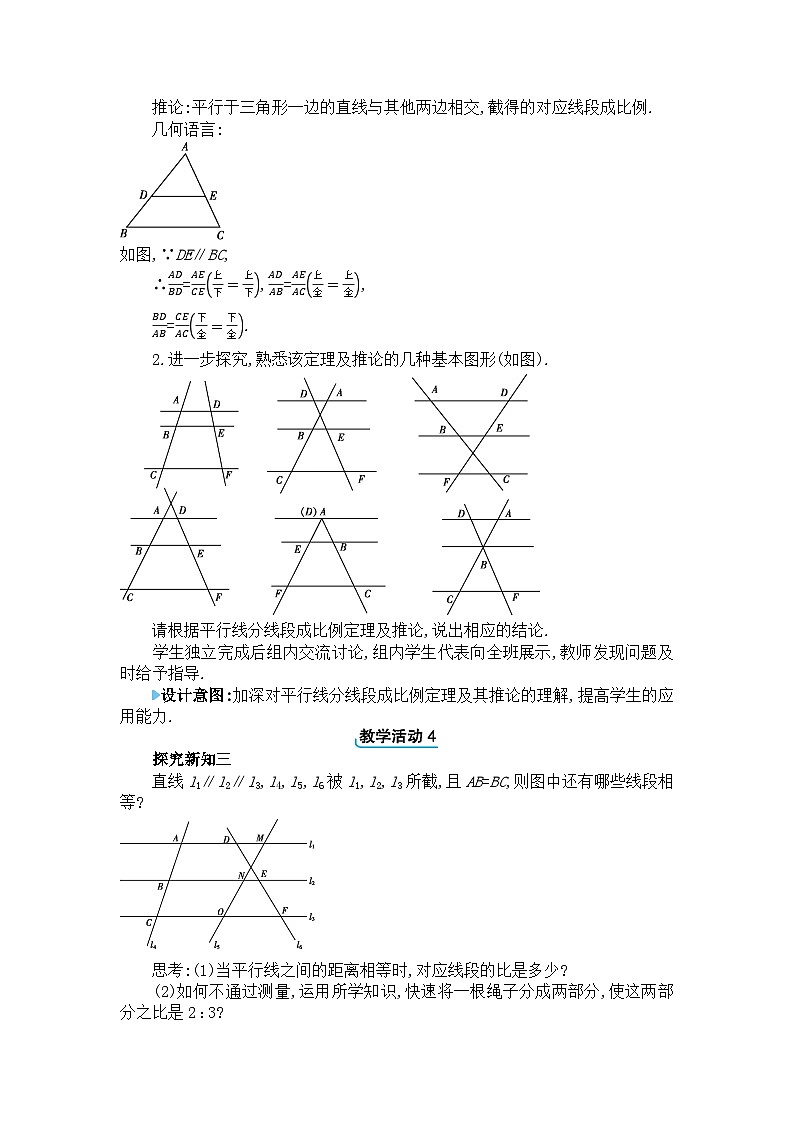
推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
几何语言:
如图,∵DE∥BC,
∴ADBD=AECE上下=上下,ADAB=AEAC上全=上全,
BDAB=CEAC下全=下全.
2.进一步探究,熟悉该定理及推论的几种基本图形(如图).
请根据平行线分线段成比例定理及推论,说出相应的结论.
学生独立完成后组内交流讨论,组内学生代表向全班展示,教师发现问题及时给予指导.
设计意图:加深对平行线分线段成比例定理及其推论的理解,提高学生的应用能力.
探究新知三
直线l1∥l2∥l3,l4,l5,l6被l1,l2,l3所截,且AB=BC,则图中还有哪些线段相等?
思考:(1)当平行线之间的距离相等时,对应线段的比是多少?
(2)如何不通过测量,运用所学知识,快速将一根绳子分成两部分,使这两部分之比是2∶3?
设计意图:与导入问题相呼应,通过有层次的问题,学生独立解决课堂导入中的问题2,加深对平行线分线段成比例定理的理解,同时激发学生学习的兴趣.
巩固训练
1.如图,在△ABC中,点E,F分别是AB和AC上的点,且EF∥BC.
(1)如果AE=7,EB=5,FC=4,那么AF的长是多少?
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
解:(1)∵EF∥BC,
∴AFCF=AEBE.
∵AE=7,EB=5,FC=4,
∴AF4=75.
∴AF=285.
(2)∵EF∥BC,
∴FCAC=BEAB.
即FCAF+FC=AB-AEAB.
∵AB=10,AE=6,AF=5,
∴FC5+FC=10-610.
∴FC=103.
2.如图,在△ABC中,D,E分别是AB和AC上的点,且DE∥BC.
(1)如果AD=3.2 cm,DB=1.2 cm,AE=2.4 cm,那么EC的长是多少?
(2)如果AB=5 cm,AD=3 cm,AC=4 cm,那么EC的长是多少?
解:(1)∵DE∥BC,
∴ECAE=DBAD.
∵AD=3.2 cm,DB=1.2 cm,AE=2.4 cm,
∴EC2.4=
∴EC=0.9 cm.
(2)∵DE∥BC,
∴ECAC=BDAB.
即ECAC=AB-ADAB.
∵AB=5 cm,AD=3 cm,AC=4 cm,
∴EC4=5-35.
∴EC=85.
设计意图:通过对平行线分线段成比例定理的简单应用,培养学生严谨的逻辑推理能力,加深对知识的理解.
课堂小结
本节课你有哪些收获?
1.两条直线被一组平行线所截,所得的对应线段成比例.
2.平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
设计意图:师生通过反思评价,对知识和方法进行总结,巩固平行线分线段成比例定理及其推论.
课堂8分钟.
1.课本第84~85页习题4.3第1,3,4题.
2.七彩作业.
4.2 平行线分线段成比例
平行线分线段成比例定理:两条直线被一组平行线所截,所得的对应线段成比例.
推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.
基本图形:
教学反思