山东省烟台市经开区2023-2024学年八年级下学期期末考试数学试卷（五四制）

这是一份山东省烟台市经开区2023-2024学年八年级下学期期末考试数学试卷（五四制），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.下列根式中，属于最简二次根式的是( )
A. B. C. D.
2.一元二次方程用直接开平方法可转化为两个一元一次方程，其中一个一元一次方程是，则另一个一元一次方程是( )
A. B. C. D.
3.对于反比例函数，下列说法正确的是( )
A. 图象经过点
B. 若点和点在该图象上，则
C. 其图象既是轴对称图形又是中心对称图形
D. y随x的增大而增大
4.关于x的一元二次方程有两个不相等的实数根，则m满足( )
A. B. 且C. 且D.
5.若与可以合并成一项，则n可以为( )
A. 6B. 12C. 15D. 45
6.下列运算正确的是( )
A. B.
C. D.
7.已知，那么下列四个选项一定正确的是( )
A. B. C. D.
8.用公式法解方程：，其中判别式的值是( )
A. 56B. 16C. 4D. 8
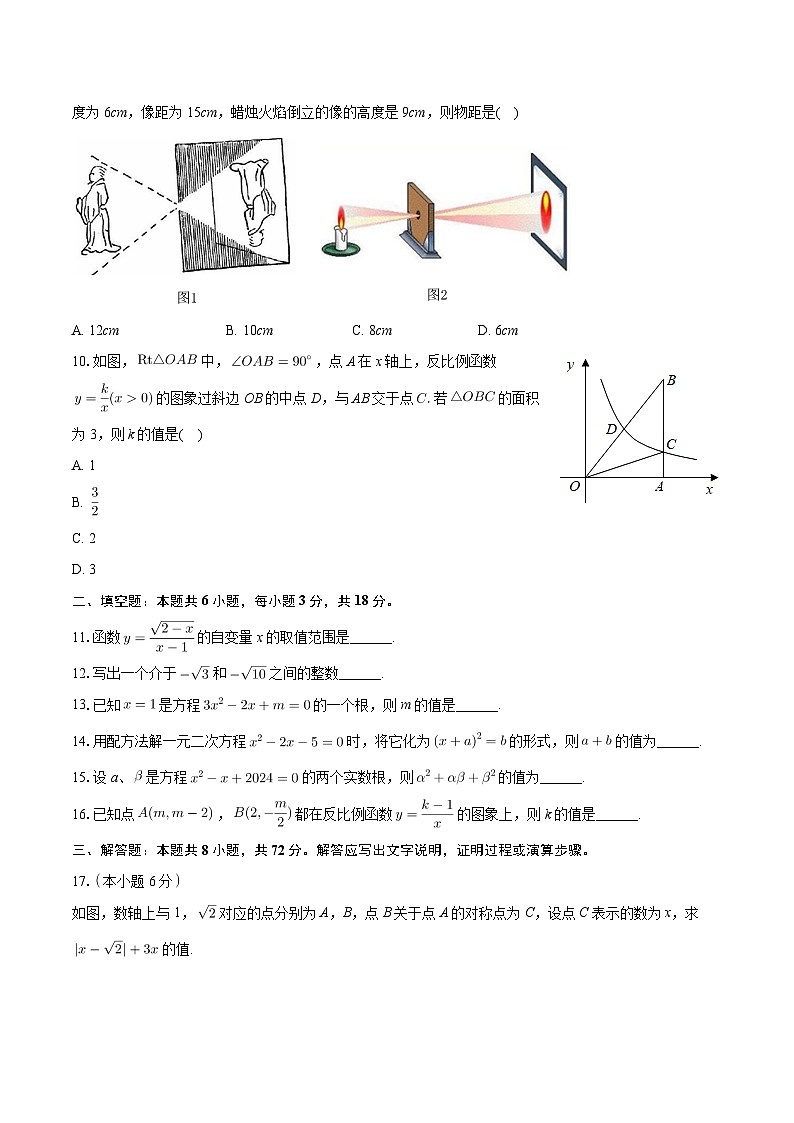
9.大约在两千四五百年前，如图1墨子和他的学生做了世界上第1个小孔成倒像的实验.并在《墨经》中有这样的精彩记录：“景到，在午有端，与景长，说在端”.如图2所示的小孔成像实验中，若蜡烛火焰的高度为6cm，像距为15cm，蜡烛火焰倒立的像的高度是9cm，则物距是( )
A. 12cmB. 10cmC. 8cmD. 6cm
10.如图，中，，点A在x轴上，反比例函数的图象过斜边OB的中点D，与AB交于点若的面积为3，则k的值是( )
A. 1
B.
C. 2
D. 3
二、填空题：本题共6小题，每小题3分，共18分。
11.函数的自变量x的取值范围是______.
12.写出一个介于和之间的整数______.
13.已知是方程的一个根，则m的值是______.
14.用配方法解一元二次方程时，将它化为的形式，则的值为______.
15.设a、是方程的两个实数根，则的值为______.
16.已知点，都在反比例函数的图象上，则k的值是______.
三、解答题：本题共8小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.本小题6分
如图，数轴上与1，对应的点分别为A，B，点B关于点A的对称点为C，设点C表示的数为x，求的值.
18.本小题7分
已知关于x的一元二次方程的两个实数根是和，且，求m的值.
19.本小题8分
如图，小亮同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与树顶B在同一直线上．已知纸板的两条边，，延长DF交AB于点C，测得边DF离地面的高度，，求树高
20.本小题8分
已知关于x的方程有两个不相等的实数根.
求n的取值范围；
若n为符合条件的最小整数，且该方程的较大根是较小根的3倍，求m的值.
21.本小题10分
2024年龙年春晚吉祥物形象“龙辰辰”正式发布亮相，作为中华民族重要的精神象征和文化符号，千百年来，龙的形象贯穿文学、艺术、民俗、服饰、绘画等各个领域，也呈现了吉祥如意、平安幸福的美好寓意.现某商店推出销售吉祥物活动，已知吉祥物每件的进货价为30元，经市场调研发现，当该吉祥物的销售单价为40元时，每天可销售300件；当销售单价每增加2元，每天的销售数量将减少10件销售利润=销售总额-进货成本
若“龙辰辰”吉祥物的销售单价为46元，则当天销售量为______件；
该吉祥物的当天利润有可能达到6200元吗？若能，请求出此时的销售单价；若不能，请说明理由.
22.本小题10分
如图，在x轴的正半轴上依次截取，过点，，，…，分别作x轴的垂线与反比例函数的图象相交于点，，…，连接，，，…，分别与，，，…，交于点，，，…，得，四边形，四边形，四边形，…，并设其面积分别为，，，…，以此类推.
求；
直接写出及的值.
23.本小题11分
问题背景：一次数学综合实践活动课上，小慧发现并证明了关于三角形角平分线的一个结论.如图①，已知AD是的角平分线，可证小慧的证明思路是：如图②，过点C作，CE交AD的延长线于点E，构造相似三角形来证明尝试证明：
请参照小慧提供的思路，利用图②证明：
应用拓展：
如图③，在中，，D是边BC上一点.连接AD，将沿AD所在直线折叠，点C恰好落在边AB上的E点处.若，，求DE的长.
24.本小题12分
如图，中，，，点，点，反比例函数的图象经过点
求反比例函数的解析式；
将直线OA向上平移m个单位后经过反比例函数图象上的点，求m，n的值.
答案和解析
1.【答案】D
【解析】解：A、，故不符合题意，
B、，故不符合题意，
C、，故不符合题意，
D、属于最简二次根式，故符合题意；
故选：
根据最简二次根式的定义，逐一判断即可解答．
本题考查了最简二次根式、二次根式的性质与化简，熟练掌握最简二次根式的定义是解题的关键．
2.【答案】C
【解析】解：，
，
或，
故选：
根据直接开平方法可以解答本题．
本题考查解一元二次方程，解答本题的关键是明确解方程的方法．
3.【答案】C
【解析】解：，
图象经过点不合题意；
B.，，故不合题意；
C.图象既是轴对称图形又是中心对称图形，符合题意；
D.在每一象限内，y随x的增大而增大，故不合题意．
故选：
依据反比例函数的图象与性质逐一判定即可．
本题考查了反比例函数的图象与性质，熟记性质是解题的关键．
4.【答案】B
【解析】解：方程有两个不相等的实数根，
，
解得：且
故选：
根据根的判别式结合二次项系数非0，即可得出关于m的一元一次不等式组，解不等式组即可得出m的取值范围．
本题考查了根的判别式，根据根的判别式结合二次项系数非0列出关于m的一元一次不等式组是解题的关键．
5.【答案】D
【解析】解：与可以合并成一项，
与是同类二次根式，
当时，与不是同类二次根式，A选项不符合题意；
当时，与不是同类二次根式，B选项不符合题意；
当时，与不是同类二次根式，C选项不符合题意；
当时，与是同类二次根式，D选项符合题意；
故选：
把每个选项的n的值代入二次根式，化简后，再确定与是不是同类二次根式，从而可得答案．
本题考查的是合并同类项，同类二次根式的识别，掌握同类二次根式的含义是解题的关键．
6.【答案】B
【解析】解：A、不是同类二次根式，不能合并，故选项错误；
B、，故选项正确；
C、应等于，故选项错误；
D、应该等于，故选项错误；
故选：
A、B、C、D利用根式的运算顺序及运算法则、公式等计算即可求解．
本题考查的是二次根式的运算能力．注意：要正确掌握运算顺序及运算法则、公式等．
7.【答案】C
【解析】解：，
，，
，，
，
无法得到
故选：
利用比例的性质对各选项进行判断．
本题考查了比的性质，熟练掌握比例的性质是解决此题的关键．
8.【答案】A
【解析】解：原方程可化为，
，，，
故选：
先得出a，b，c的值，再求出的值即可．
本题主要考查的是根的判别式，熟知是解题的关键．
9.【答案】B
【解析】解：设物距是x cm，
由相似三角形的性质得到：
解得
即物距是
故选：
直接利用相似三角形的对应边成比例解答．
本题考查相似三角形的判定与性质的实际应用及分析问题、解决问题的能力．利用数学知识解决实际问题是中学数学的重要内容．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．
10.【答案】C
【解析】解：过点D作于点E，则，
是OB的中点，
，
，，
，
，
∽，
，
，
，
又，
，
故选：
根据反比例函数系数k的几何意义可得，由中点的定义和相似三角形的性质可得，再根据，可求出答案．
本题考查反比例函数系数k的几何意义，相似三角形的判定和性质，理解反比例函数系数k的几何意义以及相似三角形的性质是解决问题的关键．
11.【答案】且
【解析】解：根据二次根式的意义可知：，即，
根据分式的意义可知：，即，
且
根据二次根式和分式有意义的条件，被开方数大于等于0，分母不等于0，就可以求解．
主要考查了函数自变量的取值范围的确定和分式的意义．函数自变量的范围一般从三个方面考虑：
当函数表达式是整式时，自变量可取全体实数；
当函数表达式是分式时，考虑分式的分母不能为0；
当函数表达式是二次根式时，被开方数为非负数．
12.【答案】
【解析】解：，
介于和之间的整数为：，
故答案为：答案不唯一
根据无理数比较大小可得结果．
本题考查估算无理数的大小，解题的关键是熟练掌握估算无理数大小的方法，此题答案不唯一，符合题意即可．
13.【答案】
【解析】解：把代入得，
解得
故答案为
根据一元二次方程的解，把代入方程得到关于m的一次方程，然后解此一次方程即可．
本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．
14.【答案】5
【解析】解：，
，
，
，
，，
，
故答案为：
根据配方法的步骤：①把常数项移到等号的右边；②等式两边同时加上一次项系数一半的平方，把左边配成一个完全平方式，右边化为一个常数项，由此可得出a，b的值，即可得出答案．
本题考查解一元二次方程-配方法，能够将一元二次方程正确配方是解答本题的关键．
15.【答案】
【解析】解：，是方程的两个实数根，
，，
故答案为：
根据根与系数的关系可以求出，，将可化为，代入求值即可解答．
本题考查的是一元二次方程根与系数的关系，利用两根之和与两根之积进行计算与转化是解决问题的关键．
16.【答案】0
【解析】解：点，都在反比例函数的图象上，
，
整理得：，
解得：，舍去，
，
；
故答案为：
由于两点在同一函数图象上，则两点横纵坐标之积等于比例系数，据此列出方程组即可解答．
本题考查了反比例函数图象上点的坐标特征，所有在反比例函数上的点的横纵坐标的积应等于比例系数．
17.【答案】解：，B两点表示的数分别为1，，
点所表示的数是，
根据绝对值的意义进行化简：
原式

【解析】首先根据已知条件可以确定线段AB的长度，然后根据对称的性质即可确定x的值，代入所求代数式计算即可解决问题．
此题主要考查了实数与数轴之间的对应关系，解题时要求能够熟练计算数轴上两点间的距离；根据绝对值的性质进行化简去掉绝对值及掌握分母有理化的方法．
18.【答案】解：由题意知，，，
，
，
，
整理得，
解得，
经检验，是方程的解，
的值为或
【解析】根据根与系数的关系知，，由进行变形直接代入得到，求解可得．
本题考查了一元二次方程根与系数的关系：若，是一元二次方程的两根时，，
19.【答案】解：，，
，，
∽，
，
即，
解得，
树高
【解析】根据相似三角形的性质得到，据此可得BC的长，再根据线段的和差即可得到结论．
本题考查了相似三角形的应用和勾股定理的应用，解题的关键是证得∽
20.【答案】解：关于x的方程有两个不相等的实数根，
，
；
为符合条件的最小整数，，
，
原方程为：，
设该方程的根是a，3a，
，，
解得，或，不合题意，舍去，
的值为
【解析】根据一元二次方程的根的判别式，建立关于n的不等式，求出n的取值范围；
由题意可得，设该方程的根是a，3a，根据根与系数的关系列方程求解即可．
本题考查了一元二次方程根的判别式和根与系数的关系，熟知一元二次方程的根的判别式和根与系数的关系是解题的关键．
21.【答案】270
【解析】解：根据题意得：
件，
若“龙辰辰”吉祥物的销售单价为46元，则当天销售量为270件．
故答案为：270；
该吉祥物的当天利润不能达到6200元，理由如下：
假设该吉祥物的当天利润能达到6200元，设销售单价增加x元，则每件的销售利润为元，每天可销售件，
根据题意得：，
整理得：，
，
原方程没有实数根，
假设不成立，即该吉祥物的当天利润不能达到6200元．
利用当天的销售量，即可求出结论；
假设该吉祥物的当天利润能达到6200元，设销售单价增加x元，则每件的销售利润为元，每天可销售件，利用总利润=每件的销售利润每天的销售量，可列出关于x的一元二次方程，由根的判别式，可得出原方程没有实数根，进而可得出假设不成立，即该吉祥物的当天利润不能达到6200元．
本题考查了一元二次方程的应用、根的判别式以及有理数的混合运算，解题的关键是：根据各数量之间的关系，列式计算；找准等量关系，正确列出一元二次方程．
22.【答案】解：、在反比例函数图象上，
，
，
∽，
，
：：2，
，
，
，
，
，
，
同理，
同理
同理，

【解析】可证∽，利用相似三角形性质得到，再利用求出即可；
根据的计算方法求出、即可．
本题考查了反比例函数k值的几何意义、反比例函数图象上点的坐标特征、图形的变化规律，熟练掌握相似三角形的判定与性质是关键．
23.【答案】证明：，
，，
∽，
，
，，
，
，
解：将沿AD所在直线折叠，点C恰好落在边AB上的E点处，
，，
由可知，，
又，，
，
，
，
，
，
，
；

【解析】证明∽，由相似三角形的性质得出，证出，则可得出结论；
由折叠的性质可得出，，由可知，，由勾股定理求出，则可求出答案．
本题是相似形综合题，考查了折叠的性质，角平分线的定义，等腰三角形的判定与性质，平行线的性质，相似三角形的判定与性质，勾股定理，熟练掌握相似三角形的判定与性质是解题的关键．
24.【答案】解：过A作轴于D，如图：
，
，
在和中，
，
≌，
，，
，，
，，
，
反比例函数的图象经过点A，
，解得，
反比例函数的解析式为；
由得，
设直线OA解析式为，
则，解得，
直线OA解析式为，
将直线OA向上平移m个单位后所得直线解析式为，
点在反比例函数图象上，
，
直线OA向上平移m个单位后经过的点是，
，
综上所述，，
【解析】过A作轴于D，证明≌，可得，，根据，，得，而反比例函数的图象经过点A，故，解得，即可得反比例函数的解析式为；
求出直线OA解析式为，可得将直线OA向上平移m个单位后所得直线解析式为，再由点在反比例函数图象上，得，即直线OA向上平移m个单位后经过的点是，即可求出
本题考查一次函数与反比例函数的综合应用，涉及三角形全等的判定及性质，解题的关键是由≌得到，及待定系数法的运用．