2024年黑龙江省哈尔滨市69中学数学九年级第一学期开学监测试题【含答案】

这是一份2024年黑龙江省哈尔滨市69中学数学九年级第一学期开学监测试题【含答案】，共24页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）一蓄水池有水40m3,按一定的速度放水，水池里的水量y (m3)与放水时间t(分)有如下关系：
下列结论中正确的是
A．y随t的增加而增大B．放水时间为15分钟时，水池中水量为8m3
C．每分钟的放水量是2m3D．y与t之间的关系式为y=38-2t
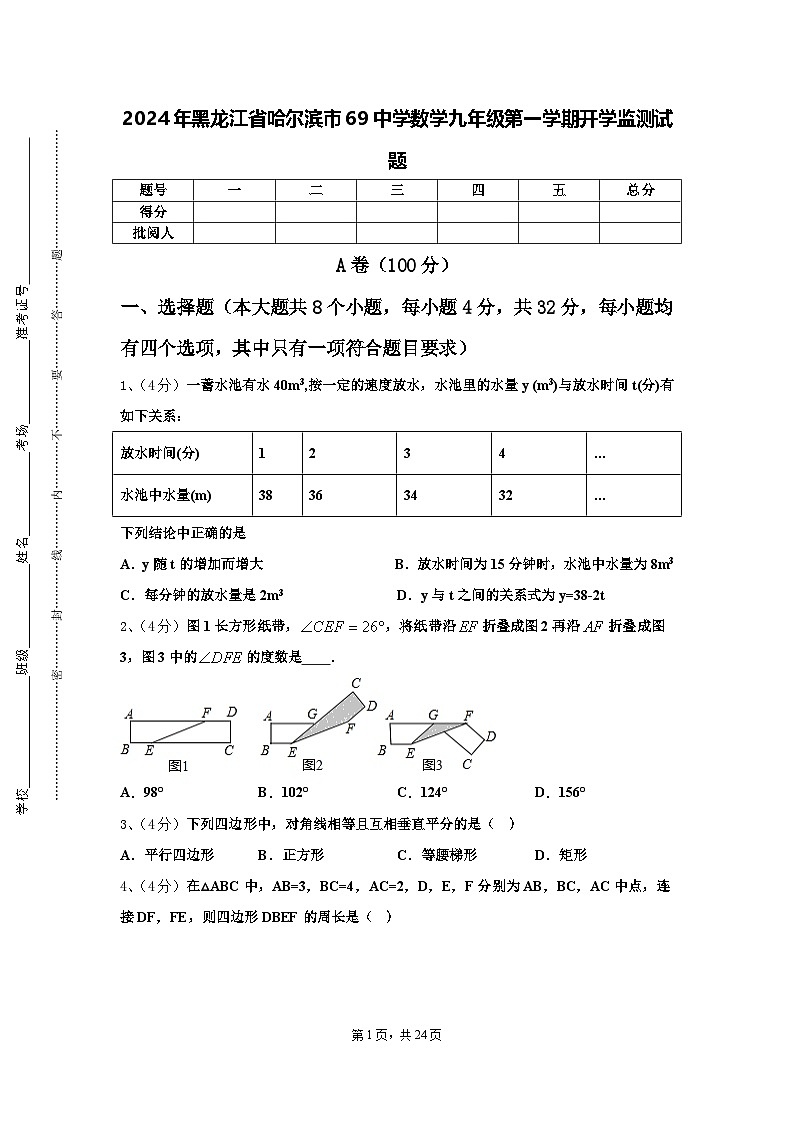
2、（4分）图1长方形纸带，，将纸带沿折叠成图2再沿折叠成图3，图3中的的度数是 ．
A．98°B．102°C．124°D．156°
3、（4分）下列四边形中，对角线相等且互相垂直平分的是（ ）
A．平行四边形B．正方形C．等腰梯形D．矩形
4、（4分）在△ABC中，AB=3，BC=4，AC=2，D，E，F分别为AB，BC，AC中点，连接DF，FE，则四边形DBEF的周长是（ ）
A．5B．7C．9D．11
5、（4分）下列交通标志中、既是轴对称图形又是中心对称图形的是（ ）
A．B．C．D．
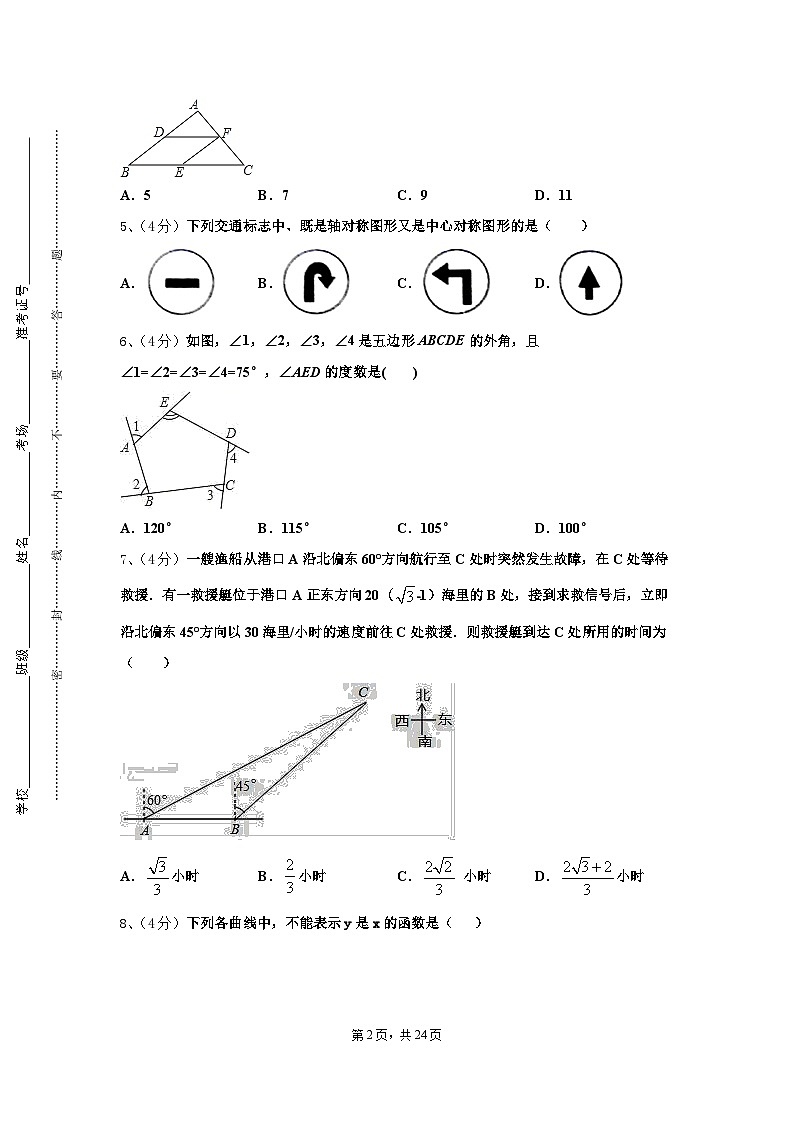
6、（4分）如图，∠1，∠2，∠3，∠4是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=75°，∠AED的度数是( )
A．120°B．115°C．105°D．100°
7、（4分）一艘渔船从港口A沿北偏东60°方向航行至C处时突然发生故障，在C处等待救援．有一救援艇位于港口A正东方向20（﹣1）海里的B处，接到求救信号后，立即沿北偏东45°方向以30海里/小时的速度前往C处救援．则救援艇到达C处所用的时间为（ ）
A．小时B．小时C． 小时D．小时
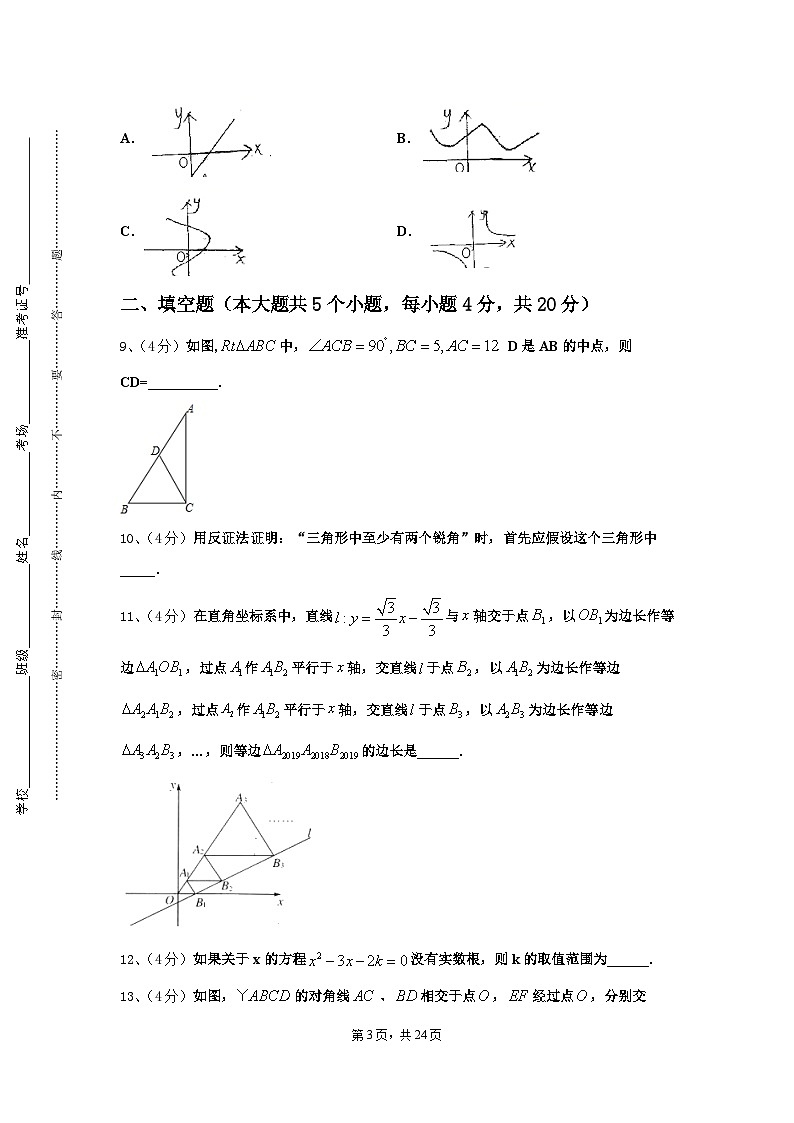
8、（4分）下列各曲线中，不能表示y是x的函数是（ ）
A．B．
C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）如图,中， D是AB的中点，则CD=__________.
10、（4分）用反证法证明：“三角形中至少有两个锐角”时，首先应假设这个三角形中_____．
11、（4分）在直角坐标系中，直线与轴交于点，以为边长作等边，过点作平行于轴，交直线于点，以为边长作等边，过点作平行于轴，交直线于点，以为边长作等边，…，则等边的边长是______.
12、（4分）如果关于x的方程没有实数根，则k的取值范围为______.
13、（4分）如图，的对角线、相交于点，经过点，分别交、于点、，已知的面积是，则图中阴影部分的面积是_____.
三、解答题（本大题共5个小题，共48分）
14、（12分）定向越野作为一种新兴的运动项目，深受人们的喜爱. 这种定向运动是利用地图和指北针到访地图上所指示的各个点标，以最短时间按序到达所有点标者为胜. 下面是我区某校进行定向越野活动中，中年男子组的成绩（单位：分:秒）.
9:01 14:45 9:46 19:22 11:20 18:47 11:40 12:32 11:52 13:45
22:27 15:00 17:30 13:22 18:34 10:45 19:24 16:26 21:33 15:31
19:50 14:27 15:55 16:07 20:43 12:13 21:41 14:57 11:39 12:45
12:57 15:31 13:20 14:50 14:57 9:41 12:13 14:27 12:25 12:38
例如，用时最少的赵老师的成绩为9:01，表示赵老师的成绩为9分1秒.
以下是根据某校进行定向越野活动中，中年男子组的成绩中的数据，绘制的统计图表的一部分．
某校中年男子定向越野成绩分段统计表
（1）这组数据的极差是____________；
（2）上表中的a =____________ ,b =____________ , c =____________, d =____________；
（3）补全频数分布直方图.
15、（8分）某车行经销的A型自行车去年6月份销售总额为1.6万元，今年由于改造升级每辆车售价比去年增加200元，今年6月份与去年同期相比，销售数量相同，销售总额增加25%．
今年A，B两种型号车的进价和售价如下表：
（1）求今年A型车每辆售价多少元？
（2）该车行计划7月份用不超过4.3万元的资金新进一批A型车和B型车共50辆，应如何进货才能使这批车售完后获利最多？
16、（8分） (﹣)2(+)+|2﹣|﹣
17、（10分）已知，如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交与BE的延长线于点F，且AF=DC，连结CF．
（1）求证：四边形ADCF是平行四边形；
（2）当AB与AC有何数量关系时，四边形ADCF为矩形，请说明理由．
18、（10分）一组数据：1，1，2，5，x的平均数是1．
(1)求x的值；
(2)求这组数据的方差．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）已知一次函数y=kx+b的图像过点（-1,0）和点（0,2），则该一次函数的解析式是______。
20、（4分）化成最简二次根式后与最简二次根式的被开方数相同，则a的值为______.
21、（4分）如图,点P是等边三角形ABC内一点,且PA=3,PB=4, PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数______．
22、（4分）一个多边形截去一个角后，形成新多边形的内角和为2520°，则原多边形边数为_____．
23、（4分）如图，直线y=mx与双曲线y=交于A、B两点，D为x轴上一点，连接BD交y轴与点C，若C（0，-2）恰好为BD中点，且△ABD的面积为6，则B点坐标为__________.
二、解答题（本大题共3个小题，共30分）
24、（8分）电话计费问题，下表中有两种移动电话计费方式：
温馨揭示：方式一：月使用费固定收（月收费：38元/月）；主叫不超限定时间不再收费（80分钟以内，包括80分钟）；主叫超时部分加收超时费（超过部分0.15元/）；被叫免费。
方式二：月使用费0元（无月租费）；主叫限定时间0分钟；主叫每分钟0.35元/；被叫免费。
（1）设一个月内用移动电话主叫时间为，方式一计费元，方式二计费元。写出和关于的函数关系式。
（2）在平面直角坐标系中画出（1）中的两个函数图象，记两函数图象交点为点，则点的坐标为_____________________（直接写出坐标，并在图中标出点）。
（3）根据（2）中函数图象，请直接写出如何根据每月主叫时间选择省钱的计费方式。
25、（10分）如图，在四边形ABCD中，AB∥CD，∠BCD=90°，AB=AD=10cm，BC=8cm，点P从点A出发，以每秒2cm的速度沿线段AB向点B方向运动，点Q从点D出发，以每秒3cm的速度沿线段DC向点C运动，已知动点P、Q同时出发，点P到达B点或点Q到达C点时，P、Q运动停止，设运动时间为t (秒)．
（1）求CD的长；
（2）当四边形PBQD为平行四边形时，求t的值；
（3）在点P、点Q的运动过程中，是否存在某一时刻，使得PQ⊥AB？若存在，请求出t的值并说明理由；若不存在，请说明理

26、（12分）先化简，再求值：，其中.
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、C
【解析】
根据表格内的数据，利用待定系数法求出y与t之间的函数关系式，由此可得出D选项错误；由-2＜0可得出y随t的增大而减小，A选项错误；代入t=15求出y值，由此可得出：放水时间为15分钟时，水池中水量为10m3，B选项错误；由k=-2可得出每分钟的放水量是2m3，C选项正确．综上即可得出结论．
【详解】
解：设y与t之间的函数关系式为y=kt+b，
将（1，38）、（2，36）代入y=kt+b，
，解得：
∴y与t之间的函数关系式为y=-2t+40，D选项错误；
∵-2＜0，
∴y随t的增大而减小，A选项错误；
当t=15时，y=-2×15+40=10，
∴放水时间为15分钟时，水池中水量为10m3，B选项错误；
∵k=-2，
∴每分钟的放水量是2m3，C选项正确．
故选：C．
本题考查一次函数的应用，利用待定系数法求出函数关系式是解题的关键．
2、B
【解析】
由矩形的性质可知AD∥BC，由此可得出∠AFE=∠CEF=26°，再根据翻折的性质可知每翻折一次减少一个∠AFE的度数，由此即可算出∠DFE度数．
【详解】
解：∵四边形ABCD为长方形，
∴AD∥BC，
∴∠AFE=∠CEF=26°．
由翻折的性质可知：
图2中，∠EFD=180°-∠AFE=154°，∠AFD=∠EFD-∠AFE=128°，
图3中，∠DFE=∠AFD-∠AFE=102°，
故选择：B.
本题考查了翻折变换以及矩形的性质，解题的关键是找出∠DFE=180°-3∠AFE．解决该题型题目时，根据翻折变换找出相等的边角关系是关键．
3、B
【解析】
解：对角线相等且互相垂直平分的四边形是正方形，
故选B．
本题考查等腰梯形的性质；平行四边形的性质；矩形的性质；正方形的性质．
4、B
【解析】
试题解析：∵D、E、F分别为AB、BC、AC中点，∴DF=BC=2，DF∥BC，EF=AB=，EF∥AB，∴四边形DBEF为平行四边形，∴四边形DBEF的周长=2（DF+EF）=2×（2+）=1．故选B．
5、A
【解析】
根据中心对称图形和轴对称图形的概念对各选项分析判断即可得解．
【详解】
A、既是轴对称图形又是中心对称图形，故本选项正确；
B、不是轴对称图形，也不是中心对称图形，故本选项错误；
C、不是轴对称图形，也不是中心对称图形，故本选项错误；
D、是轴对称图形，不是中心对称图形，故本选项错误．
故选：A．
本题考查了轴对称图形和中心对称图形的识别，熟练掌握轴对称图形和中心对称图形的定义是解答本题的关键. 在平面内，一个图形经过中心对称能与原来的图形重合，这个图形叫做叫做中心对称图形；一个图形的一部分，以某条直线为对称轴，经过轴对称能与图形的另一部分重合，这样的图形叫做轴对称图形.
6、A
【解析】
如解图所示,根据多边形的外角和即可求出∠5，然后根据平角的定义即可求出结论．
【详解】
解：∵∠1=∠2=∠3=∠4=75°，
∴∠5=360°﹣75°×4=360°﹣300°=60°，
∴∠AED=180°﹣∠5=180°﹣60°=120°．
故选：A．
此题考查的是多边形的外角和平角的定义，掌握多边形的外角和都等于360°是解决此题的关键．
7、C
【解析】
过点C作CD垂直AB延长线于D，根据题意得∠CDB=45°，∠CAD=30°，设BD=x则CD=BD=x，BC=x，由∠CAD=30°可知tan∠CAD= 即 ，解方程求出BD的长，从而可知BC的长，进而求出救援艇到达C处所用的时间即可.
【详解】
如图：过点C作CD垂直AB延长线于D，则∠CDB=45°，∠CAD=30°，
∵∠CDB=45°，CD⊥BD，
∴BD=CD，
设BD=x，救援艇到达C处所用的时间为t，
∵tan∠CAD=，AD=AB+BD，
∴，得x=20（海里），
∴BC=BD=20（海里），
∴t= = （小时），
故选C.
本题考查特殊角三角函数，正确添加辅助线、熟练掌握特殊角的三角函数值是解题关键.
8、C
【解析】
根据函数是一一对应的关系，给自变量一个值，有且只有一个函数值与其对应，就是函数，如果不是，则不是函数．
【详解】
解：A、满足对于x的每一个取值，y都有唯一确定的值与之对应关系，故A不符合题意；
B、满足对于x的每一个取值，y都有唯一确定的值与之对应关系，故B不符合题意；
C、满足对于x的每一个取值，y有两个值与之对应关系，故C符合题意；
D、满足对于x的每一个取值，y都有唯一确定的值与之对应关系，故D不符合题意；
故选C．
本题主要考查函数的自变量与函数值是一一对应的，即给自变量一个值，有唯一的一个值与它对应．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、6.1
【解析】
首先根据勾股定理求得AB=13，然后由“斜边上的中线等于斜边的一半”来求CD的长度．
【详解】
∵Rt△ABC中，，
∴AB===13，
∵D为AB的中点，
∴CD=AB=6.1．
故答案为：6.1．
本题考查了勾股定理和直角三角形斜边上的中线．在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．
10、三角形三个内角中最多有一个锐角
【解析】
“至少有两个”的反面为“最多有一个”，据此直接写出逆命题即可．
【详解】
∵至少有两个”的反面为“最多有一个”，而反证法的假设即原命题的逆命题正确；
∴应假设：三角形三个内角中最多有一个锐角．
故答案为：三角形三个内角中最多有一个锐角
本题考查了反证法，注意逆命题的与原命题的关系．
11、
【解析】
先从特殊得到一般探究规律后，利用规律解决问题即可；
【详解】
∵直线l：y=x-与x轴交于点B1
∴B1（1，0），OB1=1，△OA1B1的边长为1；
∵直线y=x-与x轴的夹角为30°，∠A1B1O=60°，
∴∠A1B1B2=90°，
∵∠A1B2B1=30°，
∴A1B2=2A1B1=2，△A2B3A3的边长是2，
同法可得：A2B3=4，△A2B3A3的边长是22；
由此可得，△AnBn+1An+1的边长是2n，
∴△A2018B2019A2019的边长是1．
故答案为1．
考查了一次函数图象上点的坐标特征以及等边三角形的性质的运用，解决问题的关键是依据等边三角形的性质找出规律，求得△AnBn+1An+1的边长是2n．
12、
【解析】
根据判别式的意义得到△=（-3）2-4×（-2k）＜0，然后解不等式即可．
【详解】
根据题意得△=（-3）2-4×（-2k）＜0，解得.故答案为.
本题考查根的判别式和解不等式，解题的关键是掌握根的判别式和解不等式.
13、
【解析】
只要证明，可得，即可解决问题.
【详解】
四边形是平行四边形，
，，
，
，
，
.
故答案为：.
本题考查平行四边形的性质。全等三角形的判定和性质等知识，解题的关键是学会用转化的思想思考问题，属于中考常考题型.
三、解答题（本大题共5个小题，共48分）
14、见解析
【解析】
（1）先找出这组成绩的最大值与最小值，计算即可得；
（2）根据分组“9≤x＜11”的频数与频率可求得a的值，然后用a乘0.275可求得b的值，用6除以a可得d，把所有频率相加可求得c，据此填空即可；
（3）根据b的值补全图形即可.
【详解】
（1）这组数据的最大值为22:27，最小值为9:01，
所以极差为：22：27-9：01=13：26，
故答案为：13:26或 13分26秒；
（2）a=4÷0.1=40，b=40×0.275=11，d=6÷40=0.15，
c=0.1+0.275+0.225+0.15+0.075+0.1+0.075=1，
故答案为：40，11，1，0.15.
（3）如图所示.
本题考查了极差、频数分布表、频数分布直方图，熟练掌握频数、频率与总数间的关系是解题的关键.
15、（1）型车每辆售价为1000元；（2）型车30辆、型车20辆，获利最多．
【解析】
（1）设今年型车每辆售价为元，则去年型车每辆售价为元，根据数量总价单价结合今年6月份与去年同期相比销售数量相同，即可得出关于的分式方程，解之经检验后即可得出结论；
（2）设购进型车辆，则购进型车辆，根据总价单价数量结合总费用不超过4.3万元，即可得出关于的一元一次不等式，解之即可得出的取值范围，再根据销售利润单辆利润购进数量即可得出销售利润关于的函数关系式，利用一次函数的性质解决最值问题即可．
【详解】
解：（1）设今年型车每辆售价为元，则去年型车每辆售价为元，
根据题意得：，
解得：，
经检验，是原分式方程的解．
答：今年型车每辆售价为1000元．
（2）设购进型车辆，则购进型车辆，
根据题意得：，
解得：．
销售利润为，
，
当时，销售利润最多．
答：当购进型车30辆、购进型车20辆时，才能使这批车售完后获利最多．
本题考查了分式方程的应用、一次函数的最值以及一元一次不等式的应用，解题的关键是：（1）找准等量关系，正确列出分式方程；（2）根据数量关系，找出销售利润关于的函数关系式．
16、﹣1．
【解析】
首先利用平方差公式化简，进而利用二次根式混合运算法则计算得出答案.
【详解】
原式＝(5﹣3)(﹣)+1﹣1﹣
＝1﹣1+1﹣1﹣
＝﹣1．
此题主要考查了二次根式的混合运算，正确化简二次根式是解题关键．
17、（1）证明见解析，（2）当AB=AC时，四边形ADCF为矩形，理由见解析．
【解析】
（1）可证△AFE≌△DBE，得出AF=BD，进而根据AF=DC，得出D是BC中点的结论；
（2）若AB=AC，则△ABC是等腰三角形，根据等腰三角形三线合一的性质知AD⊥BC；而AF与DC平行且相等，故四边形ADCF是平行四边形，又AD⊥BC，则四边形ADCF是矩形．
【详解】
解：（1）证明：∵E是AD的中点，
∴AE=DE．
∵AF∥BC，
∴∠FAE=∠BDE，∠AFE=∠DBE．
在△AFE和△DBE中，，
∴△AFE≌△DBE（AAS）．
∴AF=BD．
∵AF=DC，
∴BD=DC．
即：D是BC的中点．
（2）AB=AC，理由如下：
∵AF=DC，AF∥DC，
∴四边形ADCF是平行四边形．
∵AB=AC，BD=DC，
∴AD⊥BC即∠ADC=90°．
∴平行四边形ADCF是矩形．
考点：全等三角形的判定与性质；矩形的判定．
18、（1）x=4；（2）2.
【解析】
（1）根据算术平均数定义列出关于x的方程，解之可得x的值；
（2）根据方差计算公式计算可得．
【详解】
解：（1）根据题意知=1，
解得：x=4；
（2）方差为×[（1﹣1）2+（1﹣1）2+（2﹣1）2+（5﹣1）2+（4﹣1）2]=2．
考查方差的定义：一般地设n个数据，x1，x2，…xn的平均数为，则方差S2= ，它反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、y=2x+2
【解析】
根据一次函数解析式y=kx+b，再将点（-1,0）和点（0,2）代入可得方程组，解出即可得到k和b的值，即得到解析式.
【详解】
因为点（-1,0）和点（0,2）经过一次函数解析式y=kx+b，所以0=-x+b，2=b，得到k=2，b=2，所以一次函数解析式是：y=2x+2，故本题答案是：y=2x+2.
本题考查用待定系数法求一次函数解析式，难度不大，关键是掌握待定系数发的运用.
20、1.
【解析】
先将化成最简二次根式，然后根据同类二次根式得到被开方数相同可得出关于a的方程，解出即可．
【详解】
∵与最简二次根式是同类二次根式，且＝1，
∴a+1=3，解得：a=1．
故答案为1．
本题考查了同类二次根式的定义：化成最简二次根式后，被开方数相同，这样的二次根式叫做同类二次根式．
21、150°
【解析】
首先证明△BPQ为等边三角形，得∠BQP=60°，由△ABP≌CBQ可得QC=PA，在△PQC中，已知三边，用勾股定理逆定理证出得出∠PQC=90°，可求∠BQC的度数，由此即可解决问题．
【详解】
解：连接PQ，
由题意可知△ABP≌△CBQ
则QB=PB=4，PA=QC=3，∠ABP=∠CBQ，
∵△ABC是等边三角形，
∴∠ABC=∠ABP+∠PBC=60°，
∴∠PBQ=∠CBQ+∠PBC=60°，
∴△BPQ为等边三角形，
∴PQ=PB=BQ=4，
又∵PQ=4，PC=5，QC=3，
∴PQ2+QC2=PC2，
∴∠PQC=90°，
∵△BPQ为等边三角形，
∴∠BQP=60°，
∴∠BQC=∠BQP+∠PQC=150°
∴∠APB=∠BQC=150°
本题考查旋转的性质、等边三角形的判定和性质、勾股定理的逆定理等知识，解题的关键是勾股定理逆定理的应用，属于中考常考题型．
22、15或16或1
【解析】
试题分析：根据多边形的内角和公式先求出新多边形的边数，然后再根据截去一个角的情况进行讨论．设新多边形的边数为n，则（n﹣2）•180°=2520°，解得n=16，①若截去一个角后边数增加1，则原多边形边数为1，②若截去一个角后边数不变，则原多边形边数为16，③若截去一个角后边数减少1，则原多边形边数为15，故原多边形的边数可以为15，16或1．
故答案为15，16或1．
考点：多边形内角和与外角和．
23、（，-4）
【解析】
设点B坐标为(a，b)，由点C（0，-2）是BD中点可得b=-4，D（-a，0），根据反比例函数的对称性质可得A（-a，4），根据A、D两点坐标可得AD⊥x轴，根据△ABD的面积公式列方程可求出a值，即可得点B坐标.
【详解】
设点B坐标为(a，b)，
∵点C（0，-2）是BD中点，点D在x轴上，
∴b=-4，D（-a，0），
∵直线y=mx与双曲线y=交于A、B两点，
∴A（-a，4），
∴AD⊥x轴，AD=4，
∵△ABD的面积为6，
∴S△ABD=AD×2a=6
∴a=，
∴点B坐标为（，-4）
本题考查反比例函数的性质，反比例函数图象是以原点为对称中心的双曲线，根据反比例函数的对称性表示出A点坐标是解题关键.
二、解答题（本大题共3个小题，共30分）
24、（1）当时，，当时，，；（2）点的坐标为，见解析；（3）当每月主叫时间小于130分钟时选择方式二省钱；当每月主叫时间等于130分钟时两种方式都一样；当每月主叫时间大于130分钟时选择方式一省钱.
【解析】
（1）根据题意即可写出两种资费的关系式；
（2）根据列表、描点、连线即可画出函数图像，再求出交点坐标A；
（3）根据函数图像的性质即可求解.
【详解】
解：（1）方式一：当时，，
当时，；
方式二：；
或解：（1）方式一：
化简，得；
方式二：；
（2）
点的坐标为
（3）由图象可得，
当每月主叫时间小于130分钟时选择方式二省钱；
当每月主叫时间等于130分钟时两种方式都一样；
当每月主叫时间大于130分钟时选择方式一省钱。
此题主要考查一次函数的应用，解题的关键是根据题意写出函数关系式.
25、（1）1；（2）2；（3）不存在．理由见解析
【解析】
【分析】（1）作AM⊥CD于M，由勾股定理求AM，再得CD=DM+CM=DM+AB；
（2）由题意：BP=AB﹣AP=10﹣2t．DQ=3t，根据：当BP=DQ时，四边形PBQD是平行四边形，可得10﹣2t=3t,可求t；
（3）作AM⊥CD于M，连接PQ．假设存在，则AP=MQ=3t﹣6，即2t=3t﹣6，求出的t不符合题意，故不存在.
【详解】解（1）如图1，作AM⊥CD于M，
则由题意四边形ABCM是矩形，
在Rt△ADM中，
∵DM2=AD2﹣AM2，AD=10，AM=BC=8，
∴AM=
=6，
∴CD=DM+CM=DM+AB=6+10=1．
（2）当四边形PBQD是平行四边形时，点P在AB上，点Q在DC上，
如图2中，由题意：BP=AB﹣AP=10﹣2t．DQ=3t，
当BP=DQ时，四边形PBQD是平行四边形，
∴10﹣2t=3t，
∴t=2，
（3）不存在．理由如下：
如图3，作AM⊥CD于M，连接PQ．
由题意AP=2t．DQ=3t，
由（1）可知DM=6，∴MQ=3t﹣6，
若2t=3t﹣6， 解得t=6，
∵AB=10，
∴t≤=5，
而t=6＞5，故t=6不符合题意，t不存在．
【点睛】本题考核知识点：动点，平行四边形，矩形. 解题关键点：此题是综合题，熟记性质和判定是关键.
26、；.
【解析】
根据分式的运算法则进行计算，即可求出答案．
【详解】
解：
原式
当时，
原式
本题考查分式的运算，解题的关键是熟练运用分式的运算法则，本题属于基础题型．
题号
一
二
三
四
五
总分
得分
批阅人
放水时间(分)
1
2
3
4
...
水池中水量(m)
38
36
34
32
...
分组/分
频数
频率
9≤x＜11
4
0.1
11≤x＜13
b
0.275
13≤x＜15
9
0.225
15≤x＜17
6
d
17≤x＜19
3
0.075
19≤x＜21
4
0.1
21≤x＜23
3
0.075
合计
a
c