初中人教版（2024）24.1.1 圆课后练习题

这是一份初中人教版（2024）24.1.1 圆课后练习题，共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题(每小题3分,共30分)
1平面内,已知☉O的半径是4 cm,线段OP=5 cm,则点P( )
A.在☉O外B.在☉O上C.在☉O内D.不能确定
2如图所示,MN为☉O的弦,∠N=50°,则∠MON的度数为( )
A.100°B.40°C.50°D.80°
3折扇最早出现于我国南北朝时期,《南齐书》中说:“司徒褚渊入朝,以腰扇障日.”这里的“腰扇”在《通鉴注》中的解释为折叠扇.如图,一折扇的骨柄长为21 cm,折扇张开后为扇形,圆心角∠AOB为120°,则AB的长为( )
A.7π cmB.14π cmC.21π cmD.42π cm
4如图,△ABC内接于☉O,∠C=46°,连接OA,则∠OAB=( )
A.44°B.45°C.54°D.67°
5如图,AB是☉O的弦,OC⊥AB交☉O于点C,点D是☉O上一点,∠ADC=30°,则∠BOC的度数为( )
A.30°B.40°C.50°D.60°
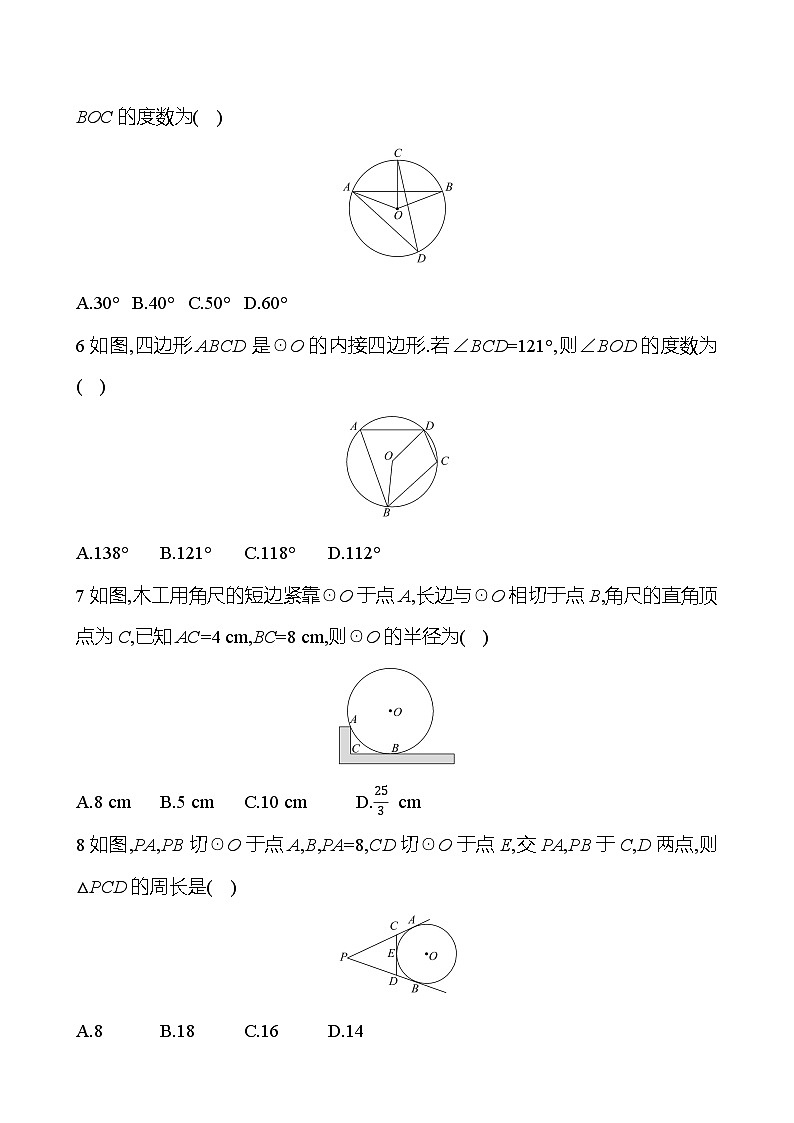
6如图,四边形ABCD是☉O的内接四边形.若∠BCD=121°,则∠BOD的度数为( )
A.138°B.121°C.118°D.112°
7如图,木工用角尺的短边紧靠☉O于点A,长边与☉O相切于点B,角尺的直角顶点为C,已知AC=4 cm,BC=8 cm,则☉O的半径为( )
A.8 cmB.5 cmC.10 cmD.253 cm
8如图,PA,PB切☉O于点A,B,PA=8,CD切☉O于点E,交PA,PB于C,D两点,则△PCD的周长是( )
A.8B.18C.16D.14
9如图,已知☉O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为( )
A.33B.32C.332D.3
10如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作☉O的切线CD,交AB于点D.则下列结论中错误的是( )
A.DC=DTB.AD=2DTC.BD=BOD.2OC=5AC
二、填空题(每小题3分,共24分)
11如图,AB是半圆O的直径,C,D是半圆上两点,BD=CD,过点C作☉O的切线与AB的延长线交于点E,若∠CEO=20°,则∠BOD的大小为 .
12如图所示的网格由边长为1个单位长度的小正方形组成,点A,B,C在直角坐标系中的坐标分别为(3,6),(-3,3),(7,-2),则△ABC内心的坐标为 .
13如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.若以AC所在直线为轴,把△ABC旋转一周,得到一个圆锥,则这个圆锥的侧面积等于 .
14如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如果C是☉O中弦AB的中点,CD经过圆心O交☉O于点D,并且AB=4 m,CD=6 m,则☉O的半径长为 m.
15如图,在正方形ABCD中,以点C为圆心,BC为半径作BD,在BD上取一点E,使AD=DE,则DE对应的圆心角的度数为 .
16如图,直线a⊥b,垂足为H,点P在直线b上,PH=4 cm,O为直线b上一动点,若以1 cm为半径的☉O与直线a相切,则OP的长为 .
17如图,正五边形ABCDE的边长为1,分别以点C,D为圆心,CD长为半径画弧,两弧交于点F,图中阴影部分的面积为 .(结果保留π)
18如图,Rt△ABC中,∠C=90°,AB=43,F是线段AC上一点,过点A的☉F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为 .
三、解答题(共46分)
19 (6分)某国产手机的手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.圆弧对应的弦AB长80 mm,弓形高CD长14 mm,求半径OA的长.

20(8分)已知:如图,AE是☉O的直径,AF⊥BC于D,求证:BF=CE.

21 (8分)小华用30°角的三角板和一块量角器进行数学实践探究活动,如图,她将三角板ADG的较短直角边AG和量角器(半圆O)的直径AB重合,斜边AD交半圆O于点C,较长直角边DG交半圆O于点E,根据量角器上的示数,可知点E为BC的中点.连接BC交DG于点F,连接BE.求证:EF=BF.

22(12分)如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与☉O的位置关系,并说明理由;
(2)若BD=23,AB=6,求阴影部分的面积(结果保留π).

23(12分)如图1,在△ABC中,AB=AC,☉O是△ABC的外接圆,过点C作∠BCD=
∠ACB,交☉O于点D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:ED=EC;
(2)求证:AF是☉O的切线;
(3)如图2,若点G是△ACD的内心,BC·BE=25,求BG的长.

【附加题】(10分)
如图,在边长为6的等边△ABC中,O是AB上的点,以O为圆心,OB的长为半径作圆交AB于点P,交BC于点N.
(1)如图1,点P与点A重合时,☉O交AC于点M.
①连接MN,△MNC的形状是__________;
②求MN的长.
(2)如图2,当OB=123-18时,求证:AC与☉O相切.
单元提优测评卷(四)(第二十四章)
(90分钟 100分)
一、选择题(每小题3分,共30分)
1平面内,已知☉O的半径是4 cm,线段OP=5 cm,则点P(A)
A.在☉O外B.在☉O上C.在☉O内D.不能确定
2如图所示,MN为☉O的弦,∠N=50°,则∠MON的度数为(D)
A.100°B.40°C.50°D.80°
3折扇最早出现于我国南北朝时期,《南齐书》中说:“司徒褚渊入朝,以腰扇障日.”这里的“腰扇”在《通鉴注》中的解释为折叠扇.如图,一折扇的骨柄长为21 cm,折扇张开后为扇形,圆心角∠AOB为120°,则AB的长为(B)
A.7π cmB.14π cmC.21π cmD.42π cm
4如图,△ABC内接于☉O,∠C=46°,连接OA,则∠OAB=(A)
A.44°B.45°C.54°D.67°
5如图,AB是☉O的弦,OC⊥AB交☉O于点C,点D是☉O上一点,∠ADC=30°,则∠BOC的度数为(D)
A.30°B.40°C.50°D.60°
6如图,四边形ABCD是☉O的内接四边形.若∠BCD=121°,则∠BOD的度数为(C)
A.138°B.121°C.118°D.112°
7如图,木工用角尺的短边紧靠☉O于点A,长边与☉O相切于点B,角尺的直角顶点为C,已知AC=4 cm,BC=8 cm,则☉O的半径为(D)
A.8 cmB.5 cmC.10 cmD.253 cm
8如图,PA,PB切☉O于点A,B,PA=8,CD切☉O于点E,交PA,PB于C,D两点,则△PCD的周长是(C)
A.8B.18C.16D.14
9如图,已知☉O的周长等于6π,则该圆内接正六边形ABCDEF的边心距OG为(C)
A.33B.32C.332D.3
10如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO.以O为圆心,OT为半径的圆交OA于点C,过点C作☉O的切线CD,交AB于点D.则下列结论中错误的是(D)
A.DC=DTB.AD=2DTC.BD=BOD.2OC=5AC
二、填空题(每小题3分,共24分)
11如图,AB是半圆O的直径,C,D是半圆上两点,BD=CD,过点C作☉O的切线与AB的延长线交于点E,若∠CEO=20°,则∠BOD的大小为 35° .
12如图所示的网格由边长为1个单位长度的小正方形组成,点A,B,C在直角坐标系中的坐标分别为(3,6),(-3,3),(7,-2),则△ABC内心的坐标为 (2,3) .
13如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.若以AC所在直线为轴,把△ABC旋转一周,得到一个圆锥,则这个圆锥的侧面积等于 15π .
14如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分,如果C是☉O中弦AB的中点,CD经过圆心O交☉O于点D,并且AB=4 m,CD=6 m,则☉O的半径长为 103 m.
15如图,在正方形ABCD中,以点C为圆心,BC为半径作BD,在BD上取一点E,使AD=DE,则DE对应的圆心角的度数为 60° .
16如图,直线a⊥b,垂足为H,点P在直线b上,PH=4 cm,O为直线b上一动点,若以1 cm为半径的☉O与直线a相切,则OP的长为 3 cm或5 cm .
17如图,正五边形ABCDE的边长为1,分别以点C,D为圆心,CD长为半径画弧,两弧交于点F,图中阴影部分的面积为 32-π15 .(结果保留π)
18如图,Rt△ABC中,∠C=90°,AB=43,F是线段AC上一点,过点A的☉F交AB于点D,E是线段BC上一点,且ED=EB,则EF的最小值为 2 3 .
三、解答题(共46分)
19 (6分)某国产手机的手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.圆弧对应的弦AB长80 mm,弓形高CD长14 mm,求半径OA的长.
解:设半径OA的长为r mm,则OA=OC=OB=r mm,
∵弓形高CD=14 mm,∴OD=(r-14)mm,∵OC⊥AB,AB=80 mm,∴AD=12AB=
40 mm,在Rt△OAD中,由勾股定理得:OA2-OD2=AD2,即r2-(r-14)2=402,解得r=4497.
答:半径OA的长为4497 mm.
20(8分)已知:如图,AE是☉O的直径,AF⊥BC于D,求证:BF=CE.
证明:∵AE是☉O的直径,∴∠ABE=90°,∴∠E+∠BAE=90°,
∵AF⊥BC于D,∴∠FAC+∠ACB=90°,
∵∠E=∠ACB,∴∠BAE=∠FAC,∴BE=CF,∴BF=CE,∴BF=CE.
21 (8分)小华用30°角的三角板和一块量角器进行数学实践探究活动,如图,她将三角板ADG的较短直角边AG和量角器(半圆O)的直径AB重合,斜边AD交半圆O于点C,较长直角边DG交半圆O于点E,根据量角器上的示数,可知点E为BC的中点.连接BC交DG于点F,连接BE.求证:EF=BF.
证明:如图,连接AE,
∵点E为BC的中点,
∴BE=CE,
∴∠BAE=∠CBE,
∵AB为直径,∴∠AEB=90°,
∴∠AEG+∠BEG=90°,
又∵∠AGD=90°,∴∠BAE+∠AEG=90°,
∴∠BEG=∠BAE,
∴∠BEG=∠CBE,∴EF=BF.
22(12分)如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与☉O的位置关系,并说明理由;
(2)若BD=23,AB=6,求阴影部分的面积(结果保留π).
解:(1)连接OD,如图,
∵OA=OD,∴∠OAD=∠ODA,
∵AD平分∠CAB,∴∠OAD=∠CAD,∴∠CAD=∠ODA,∴AC∥OD,
∴∠ODB=∠C=90°,即BC⊥OD,
又∵OD为☉O的半径,∴直线BC是☉O的切线;
(2)设OA=OD=r,则OB=6-r,
在Rt△ODB中,由勾股定理得:OD2+BD2=OB2,
∴r2+(23)2=(6-r)2,解得:r=2,
∴OB=4,OD=2,∴OD=12OB,∴∠B=30°,∴∠DOB=180°-∠B-∠ODB=60°,
∴阴影部分的面积S=S△ODB-S扇形DOF=12×23×2-60π×22360=23-2π3.
23(12分)如图1,在△ABC中,AB=AC,☉O是△ABC的外接圆,过点C作∠BCD=
∠ACB,交☉O于点D,连接AD交BC于点E,延长DC至点F,使CF=AC,连接AF.
(1)求证:ED=EC;
(2)求证:AF是☉O的切线;
(3)如图2,若点G是△ACD的内心,BC·BE=25,求BG的长.
解:(1)∵AB=AC,∴∠ABC=∠ACB,又∵∠ACB=∠BCD,∠ABC=∠ADC,
∴∠BCD=∠ADC,∴ED=EC;
(2)连接OA,∵AB=AC,∴AB=AC,∴OA⊥BC,∵CA=CF,∴∠CAF=∠CFA,
∴∠ACD=∠CAF+∠CFA=2∠CAF,
∵∠ACB=∠BCD,∴∠ACD=2∠ACB,∴∠CAF=∠ACB,∴AF∥BC,∴OA⊥AF,
∴AF为☉O的切线;
(3)∵∠ABE=∠CBA,∠BAD=∠BCD=∠ACB,∴△ABE∽△CBA,
∴ABBC=BEAB,∴AB2=BC·BE,∵BC·BE=25,∴AB=5,连接AG,
∴∠BAG=∠BAD+∠DAG,∠BGA=∠GAC+∠ACB,
∵点G为内心,∴∠DAG=∠GAC,又∵∠BAD=∠BCD=∠ACB,
∴∠BAD+∠DAG=∠GAC+∠ACB,∴∠BAG=∠BGA,∴BG=AB=5.
【附加题】(10分)
如图,在边长为6的等边△ABC中,O是AB上的点,以O为圆心,OB的长为半径作圆交AB于点P,交BC于点N.
(1)如图1,点P与点A重合时,☉O交AC于点M.
①连接MN,△MNC的形状是__________;
②求MN的长.
(2)如图2,当OB=123-18时,求证:AC与☉O相切.
解:(1)①连接OM,ON,
∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,
∵OA=OM,∴△AOM是等边三角形,∴∠AOM=60°,同理△BON是等边三角形,
∴∠BON=60°,∴∠MON=180°-60°-60°=60°,
又∵OM=ON,∴△MON是等边三角形,∴∠OMN=60°=∠OMA,
∴∠NMC=180°-60°-60°=60°,
又∵∠C=60°,∴△MCN是等边三角形.
答案:等边三角形
②由①知∠MON=60°,
∵点P与点A重合,∴☉O的半径为OM=OA=OB=12AB=3,
∴MN的长=nπr180=60π·3180=π.
(2)如图,过点O作OH⊥AC于点H,
∵△ABC是等边三角形,
∴∠A=60°,
在Rt△AOH中,OH⊥AC,∠A=60°,OA=AB-OB=24-123,
∴∠AOH=30°,AH=12OA=12-63,OH=OA2-AH2=123-18,
∵OH=OB=123-18,即OH为☉O的半径,
∴AC与☉O相切.