高中数学人教A版 (2019)必修 第一册4.4.2 对数函数的图象和性质图文ppt课件

这是一份高中数学人教A版 (2019)必修 第一册4.4.2 对数函数的图象和性质图文ppt课件，共60页。PPT课件主要包含了整体感知，探究建构，定义域，同增异减，应用迁移，1＋∞，－∞2等内容，欢迎下载使用。

[学习目标]　能解决与对数型函数的单调性、值域、奇偶性等相关的问题．(逻辑推理、数学运算)[讨论交流]　预习教材P134－P135，并思考以下问题：问题1．反函数与原函数的图象间存在怎样的联系？问题2．如何判断对数型函数的单调性、值域、奇偶性？[自我感知]　经过认真预习，结合你对本节课的理解和认识，请画出本节课的知识逻辑体系．
探究1　反函数探究问题　(1)函数f (x)＝2x与g(x)＝lg2x的定义域、值域之间有什么关系？(2)在同一坐标系中，函数f (x)＝2x与g(x)＝lg2x的图象有什么关系？
提示：(1)f (x)的定义域、值域分别是g(x)的值域、定义域．(2)f (x)与g(x)的图象关于直线y＝x对称．
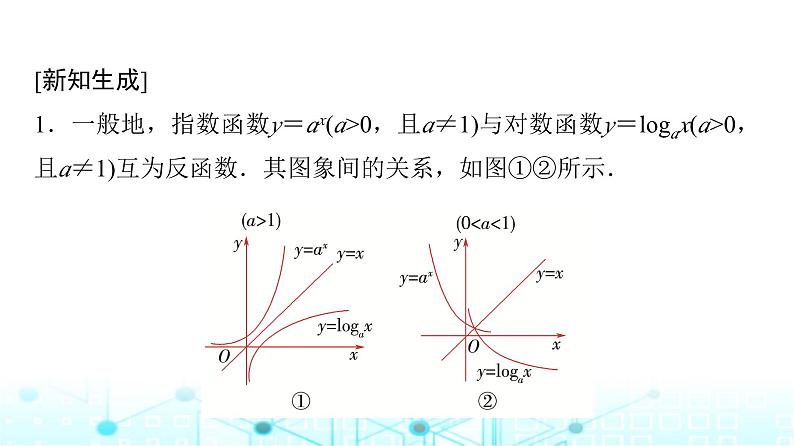
[新知生成]1．一般地，指数函数y＝ax(a>0，且a≠1)与对数函数y＝lgax(a>0，且a≠1)互为反函数．其图象间的关系，如图①②所示．
2．互为反函数的两个函数的性质(1)互为反函数的两个函数的图象关于直线y＝x对称．(2)原函数的图象过点(a，b)，反函数的图象必过点(b，a)．(3)原函数的定义域是反函数的值域，原函数的值域是反函数的定义域．(4)互为反函数的两个函数的单调性相同．
探究2　对数型复合函数的单调性[典例讲评]　1．讨论函数f (x)＝lga(3x2－2x－1)的单调性．
发现规律　形如f (x)＝lgag(x)(a>0，且a≠1)的函数的单调区间的求法：第一步：求函数f (x)的______；第二步：求函数________在定义域上的单调区间；第三步：应用复合函数单调性的“________”原则，得出f (x)＝lgag(x)(a>0，且a≠1)的单调区间．
反思领悟　对于形如y＝lga f (x)(a>0，且a≠1)的复合函数，其值域的求解步骤如下：(1)分解成y＝lgau，u＝f (x)两个函数．(2)求u的取值范围，注意u>0．(3)利用y＝lgau的单调性求值域．
[解]　(1)因为x2＋4≥4，所以lg2(x2＋4)≥lg24＝2．所以y＝lg2(x2＋4)的值域为[2，＋∞)．
探究4　对数型复合函数的奇偶性[典例讲评]　3．已知函数f (x)＝lg (2＋x)＋lg (2－x)．(1)求函数y＝f (x)的定义域；(2)判断函数y＝f (x)的奇偶性；(3)若f (m－2)＜f (m)，求m的取值范围．
反思领悟　对数函数本身不具有奇偶性，但有些函数与对数函数复合后，就具有奇偶性了，如y＝lga|x|就是偶函数．一般利用函数奇偶性的定义，并结合对数的运算性质来判断这类函数的奇偶性．
【链接·教材例题】例4　溶液酸碱度的测量．溶液酸碱度是通过pH计量的．pH的计算公式为pH＝－lg [H＋]，其中 [H＋]表示溶液中氢离子的浓度，单位是摩尔/升．(1)根据对数函数性质及上述pH的计算公式，说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系；(2)已知纯净水中氢离子的浓度为[H＋]＝10-7摩尔/升，计算纯净水的pH．
4．函数f (x)＝lg3(x2＋2x＋4)的值域为____________．
[1，＋∞)　[令u＝x2＋2x＋4，则u＝(x＋1)2＋3≥3，∴lg3(x2＋2x＋4)≥lg33＝1，即函数f (x)＝lg3(x2＋2x＋4)的值域为[1，＋∞)．]
1．知识链：(1)反函数；(2)对数型函数的单调性、值域、奇偶性．2．方法链：数形结合法．3．警示牌：讨论对数型函数的单调性时注意不要忽视其定义域．
回顾本节知识，自主完成以下问题：1．互为反函数的两个函数图象有什么特点？
[提示]　关于直线y＝x对称．
2．求解形如f (x)＝lgag(x)(a>0，且a≠1)的函数的单调性需注意哪些问题？
[提示]　首先注意函数的定义域，其次求解时注意满足“同增异减”的原则．
3．若f (x)∈(m，＋∞)，则y＝lgaf (x)(a>1)的值域一定是(lgam，＋∞)吗？
[提示]　不一定，必须保证m>0才可以．
课时分层作业(三十六)　对数函数的图象和性质(二)
2．函数f (x)＝lg |x|为(　　)A．奇函数，在区间(0，＋∞)上单调递减B．奇函数，在区间(0，＋∞)上单调递增C．偶函数，在区间(－∞，0)上单调递增D．偶函数，在区间(－∞，0)上单调递减
D　[已知函数的定义域为(－∞，0)∪(0，＋∞)，关于坐标原点对称，且f (－x)＝lg |－x|＝lg |x|＝f (x)，所以它是偶函数．当x>0时，f (x)＝lg x在区间(0，＋∞)上单调递增，又因为f (x)为偶函数，所以f (x)＝lg |x|在区间(－∞，0)上单调递减．]
4．若函数f (x)＝lg2(x2－ax－3a)在区间(－∞，－2]上单调递减，则实数a的取值范围是(　　)A．(－∞，4) B．(－4，4]C．(－∞，－4)∪[2，＋∞) D．[－4，4)
5．(多选)已知函数f (x)＝(lg2x)2－lg2x2－3，则下列说法正确的是(　　)A．f (4)＝－3B．函数y＝f (x)的图象与x轴有两个交点C．函数y＝f (x)的最小值为－4D．函数y＝f (x)的最大值为4
二、填空题6．函数f (x)＝lg5(2x＋1)的单调递增区间是____________．
7．函数y＝lg (100－x2)的值域是____________．
(－∞，2]　[令t＝100－x2，则0三、解答题9．已知f (x)＝lga(1－x)＋lga(x＋3)(a>0，且a≠1)．(1)求函数f (x)的定义域、值域；(2)若函数f (x)有最小值－2，求a的值．
11．设偶函数f (x)＝lga|x－b|在(－∞，0)上单调递增，则f (a＋1)与f (b＋2)的大小关系是(　　)A．f (a＋1)f (b＋2)
D　[因为函数f (x)是偶函数，所以b＝0，又函数在(－∞，0)上单调递增，所以函数在(0，＋∞)上单调递减，则0f (b＋2)．]
12．已知函数f (x)＝ln x＋ln (2－x)，则(　　)A．f (x)在(0，2)上单调递增B．f (x)在(0，2)上单调递减C．y＝f (x)的图象关于直线x＝1对称D．y＝f (x)的图象关于点(1，0)对称
C　[ f (x)的定义域为(0，2)．f (x)＝ln x＋ln (2－x)＝ln [x(2－x)]＝ln (－x2＋2x)．设u＝－x2＋2x，x∈(0，2)，则u＝－x2＋2x在(0，1)上单调递增，在(1，2)上单调递减．又y＝ln u在其定义域上为增函数，∴f (x)＝ln (－x2＋2x)在(0，1)上单调递增，在(1，2)上单调递减．∴选项A，B错误．
∵f (x)＝ln x＋ln (2－x)＝f (2－x)，∴f (x)的图象关于直线x＝1对称，∴选项C正确．∵f (2－x)＋f (x)＝[ln (2－x)＋ln x]＋[ln x＋ln (2－x)]＝2[ln x＋ln (2－x)]，不恒为0，∴f (x)的图象不关于点(1，0)对称，∴选项D错误．故选C．]
所以f (2x－x2)＝－lg2(2x－x2)，定义域满足2x－x2>0⇒x(2－x)>0⇒0[解]　∵f (x)是R上的偶函数，∴它的图象关于y轴对称．∵f (x)在[0，＋∞)上单调递增，∴f (x)在(－∞，0]上单调递减，