高中数学人教A版 (2019)必修 第一册5.5.1 两角和与差的正弦、余弦和正切图文ppt课件

这是一份高中数学人教A版 (2019)必修 第一册5.5.1 两角和与差的正弦、余弦和正切图文ppt课件，共60页。PPT课件主要包含了整体感知，探究建构，应用迁移等内容，欢迎下载使用。
[学习目标]　1．能利用两角和与差的正弦、余弦公式推导出两角和与差的正切公式．(逻辑推理)2．能利用两角和与差的正切公式进行化简、求值、证明．(数学运算)3．熟悉两角和与差的正切公式的常见变形，并能灵活应用．(数学运算)
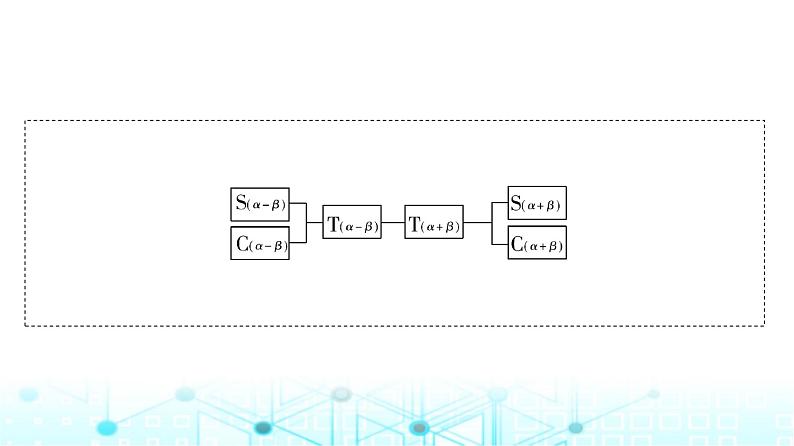
[讨论交流]　预习教材P218－P220，并思考以下问题：问题1．两角和与差的正切公式是什么？如何推导？问题2．两角和与差的正切公式的常用变形有哪些？[自我感知]　经过认真预习，结合你对本节课的理解和认识，请画出本节课的知识逻辑体系．
探究1　两角和与差的正切公式探究问题1　怎样由两角和的正弦、余弦公式得到两角和的正切公式？
探究问题2　由两角和的正切公式如何得到两角差的正切公式？
提示：用“－β”替换tan (α＋β)中的角β．
[典例讲评]　2．求值：(1)tan 67°－tan 22°－tan 67°·tan 22°；(2)(1＋tan 18°)(1＋tan 27°)．
[解]　(1)∵tan 67°－tan 22°＝tan (67°－22°)(1＋tan 67°tan 22°)＝tan 45°(1＋tan 67°tan 22°)＝1＋tan 67°tan 22°，∴tan 67°－tan 22°－tan 67°tan 22°＝1＋tan 67°tan 22°－tan 67°tan 22°＝1．(2)(1＋tan 18°)(1＋tan 27°)＝1＋tan 18°＋tan 27°＋tan 18°tan 27°＝1＋tan 45°(1－tan 18°tan 27°)＋tan 18°tan 27°＝2．
反思领悟　若化简的式子中出现了“tan α±tan β”及“tan α·tan β”两个整体，常考虑tan (α±β)的变形公式．
反思领悟　探究利用公式T(α±β)求角的步骤(1)求值：根据题设条件求角的某一三角函数值．(2)确定所求角的范围(范围讨论的过大或过小，会使求出的角不合题意或漏解)，根据范围找出角．
【教用·备选题】1．若α，β均为钝角，且(1－tan α)(1－tan β)＝2，求α＋β．
[解]　∵(1－tan α)(1－tan β)＝2，∴1－(tan α＋tan β)＋tan αtan β＝2，∴tan α＋tan β＝tan αtan β－1，
分析：和、差角公式把α±β的三角函数式转化成了α，β的三角函数式．如果反过来，从右到左使用公式，就可以将上述三角函数式化简．
2．设tan α，tan β是方程x2－3x＋2＝0的两个根，则tan (α＋β)的值为(　　)A．－3 B．－1C．1 D．3
3．在△ABC中，tan A＋tan B＝p，tan A tan B＝1－p，其中p≠0，则角C＝________．
4．计算tan 10°＋tan 35°＋tan 10°tan 35°＝________．
1．知识链：(1)两角和与差的正切公式的推导；(2)公式的正用、逆用、变形用．2．方法链：整体意识．3．警示牌：注意不要记错公式中的加减符号．
回顾本节知识，自主完成以下问题：你能分析一下T(α±β)公式的特征吗？
[提示]　公式的右边为分式形式，其中分子为tan α，tan β的和或差，分母为1与tan αtan β的差或和．公式中左边的加减号与右边分子上的加减号相同，与分母上的加减号相反．
符号变化规律可简记为“分子同，分母反”．
课时分层作业(五十四)　两角和与差的正切公式
二、填空题6．已知tan α＋tan β＝2，tan (α＋β)＝4，则tan αtan β＝________．
11．(1＋tan 1°)(1＋tan 2°)·…·(1＋tan 44°)(1＋tan 45°)的值为(　　)A．222 B．223C．224 D．225
B　[若α＋β＝45°，则(1＋tan α)(1＋tan β)＝1＋tan α＋tan β＋tan αtan β＝1＋tan (α＋β)(1－tan αtan β)＋tan αtan β＝1＋tan 45°(1－tan αtan β)＋tan αtan β＝1＋1－tan αtan β＋tan αtan β＝2．∴(1＋tan 1°)(1＋tan 2°)·…·(1＋tan 44°)(1＋tan 45°)＝223．故选B．]