浙教版八年级数学下册期中期末挑战满分冲刺卷特训11期末选填压轴题(浙江精选归纳)(原卷版+解析)

这是一份浙教版八年级数学下册期中期末挑战满分冲刺卷特训11期末选填压轴题(浙江精选归纳)(原卷版+解析)，共65页。试卷主要包含了单选题，填空题等内容，欢迎下载使用。
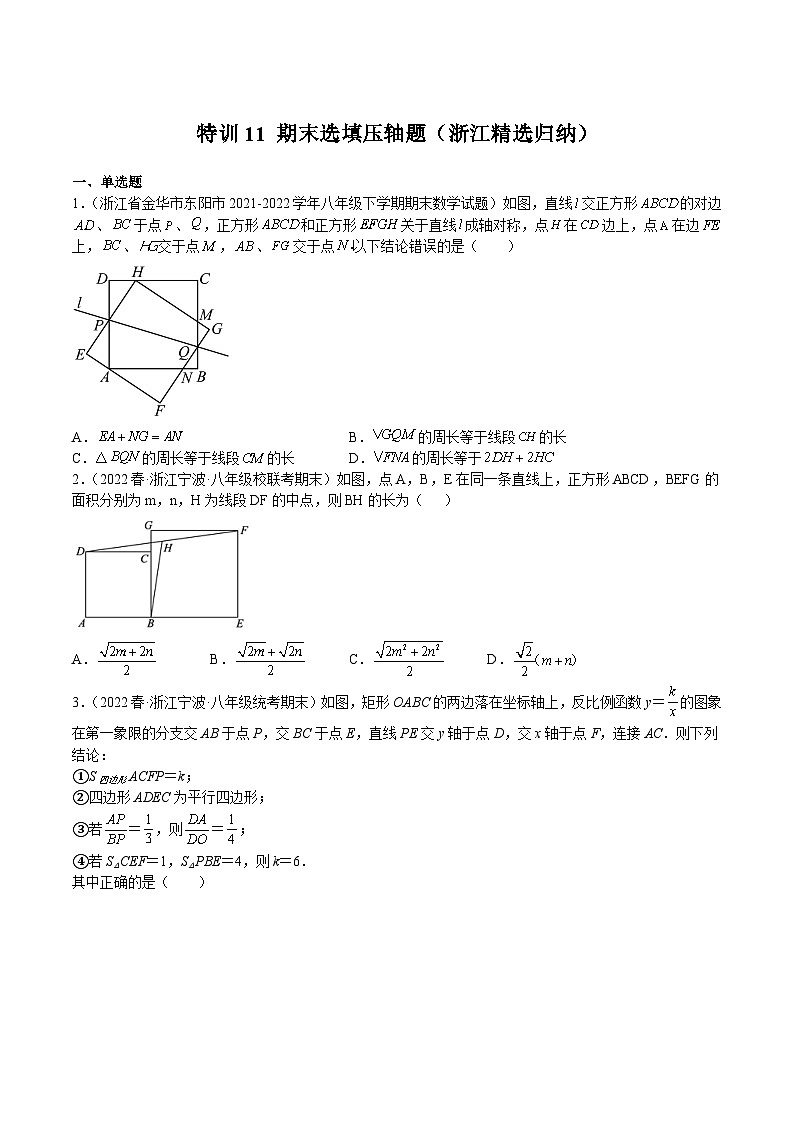
1．（浙江省金华市东阳市2021-2022学年八年级下学期期末数学试题）如图，直线交正方形的对边、于点、，正方形和正方形关于直线成轴对称，点在边上，点在边上，、交于点，、交于点以下结论错误的是（ ）
A．B．的周长等于线段的长
C．的周长等于线段的长D．的周长等于
2．（2022春·浙江宁波·八年级校联考期末）如图，点A，B，E在同一条直线上，正方形ABCD，BEFG的面积分别为m，n，H为线段DF的中点，则BH的长为（ ）
A．B．C．D．
3．（2022春·浙江宁波·八年级统考期末）如图，矩形OABC的两边落在坐标轴上，反比例函数y＝的图象在第一象限的分支交AB于点P，交BC于点E，直线PE交y轴于点D，交x轴于点F，连接AC．则下列结论：
①S四边形ACFP＝k；
②四边形ADEC为平行四边形；
③若＝，则＝；
④若S△CEF＝1，S△PBE＝4，则k＝6．
其中正确的是（ ）
A．①②④B．①②C．②④D．①③
4．（2022春·浙江金华·八年级统考期末）如图1，点P为矩形ABCD边上的一个动点，点P从A出发沿着矩形的四条边运动，最后回到A．设点P运动的路程长为x，△ABP的面积为y，图2是y随x变化的函数图像，则矩形ABCD的对角线BD的长是（ ）
A．B．C．8D．10
5．（2022春·浙江杭州·八年级统考期末）已知函数（为常数，且，），函数的图象和函数的图象关于直线对称．
①函数的图象上的点的纵坐标都小于2．
②若当（为大于0的实数）时，的最大值为，则在此取值范围内，的最小值必为．
则下列判断正确的是（ ）
A．①②都正确B．①正确，②错误C．①错误，②正确D．①②都错误
6．（2022春·浙江宁波·八年级统考期末）如图是一个由5张纸片拼成的菱形ABCD，相邻纸片之间互不重叠也无空隙，其中周围四张小平行四边形纸片都全等，中间一张纸片的面积为．连结BE，BG，DE，DG，四边形BEDG的面积为，若，则周围小平行四边形的宽与长的比值为（ ）
A．B．C．D．
7．（2022春·浙江绍兴·八年级统考期末）如图，在平面直角坐标系中，正方形，，，，…按如图所示的方式放置，其中点在轴上，点，，，，，，…在轴上，已知正方形的边长为2，，…．则点的纵坐标为（ ）
A．B．C．D．
8．（2022春·浙江杭州·八年级统考期末）已知是矩形对角线的交点，作，，相交于点，连接．下列说法正确的是( )
①四边形为菱形；②；③；④若，则
A．①③B．①②④C．①④D．③④
9．（2022春·浙江丽水·八年级统考期末）如图，在正方形中，，点，分别是射线，射线上的点，，与交于点．过点作，交直线于点，则的长是（ ）
A．8B．C．6D．
10．（2022春·浙江绍兴·八年级统考期末）如图在边长为1的小正方形构成的5×4的网格中，定义：以网格中的格点为顶点的正方形叫做格点正方形．则图中完全包含“ ”的格点正方形最多能画（ ）
A．13个B．16个C．19个D．21个
11．（2022春·浙江金华·八年级统考期末）如图，在平面直角坐标系中，矩形ABCO，点B(10，8)，点D在BC边上，连接AD，把ABD沿AD折叠，使点B恰好落在OC边上点E处，反比例函数（k≠0）的图象经过点D，则k的值为（ ）
A．20B．30C．40D．48
12．（2022春·浙江湖州·八年级统考期末）如图，在平行四边形ABCD中，AD＝3，AB＝，∠B是锐角，AE⊥BC于点E，F为AB中点，连接DF，EF，若∠EFD＝90°，则AE的长是（ ）
A．2B．3C．D．
13．（2022春·浙江湖州·八年级统考期末）如图，分别以的边，为一边向外作正方形和正方形，连结，，．若，，则的值为（ ）．
A．291B．219C．340D．170
14．（2022春·浙江宁波·八年级统考期末）如图，中∠ACB是直角，分别以的三边向外作正方形，G为边EF的中点，若要求出图中阴影的面积，只需要知道线段（ ）
A．AB的长度B．AC的长度C．BC的长度D．BG的长度
15．（2022春·浙江宁波·八年级统考期末）如图，正方形和正方形是两个全等的正方形，将它们按如图的方式放置在正方形内，若求阴影图形的面积，则只需知道( )
A．的面积B．五边形的面积
C．的面积D．正方形的面积
16．（2022春·浙江金华·八年级统考期末）如图，在平面直角坐标系xOy中，直线与x轴交于点A、与y轴交于点B，过点A作轴，交反比例函数的图象于点C，过点C作轴于点D，与直线交于点E，若，则k与a的关系正确的是( )
A．B．C．D．
17．（2022春·浙江温州·八年级统考期末）如图，线段与相交于点，，，以和为边作，以和为边作，且和的面积都为，若，则线段的取值范围是（ ）
A．B．
C．D．
18．（2022春·浙江·八年级统考期末）如图，直线AC与反比例函数的图像交于A，C两点（点A在点C的左边），与x轴交于点B，以点A为顶点向下作矩形ADMN，其对角线相交于点O，且AD平分∠OAB，AC =CB，连结CD，若△ACD的面积为6，则k的值为（ ）
A．8B．10C．12D．16
二、填空题
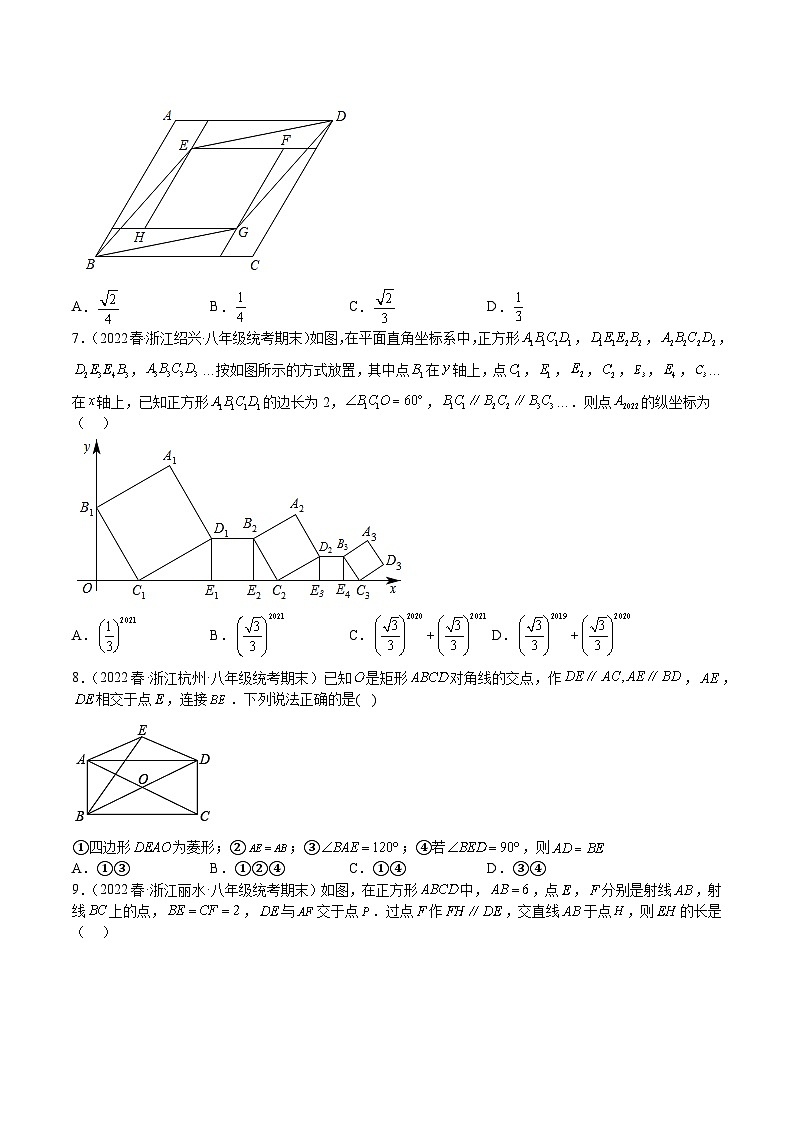
19．（2022春·浙江杭州·八年级杭州外国语学校校考期末）如图，在正方形中，，点O是对角线的中点，点Q是线段上的动点（点Q不与点O，A重合），连结，并延长交边于点E，过点Q作交于点F，分别连结与，交对角线于点G，过点C作交于点H，连结．以下四个结论：①；②周长为8；③，④线段的最小值为．其中正确的结论是 _____．（填序号）
20．（2022春·浙江金华·八年级统考期末）如图，在直角坐标系中，直线交坐标轴于、两点，函数的图象为曲线．（1）若曲线与直线有唯一的公共点，则______；（2）若曲线使得线段上的整点（横纵坐标均为整数的点，且不包括点、）分布在它的两侧，每侧的整点个数相同，则的取值范围为______．
21．（2022春·浙江舟山·八年级校联考期末）如图，矩形ABCD中，BC＝10，∠BAC＝30°，若在AC、AB上各取一点M、N，使BM+MN的值最小，求这个最小值_____．
22．（2022春·浙江宁波·八年级校联考期末）如图，是矩形内的任意一点，连接，，，，得到，，，设它们的面积分别是，，，，给出如下结论：
；
；
若，则；
若，则点必在矩形的对角线上．
其中正确结论的序号是_______________把所有正确结论的序号都填在横线上．
23．（2022春·浙江台州·八年级统考期末）如图，矩形中，，，点P是边上的动点（不与C、D重合），以为边作菱形，使，若矩形有第二个顶点在菱形的边上，则_______．
24．（2022春·浙江金华·八年级统考期末）三折伞是我们生活中常用的一种伞，它的骨架是一个“移动副”和多个“转动副”组成的连杆机构，如图1是三折伞一条骨架的结构图，当“移动副”（标号1）沿着伞柄移动时，折伞的每条骨架都可以绕“转动副”（标号2—9）转动；图2是三折伞一条骨架的示意图，其中四边形CDEF和四边形DGMN都是平行四边形，AC=BC=14cm，DE=2cm，DN=1cm．已知关闭折伞后，点A、E、H三点重合，点B与点M重合．
（1）BN=______；
（2）当∠BAC=60°时，点H到伞柄AB距离为______．
25．（2022春·浙江宁波·八年级统考期末）如图，平面直角坐标系中，矩形OABC的边OC，OA分别在x轴和y轴上，反比例函数的图象与AB，BC分别交于点E，点F，若矩形对角线的交点D在反比例函数图象上，且EDOB，则点E的坐标是_______．
26．（2022春·浙江绍兴·八年级统考期末）如图，直线与反比例函数的图象相交于A、C两点，与x轴交于点D，过点D作轴交反比例函的图象于点E，连结，点B为y轴上一点，满足，且恰好平行于x轴．若，则k的值为________．
27．（浙江省丽水市2021-2022学年八年级下学期期末数学试题）如图，以，为边长的矩形面积为，以为边长的正方形面积为，已知．
（1）当时，则的值是______；
（2）若为整数，，则矩形和正方形的周长之和的值是______．
28．（2022春·浙江舟山·八年级统考期末）已知函数y=x+1的图象与x轴、y轴分别交于点C、B，与双曲线y交于点A、D．若AB+CD=BC，则k的值为 _____．
29．（2022春·浙江台州·八年级统考期末）小明同学学习了菱形的知识后，结合之前学习的赵爽弦图，编了一个菱形版“赵爽弦图”．如图，菱形ABCD中，∠ABC=60°，四边形EFGH是矩形，若FA=FB=2，则矩形EFGH的面积为______．
30．（2022春·浙江绍兴·八年级统考期末）如图，正方形ABCD边长为2，点E，F是对角线AC上的动点，且EF长度为1，连结BE，BF，则△BEF周长的最小值为______．
31．（2022春·浙江湖州·八年级统考期末）如图，在矩形ABCD中，AB＝2，AD＝，M为对角线BD所在直线的一个动点，点N是平面上一点．若四边形MCND为平行四边形，MN＝，则BM的值为 _____．
32．（2022春·浙江金华·八年级统考期末）如图，矩形中，点，，分别在，，边上，，，平分，，则线段的长为______，线段的长为______．
33．（2022春·浙江湖州·八年级统考期末）如图，在平面直角坐标系中，已知，C为线段的中点，点P是线段上的一个动点，连接，当的值为____________时，将沿边所在直线翻折后得到的与重叠部分的面积为面积的．
34．（2022春·浙江宁波·八年级统考期末）如图，正方形ABCD边长为2，F为对角线AC上的一个动点，过C作AC的垂线并截取，连接EF，周长的最小值为______．
35．（2022春·浙江宁波·八年级统考期末）如图，点是内一点，轴，轴，，，，若反比例函数的图像经过、两点，则的值是______．
36．（2022春·浙江金华·八年级统考期末）如图，在矩形ABCD中，，射线AE与BC边交于点E，点F是射线AE上的一点，点G在边AB上，以FG为边向上作菱形FGMN，若，当点G从点B运动到点A时，点N的运动路径长是_______．
37．（2022春·浙江温州·八年级统考期末）如图1是第32届夏季奥运会的会徽，它是由三种不同规格的全等矩形组成，代表了不同的国家、文化和思维方式，表达了多样性的融合．图2和图3为该会徽中的某一部分，如图2，三种矩形分别由三种不同的菱形依次连结各边中点得到，其中，．如图3，点恰好在的延长线上，则______度．若，则点，之间的距离为______．
38．（2022春·浙江杭州·八年级统考期末）如图是一张矩形纸片ABCD，点E在AC边上，把△DCE沿直线DE折叠，使点C落在对角线BD上的点F处；点G在AB边上，把△DAG沿直线DG折叠，使点A落在线段DF上的点H处．若HF＝1，BF＝8，则BD＝______，矩形ABCD的面积＝______．
39．（2022春·浙江·八年级统考期末）如图，在矩形ABCD中，将矩形ABCD沿EF折叠，点A落在点处，点B落在CD边点处，连结B交EF于点G，点M在上，M=2M，若CD=3，AD=6，在折叠的过程中，点在边CD上不同的位置时，则MG+G的最小值为______．
特训11 期末选填压轴题（浙江精选归纳）
一、单选题
1．（浙江省金华市东阳市2021-2022学年八年级下学期期末数学试题）如图，直线交正方形的对边、于点、，正方形和正方形关于直线成轴对称，点在边上，点在边上，、交于点，、交于点以下结论错误的是（ ）
A．B．的周长等于线段的长
C．的周长等于线段的长D．的周长等于
【答案】C
【分析】过点作AK垂直于，垂足为，连接，根据两正方形关于直线对称，可得，，再根据边的转化即可证明A选项不符合题意；根据对称可得，将的周长表示出来，在通过边的转化即可证明B选项不符合题意；根据对称可得，即可证明C选项符合题意；根据对称，可得，将周长表示出来，再根据边的转化即可证明D选项不符合题意．
【解析】解：如图，过点作垂直于，垂足为，连接，
则，
∵正方形和正方形关于直线成轴对称，
∴，
在和中，
∴，
∴，
同理可证：，
∴，
∴，故A选项不符合题意；，
∵正方形和正方形关于直线成轴对称，
∴，
∴，
∵，
∴，故B选项不符合题意；
由正方形和正方形关于直线成轴对称，可得，，
∴，故C选项符合题意；
由正方形和正方形关于直线成轴对称，可得，，
∵，
∴，
∴
，
故D选项不符合题意．
故选：C．
【点睛】本题考查了正方形的性质，轴对称图形的性质，直角三角形全等的判定，熟练掌握轴对称图形的性质是解题关键．
2．（2022春·浙江宁波·八年级校联考期末）如图，点A，B，E在同一条直线上，正方形ABCD，BEFG的面积分别为m，n，H为线段DF的中点，则BH的长为（ ）
A．B．C．D．
【答案】A
【分析】连接BD，BF可证△ DBF为直角三角形，在通过直角三角形中斜边上的中线等于斜边的一半即可
【解析】如图连接BD，BF；
∵四边形ABCD和四边形BEFG都为正方形，AB=m，BE=n，
∴∠ DBF=90°，DB=，BF=，
∴DF=，
∵H为DF的中点，
∴ BH==，故选A
【点睛】熟练掌握直角三角形中斜边上的中线等于斜边的一半和辅助线作法是解决本题的关键
3．（2022春·浙江宁波·八年级统考期末）如图，矩形OABC的两边落在坐标轴上，反比例函数y＝的图象在第一象限的分支交AB于点P，交BC于点E，直线PE交y轴于点D，交x轴于点F，连接AC．则下列结论：
①S四边形ACFP＝k；
②四边形ADEC为平行四边形；
③若＝，则＝；
④若S△CEF＝1，S△PBE＝4，则k＝6．
其中正确的是（ ）
A．①②④B．①②C．②④D．①③
【答案】A
【分析】设点B的坐标为(b,a)，则得A(0,a)，C(b,0)，从而可求出P，E，再求出直线PE的解析式为，进而求得F(,0)，判断出四边形ACFP是平行四边形，计算得此四边形的面积，从而判断①正确；由四边形ACFP是平行四边形，得AC∥DF，故可得②正确；由，判断得ab=4k，再求出点D的坐标，即可判断③错误；由S△CEF＝1，得出＝2，再由S△PBE＝4，得到关于k的方程，解方程得k=6，从而可判断④正确．
【解析】设点B的坐标为(b,a)，
∵四边形ABCD为矩形，
∴A(0,a)，C(b,0)，
∵点P，E在反比例函数图形上，
∴P，E ，
∴直线PE的解析式为，
令y＝0，则，
∴x＝，
∴F(,0)，
∴CF＝+b﹣b＝，
∵P(，a)，
∴AP＝，
∴AP＝CF，
∵四边形OABC是矩形，
∴，
∴四边形ACFP是平行四边形，
∴S四边形ACFP＝CF•OA＝•a＝k，故①正确；
∵四边形ACFP是平行四边形，
∴AC∥DF，
∵OA∥BC，
∴四边形ADEC是平行四边形，故②正确；
∵，
∴，
∵B(b,a)，
∴OB＝b，
∵P(,a)，
∴AP＝，
∴，
∴ab＝4k，
∵直线PE的解析式为，
∴D，
∵A(0,a)，
∴AD＝+a﹣a＝，
∴＝＝＝，故③错误；
∵S△CEF＝1，
∴＝1，
∴＝2，
∵S△PBE＝4，
∴(b﹣)•(a﹣)＝4，
∴ab﹣k﹣k+＝8，
∴k2﹣2k﹣6＝0，
∴k＝﹣2（舍）或k＝6，故④正确，
∴正确的有①②④，
故选：A．
【点睛】本题是反比例函数的综合题，主要考查了矩形的性质，三角形和平行四边形的面积，平行四边形判定和性质，待定系数法，关键是判断四边形APFC是平行四边形．
4．（2022春·浙江金华·八年级统考期末）如图1，点P为矩形ABCD边上的一个动点，点P从A出发沿着矩形的四条边运动，最后回到A．设点P运动的路程长为x，△ABP的面积为y，图2是y随x变化的函数图像，则矩形ABCD的对角线BD的长是（ ）
A．B．C．8D．10
【答案】B
【分析】根据图象，可得出矩形的长，根据的最大面积，可得出矩形的宽，利用勾股定理即得出对角线长度．
【解析】解：点P在AB边运动时，不构成三角形，此时的面积为0，
由函数图象可知AB＝5，
当点P在CD边运动时，的面积达到最大10，
此时，
解得BC＝4，
则对角线．
故选：B．
【点睛】本题考查勾股定理与读图能力，读懂图、掌握勾股定理是解题的关键．
5．（2022春·浙江杭州·八年级统考期末）已知函数（为常数，且，），函数的图象和函数的图象关于直线对称．
①函数的图象上的点的纵坐标都小于2．
②若当（为大于0的实数）时，的最大值为，则在此取值范围内，的最小值必为．
则下列判断正确的是（ ）
A．①②都正确B．①正确，②错误C．①错误，②正确D．①②都错误
【答案】A
【分析】根据反比例函数的性质以及轴对称的性质判断即可．
【解析】解：∵函数（k为常数，且k＞0，x＞0），
∴函数图象在第一象限，如图，
∴函数y的最小值大于0，
∵函数的图象和函数的图象关于直线y=1对称，
∴的最大值小于2，
∴函数的图象上的点的纵坐标都小于2．故①正确；
当m≤x≤2（m为大于0的实数）时，的最大值为a，则其对应点为（m，a），
那么，点（m，a）关于直线y=1的对称点为（m，2-a），
∴在此取值范围内，的最小值必为2-a，故②正确，
故选：A．
【点睛】本题考查了反比例函数图象上点的坐标特征，反比例函数的性质，坐标与图形变化-对称，数形结合是解题的关键．
6．（2022春·浙江宁波·八年级统考期末）如图是一个由5张纸片拼成的菱形ABCD，相邻纸片之间互不重叠也无空隙，其中周围四张小平行四边形纸片都全等，中间一张纸片的面积为．连结BE，BG，DE，DG，四边形BEDG的面积为，若，则周围小平行四边形的宽与长的比值为（ ）
A．B．C．D．
【答案】B
【分析】作辅助线构建平行四边形的高线，设小平行四边形的宽是x，长是x，DQ=h，PQ=h1，根据图形可知：S2=S菱形ABCD-4S△BGN-2S▱，S1=GH•（h-h1），根据S2＝S1代入计算可得结论．
【解析】解：如图，过点D作DP⊥BC，交BC的延长线于P，交MG的延长线于Q，
设小平行四边形的宽是x，长是y，DQ=h，PQ=h1，
∵周围四张小平行四边形纸片都全等，
∵EH=GH=FG=EF=y-x，
∴四边形EFGH是菱形，
∵S2＝S1，
∴，即，
∴，
∴．
故选：B．
【点睛】本题考查了菱形的性质和判定，平行四边形的性质和面积，用参数表示线段的长和面积并计算是解本题的关键．
7．（2022春·浙江绍兴·八年级统考期末）如图，在平面直角坐标系中，正方形，，，，…按如图所示的方式放置，其中点在轴上，点，，，，，，…在轴上，已知正方形的边长为2，，…．则点的纵坐标为（ ）
A．B．C．D．
【答案】C
【分析】利用正方形的性质、含30°角直角三角形性质及勾股定理得出A1的纵坐标，进而得出变化规律即可得出答案．
【解析】解：如图，过点A1作A1G1⊥x轴于点G1，过点B1作B1F1⊥A1G1于点F1，过点A2作A2G2⊥x轴于点G2，过点B2作B2F2⊥A2G2于点F2，
过点A3作A3G3⊥x轴于点G3，过点B3作B3F3⊥A3G3于点F3，
∵正方形A1B1C1D1的边长为2，∠B1C1O=60°，B1C1B2C2B3C3，
∴D1E1=B2E2，D2E3=B3E4，∠C1B1O=∠D1C1E1=∠C2B2E2=∠C3B3E4=30°，∠B1OC1=∠A1F1B1=90°，
∴D1E1=OC1=A1F1=B1C1=1，
∴E2B2=1，
在Rt△B1OC1中，OB1==，
∵∠OG1F1=∠B1OC1=∠G1F1B1=90°，
∴四边形OB1F1G1是矩形，
∴F1G1=OB1=，
∴A1G1=F1G1+A1F1=+1=（）-1+（）0，
即点A1的纵坐标为：（）-1+（）0；
同理可得：点A2的纵坐标为：（）0+（）1；
点A3的纵坐标为：（）1+（）2；
……
点A的纵坐标为：（）n-2+（）n-1；
∴点A2022的纵坐标为：（）2020+（）2021；
故选：C．
【点睛】本题考查了正方形的性质、含30°角直角三角形性质，勾股定理等知识，得出点A的纵坐标变化规律是解题关键．
8．（2022春·浙江杭州·八年级统考期末）已知是矩形对角线的交点，作，，相交于点，连接．下列说法正确的是( )
①四边形为菱形；②；③；④若，则
A．①③B．①②④C．①④D．③④
【答案】C
【分析】先证明四边形DEAO是平行四边形，再根据四边形ABCD是矩形，可得OA＝OD，进而得出四边形DEAO为菱形，①正确；当△AOB是等边三角形时，AE＝AB才能成立，②错误；当△AOB是等边三角形时，∠BAE＝120°才能成立，③错误；连接OE，求出OE＝OB＝OD，证明△DEO是等边三角形，可得∠ADB＝∠EBD＝30°，然后证明△ABD≌△EDB即可得出④正确．
【解析】解：①∵DEAC，AEBD，
∴四边形DEAO是平行四边形，
∵四边形ABCD是矩形，
∴OA＝OD，
∴四边形DEAO为菱形，故①正确；
②当△AOB是等边三角形时，AE＝AB才能成立，故②错误；
③当△AOB是等边三角形时，∠BAE＝120°才能成立，故③错误；
④如图，连接OE，

∵∠BED＝90°，O是矩形ABCD对角线BD的中点，
∴OE＝OB＝OD，
∵四边形DEAO为菱形，
∴DE＝OD，
∴△DEO是等边三角形，
∴∠EDO＝60°，
∴∠ADO＝∠EDO＝30°，∠EBD＝90°－60°＝30°，
∴∠ADB＝∠EBD，
又∵∠BAD＝∠DEB＝90°，BD＝DB，
∴△ABD≌△EDB（AAS），
∴AD＝BE，故④正确；
故选：C．
【点睛】本题考查了矩形的性质，菱形的判定与性质，全等三角形的判定与性质，等边三角形的判定和性质，直角三角形斜边中线的性质等知识，灵活运用各性质是解题的关键．
9．（2022春·浙江丽水·八年级统考期末）如图，在正方形中，，点，分别是射线，射线上的点，，与交于点．过点作，交直线于点，则的长是（ ）
A．8B．C．6D．
【答案】B
【分析】首先根据正方形的性质，得出，，然后再根据线段的关系，得出，再根据，得出，再根据全等三角形的性质，得出，然后再根据两直线平行，同位角相等，得出，再根据等量代换，得出，结合，得出，再根据相似三角形的性质，得出，进而算出的长，再根据线段之间的关系，即可得出的长．
【解析】解：∵四边形ABCD是正方形，
∴，，
又∵，
∴，
在和中，
，
∴，
∴，
又∵，
∴，
∴，
又∵，
∴，
∴，
∴，
解得：，
∴．
故选：B
【点睛】本题考查了正方形的性质、全等三角形的性质与判定、平行线的性质、相似三角形的性质与判定，解本题的关键在熟练掌握相关的性质与定理．
10．（2022春·浙江绍兴·八年级统考期末）如图在边长为1的小正方形构成的5×4的网格中，定义：以网格中的格点为顶点的正方形叫做格点正方形．则图中完全包含“ ”的格点正方形最多能画（ ）
A．13个B．16个C．19个D．21个
【答案】C
【分析】分七种情况讨论，可求解．
【解析】解：图中包含“”的格点正方形为：
边长为1的正方形有：1个，
边长为2的正方形有：4个，
边长为3的正方形有：6个，
边长为的正方形有：2个，
边长为4的正方形有：2个，
边长为的正方形有：2个，
边长为的正方形有：2个，
所以图中包含“ ”的格点正方形的个数为：1+4+6+2+2+2+2=19，
故选：C．
【点睛】此题考查了正方形的判定，图形的变化，结合图形正确进行分类讨论是解题的关键．
11．（2022春·浙江金华·八年级统考期末）如图，在平面直角坐标系中，矩形ABCO，点B(10，8)，点D在BC边上，连接AD，把ABD沿AD折叠，使点B恰好落在OC边上点E处，反比例函数（k≠0）的图象经过点D，则k的值为（ ）
A．20B．30C．40D．48
【答案】B
【分析】根据翻折变换的性质，可得AE＝AB＝5，DE＝BD；然后设点D的坐标是（10，b），在Rt△CDE中，根据勾股定理，求出CD的长度，进而求出k的值．
【解析】解：∵△ABD沿AD折叠，使点B恰好落在OC边上点E处，点B（10，8），
∴AE＝AB＝10，DE＝BD，
∵AO＝8，AE＝10，
∴OE＝＝6，CE＝10﹣6＝4，
设点D的坐标是（10，b），
则CD＝b，DE＝8﹣b，
∵CD2+CE2＝DE2，
∴b2+42＝（8﹣b）2，
解得b＝3，
∴点D的坐标是（10，3），
∵反比例函数的图象经过点D，
∴k＝10×3＝30，
故选：B．
【点睛】本题考查了求反比例函数的解析式，同时也考查了矩形的翻折问题．须熟练掌握待定系数法求反比例函数的解析式，轴对称的性质．其中求点D的坐标是解题的关键．
12．（2022春·浙江湖州·八年级统考期末）如图，在平行四边形ABCD中，AD＝3，AB＝，∠B是锐角，AE⊥BC于点E，F为AB中点，连接DF，EF，若∠EFD＝90°，则AE的长是（ ）
A．2B．3C．D．
【答案】C
【分析】延长EF交DA的延长线于Q，连接DE，设BE＝x．首先证明DQ＝DE＝x+3，利用勾股定理构建方程即可解决问题．
【解析】解：如图，延长EF交DA的延长线于Q，连接DE，设BE＝x，
∵四边形ABCD是平行四边形，
∴DQBC，
∴∠AQF＝∠BEF，
∵AF＝FB，∠AFQ＝∠BFE，
∴△QFA≌△EFB（AAS），
∴AQ＝BE＝x，QF＝EF，
∵∠EFD＝90°，
∴DF⊥QE，
∴DQ＝DE＝x+3，
∵AE⊥BC，BCAD，
∴AE⊥AD，
∴∠AEB＝∠EAD＝90°，
∵，
∴，
整理得：，
解得或（舍去），
∴BE＝1，
∴，
故选：C．
【点睛】此题考查了平行四边形的性质，全等三角形的性质和判定，勾股定理的应用，解题的关键是作辅助线构建直角三角形．
13．（2022春·浙江湖州·八年级统考期末）如图，分别以的边，为一边向外作正方形和正方形，连结，，．若，，则的值为（ ）．
A．291B．219C．340D．170
【答案】C
【分析】连接BE，CG，设BG与CE交于点O，CE与AG交于点P，可证明△ABG≌△AEC，可得∠AGB=∠ACE，再由三角形内角和定理可得∠POG=∠PAC=90°，再由勾股定理，即可求解．
【解析】解：如图，连接BE，CG，设BG与CE交于点O，CE与AG交于点P，
∵四边形和四边形为正方形，
∴AB=AE，AC=AG，∠BAE=∠CAG=90°，，
∴∠BAE+∠GAE=∠CAG+∠GAE，即∠BAG=∠EAC，
在△ABG和△AEC中，
，
∴△ABG≌△AEC（SAS），
∴∠AGB=∠ACE，
∵∠PGO+∠POG+∠GPO=∠PCA+∠PAC+∠APC，∠GPO=∠APC，
∴∠POG=∠PAC=90°，
∵，，，，
∴．
故选：C
【点睛】本题主要考查了正方形的性质，全等三角形的判定和性质，勾股定理等知识，熟练掌握正方形的性质，全等三角形的判定和性质，勾股定理是解题的关键．
14．（2022春·浙江宁波·八年级统考期末）如图，中∠ACB是直角，分别以的三边向外作正方形，G为边EF的中点，若要求出图中阴影的面积，只需要知道线段（ ）
A．AB的长度B．AC的长度C．BC的长度D．BG的长度
【答案】C
【分析】解法①代数法：如图，连接GC并延长，交AB于点H，根据题意得到FC=AC，EC=BC，且夹角为直角，利用SAS得到三角形全等，利用全等三角形对应角相等得到∠GFC=∠CAH，根据G为EF中点且直角三角形斜边上的中线等于斜边的一半，再利用等角的余角相等得到CH垂直AB，利用面积法表示出CH，根据勾股定理表示出BH，进而表示出阴影部分面积，即可作出判断．解法②几何法：根据平行线的性质，得，再证明，再由，得，即可得出答案．
【解析】解：解法①代数法
如图连接GC并延长交AB于点H，
设，，．易证，
∴，
∵G为EF的中点所以即，
∴，
∵，
∴，
∴，
即，
在中，，
∴，
在中由勾股定理可得，
∴．
故选：C.
解法②几何法：
如图连接AM，CD
由①得所以
易证
∵，
∴．
故选：C.
【点睛】本题考查正方形的性质，勾股定理，全等三角形的判定与性质，熟练掌握各自的性质及定理是解本题的关键
15．（2022春·浙江宁波·八年级统考期末）如图，正方形和正方形是两个全等的正方形，将它们按如图的方式放置在正方形内，若求阴影图形的面积，则只需知道( )
A．的面积B．五边形的面积
C．的面积D．正方形的面积
【答案】A
【分析】根据题意可知阴影部分的面积的面积的面积的面积，根据正方形的性质易证≌，可得的面积的面积，同理可得≌，的面积的面积，可知阴影部分的面积，即可进行选择．
【解析】解：正方形和正方形是两个全等的正方形，
正方形的面积正方形的面积，
正方形的面积五边形的面积正方形的面积五边形的面积，
阴影部分的面积的面积的面积的面积，
在正方形中，，
，
在正方形中，，，
，
，
≌，
的面积的面积，
同理可得≌，
的面积的面积，
阴影部分的面积，
只要知道的面积即可求出阴影部分的面积，
故选：A．
【点睛】本题考查了正方形的性质，全等三角形的判定和性质，熟练掌握这些性质是解题的关键．
16．（2022春·浙江金华·八年级统考期末）如图，在平面直角坐标系xOy中，直线与x轴交于点A、与y轴交于点B，过点A作轴，交反比例函数的图象于点C，过点C作轴于点D，与直线交于点E，若，则k与a的关系正确的是( )
A．B．C．D．
【答案】A
【分析】先求出A坐标，可以得到C的坐标，由CE=DE，可以得E的坐标，把E的坐标代入直线即可得出答案．
【解析】解：对于，
当x=0时，y=k；当y=0时，，
∴点A的坐标为，
∵轴，且点C在反比例函数的图象上，
∴点C的坐标为，
∵，轴，
∴点E的坐标为，
把E代入得：
，解得：．
故选：A
【点睛】本题考查了一次函数和反比例函数的交点问题，利用图象中各个点的坐标之间的关系是解此题的关键．
17．（2022春·浙江温州·八年级统考期末）如图，线段与相交于点，，，以和为边作，以和为边作，且和的面积都为，若，则线段的取值范围是（ ）
A．B．
C．D．
【答案】B
【分析】过A点作AN⊥CD于点N，过D点作DM⊥AB于M，根据平行四边形的面积公式，结合等腰直角三角形的性质可得CE•AE=DF•DE=6，利用DE+AE=9可得CE根据，即可求解．
【解析】解：过A点作AN⊥CD于点N，过D点作DM⊥AB于M，
∵，
∴
∴CE•AE=DF•DE=6，
∵DE+AE=9，
∴CE
∵，
，
即
解得．
故选B．
【点睛】本题主要考查平行四边形的性质，等腰直角三角形，解不等式组，勾股定理，求得CE是解题的关键．
18．（2022春·浙江·八年级统考期末）如图，直线AC与反比例函数的图像交于A，C两点（点A在点C的左边），与x轴交于点B，以点A为顶点向下作矩形ADMN，其对角线相交于点O，且AD平分∠OAB，AC =CB，连结CD，若△ACD的面积为6，则k的值为（ ）
A．8B．10C．12D．16
【答案】A
【分析】连接OC，分别过点A、C作x轴的垂线交x轴于点E、F，设点A（a，），首先证明AB∥OD，结合AC =CB可求出S△AOB＝2S△AOC＝12，然后证明△BCF∽△BAE，求出CF和OF，得到点C的坐标，然后将点C的坐标代入反比例函数解析式求出k即可．
【解析】解：如图，连接OC，
∵四边形ADMN是矩形，AD平分∠OAB，
∴OA＝OD，∠OAD＝∠BAD，
∴∠OAD＝∠ODA，
∴∠BAD＝∠ODA，
∴AB∥OD，
∴S△AOC＝S△ADC＝6，
∵AC =CB，
∴S△AOB＝2S△AOC＝12，
分别过点A、C作x轴的垂线交x轴于点E、F，设点A（a，），
则S△AOB＝，即，
∴，
∴，
∵AE⊥x轴，CF⊥x轴，
∴AE∥CF，
∴△BCF∽△BAE，
∴，
∴CF＝，EF＝，
∴OF＝，
∴点C的坐标为（，），
∵点C在反比例函数的图像上，
∴，
解得：，
故选：A．
【点睛】本题考查了矩形的性质，角平分线的定义，平行线的判定和性质，相似三角形的判定和性质以及反比例函数图像上点的坐标特征，作出合适的辅助线，证明△BCF∽△BAE是解答此题的关键．
二、填空题
19．（2022春·浙江杭州·八年级杭州外国语学校校考期末）如图，在正方形中，，点O是对角线的中点，点Q是线段上的动点（点Q不与点O，A重合），连结，并延长交边于点E，过点Q作交于点F，分别连结与，交对角线于点G，过点C作交于点H，连结．以下四个结论：①；②周长为8；③，④线段的最小值为．其中正确的结论是 _____．（填序号）
【答案】①②④
【分析】通过证明点B，点C，点F，点Q四点共圆，可得，，可证，故①正确；由“”可证，，可得，由线段的和差关系可得的周长为8，故②正确；由题意可得点H在以为边的圆上运动，则当点H在上时，有最小值为，故④正确；通过证明点E，点F，点G，点Q四点共圆，可判断③．
【解析】解：∵，
∴，
∴点B，点C，点F，点Q四点共圆，
∴，，
∴，
∴，故①正确；
如图，延长至N使，连接，
∵，
∴，
∴，
∵，
∴，
∵，
∴，
又∵，
∴，
∴，
∴的周长，故②正确；
∵，
∴，
∴点H在以为边的圆上运动，
如图，以为直径作圆，取BC的中点P，连接，
∴，
∴，
在中，，
∴当点H在上时，AH有最小值为，故④正确；
如图，连接，
∵，
∴点A，点B，点F，点E四点共圆，
∴，
∴，，
∴，
∴，
∵，
∴点E，点F，点G，点Q四点共圆，
∴，故③不正确．
故答案为：①②④．
【点睛】本题是四边形综合题，考查了正方形的性质，全等三角形的判定和性质，四点共圆等知识，添加恰当辅助线构造全等三角形是解题的关键．
20．（2022春·浙江金华·八年级统考期末）如图，在直角坐标系中，直线交坐标轴于、两点，函数的图象为曲线．（1）若曲线与直线有唯一的公共点，则______；（2）若曲线使得线段上的整点（横纵坐标均为整数的点，且不包括点、）分布在它的两侧，每侧的整点个数相同，则的取值范围为______．
【答案】
【分析】（1）由曲线与直线有唯一的公共点，可得只有一组解，从而得有两个相等的实数根，利用一元二次方程根的判别式即可求解；（2）先求得线段上的整点，由曲线使得线段上的整点横纵坐标均为整数的点，且不包括点、分布在它的两侧，每侧的整点个数相同，则曲线经过和之间即可求解．
【解析】解：（1）由题意得：只有一组解，
有两个相等的实数根，
，
解得：，
故答案为：；
（2）由，得，，
线段上的整数点共有个，分别为，，，，，，，．
当曲线经过点时，在曲线上方个，在曲线下方个；
当曲线经过点时，在曲线上方个，在曲线下方个；
若曲线使得线段上的整点横纵坐标均为整数的点，且不包括点、分布在它的两侧，每侧的整点个数相同，则曲线经过和之间，
当曲线经过点时，；
当曲线经过点时，．
的取值范围为：．
故答案为：．
【点睛】本题主要考查了一次函数与反比例函数的图像及性质，熟练掌握数形结合的思想是解题的关键．
21．（2022春·浙江舟山·八年级校联考期末）如图，矩形ABCD中，BC＝10，∠BAC＝30°，若在AC、AB上各取一点M、N，使BM+MN的值最小，求这个最小值_____．
【答案】15
【分析】作点N关于AC的对称点，作射线，根据对称性和垂线段最短可知： BM+MN的最小值为B到的垂线段即的长度．
【解析】作点N关于AC的对称点，作射线，
则有，，
∴．
作于，交AC于，
根据垂线段最短可知： BM+MN的最小值为的长度．
在矩形ABCD中，BC＝10，∠BAC＝30°，
∴AC=2BC=20，
∴．
∵，
∴．
又∵为B到的垂线段，
∴，
∴，
∴．
∴，
即BM+MN的最小值为15．
【点睛】本题考查含30°角的直角三角形的性质，勾股定理，与垂线段最短有关的最短路径问题，轴对称的性质等知识，根据题意得出BM+MN的最小值为B到的垂线段即的长度时解题的关键．
22．（2022春·浙江宁波·八年级校联考期末）如图，是矩形内的任意一点，连接，，，，得到，，，设它们的面积分别是，，，，给出如下结论：
；
；
若，则；
若，则点必在矩形的对角线上．
其中正确结论的序号是_______________把所有正确结论的序号都填在横线上．
【答案】②④/④②
【分析】根据三角形面积求法以及矩形性质得出矩形ABCD面积，及先判断出，得出,进而判断出点P在线段BD上，即可得出结论
【解析】解：如下图，过点P分别作于点F，于点E，
以AD为底边，以BC为底边,
∴此时两三角形高的和为AB，即可得出矩形ABCD面积；
同理得得出矩形ABCD面积
∴（故正确）
当点P为矩形的两条对角线的交点时，，
但点P是矩形ABCD内任意一点，所以该等式不一定成立（故①错误）
③若，只能得出与高度之比，不一定等于2，（故③错误）
④由（1）知，四边形AEPF是矩形
∴点P在矩形的对角线上，（故④正确）
故答案为：② ④
【点睛】本题主要考查了矩形的性质及三角形面积求法，根据已知得出是解题关键．
23．（2022春·浙江台州·八年级统考期末）如图，矩形中，，，点P是边上的动点（不与C、D重合），以为边作菱形，使，若矩形有第二个顶点在菱形的边上，则_______．
【答案】
【分析】根据题意，分两种情况讨论，①当点在上时，根据矩形的性质与菱形的性质，以及含30度角的直角三角形的性质，勾股定理可得；
②当点在菱形的边上时，如图，过点作交的延长线于点，线段上截取，过点作于,证明，根据等面积法即可求解．
【解析】解：①当点在上时，如图，
四边形是矩形，
，
，，
，
，
，
；
②如图，当点在菱形的边上时，如图，过点作交的延长线于点，
设，四边形是菱形，
，
在中，，
，
，，
，
线段上截取，过点作于,
，,
即，
解得（负值舍去），经检验符合题意，
，
综上所述，的长为或．
【点睛】本题考查了菱形的性质，矩形的性质，全等三角形的性质与判定，掌握以上知识是解题的关键．
24．（2022春·浙江金华·八年级统考期末）三折伞是我们生活中常用的一种伞，它的骨架是一个“移动副”和多个“转动副”组成的连杆机构，如图1是三折伞一条骨架的结构图，当“移动副”（标号1）沿着伞柄移动时，折伞的每条骨架都可以绕“转动副”（标号2—9）转动；图2是三折伞一条骨架的示意图，其中四边形CDEF和四边形DGMN都是平行四边形，AC=BC=14cm，DE=2cm，DN=1cm．已知关闭折伞后，点A、E、H三点重合，点B与点M重合．
（1）BN=______；
（2）当∠BAC=60°时，点H到伞柄AB距离为______．
【答案】 25
【分析】由关闭折伞后，点A、E、H三点重合，得到AC=CD+DE，求出CD得到CN，即可得到BN；根据平行线的性质求出∠AFE=∠EGH=120°，得到∠ EAF=∠AEF=∠GEH = 30°，求出AF=12，MN=BN=25，EG=HG=27，过F作FR⊥AE于R，过G作GT⊥AH于T，勾股定理求出AR得到AE的长，同理求出EH，即可得到答案．
【解析】∵关闭折伞后，点A、E、H三点重合，
∴AC=CD+DE，
∴CD=14-2=12，
∴CN=CD-DN=11，
∴BN=14+11=25(cm)，
如图2，A、E、H三点共线并且AH⊥AB，
∵∠BAC=60°，AC=BC=14，
∴∠ACB=60°，
∵ACDE， DGMN，
∴∠AFE=∠EGH=120°，
∵AF= EF，
∴∠ EAF=∠AEF=∠GEH = 30°，
∴AE⊥ AB，
∵关闭折伞后，点A、E、H三点重合，点B与点M重合，
∴AF=12，MN=BN=25，EG=HG=27，
过F作FR⊥AE于R，过G作GT⊥AH于T，
∴FR=AF=6，
∴AR=，
∴AE=2AR=，
同理可得EH=，
∴AН = AE+ EН =，
∴点H到伞柄AB距离为cm，
故答案为：25，．
【点睛】此题考查了线段的和差计算，勾股定理，平行四边形的性质，正确理解题意掌握各知识点是解题的关键．
25．（2022春·浙江宁波·八年级统考期末）如图，平面直角坐标系中，矩形OABC的边OC，OA分别在x轴和y轴上，反比例函数的图象与AB，BC分别交于点E，点F，若矩形对角线的交点D在反比例函数图象上，且EDOB，则点E的坐标是_______．
【答案】(2，4)
【分析】连接OE，根据反比例函数系数k的几何意义得到，设D(m，n)，则mn=，n=，进一步求得的面积，即可得到AE=，，由OD=BD，EDOB，得到OE=BE=，然后利用勾股定理得到整理得，由于，求得m=4，即可求出E点坐标．
【解析】解：连接OE，
∵反比例函数的图象与AB、BC分别交于点E、F，
∴，
，
设D(m，n)
∵矩形对角线的交点D在反比例函数的图象上，
∴mn=，n=，
∵矩形OABC的边OC，OA分别在x轴和y轴上，
∴B(2m，2n)
∴A=2n，AB=2m，
∴，
∴AE=，
∴BE，E(，)，
∴OA=，
∵OD=BD，EDOB，
∴OE=BE=，
在RtAOE中，，
∴
整理得
∵m0，
∴m=4，
∴E(2，4)，
故答案为：(2，4)．
【点睛】本题考查了矩形的性质、反比例函数k的几何意义勾股定理的应用和线段垂直平分线的性质，解决本题的关键是根据题意得到关于m的方程．
26．（2022春·浙江绍兴·八年级统考期末）如图，直线与反比例函数的图象相交于A、C两点，与x轴交于点D，过点D作轴交反比例函的图象于点E，连结，点B为y轴上一点，满足，且恰好平行于x轴．若，则k的值为________．
【答案】6
【分析】由等腰三角形的性质可得，即点C的横坐标是点A横坐标的2倍，可设点A的坐标，进而得出点C的坐标，由点A、点C的纵坐标得出，进而利用全等三角形得出点E的横坐标为，利用反比例函数图象上点的坐标特征得出点E的纵坐标，再利用三角形的面积可得k的值．
【解析】解：如图，过点A作轴，交于点F，垂足为M，过点C作轴，垂足为N，
∵，
∴，
由于点A、点C在反比例函数的图象上，
可设点，即，，
∴，
∴点，即，
∴，
∴，
在和中，
，
∴，
∴，
∴点E的横坐标为，
又∵点E在反比例函数的图象上，
∴点E的纵坐标为，
即，
∵，即，
∴，
∴，
故答案为：6．
【点睛】本题考查反比例函数图象上点的坐标特征，以及一次函数与反比例函数的交点坐标，利用坐标表示线段的长是解决问题的关键．
27．（浙江省丽水市2021-2022学年八年级下学期期末数学试题）如图，以，为边长的矩形面积为，以为边长的正方形面积为，已知．
（1）当时，则的值是______；
（2）若为整数，，则矩形和正方形的周长之和的值是______．
【答案】 2 28或6+6
【分析】根据矩形与正方形的面积公式可得S1＝ab，S2＝c2，代入S1+4S2＝32，得出ab+4c2＝32．
（1）将a＝b＝2c代入ab+4c2＝32，解方程即可求出c的值；
（2）由2a﹣b+4＝0可得b＝2a+4．代入ab+4c2＝32，变形得出c2＝，根据c为整数，求出c可能为2或1．再求出a的值，进而得到矩形和正方形的周长之和．
【解析】解：由题意可得S1＝ab，S2＝c2，
∵S1+4S2＝32，
∴ab+4c2＝32．
（1）当a＝b＝2c时，
4c2+4c2＝32，
解得c＝±2（负值舍去），
即c＝2．
故答案为：2；
（2）∵2a﹣b+4＝0，
∴b＝2a+4．
∴S1+4S2＝ab+4c2＝a（2a+4）+4c2＝2a2+4a+4c2＝32，
∴a2+2a+2c2＝16，
∴c2＝，
∵c为整数，
∴c2可能取值有：4或1，
∴c可能为2或1．
当c＝2时，解得a＝2（负根舍去）；
当c＝1时，解得a＝﹣1（负根舍去），
∴矩形和正方形的周长之和为：
2a+2b+4c＝2a+2（2a+4）+4c＝6a+8+4c．
当c＝2，a＝2时，6a+8+4c＝6×2+8+4×2＝28；
当c＝1，a＝﹣1时，6a+8+4c＝6×（﹣1）+8+4×1＝6+6．
故答案为：28或6+6．
【点睛】本题考查了整式的加减，矩形与正方形的面积、周长公式，解一元二次方程，不等式的性质．掌握运算法则是解题的关键．
28．（2022春·浙江舟山·八年级统考期末）已知函数y=x+1的图象与x轴、y轴分别交于点C、B，与双曲线y交于点A、D．若AB+CD=BC，则k的值为 _____．
【答案】/0.75
【分析】分类讨论k的正负性是否符合题意，得出k大于0时符合题意，则先求出点C、B坐标，设点A的坐标是(m，n)，过点A作AEx轴于E点，根据相似三角形的性质和轴对称的性质得出关于m、n的方程即可求解．
【解析】解：当时， ，不符合题意；
当时由题意可知符合题意，
已知函数y=x+1的图像与x轴、y轴分别交于点C、B，
把x=0代入，y=1；y=0代入，x=-1；
∴B、C的坐标分别是(0，1)、(−1，0)，
∴OB=1，OC=1，BC=，
设点A的坐标是(m，n)，过点A作AE⊥x轴于E点，
∵AEOB，
∴△CBO∽△CAE，
∴，
函数y=x+1的图像与函数y=的图像都关于直线y=−x对称，
由对称性可得AB=CD，
又∵AB+CD=BC，
∴BC=2AB=2CD，AC=3AB
∴=，即，
解得m=，n=，
∴点A的坐标是，
∵点A在双曲线y=上，
∴k= ×=，
故答案为：．
【点睛】本题主要考查了反比例函数的解析式、相似三角形的判定与性质等知识点，将距离问题转化为求点的坐标的问题成为解答本题的关键．
29．（2022春·浙江台州·八年级统考期末）小明同学学习了菱形的知识后，结合之前学习的赵爽弦图，编了一个菱形版“赵爽弦图”．如图，菱形ABCD中，∠ABC=60°，四边形EFGH是矩形，若FA=FB=2，则矩形EFGH的面积为______．
【答案】/
【分析】过点A作AM⊥BC于M，过点G作GN⊥BC于N，连接GM，由FA=FB=2可得AB=4，∠ABF=∠BAF=45°，根据菱形的性质和矩形的性质可得∠CBG=15°，∠DAF=75°，则∠CDH=∠DCH=45°，∠ADE=15°，∠BCG=75°，可得出△ABF≌△CDH，△BCG≌△DAE，分别求出菱形ABCD，△ABF，△BCG的面积，即可得矩形EFGH的面积．
【解析】解：过点A作AM⊥BC于M，过点G作GN⊥BC于N，连接GM，
∵四边形EFGH是矩形，
∴∠AFB=∠AED=∠BGC=∠CHD=90°，
∵FA=FB=2，
∴AB==4，∠ABF=∠BAF=45°，
∵四边形ABCD是菱形，∠ABC=60°，
∴AB=BC=CD=AD，∠ABC=∠ADC=60°，∠BAD=∠BCD=120°，
∴∠CBG=15°，∠DAF=75°，
∴∠CDH=∠DCH=45°，∠ADE=15°，∠BCG=75°，
∴∠BAF=∠DCH=∠ABF=∠CDH，∠ADE=∠CBG，∠DAE=∠BCG，
在△ABF和△CDH中，
，
∴△ABF≌△CDH（ASA），
同理：△BCG≌△DAE（ASA），
∵AM⊥BC，∠ABC=60°，
∴∠BAM=30°，
∴BM=AB=2，
∴AM=BM=2，BC=2BM，
∵∠BGC=90°，
∴BM=CM=GM=2，
∴∠CMG=2∠CBG=30°，
∵GN⊥BC，
∴GN=GM=1，
∴S菱形ABCD=BC•AM=4×2=8，
S△ABF=AF•BF=×2×2=4，
S△BCG=BC•GN=×4×1=2，
∴S矩形EFGH=S菱形ABCD-2S△ABF-2S△BCG=8-12．
故答案为：8-12．
【点睛】本题考查的是菱形的性质，矩形的性质，全等三角形的判定与性质，直角三角形的性质，面积的计算，熟练掌握全等三角形的判定定理以及菱形的性质是解答本题的关键．
30．（2022春·浙江绍兴·八年级统考期末）如图，正方形ABCD边长为2，点E，F是对角线AC上的动点，且EF长度为1，连结BE，BF，则△BEF周长的最小值为______．
【答案】4
【分析】如图作，使得BH=EF=1，连接DH交BD由E，则△BEF的周长最小，利用勾股定理即可求解．
【解析】解：如图作，使得BH=EF=1，连接DH交AC由E，则△BEF的周长最小．
∵BH=EF=1，，
∴四边形EFBH是平行四边形，
∴BF=EH，
∵EB=ED，
∴BE+BF=EH+ED=DH，
∵四边形ABCD是正方形，
∴AC⊥BD，
∵，
∴BD⊥BH，
∴∠DBH=90°，
在Rt△DBH中，DH==3，
∴△BEF的周长的最小值为3+1=4．
故答案为：4．
【点睛】本题考查轴对称-最短问题，正方形的性质、勾股定理、平行四边形的判定和性质等知识，解题的关键是学会利用轴对称解决最短问题．
31．（2022春·浙江湖州·八年级统考期末）如图，在矩形ABCD中，AB＝2，AD＝，M为对角线BD所在直线的一个动点，点N是平面上一点．若四边形MCND为平行四边形，MN＝，则BM的值为 _____．
【答案】6或1
【分析】分两种情况：①如图1，M在对角线BD上时，设四边形MCND对角线MN和DC交于O，过O作OG⊥BD于G；②如图2，M在BD的延长线上时，过O作OG⊥BD于G；设BM＝x，表示MG的长，先根据直角三角形30度角的性质可得OG和DG的长，在直角三角形OGM中列方程可得结论．
【解析】解：分两种情况：
①如图1，M在对角线BD上时，设四边形MCND对角线MN和DC交于O，过O作OG⊥BD于G，
∵四边形MCND为平行四边形，
∴ODDCAB＝1，OMMN，
∵四边形ABCD是矩形，
∴∠A＝90°，
∵AB＝2，AD＝2，
∴BD4，
∴ABBD，
∴∠ADB＝30°，
∵∠ADC＝90°，
∴∠BDC＝60°，
Rt△ODG中，∠DOG＝30°，
∴DG，OG，
设BM＝x，则MG＝4﹣xx，
△OMG中，MG2+OG2＝OM2，
∴，
解得：x＝6（舍）或1；
②如图2，M在BD的延长线上时，过O作OG⊥BD于G，
同理得：DG，OG，OM，
设BM＝x，则MG＝x﹣4x，
在△OMG中，MG2+OG2＝OM2，
∴，解得：x＝6或1（舍）；
综上所述，BM的长为6或1，
故答案为：6或1．
【点睛】本题考查了矩形性质，平行四边形的判定，勾股定理等知识；熟练掌握矩形的性质，设未知数列方程是解决问题的关键．
32．（2022春·浙江金华·八年级统考期末）如图，矩形中，点，，分别在，，边上，，，平分，，则线段的长为______，线段的长为______．
【答案】 2 6
【分析】根据BE平分得，用ASA即可证明，即可得EF=EG，根据矩形的性质得，根据角之间的关系得，用AAS可证，即可得DF=CE=2，CG=DE=1，根据BF=BG和勾股定理得，，进行就是即可得．
【解析】解：∵BE平分，
∴，
在和中，
∴（ASA），
∴EF=EG，
∵四边形ABCD是矩形，
∴，，
∵，
∴，
∴，
∵，
∴，
在和中，
∴（AAS），
∴DF=CE=2，CG=DE=1，
设，则，，
∵BF=BG，
∴，
即
解得，，
即，
故答案为：2，6．
【点睛】本题考查了矩形的性质，勾股定理，全等三角形的判定与性质，解题的关键是掌握这些知识点．
33．（2022春·浙江湖州·八年级统考期末）如图，在平面直角坐标系中，已知，C为线段的中点，点P是线段上的一个动点，连接，当的值为____________时，将沿边所在直线翻折后得到的与重叠部分的面积为面积的．
【答案】
【分析】根据题意作出图形，根据与重叠部分的面积为面积的，得出为的中点，可得四边形为平行四边形，根据折叠的性质可得，即可求解．
【解析】解：，
，
如图，作关于的对称点，连接，，取的中点，
C为线段的中点，
，
为与重叠部分，
，
与重叠部分的面积为面积的，
过点，
对称，
，
与重叠部分的面积为面积的，
，
，
，
四边形为平行四边形，
，
对称，
，
．
故答案为：．
【点睛】本题考查了折叠的性质，勾股定理，平行四边形的性质与判定，三角形中线的性质，证明四边形为平行四边形是解题的关键．
34．（2022春·浙江宁波·八年级统考期末）如图，正方形ABCD边长为2，F为对角线AC上的一个动点，过C作AC的垂线并截取，连接EF，周长的最小值为______．
【答案】
【分析】先过作交于，再连接、，证四边形为矩形，得，据此知，再求出，当时，取得最小值，此时，从而得出答案．
【解析】解：如图，过作交于，连接、，
，，
，
，
，
，
，，
，
四边形为平行四边形，
，
四边形为矩形，
，
，
在中，，
，
当时，取得最小值，此时，
周长的最小值，
故答案为：．
【点睛】本题主要考查轴对称最短路线问题及矩形的判定与性质，正方形的性质，解题的关键是掌握矩形的判定与性质及轴对称的性质．
35．（2022春·浙江宁波·八年级统考期末）如图，点是内一点，轴，轴，，，，若反比例函数的图像经过、两点，则的值是______．
【答案】
【分析】根据三角形面积公式求得，易证得≌，得出，根据题意得出是等腰直角三角形，得出，设，则有D根据反比例函数的定义得出关于的方程，解方程求得，即可求得．
【解析】解：作轴于，延长，交于，设与轴的交点为，
四边形是平行四边形，
，，
，
轴，
，
，
与轴平行，与轴平行，
，，
，
≌（AAS），
，
，
，
，
，
是等腰直角三角形，
，
的纵坐标为，
设，则，
反比例函数的图像经过、两点，
，
解得：，
．
故答案为：．
【点睛】本题考查了反比例函数图像上点的坐标特征，平行四边形的性质，等腰直角三角形的判定和性质，三角形的面积等，表示出、的坐标是解题的关键．
36．（2022春·浙江金华·八年级统考期末）如图，在矩形ABCD中，，射线AE与BC边交于点E，点F是射线AE上的一点，点G在边AB上，以FG为边向上作菱形FGMN，若，当点G从点B运动到点A时，点N的运动路径长是_______．
【答案】3
【分析】如图，将线段绕点顺时针旋转得到，连接．证明，推出，推出点在射线上运动，推出当点从运动到时，．
【解析】解：如图，将线段绕点顺时针旋转得到，连接．
四边形是菱形，
，，
，
，
，
，
在和中，
，
（SAS），
，
点在射线上运动，
当点从运动到时，，
点的运动路径的长为3．
故答案为3．
【点睛】本题考查轨迹，全等三角形的判定和性质，菱形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．
37．（2022春·浙江温州·八年级统考期末）如图1是第32届夏季奥运会的会徽，它是由三种不同规格的全等矩形组成，代表了不同的国家、文化和思维方式，表达了多样性的融合．图2和图3为该会徽中的某一部分，如图2，三种矩形分别由三种不同的菱形依次连结各边中点得到，其中，．如图3，点恰好在的延长线上，则______度．若，则点，之间的距离为______．
【答案】 30
【分析】利用已知条件求出∠BOC的度数，利用三角形的内角和定理可求出∠OCB的度数；然后结合图3和图2，可得到∠IHE的度数；利用等腰三角形的性质及三角形的内角和定理求出∠MBT，∠TBM的度数，抽象图形，过点M作MJ⊥BT于点J，利用30°角所对的直角边等于斜边的一半，可求出MJ的长，利用勾股定理求出TJ的长，从而可求出BJ的长；在Rt△BMJ中利用勾股定理求出BM的长，即可得到EG的长；过点E作ES⊥EG于点E，交FG于点S，根据点D恰好在FE的延长线上，可求出∠FEG和∠EFS的度数，利用三角形的内角和定理求出∠G的度数，同时可证得SF=ES，利用直角三角形的性质求出SG的长；利用勾股定理求出SF的长；然后根据FG=SF+SG，代入计算求出FG的长．
【解析】解：∵∠BOC=360°-120°-90°=150°，
∴∠OCB=（180°-∠BOC）÷2=（180°-150°）÷2=15°，
∴∠IHE=2∠OCB=2×15°=30°；
∵如图2，三种矩形分别由三种不同的菱形依次连结各边中点得到，OA=1，
∴萎形的边长为2，
∴BT=MT=1，∠MBT=∠TBM=180°-90°-15°=75°，
过点M作MJ⊥BT于点J，
∴∠MJT=90°，∠T=30°，
∴
∴
∴BJ=BT-TJ=
在Rt△BMJ中，
∴
过点E作ES⊥EG于点E，交FG于点S，
∵点D恰好在FE的延长线上，
∴∠FEG=360°-90°-90°-75°=105°，∠EFS=15°，
∴∠G=180°-105°-15°=60°，
∴∠ESG=90°-60°=30°=∠F+∠FES，
∴∠F=∠FES=15°，
∴SF=ES，
∴
∴，
故答案为：30，
【点睛】本题考查了矩形的性质，菱形的性质，含30度角的直角三角形的性质，勾股定理，正确的计算是解题的关键．
38．（2022春·浙江杭州·八年级统考期末）如图是一张矩形纸片ABCD，点E在AC边上，把△DCE沿直线DE折叠，使点C落在对角线BD上的点F处；点G在AB边上，把△DAG沿直线DG折叠，使点A落在线段DF上的点H处．若HF＝1，BF＝8，则BD＝______，矩形ABCD的面积＝______．
【答案】 29 420
【分析】由折叠的性质得HD=AD，FD=CD，设AD=x，则HD=x，得AB=CD=x+1，BD=x+9，再在Rt△ABD中，由勾股定理得出方程，解方程，即可解决问题．
【解析】解：∵四边形ABCD是矩形，
∴AB=CD，∠A=90°，
由折叠的性质得：HD=AD，FD=CD，
设AD=x，则HD=x，
∴AB=CD=FD=HD+HF=x+1，
∴BD=FD+BF=x+9，
在Rt△ABD中，由勾股定理得：x2+（x+1）2=（x+9）2，
解得：x=20或x=-4（舍去），
∴AD=20，AB=21，BD=x+9=29，
∴矩形ABCD的面积=AD•AB=20×21=420，
故答案为：29，420．
【点睛】本题考查了翻折变换的性质、矩形的性质以及勾股定理等知识，熟练掌握翻折变换的性质和矩形的性质，由勾股定理得出方程是解题的关键．
39．（2022春·浙江·八年级统考期末）如图，在矩形ABCD中，将矩形ABCD沿EF折叠，点A落在点处，点B落在CD边点处，连结B交EF于点G，点M在上，M=2M，若CD=3，AD=6，在折叠的过程中，点在边CD上不同的位置时，则MG+G的最小值为______．
【答案】
【分析】在AB上取点H，使得AH＝2BH，根据折叠的性质可得GH＝GM，GB＝GB′，根据直角三角形的性质得出GB＝GC＝GB′，可得当H、G、C三点共线时，MG+G有最小值，利用勾股定理求出最小值HC即可．
【解析】解：如图，在AB上取点H，使得AH＝2BH，
由折叠可知四边形ABFE与四边形A′B′FE关于直线EF对称，
∵AH＝2BH，M=2M，
∴GH＝GM，GB＝GB′，
∵∠BCD＝90°，
∴GB＝GC＝GB′，
∴MG+G＝GH+GC，
∴当H、G、C三点共线时，MG+G有最小值，
∵在矩形ABCD中，CD=3，AD=6，
∴BH＝1，BC＝6，
∴最小值为HC＝，
故答案为：．
【点睛】本题考查了矩形的性质，折叠的性质，直角三角形的性质以及勾股定理等，分析得出当H、G、C三点共线时，MG+G有最小值是解答此题的关键．