浙教版八年级数学下册期中期末挑战满分冲刺卷特训14期末解答题汇编46道(浙江精选归纳)(原卷版+解析)

这是一份浙教版八年级数学下册期中期末挑战满分冲刺卷特训14期末解答题汇编46道(浙江精选归纳)(原卷版+解析)，共64页。试卷主要包含了解答题等内容，欢迎下载使用。
1．（2023春·浙江·八年级专题练习）计算：
(1)；
(2)．
2．（2022秋·浙江宁波·八年级统考期末）计算：
(1)×÷；
(2)（﹣）×；
(3)．
3．（2022秋·浙江宁波·八年级校考期末）（1）解方程：
（2）计算：
4．（2022秋·浙江杭州·八年级杭州外国语学校校考期末）化简或解方程：
(1)÷﹣84；
(2)＋（）2；
(3)3x2﹣2＝4x；
(4)（2x＋3）2＝2（2x＋3）．
5．（2022秋·浙江宁波·八年级统考期末）解方程：
(1)；
(2)；
(3)．
6．（2022春·浙江金华·八年级统考期末）解方程：
(1)
(2)
7．（2023春·浙江衢州·八年级校考阶段练习）请选择适当的方法解下列一元二次方程：
(1)
(2)
(3)
(4)
8．（2023春·浙江衢州·八年级校考阶段练习）已知关于x的方程．
(1)求证：无论m为何值，方程总有两个不相等的实数根；
(2)若方程根的判别式的值为5，求m的值及方程的根．
9．（2021春·浙江杭州·八年级期末）已知关于的一元二次方程：．
(1)求证：这个方程总有两个实数根．
(2)若等腰的一边长，另两边b、c恰好是这个方程的两个实数根，求的周长．
10．（2022春·浙江绍兴·八年级统考期末）已知关于x的方程．
(1)求证：无论m取什么实数，这个方程总有两个不相等的实数根．
(2)若这个方程的两个实根，，满足，求m的值．
11．（2021春·浙江·八年级期末）已知x1，x2是关于x的一元二次方程x2﹣2（m＋1）x＋m2＋5＝0的两实数根．
(1)若（x1﹣1）（x2﹣1）＝28，求m的值；
(2)已知等腰△ABC的一边长为7，若x1，x2恰好是△ABC另外两边的边长，求这个三角形的周长．
12．（2020春·浙江杭州·八年级期末）已知：关于x的方程kx2﹣（4k﹣3）x＋3k﹣3＝0
(1)求证：无论k取何值，方程都有实根；
(2)若x＝﹣1是该方程的一个根，求k的值；
(3)若方程的两个实根均为正整数，求k的值（k为整数）．
13．（2021春·浙江·八年级期末）完成下列各小题：
（1）已如，求的值；
（2）已知，求式子的值；
14．（2020秋·浙江·八年级期末）求值：
（1）若，，求的值；
（2）若的整数部分为a，小数部分为b，求的值．
15．（2023春·浙江·八年级专题练习）已知．
(1)求的值；
(2)求的值．
16．（2023春·浙江·八年级专题练习）【阅读材料】小明在学习二次根式时，发现一些含根号的式子可以化成另一个式子的平方，
如：，
；
【类比归纳】
(1)请你仿照小明的方法将化成另一个式子的平方．
【变式探究】
(2)若且a，m，n均为正整数，求a值．
17．（2023秋·浙江宁波·八年级校考期末）下表是小明这一学期数学成绩测试记录，根据表格提供的信息，回答下列问题：
(1)求小明6次成绩的众数与中位数；
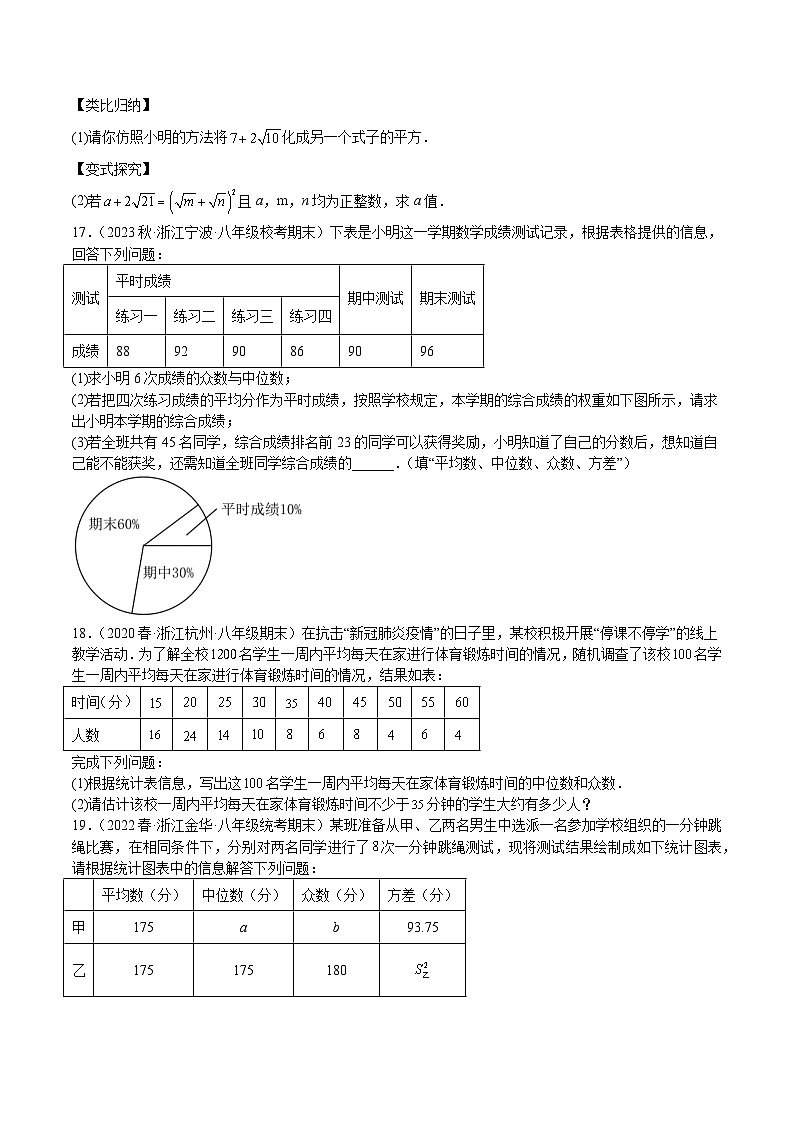
(2)若把四次练习成绩的平均分作为平时成绩，按照学校规定，本学期的综合成绩的权重如下图所示，请求出小明本学期的综合成绩；
(3)若全班共有45名同学，综合成绩排名前23的同学可以获得奖励，小明知道了自己的分数后，想知道自己能不能获奖，还需知道全班同学综合成绩的______．（填“平均数、中位数、众数、方差”）
18．（2020春·浙江杭州·八年级期末）在抗击“新冠肺炎疫情”的日子里，某校积极开展“停课不停学”的线上教学活动．为了解全校名学生一周内平均每天在家进行体育锻炼时间的情况，随机调查了该校名学生一周内平均每天在家进行体育锻炼时间的情况，结果如表：
完成下列问题：
(1)根据统计表信息，写出这名学生一周内平均每天在家体育锻炼时间的中位数和众数．
(2)请估计该校一周内平均每天在家体育锻炼时间不少于分钟的学生大约有多少人？
19．（2022春·浙江金华·八年级统考期末）某班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛，在相同条件下，分别对两名同学进行了次一分钟跳绳测试，现将测试结果绘制成如下统计图表，请根据统计图表中的信息解答下列问题：
(1)表中______；______．
(2)求出乙得分的方差．
(3)根据已有的信息，你认为应选谁参赛较好，请说明理由．
20．（2022春·浙江舟山·八年级校联考期末）某中学九年级组织了一次数学计算比赛（禁用计算器），每班选25名同学参加比赛，成绩分为A，B，C，D四个等级，其中A等级得分为100分，B等级得分为85分，C等级得分为75分，D等级得分为60分，数学教研组将九年级一班和二班的成绩整理并绘制成如下的统计图，请根据提供的信息解答下列问题．
(1)把一班竞赛成绩统计图补充完整．
(2)填表：
(3)请从以下给出的两个方面对这次比赛成绩的结果进行分析：
①从平均数、众数方面来比较一班和二班的成绩；
②从B级以上（包括B级）的人数方面来比较一班和二班的成绩．
21．（2022春·浙江台州·八年级统考期末）学校餐厅对某天中午的三个套餐的满意度进行调研，随机选取了部分学生，对A，B，C三个套餐的色、香、味三个方面分别进行评分（各项评分60-100分，评分均为整数），并按照色、香、味3∶3∶4的比例计算综合得分，将数据进行整理、描述后得到下列信息：
信息一：学生小张对三个套餐各项评分（单位：分）
信息二：三个套餐综合得分x在各分数段的人数比例分布图
根据以上信息，回答下列问题：
(1)根据信息一：求小张对套餐A的评分的综合得分；
(2)根据信息二：套餐B的综合得分的中位数位于_______分数段；试估计该学校餐厅______套餐综合得分不低于90分人数最多；
(3)若套餐A综合得分高于小张评分的人数有a人，套餐C的综合得分高于小张评分（综合得分为79.8）的有b人，试比较a和b的大小，并说明理由．
22．（2022春·浙江绍兴·八年级统考期末）请根据图片内容，回答下列问题：
(1)每轮传染中，平均一个人传染了几个人？
(2)按照这样的速度传染，第三轮将新增多少名感染者（假设每轮传染人数相同）？
23．（2019春·浙江金华·八年级统考期末）社区利用一块矩形空地建了一个小型的惠民停车场，其布局如图所示，已知停车场的长为52米，宽为28米，阴影部分设计为停车区，要铺花砖，其余部分是通道，且宽度相等．已知铺花砖的面积为640平方米．
(1)求通道的宽是多少米？
(2)该停车场共有车位64个，据调查分析，当每个车位的月租金为200元时，可全部租出；当每个车位的月租金每上涨10元，就会少租出1个车位．为了维护消费者利益，物价部门规定，每个车位租金不得超过500元，要想让停车场的月租金收入为14400元，每个车位的月租金应上涨多少元？
24．（2021春·浙江·八年级期末）今年超市以每件25元的进价购进一批商品，当商品售价为40元时，三月份销售256件，四、五月该商品十分畅销，销售量持续上涨，在售价不变的基础上，五月份的销售量达到400件．
(1)求四、五这两个月销售量的月平均增长百分率．
(2)经市场预测，六月份的销售量将与五月份持平，现商场为了减少库存，采用降价促销方式，经调查发现，该商品每降价1元，月销量增加5件，当商品降价多少元时，商场六月份可获利4250元？
25．（2023春·浙江温州·八年级统考期中）有一块长为米，宽为米的长方形场地，计划在该场地上修建宽均为x米的两条互相垂直的道路，余下的四块长方形场地建成草坪．
(1)已知，，且四块草坪的面积和为平方米，则每条道路的宽为多少米？
(2)若，，且四块草坪的面积和为平方米，则原来矩形场地的长和宽各为多少米？
(3)已知，，现要在场地上修建若干条宽均为米的纵横小路，假设有条水平方向的小路，条竖直方向的小路(其中n为常数)，使草坪地的总面积为平方米，则 (直接写出答案)．
26．（2022春·浙江杭州·八年级统考期末）某小区计划用40米的篱笆围一个矩形花坛，其中一边靠墙（墙足够长，篱笆要全部用完）．
(1)如图1，问为多少米时，矩形的面积为200平方米？
(2)如图2，矩形的面积比（1）中的矩形面积减小20平方米，小明认为只要此时矩形的长比图①中矩形的长少2米就可以了．请你通过计算，判断小明的想法是否正确．
27．（2022春·浙江湖州·八年级统考期末）奥运会是各个国家彰显国家实力的舞台．2022年冬季奥运会和冬季残奥会两件赛事在我国首都北京和河北省石家庄市举行．本次运动会的两个可爱的吉祥物“冰墩墩”和“雪容融”以满满的“未来感”和“中国风”圈粉无数．某商家购进了两种类型的冬奥吉祥物纪念品，两次购进纪念品的情况如下表：
(1)求两种类型的纪念品每个进价各是多少元？
(2)在销售过程中，“冰墩墩”类纪念品因为物美价廉而更受消费者喜欢．为了增大“雪容融”类纪念品的销售量，商家决定对“雪容融”类纪念品进行降价销售，当销售价为每个44元时，每天可以售出20个，每降价1元，每天将多售出5个．请问商家应将“雪容融”类纪念品每个降价多少元时，每天售出此类纪念品能获利400元？
28．（2021春·浙江嘉兴·八年级统考期末）如图1，将一块形状为矩形的空地ABCD修建成一个花圃，其中AB=12米，BC=20米．设计方案为：该花圃由一条宽度相等的环形小道（图2中阴影）和花卉种植区域（图2中矩形EFGH）组成．
（1）若环形小道面积是花圃面积的，求小道的宽度．
（2）若花卉种植区域分割成如图3的形状，点I，J，K分别在边EH，EF，FG上，L为花圃内一点，四边形HIJL和四边形GLJK均为平行四边形．已知KG的长是小道宽度的2倍，且四边形HIJL与四边形GLJK的面积之和是花圃面积的，求小道的宽度．
29．（2021春·浙江温州·八年级统考期末）用总长的木板制作矩形置物架（如图），已知该置物架上面部分为正方形，下面部分是两个全等的矩形和矩形，中间部分为矩形．已知，设正方形的边长
（1）当时，的长为______．
（2）置物架的高的长为 （用含的代数式表示）．
（3）为了便于置放物品，的高度不小于，若矩形的面积为，求的值．
30．（2020春·浙江杭州·八年级期末）如图，在中，，，垂足分别为，，求证：四边形是平行四边形．
31．（2020春·浙江杭州·八年级期末）如图，在中，分别是和的角平分线，已知．
(1)求线段的长；
(2)延长 ，交的延长线于点．
请在答卷上补全图形；
若，求的周长．
32．（2022春·浙江金华·八年级统考期末）如图，在平行四边形中，点、分别为，的中点，点，在对角线上，且．
(1)求证：四边形是平行四边形．
(2)如图，连交于点，若，，求的长．
33．（2022春·浙江湖州·八年级统考期末）在的菱形网格中，点A，B，C都在格点上，仅用无刻度的直尺，按要求画图：
(1)在图1中找一个格点D，使得以A，B，C，D为顶点的四边形是平行四边形；
(2)在图2中作中平行于边的中位线．（保留画图痕迹，不写画法）
34．（2022春·浙江丽水·八年级统考期末）如图，在菱形中，E为对角线上一点，连接．
(1)求证：；
(2)若，求的度数．
35．（2019春·浙江绍兴·八年级统考期末）如图，矩形中，点E、F分别在边、上，且．
(1)求证：四边形是平行四边形．
(2)若四边形是菱形，，，求菱形的周长．
36．（2022春·浙江杭州·八年级校考期末）如图，在四边形中，，，的平分线交于点，连接．
(1)求证：四边形是菱形；
(2)若，，求的长．
37．（2022春·浙江杭州·八年级统考期末）已知：如图，在菱形中，为对角线，是上的点，分别连结，并延长交于点，交于点．
(1)求证：；
(2)若，，，求的长．
38．（2022春·浙江舟山·八年级校联考期末）如图，在正方形ABCD中，E、F分别为边AB、BC的中点，连接AF、DE交于点G，连结BG．
(1)试判断AF与DE的数量关系与位置关系，并证明．
(2)求证：BG平分∠EGF．
39．（2022春·浙江宁波·八年级校联考期末）正方形中，对角线、交于点，为上一点，延长到点，使，连接、．
(1)求证：．
(2)求证：为直角三角形．
(3)若，正方形的边长为，求的长．
40．（2017春·浙江·八年级统考期末）如图，在平面直角坐标系中，直线与x轴交于点A，与双曲线在第二象限内交于点．
(1)求a和b的值；
(2)过点B作直线l平行x轴交y轴于点C，连接，求的面积．
41．（2022春·浙江湖州·八年级统考期末）如图，已知是一次函数和反比例函数的图象的两个交点，直线与y轴交于点C．求：
(1)反比例函数和一次函数的解析式；
(2)不等式的解集（直接写出答案）．
42．（2022春·浙江杭州·八年级统考期末）已知点， 都在反比例函数的图象上．
(1)当时
①求反比例函数表达式，并求出点的坐标；
②当时，求的取值范围．
(2)若一次函数与轴交于点，求的值．
43．（2022春·浙江宁波·八年级统考期末）在平面直角坐标系中，一次函数的图象与反比例函数图象交于A、B两点，其中A点坐标为．
(1)分别求出k、m的值．
(2)求B点的坐标．
(3)根据图象，直接写出不等式的解集．
44．（2021春·浙江宁波·八年级统考期末）为预防传染病，某校定期对教室进行“药熏消毒”，如图，药物燃烧阶段，室内每立方米空气中的含药量y（毫克）与燃烧时间x（分）成正比例，10分钟时药物燃尽，此时教室内每立方米空气含药量为8毫克，燃尽后y与x成反比例．
(1)求第5分钟时教室内每立方米空气中的含药量；
(2)画出药物燃尽后y关于x的反比例函数图象；
(3)当每立方米空气中含药量低于1.6毫克时，对人体方能无毒害作用，那么从消毒开始，在哪个时段学生不能停留在教室里？
45．（2023春·浙江·八年级期末）边长为1的8个正方形如图摆放在直角坐标系中，直线平分这8个正方形所组成的图形的面积，交其中两个正方形的边于A，B两点，过点B的反比例函数的图象的一支交其中两个正方形的边于C，D两点，另一支交直线于点E，连接OC，OD，CD，
(1)求k1，k2的值；
(2)求的面积；
(3)过原点O的另一条直线交反比例函数的图象于P，Q两点（P点在第一象限），若由点B，E，P，Q为顶点的四边形的面积为12，求点P的横坐标．（直接写出答案）
46．（2023春·浙江·八年级期末）定义：只有三边相等的四边形称为准菱形．
（1）如图1，图形 （填序号）是准菱形；
（2）如图2，四边形ABCD中，AB∥DC，∠B+∠D＝180°，AB＝AD，求证：四边形ABCD是准菱形；
（3）如图3，在平面直角坐标系xOy中，矩形OABC的边OA，OC分别落在y轴，x轴上，反比例函数y＝（k＞0）的图象分别与边AB，BC交于点D，E．已知AD＝DE，△ADE的面积为10，AD：DB＝5：3，若点F是坐标平面上一点，四边形ADEF是准菱形，当准菱形ADEF面积最大时，求点F的坐标．
测试
平时成绩
期中测试
期末测试
练习一
练习二
练习三
练习四
成绩
88
92
90
86
90
96
时间分
人数
平均数（分）
中位数（分）
众数（分）
方差（分）
甲
175
a
b
93.75
乙
175
175
180
平均数（分）
中位数（分）
众数（分）
一班
82.8


二班

75
100
套餐
色
香
味
A
72
90
80
B
68
76
92
C
88
82
72
进货批次
“冰墩墩”类纪念品（个）
“雪容融”类纪念品（个）
总费用（元）
一
100
200
8000
二
200
300
13000
特训14 期末解答题汇编46道（浙江精选归纳）
一、解答题
1．（2023春·浙江·八年级专题练习）计算：
(1)；
(2)．
【答案】(1)
(2)
【分析】（1）先把二次根式化为最简二次根式，然后合并即可；
（2）利用完全平方公式和平方差公式计算．
【解析】（1）解：
；
（2）解：
【点睛】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后合并同类二次根式即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．
2．（2022秋·浙江宁波·八年级统考期末）计算：
(1)×÷；
(2)（﹣）×；
(3)．
【答案】(1)
(2)
(3)
【分析】（1）根据二次根式的乘除法计算，然后化成最简式子即可；
（2）先化简括号内的式子，然后计算括号外的乘法即可；
（3）先化简，然后合并同类二次根式即可．
【解析】（1）×÷
=
=
=4；
（2）()
=(3）
=6﹣6；
（3）
．
【点睛】本题主要考查二次根式的运算，熟练掌握二次根式的运算法则是解题的关键．
3．（2022秋·浙江宁波·八年级校考期末）（1）解方程：
（2）计算：
【答案】（1），（2）
【分析】（1）利用因式分解法求解；
（2）先利用二次根式的性质化简，再合并同类项．
【解析】解：（1），
移项，得，
等号左边提取公因式，得，
即，
因此或，
解得；
（2）原式
．
【点睛】本题考查因式分解法解一元二次方程、二次根式的加减运算，解（1）的关键是掌握因式分解法解一元二次方程的步骤；解（2）的关键是掌握二次根式的性质．
4．（2022秋·浙江杭州·八年级杭州外国语学校校考期末）化简或解方程：
(1)÷﹣84；
(2)＋（）2；
(3)3x2﹣2＝4x；
(4)（2x＋3）2＝2（2x＋3）．
【答案】(1)
(2)
(3)，
(4)，
【分析】（1）根据二次根式混合运算的法则计算即可；
（2）利用完全平方公式和二次根式的除法法则运算．
（3）利用公式法求解即可；
（4）利用因式分解法求解即可．
(1)
原式
；
(2)
原式
；
(3)
，
，
△，
，
，
(4)
，
，
，
或，
，．
【点睛】此题考查了二次根式的混合运算，解一元二次方程，熟练掌握解一元二次方程的方法是解本题的关键．
5．（2022秋·浙江宁波·八年级统考期末）解方程：
(1)；
(2)；
(3)．
【答案】(1)；
(2)；
(3)．
【分析】（1）利用因式分解法求解即可得；
（2）整理后，直接开平方法解方程；
（3）利用公式法求解即可．
【解析】（1）解：∵，
∴，
∴或，
∴；
（2）解：∵，
∴，
∴，
∴，
∴；
（3）解：∵，
，
∴，
则，
即．
【点睛】此题主要考查解一元二次方程，熟练根据方程特点选择合适的方法是解题关键．
6．（2022春·浙江金华·八年级统考期末）解方程：
(1)
(2)
【答案】(1)，
(2)，
【分析】（1）利用因式分解法解方程即可；
（2）先移项得到，然后利用因式分解法解方程．
（1）
解：，
∴，
∴，；
（2）
解：移项得：，
因式分解得：，
∴，
∴3x=0或x+2=0，
∴，．
【点睛】本题考查了解一元二次方程-因式分解法：因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法，熟练掌握因式分解的方法是解题的关键．
7．（2023春·浙江衢州·八年级校考阶段练习）请选择适当的方法解下列一元二次方程：
(1)
(2)
(3)
(4)
【答案】(1)，；
(2)，；
(3)，；
(4)，
【分析】（1）利用直接开方法求解即可；
（2）利用因式分解法求解即可；
（3）利用公式法求解求解即可；
（4）利用因式分解法求解即可．
【解析】（1）解：
∴
直接开方得：或，
解得：，；
（2）
，
∴，
解得：，；
（3），
其中，
∴，
∴,，
∴，；
（4）
移项得：，
∴，
整理得：，
解得：，．
【点睛】题目主要考查解一元二次方程，熟练掌握解一元二次方程的方法步骤是解题关键．
8．（2023春·浙江衢州·八年级校考阶段练习）已知关于x的方程．
(1)求证：无论m为何值，方程总有两个不相等的实数根；
(2)若方程根的判别式的值为5，求m的值及方程的根．
【答案】(1)见解析
(2)或3，当时，方程的解为；当时，方程的解为；
【分析】（1）先得出一元二次方程根的判别式，再证明判别式大于0即可解答；
（2）令判别式等于5求得或3，然后分和两种情况，分别代入方程求解即可．
【解析】（1）证明：∵，
∴，
∴不论m为何值时，方程总有两个不相等的实数根．
（2）解：令，则，解得：或3
当时，原方程可化为：
∴
∴；
当时，原方程可化为：
∴
∴；
综上，当时，方程的解为；当时，方程的解为．
【点睛】本题主要考查一元二次方程根的判别式、解一元二次方程等知识点，由方程根的情况得到判别式的符号是解题的关键．
9．（2021春·浙江杭州·八年级期末）已知关于的一元二次方程：．
(1)求证：这个方程总有两个实数根．
(2)若等腰的一边长，另两边b、c恰好是这个方程的两个实数根，求的周长．
【答案】(1)见解析
(2)10
【分析】（1）先计算△，化简得到，易得，然后根据△的意义即可得到结论；
（2）利用求根公式计算出方程的两根，，则可设，，然后讨论：当、为腰；当、为腰，分别求出边长，但要满足三角形三边的关系，最后计算周长．
【解析】（1）解：证明：
，
无论取什么实数值，，
，
无论取什么实数值，方程总有实数根；
（2），
，，
，恰好是这个方程的两个实数根，设，，
当、为腰，则，即，解得，此时三角形的周长；
当、为腰时，，此时，故此种情况不存在．
综上所述，的周长为10．
【点睛】本题考查了一元二次方程的根的判别式：当，方程有两个不相等的实数根；当，方程有两个相等的实数根；当，方程没有实数根．也考查了三角形三边的关系以及分类讨论思想的运用．
10．（2022春·浙江绍兴·八年级统考期末）已知关于x的方程．
(1)求证：无论m取什么实数，这个方程总有两个不相等的实数根．
(2)若这个方程的两个实根，，满足，求m的值．
【答案】(1)证明见解析
(2)，
【分析】（1）△=＞0，无论m取什么实数，这个方程总有两个不相等的实数根；
（2）根据根与系数关系可得：，即可求解.
（1）
证明：∵，
无论m取何实数，的值都大于零．
∴这个方程总有两个不相等的实数根．
（2）
解：∵，是方程的两个实数根，
∴．
又∵，
∴．
∴，代入原方程得：
，
化简得：．
解得：，．
【点睛】本题考查了根的判别式及根与系数的关系、解一元二次方程，解题的关键是熟知根与系数的关系及用根的判别式判定根的情况．
11．（2021春·浙江·八年级期末）已知x1，x2是关于x的一元二次方程x2﹣2（m＋1）x＋m2＋5＝0的两实数根．
(1)若（x1﹣1）（x2﹣1）＝28，求m的值；
(2)已知等腰△ABC的一边长为7，若x1，x2恰好是△ABC另外两边的边长，求这个三角形的周长．
【答案】(1)6
(2)17
【分析】（1）根据一元二次方程的判别式与根的关系可得△≥0，解不等式即可得出m的取值范围，根据一元二次方程根与系数的关系可得出x1+x2和x1x2的值，代入可得关于m的方程，解方程求出m的值即可；
（2）分7为腰和底边两种情况，分别根据一元二次方程的解的定义及一元二次方程根的判别式求出m的值，可得出三角形的三边长，根据三角形的三边关系即可求出三角形的周长．
【解析】（1）∵关于x的一元二次方程有两实数根，
∴=4（m+1）2-4（m2+5）=8m-16≥0，
解得：m≥2．
∵x1，x2是关于x的一元二次方程的两实数根．
∴x1+x2=2（m+1），x1x2=m2+5，
∵（x1-1）（x2 -1）=28，即x1x2-（x1+x2）+1=28，
∴m2+5-2（m+1）+1=28，
整理得：m2-2m-24=0，解得m1=6，m2=-4，
∵m≥2，
∴m的值为6．
（2）①当7为腰时，则x1、x2中有一个为7，设x1=7，
把x1=7代入方程得：49-14（m+1）+m2+5=0，
整理得m2-14m+40=0，
解得m1=10，m2=4，
当m=10时，x1+x2=2（m+1）=22，
解得：x2=15，
∵7+7