2024年湖南省长沙市湖南师大附中联考九上数学开学达标检测试题【含答案】

这是一份2024年湖南省长沙市湖南师大附中联考九上数学开学达标检测试题【含答案】，共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分） “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b．若ab=8，大正方形的面积为25，则小正方形的边长为
A．9B．6C．4D．3
2、（4分）如图，矩形ABCD中，对角线AC，BD交于点O，E，F分别是边BC，AD的中点，AB＝2，BC＝4，一动点P从点B出发，沿着B﹣A﹣D﹣C在矩形的边上运动，运动到点C停止，点M为图1中某一定点，设点P运动的路程为x，△BPM的面积为y，表示y与x的函数关系的图象大致如图2所示．则点M的位置可能是图1中的（ ）
A．点CB．点OC．点ED．点F
3、（4分）已知：如图，折叠矩形ABCD，使点B落在对角线AC上的点F处，若BC＝8，AB＝6，则线段CE的长度是（ ）
A．3B．4C．5D．6
4、（4分）如图，平行四边形ABCD中，AB=8cm，AD=12cm，点P在AD 边上以每秒1cm的速度从点A向点D运动，点Q在BC边上，以每秒4cm的速度从点C出发，在CB间往返运动，两个点同时出发，当点P到达点D时停止(同时点Q也停止)，在运动以后，以P、D、Q、B四点组成平行四边形的次数有( )
A．4次B．3次C．2次D．1次
5、（4分）一个多边形的内角和是外角和的2倍，这个多边形是( )
A．四边形B．五边形C．六边形D．八边形
6、（4分）甲、乙、丙、丁四人进行100m短跑训练，统计近期10次测试的平均成绩都是13.2s，10次测试成绩的方差如下表则这四人中发挥最稳定的是（ ）
A．甲B．乙C．丙D．丁
7、（4分）如图,在平面直角坐标系中，点在坐标轴上，是的中点，四边形是矩形，四边形是正方形，若点的坐标为，则点的坐标为( )
A．B．C．D．
8、（4分）一组数据1，3，4，4，4，5，5，6的众数和方差分别是（ ）
A．4，1B．4，2C．5，1D．5，2
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）一元二次方程化成一般式为________.
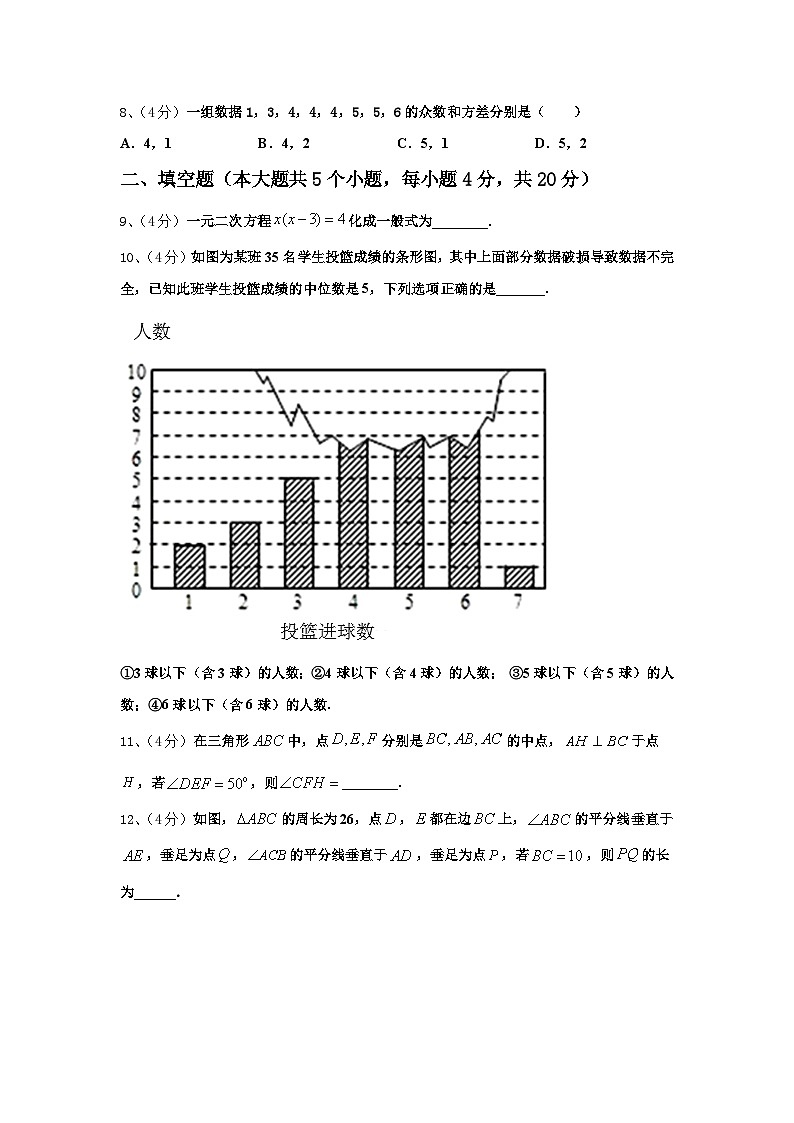
10、（4分）如图为某班35名学生投篮成绩的条形图，其中上面部分数据破损导致数据不完全，已知此班学生投篮成绩的中位数是5，下列选项正确的是_______.
①3球以下（含3球）的人数；②4球以下（含4球）的人数； ③5球以下（含5球）的人数；④6球以下（含6球）的人数.
11、（4分）在三角形中，点分别是的中点，于点，若，则________.
12、（4分）如图，的周长为26，点，都在边上，的平分线垂直于，垂足为点，的平分线垂直于，垂足为点，若，则的长为______.
13、（4分）命题”两条对角线相等的平行四边形是矩形“的逆命题是_____．
三、解答题（本大题共5个小题，共48分）
14、（12分）四边形为正方形，点为线段上一点，连接，过点作，交射线于点，以、为邻边作矩形，连接.
（1）如图，求证：矩形是正方形；
（2）当线段与正方形的某条边的夹角是时，求的度数.
15、（8分）如图分别是的网格，网格中每个小正方形的边长均为1，线段AB的端点在小正方形的顶点上，请在以下图中各画一个图形，所画图形各顶点必须在小正方形的顶点上，并且分别满足以下要求：
（1）在下图中画一个以线段AB为一边的直角，且的面积为2；
（2）在下图中画一个以线段AB为一边的四边形ABDE，使四边形ABDE是中心对称图形且四边形ABDE的面积为1．连接AD，请直接写出线段AD的长.线段AD的长是________
16、（8分）某校八年级全体同学参加了某项捐款活动，随机抽查了部分同学捐款的情况统计如图所示．

（1）本次共抽查学生 人，并将条形图补充完整；
（2）捐款金额的众数是 平均数是 中位数为
（3）在八年级600名学生中，捐款20元及以上（含20元）的学生估计有多少人？
17、（10分）如图，矩形ABCD中，AB＞AD，把矩形沿对角线AC所在直线折叠，使点B落在点E处，AE交CD于点F，连接DE，求证：∠DAE＝∠ECD．
18、（10分）如图，在边长为1个单位长度的小正方形组成的网格中，的顶点均在格点上，点A的坐标为，点B的坐标为，点C的坐标为.
（1）以点C为旋转中心，将旋转后得到，请画出；
（2）平移，使点A的对应点的坐标为，请画出;
（3）若将绕点P旋转可得到，则点P的坐标为___________.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）关于的x方程＝1的解是正数，则m的取值范围是_____．
20、（4分）八年级（3）班共有学生50人，如图是该班一次信息技术模拟测试成绩的频数分布直方图（满分为50分，成绩均为整数），若不低于30分为合格，则该班此次成绩达到合格的同学占全班人数的百分比是__________．
21、（4分）一次函数y=（2m﹣6）x+4中，y随x的增大而减小，则m的取值范围是_____．
22、（4分）当时，__．
23、（4分）如图，正方形ABCD中，AB=6，E是BC的中点，点P是对角线AC上一动点，则PE+PB的最小值为_____。
二、解答题（本大题共3个小题，共30分）
24、（8分）（1）（发现）如图1，在中，分别交于，交于．已知，，，求的值．
思考发现，过点作，交延长线于点，构造，经过推理和计算能够使问题得到解决（如图2）．
请回答：的值为______．
（2）（应用）如图3，在四边形中，，与不平行且，对角线，垂足为．若，，，求的长．
（3）（拓展）如图4，已知平行四边形和矩形，与交于点，，且，，判断与的数量关系并证明．
25、（10分）商场销售一批衬衫，平均每天可销售20件，每件盈利40元．为了扩大销售，增加盈利，尽量减少库存，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价5元，商场平均每天可多售出10件．求：
（1）若商场平均每天要盈利1200元，每件衬衫应降价多少元？
（2）要使商场平均每天盈利1600元，可能吗？请说明理由．
26、（12分）如图，在边长为的正方形ABCD中，作∠ACD的平分线交AD于F，过F作直线AC的垂线交AC于P，交CD的延长线于Q，又过P作AD的平行线与直线CF交于点E，连接DE，AE，PD，PB．
（1）求AC，DQ的长；
（2）四边形DFPE是菱形吗？为什么？
（3）探究线段DQ，DP，EF之间的数量关系，并证明探究结论；
（4）探究线段PB与AE之间的数量关系与位置关系，并证明探究结论．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
已知ab＝8可求出四个三角形的面积，用大正方形面积减去四个三角形的面积得到小正方形的面积，根据面积利用算术平方根求小正方形的边长.
【详解】




故选D.
本题考查勾股定理的推导，有较多变形题，解题的关键是找出图形间面积关系，同时熟练运用勾股定理以及完全平方公式，本题属于基础题型．
2、B
【解析】
从图2中可看出当x＝6时，此时△BPM的面积为0，说明点M一定在BD上，选项中只有点O在BD上，所以点M的位置可能是图1中的点O．
【详解】
解：∵AB＝2，BC＝4，四边形ABCD是矩形，
∴当x＝6时，点P到达D点，此时△BPM的面积为0，说明点M一定在BD上，
∴从选项中可得只有O点符合，所以点M的位置可能是图1中的点O．
故选：B．
本题主要考查了动点问题的函数图象，解题的关键是找出当x＝6时，此时△BPM的面积为0，说明点M一定在BD上这一信息．
3、C
【解析】
在Rt△ABC中利用勾股定理可求出AC＝1，设BE＝a，则CE＝8﹣a，根据折叠的性质可得出BE＝FE＝a，AF＝AB＝6，∠AFE＝∠B＝90°，进而可得出FC＝2，在Rt△CEF中，利用勾股定理可得出关于a的一元二次方程，解之即可得出a值，将其代入8﹣a中即可得出线段CE的长度．
【详解】
解：在Rt△ABC中，AB＝6，BC＝8，
∴AC＝1．
设BE＝a，则CE＝8﹣a，
根据翻折的性质可知，BE＝FE＝a，AF＝AB＝6，∠AFE＝∠B＝90°，
∴FC＝2．
在Rt△CEF中，EF＝a，CE＝8﹣a，CF＝2，
∴CE2＝EF2+CF2，即（8﹣a）2＝a2+22，
解得：a＝3，
∴8﹣a＝3．
故选：C．
本题考查了翻折变换、矩形的性质、勾股定理以及解一元二次方程，在Rt△CEF中，利用勾股定理找出关于a的一元二次方程是解题的关键．
4、B
【解析】
试题解析：∵四边形ABCD 是平行四边形，
∴BC=AD=12，AD∥BC，
∵四边形PDQB是平行四边形，
∴PD=BQ，
∵P的速度是1cm/秒，
∴两点运动的时间为12÷1=12s，
∴Q运动的路程为12×4=48cm，
∴在BC上运动的次数为48÷12=4次，
第一次PD=QB时，12-t=12-4t，解得t=0，不合题意，舍去；
第二次PD=QB时，Q从B到C的过程中，12-t=4t-12，解得t=4.8；
第三次PD=QB时，Q运动一个来回后从C到B，12-t=31-4t，解得t=8；
第四次PD=QB时，Q在BC上运动3次后从B到C，12-t=4t-31，解得t=9.1．
∴在运动以后，以P、D、Q、B四点组成平行四边形的次数有3次，
故选：B．
考点：平行四边形的判定与性质
5、C
【解析】
此题可以利用多边形的外角和和内角和定理求解．
【详解】
解：设所求多边形边数为n，由题意得
（n﹣2）•180°＝310°×2
解得n＝1．
则这个多边形是六边形．
故选C．
本题考查多边形的内角和与外角和、方程的思想．关键是记住内角和的公式与外角和的特征：任何多边形的外角和都等于310°，n边形的内角和为（n﹣2）•180°．
6、B
【解析】
方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
【详解】
解:∵s2丁＞s2丙＞s2甲＞s2乙，
方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．
∴乙最稳定．
故选：B．
本题考查了方差，正确理解方差的意义是解题的关键．
7、D
【解析】
过点D作DH⊥y轴，交y轴于H，根据矩形和正方形的性质可得∠EOF=∠BCF=∠HDE=90°，EF=BF=ED，BC=OA，根据角的和差故关系可得∠FBC=∠OFE=∠HED，∠BFC=∠OEF=∠HDE，利用ASA可证明△OFE≌△CBF≌△HDE，可得FC=OE=HD，BC=OF=HE，由点E为OA中点可得OF=2FC，即可求出FC的长，进而可得HE的长，即可求出OH的长，即可得点D坐标.
【详解】
过点D作DH⊥y轴，交y轴于H，
∵四边形是矩形，四边形是正方形，
∴∠EOF=∠BCF=∠HDE=∠EFB=90°，EF=BF=ED，BC=OA，
∴∠OFE+∠BFC=90°，∠FBC+∠BFC=90°，
∴∠OFE=∠FBC，
同理：∠OEF=∠BFC，
在△OEF和△CFB中，，
∴BC=OF=OA，FC=OE，
∵点E为OA中点，
∴OA=2OE，
∴OF=2OE，
∴OC=3OE，
∵点C坐标为（3，0），
∴OC=3，
∴OE=1，OF=2，
同理：△HDE≌△OEF，
∴HD=OE=1，HE=OF=2，
∴OH=OE+HE=3,
∴点D坐标为（1，3），
故选：D.
本题考查正方形的性质、矩形的性质及全等三角形的判定与性质，熟练掌握全等三角形的判定定理是解题关键.
8、B
【解析】
根据题目中的数据可以直接写出众数，求出相应的平均数和方差，从而可以解答本题．
【详解】
数据1，3，4，4，4，5，5，6的众数是4，
，
则s2＝=2，
故选B．
本题考查方差和众数，解答本题的关键是明确众数的定义，会求一组数据的方差．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、
【解析】
直接去括号，然后移项，即可得到答案.
【详解】
解：∵，
∴，
∴，
故答案为：.
本题考查了一元二次方程的一般式，解题的关键是熟练掌握一元二次方程的一般式.
10、①②④
【解析】
根据题意和条形统计图中的数据可以求得各个选项中对应的人数，从而可以解答本题．
【详解】
因为共有35人，而中位数应该是第18个数，所以第18个数是5，从图中看出第四个柱状图的范围在6以上，所以投4个球的有7人．可得：3球以下（含3球）的人数为10人，4球以下（含4球）的人数10+7=17人，6球以下（含6球）的人数35-1=1．故只有5球以下（含5球）的人数无法确定．
故答案为①②④
本题考查的是条形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．同时理解中位数的概念．
11、80°
【解析】
先由中位线定理推出，再由平行线的性质推出，然后根据直角三角形斜边上的中线等于斜边的一半得到HF=CF，最后由三角形内角和定理求出.
【详解】
∵点分别是的中点
∴（中位线的性质）
又∵
∴（两直线平行，内错角相等）
∵
∴（两直线平行，同位角相等）
又∵
∴三角形是三角形
∵是斜边上的中线
∴
∴（等边对等角）
∴
本题考查了中位线定理，平行线的性质，直角三角形斜边上的中线等于斜边的一半，和三角形内角和定理.熟记性质并准确识图是解题的关键．
12、3
【解析】
首先判断△BAE、△CAD是等腰三角形，从而得出BA=BE，CA=CD，由△ABC的周长为26，及BC=10，可得DE=6，利用中位线定理可求出PQ．
【详解】
由题知为的垂直平分线，
，由题意知为的垂直平分线，．
，且，．
．．
．又点，分别为，的中点，
．
本题考查等腰三角形的判定与性质，解题关键在于利用中位线定理求出PQ.
13、矩形是两条对角线相等的平行四边形．
【解析】
把命题的条件和结论互换就得到它的逆命题．
【详解】
命题”两条对角线相等的平行四边形是矩形“的逆命题是矩形是两条对角线相等的平行四边形，
故答案为矩形是两条对角线相等的平行四边形．
本题考查了互逆命题的知识，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题．
三、解答题（本大题共5个小题，共48分）
14、∠EFC=125°或145°.
【解析】
（1）首先作EP⊥CD于P，EQ⊥BC于Q，由∠DCA=∠BCA，得出EQ=EP,再由∠QEF+∠FEC=45°，得出∠PED+∠FEC=45°，进而得出∠QEF=∠PED，即可判定Rt△EQF≌Rt△EPD，得出EF=ED，即可得证；
（2）分类讨论：①当DE与AD的夹角为35°时，∠EFC=125°；②当DE与DC的夹角为35°时，∠EFC=145°，即可得解.
【详解】
（1）作EP⊥CD于P，EQ⊥BC于Q，如图所示
∵∠DCA=∠BCA
∴EQ=EP,
∵∠QEF+∠FEP=90°，∠PED+∠FEP=90°，
∴∠QEF=∠PED
在Rt△EQF和Rt△EPD中，
∴Rt△EQF≌Rt△EPD
∴EF=ED
∴矩形DEFG是正方形；
（2）①当DE与AD的夹角为35°时，
∠DEP=∠QEF=35°，
∴∠EFQ=90°-35°=55°，
∠EFC=180°-55°=125°；
②当DE与DC的夹角为35°时，
∠DEP=∠QEF=55°，
∴∠EFQ=90°-55°=35°，
∠EFC=180°-35°=145°；
综上所述，∠EFC=125°或145°.
此题主要考查正方形的性质、矩形的性质、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题.
15、（1）见解析；（2）见解析，AD=.
【解析】
（1）根据正方形的性质和AB的长度作图即可；
（2）利用数形结合的思想即可解决问题，由勾股定理可求出AD的长度.
【详解】
（1）如图，
（2）如图，
，
AD==．
本题考查作图-应用与设计、勾股定理、平行四边形的判定和性质等知识，解题的关键是学会利用数形结合的思想解决问题.
16、（1）50人，补图见解析；（2）10，13.1，12.5；（3）132人
【解析】
分析：
（1）由条形统计图中的信息可知，捐款15元的有14人，占被抽查人数的28%，由此可得被抽查学生的总人数为：14÷28%=50（人），由此可得捐款10元的人数为：50-9-14-7-4=16（人），这样即可补全条形统计图了；
（2）根据补充完整的条形统计图中的信息进行分析解答即可；
（3）由条形统计图中的信息计算出捐款在20元及以上的学生占捐款学生总数的比值，然后由600乘以所得比值即可得到所求结果.
详解：
（1）由条形统计图和扇形统计图中的信息可得：被抽查学生总数为：14÷28%=50（人），
∴捐款10元的人数为：50-9-14-7-4=16（人），
由此补全条形统计图如下图所示：
（2）由条形统计图中的信息可知：捐款金额的众数是：10元；
捐款金额的平均数为：（元）；
捐款金额的中位数为：（元）；
（3）根据题意可得：全校捐款20元及以上的人数有：（人）.
点睛：知道“条形统计图和扇形统计图中相关数据间的关系及众数、中位数和平均数的定义和确定方法”是解答本题的关键.
17、见解析,
【解析】
要证∠DAE=∠ECD．需先证△ADF≌△CEF，由折叠得BC=EC，∠B=∠AEC，由矩形得BC=AD，∠B=∠ADC=90°，再根据等量代换和对顶角相等可以证出，得出结论．
【详解】
证明：由折叠得：BC=EC，∠B=∠AEC，
∵矩形ABCD，
∴BC=AD，∠B=∠ADC=90°，
∴EC=DA，∠AEC=∠ADC=90°，
又∵∠AFD=∠CFE，
∴△ADF≌△CEF （AAS）
∴∠DAE=∠ECD．
本题考查折叠的性质、矩形的性质、全等三角形的性质和判定等知识，借助于三角形全等证明线段相等和角相等是常用的方法．
18、（1）见解析；（2）见解析；（3）（-1，0）．
【解析】
（1）利用网格特点和旋转的性质画出A、B、C的对应点A1、B1、C1即可；
（2）根据点A和A2的坐标特征确定平移的方向和距离，利用次平移规律写出点B2、C2的坐标，然后描点即可；、
（3）连接A1A2、C1C2、B1B2，它们都经过点（-1，0），从而得到旋转中心点P．
【详解】
解：（1）如图，△A1B1C1为所作；
（2）如图，△A2B2C2为所作．
（3）△A1B1C1绕点P旋转可得到△A2B2C2，则点P点坐标为（-1，0）．
故答案为：（1）见解析；（2）见解析；（3）（-1，0）．
本题考查作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了平移变换．
一、填空题（本大题共5个小题，每小题4分，共20分）
19、m＞﹣5且m≠0
【解析】
先解关于x的分式方程，求得x的值，然后再依据“解是正数”建立不等式求m的取值范围即可．
【详解】
去分母，得m=x-5，
即x=m+5，
∵方程的解是正数，
∴m+5＞0，即m＞-5，
又因为x-5≠0，
∴m≠0，
则m的取值范围是m＞﹣5且m≠0，
故答案为：m＞﹣5且m≠0.
本题考查了分式方程的解，熟练掌握分式方程的解法以及注意事项是解题的关键.这里要注意分母不等于0这个隐含条件.
20、70%
【解析】
利用合格的人数即50-10-5=35人，除以总人数即可求得．
【详解】
解：该班此次成绩达到合格的同学占全班人数的百分比是×100%=70%．
故答案是：70%．
本题考查了读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．
21、m＜3.
【解析】
试题分析：∵一次函数y=（2m-6）x+5中，y随x的增大而减小，
∴2m-6＜0，
解得，m＜3.
考点：一次函数图象与系数的关系．
22、
【解析】
将x的值代入x2-2x+2028=（x-1）2+2027，根据二次根式的运算法则计算可得．
【详解】
解：当x=1-时，
x2-2x+2028=（x-1）2+2027
=（1--1）2+2027
=（-）2+2027，
=3+2027
=1，
故答案为：1．
本题主要考查二次根式的化简求值，解题的关键是掌握二次根式的性质和运算法则及完全平方公式．
23、3
【解析】
连接DE，交AC于点P，连接BD．点B与点D关于AC对称，DE的长即为PE+PB的最小值,根据勾股定理即可得出DE的长度.
【详解】
连接DE，交AC于点P，连接BD．
∵点B与点D关于AC对称，
∴DE的长即为PE+PB的最小值，
∵AB=6，E是BC的中点，
∴CE=3，
在Rt△CDE中，
DE=
=
=
=3.
故答案为3．
主要考查轴对称，勾股定理等考点的理解，作出辅助线得出DE的长即为PE+PB的最小值为解决本题的关键.
二、解答题（本大题共3个小题，共30分）
24、（1） ；（2）；（3）．
【解析】
（1）由DE//BC，EF//DC，可证得四边形DCFE是平行四边形，求出DE=CF，DC=EF，由DC⊥BE，可得△BEF是直角三角形，利用勾股定理，求出BF的长即为BC+DE的值；
（2）同（1）做CE//DB，交AB延长线于点E，易证四边形DBEC是平行四边形，根据已知可证△DAB△CBA（SAS），得AC=DB，等量代换，可得AC=CE，故△ACE是等腰直角三角形，AE=8，利用勾股定理，即可求得AC；
（3）连接AE、CE，由四边形ABCD是平行四边形，四边形ABEF是矩形，易证得四边形DCEF是平行四边形，继而证得△ACE是等腰直角三角形，求出AC=CE，而DF=CE，即可得出答案．
【详解】
解：（1）∵DE//BC，EF//DC，
∴四边形DCFE是平行四边形，
∴DE=CF，DC=EF，
∴BC+ED=BC+CF=BF，
∵DC⊥BE，DC//EF，
∴∠BEF=90°，在Rt△BEF中，
∵BE=5，EF=DC=3，
∴BF==．
故BC+DE=．
（2）做CE//DB，交AB延长线于点E，
由（1）同理，可证得四边形DBEC是平行四边形，BE=DC=3，
在△DAB和△CBA中 ，
∴△DAB△CBA（SAS），
∴DB=AC，
∵四边形DBEC是平行四边形，DB=CE，
∴AC=CE，
∵AC⊥DB，
∴AC⊥CE，
∴△ACE是等腰直角三角形，
∵AE=AB+BE=AB+DC=5+3=8，
∴AC=，求得AC=．
故AC的长为．
（3）AC=DF；
证明：连接AE、CE，如图，
∵四边形ABCD是平行四边形，
∴AB//DC，
∵四边形ABEF是矩形，
∴AB//FE，BF=AE，
∴DC//FE，
∴四边形DCEF为平行四边形，
∴CE=DF，
∵四边形ABEF是矩形，
∴BF=AE，
∵BF=DF，
∴DF=CE，
∴AF=BE，
∵四边形ABCD是平行四边形，
∴AD=BC，
在△FAD和△EBC中 ，
∴△FAD△EBC（SSS），
∴∠AFD=∠BEC，
∴∠FEB=∠EFA=90°，
∵∠EBF=60°，∠BFD=30°，
∴∠DFA=90°-30°-（90°-60°）=30°，
∴∠CEB=30°，
∴OE=OB，
∵∠EBF=60°，
∴∠BEA=∠EBF=60°，
∴∠AEC=60°+30°=90°，
即△AEC是等腰直角三角形，
∴AC=CE，
∵DF=CE，
∴AC=DF．
故AC与DF之间的数量关系是AC=DF．
本题考查几何的综合，难度偏高，涉及的知识点有三角形、四边形、平行线等，熟练掌握以上知识点的综合运用是顺利解题的关键．
25、（1）每件衬衫应降价1元．（2）不可能，理由见解析
【解析】
（1）利用衬衣每件盈利×平均每天售出的件数=每天销售这种衬衣利润，列出方程解答即可．
（2）同样列出方程，若方程有实数根则可以，否则不可以．
【详解】
（1）设每件衬衫应降价x元．
根据题意，得 （40-x）（1+2x）=110
整理，得x2-30x+10=0
解得x1=10，x2=1．
∵“扩大销售量，减少库存”，
∴x1=10应略去，
∴x=1．
答：每件衬衫应降价1元．
（2）不可能．理由如下：
令y=（40-x）（1+2x），
当y=1600时，（40-x）（1+2x）=1600
整理得x2-30x+400=0
∵△=900-4×400＜0，
方程无实数根．
∴商场平均每天不可能盈利1600元．
此题主要考查了一元二次方程的应用和根的判别式，利用基本数量关系：平均每天售出的件数×每件盈利=每天销售的利润是解题关键．
26、（1）AC=，QD=；（2）是菱形，理由见解析；（3）DP2+ EF2=4QD2，理由见解析；（4）垂直且相等，理由见解析.
【解析】
（1）利用勾股定理求出AC，再证明△FDQ≌△FPA得到QD=AP，结合CD=CP求出结果；
（2）先证明DE∥PF，结合EP∥DF得到四边形DFPE是平行四边形，再由EF⊥DP得到菱形；
（3）根据菱形的性质得到2DG=DP，2GF=EF，再证明QD=DF，最后利用勾股定理证明线段关系；
（4）证明△ADE≌BAP，得到AE=BP，∠EAD=∠ABP，延长BP，与AE交于点H，利用∠EAD=∠ABP，得到∠PHA=90°，即可判定关系.
【详解】
解：（1）AC=，
∵CF平分∠BCD，FD⊥CD，FP⊥AC，
∴FD=FP，又∠FDQ=∠FPA，∠DFQ=∠PFA，
∴△FDQ≌△FPA（ASA），
∴QD=AP，
∵点P在正方形ABCD对角线AC上，
∴CD=CP=a，
∴QD=AP=AC-PC=；
（2）∵FD=FP，CD=CP，
∴CF垂直平分DP，即DP⊥CF，
∴ED=EP，则∠EDP=∠EPD，
∵FD=FP，
∴∠FDP=∠FPD，
而EP∥DF，
∴∠EPD=∠FDP，
∴∠FPD=∠EPD，
∴∠EDP=∠FPD，
∴DE∥PF，而EP∥DF，
∴四边形DFPE是平行四边形，
∵EF⊥DP，
∴四边形DFPE是菱形；
（3）DP2+ EF2=4QD2，理由是：
∵四边形DFPE是菱形，设DP与EF交于点G，
∴2DG=DP，2GF=EF，
∵∠ACD=45°，FP⊥AC，
∴△PCQ为等腰直角三角形，
∴∠Q=45°，
可得△QDF为等腰直角三角形，
∴QD=DF，
在△DGF中，DG2+FG2=DF2，
∴有（DP）2+（EF）2=QD2，
整理得：DP2+ EF2=4QD2；
（4）∵∠DFQ=45°，DE∥FP，
∴∠EDF=45°，
又∵DE=DF=DQ=AP=，AD=AB，
∴△ADE≌BAP（SAS），
∴AE=BP，∠EAD=∠ABP，
延长BP，与AE交于点H，
∵∠HPA=∠PAB+∠PBA=∠PAB+∠DAE，
∠PAB+∠DAE+∠HAP=90°，
∴∠HPA+∠HAP=90°，
∴∠PHA=90°，即BP⊥AE，
综上：BP与AE的关系是：垂直且相等.
本题考查了正方形的性质，等腰直角三角形的判定和性质，全等三角形的判定和性质，菱形的判定，勾股定理，知识点较多，解题时应当注意各个小问之间的关系，找到能够利用的结论和条件.
题号
一
二
三
四
五
总分
得分
批阅人
选手
甲
乙
丙
丁
方差（s2）
0.020
0.019
0.021
0.022