

2024-2025学年江苏省镇江外国语学校九年级(上)第一次月考数学试卷(含答案)
展开一、选择题:本题共9小题,每小题3分,共27分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知Rt△ABC中,∠C=90°,AC=3,BC=4,以C为圆心,r为半径的圆与边AB有两个交点,则r的取值范围是( )
A. r=125B. r>125C. 3
A. −1B. 0C. 1D. −1或1
3.一个等腰三角形的两条边长分别是方程2x2−13x+15=0的两根,则该等腰三角形的周长是( )
A. 8B. 11.5C. 10D. 8或11.5
4.已知a是方程x2+x−1=0的一个根,则2a2−1−1a2−a的值为( )
A. −1+ 52B. −1± 52C. −1D. 1
5.关于x的方程a(x+m)2+b=0的解是x1=−2,x2=1(a,m,b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是( )
A. x1=−2,x2=1B. x1=1,x2=3
C. x1=−4,x2=−1D. 无法求解
6.已知关于x的一元二次方程x2−x+14m=0有实数根,设此方程得一个实数根为t,令y=4t2−4t−5m+4,则( )
A. y>−2B. y≥−2C. y≤−2D. y<−2
7.已知关于x的方程ax2+bx+c=5的一个根是2,且二次函数y=ax2+bx+c的对称轴是直线x=2,则这条抛物线的顶点坐标为( )
A. (2,−3)B. (2,1)C. (2,5)D. (5,2)
8.如图,在同一平面直角坐标系中,函数y=ax+2(a≠0)与y=−ax2−2x(a≠0)的图象可能是( )
A. B. C. D.
9.若抛物线y=x2+ax+b与x轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线x=1,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )
A. (−3,−6)B. (−3,0)C. (−3,−5)D. (−3,−1)
二、填空题:本题共11小题,每小题3分,共33分。
10.已知关于x的方程(m+2)x2+4mx+1=0是一元二次方程,则m的取值范围是______.
11.方程x2−2021x=0中较小的根是______.
12.如图,在平面直角坐标系中,点A、B的坐标分别为(0,1)和( 3,0),则△OAB外接圆的圆心坐标是______.
13.若一个三角形两条边长为和2和4,第三边长满足方程x2−7x+10=0,则此三角形的周长为______.
14.关于x的一元二次方程kx2+2x−1=0有两个不相等的实数根,则k的取值范围是______.
15.如图,在等腰直角△ABC中,斜边AB的长度为8,以AC为直径作圆,点P为半圆上
的动点,连接BP,取BP的中点M,则CM的最小值为______.
16.若一元二次方程x2−x+a=0有实数根,则a的取值范围是______.
17.已知a−b=8,ab+16≤0,则a+2b的值为______.
18.如图,在△AOB中,∠AOB=90°,∠A=30°,OB=4,以O为圆心,OB为半径画弧,分别交OA、AB于点C、D,则阴影部分面积为______(结果保留π).
19.已知抛物线y=ax2+bx+c的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线过原点;②4a+b=0;③a−b+c<0;④b2>4ac;⑤当x<2时,y随x的增大而增大,你认为其中正确的是______.(填序号)
20.当x≤1时,二次函数y=−(x−m)2+m2+1有最大值4,则实数m的值为______.
三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
21.(本小题8分)
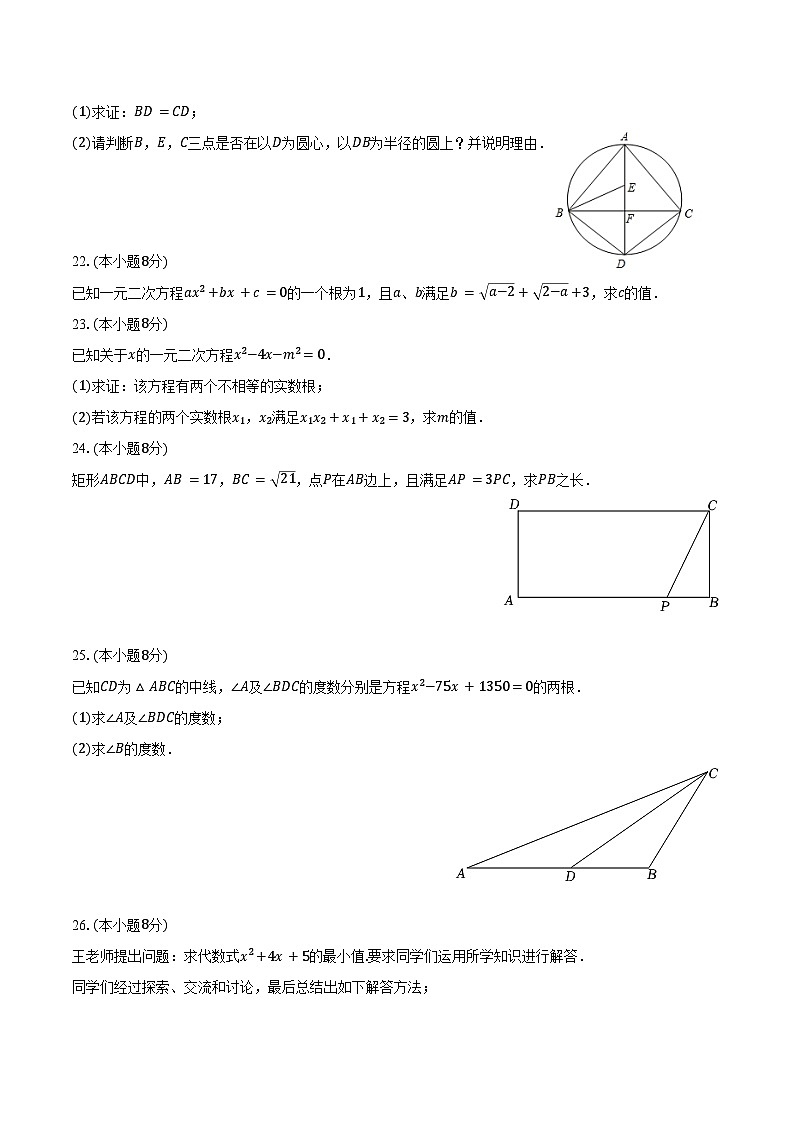
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
22.(本小题8分)
已知一元二次方程ax2+bx+c=0的一个根为1,且a、b满足b= a−2+ 2−a+3,求c的值.
23.(本小题8分)
已知关于x的一元二次方程x2−4x−m2=0.
(1)求证:该方程有两个不相等的实数根;
(2)若该方程的两个实数根x1,x2满足x1x2+x1+x2=3,求m的值.
24.(本小题8分)
矩形ABCD中,AB=17,BC= 21,点P在AB边上,且满足AP=3PC,求PB之长.
25.(本小题8分)
已知CD为△ABC的中线,∠A及∠BDC的度数分别是方程x2−75x+1350=0的两根.
(1)求∠A及∠BDC的度数;
(2)求∠B的度数.
26.(本小题8分)
王老师提出问题:求代数式x2+4x+5的最小值.要求同学们运用所学知识进行解答.
同学们经过探索、交流和讨论,最后总结出如下解答方法;
解:x2+4x+5=x2+4x+22−22+5=(x+2)2+1,
∵(x+2)2≥0,∴(x+2)2+1≥1.
当(x+2)2=0时,(x+2)2+1的值最小,最小值是1.
∴x2+4x+5的最小值是1.
请你根据上述方法,解答下列各题:
(1)直接写出(x−1)2+3的最小值为______.
(2)求代数式x2+10x+32的最小值.
(3)你认为代数式−13x2+2x+5有最大值还是有最小值?求出该最大值或最小值.
(4)若7x−x2+y−11=0,求x+y的最小值.
27.(本小题8分)
如图一,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.
(1)求证:∠CAD=∠BAC;
(2)如图二,若把直线EF向上移动,使得EF与⊙O相交于G,C两点(点C在点G的右侧),连接AC,AG,若题中其他条件不变,这时图中是否存在与∠CAD相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.
参考答案
1.D
2.A
3.B
4.D
5.C
6.B
7.C
8.D
9.B
10.m≠−2
11.0
12.( 32,12)
13.11
14.k>−1且k≠0
15. 10− 2
16.a≤14
17.−4
18.4 3−4π3
19.①②④
20.2或− 3
21.(1)证明:∵AD为直径,AD⊥BC,
∴由垂径定理得:BD=CD
∴根据圆心角、弧、弦之间的关系得:BD=CD.
(2)解:B,E,C三点在以D为圆心,以DB为半径的圆上.
理由:由(1)知:BD=CD,
∴∠1=∠2,
又∵∠2=∠3,
∴∠1=∠3,
∴∠DBE=∠3+∠4,∠DEB=∠1+∠5,
∵BE是∠ABC的平分线,
∴∠4=∠5,
∴∠DBE=∠DEB,
∴DB=DE.
由(1)知:BD=CD
∴DB=DE=DC.
∴B,E,C三点在以D为圆心,以DB为半径的圆上.(7分)
22.解:∵a−2≥0,a−2≤0,
∴a=2,
∴b=3,
∵一元二次方程ax2+bx+c=0的一个根是1,
∴a+b+c=0,
∴2+3+c=0,
∴c=−5.
23.(1)证明:△=b2−4ac=(−4)2−4×(−m2)=16+4m2.
∵m2≥0,
∴16+4m2>0,即△>0,
∴该方程有两个不相等的实数根.
(2)解:∵方程x2−4x−m2=0的两个实数根分别为x1、x2,
∴x1+x2=4,x1x2=−m2.
又∵x1x2+x1+x2=3,
∴−m2+4=3,即m2=1,
解得m=±1.
故m的值为±1.
24.解:设PB为x,则AP=17−x,
∵AP=3PC,
∴PC=17−x3,
在Rt△PBC中,PC2=PB2+BC2,
∴x2+21=(17−x3)2,
∴4x2−17x−50=0,
解得:x1=2,x2=−254(不符合题意舍去),
答:PB之长为2.
25.解:(1)x2−75x+1350=0,
(x−30)(x−45)=0,
x−30=0或x−45=0,
x1=30,x2=45,
∵∠BDC=∠A+∠ACD,
∴∠BDC>∠A,
∴∠BDC=45°,∠A=30°
∴∠A的度数为30°,∠BDC的度数为45°;
(2)过点B作BH⊥AC,垂足为H,连接HD,
∴∠AHB=∠CHB=90°,
∵∠A=30°,
∴∠ABH=90°−∠A=60°,
∵DH是斜边AB上的中线,
∴DH=BD=12AB,
∴△BHD是等边三角形,
∴HD=HB,∠HDB=∠ABH=60°,
∵∠BDC=45°,
∴∠HDC=∠HDB−∠BDC=15°,
∵∠ACD=∠BDC−∠A=15°,
∴∠ACD=∠HDC=15°,
∴HD=HC,
∴HB=HC,
∴∠HBC=∠HCB=45°,
∴∠ABC=∠ABH+∠HBC=105°,
∴∠ABC的度数为105°.
26.(1)3;
(2)x2+10x+32=x2+10x+25−25+32=(x+5)2+7,
∵(x+5)2≥0,∴(x+5)2+7≥7.
当(x+5)2=0时,(x+5)2+7的值最小,最小值是7,
∴x2+10x+32的最小值是7;
(3)−13x2+2x+5
=−13(x2−6x)+5
=−13(x2−6x+9−9)+5
=−13(x−3)2+3+5
=−13(x−3)2+8,
∵(x−3)2≥0,
∴−13(x−3)2≤0,
∴−13(x−3)2+8≤8,
∴当(x−3)2=0时,−13x2+2x+5有最大值,最大值是8;
(4)∵7x−x2+y−11=0,
∴y=x2−7x+11
∴x+y
=x+x2−7x+11
=x2−6x+11
=x2−6x+9+2
=(x−3)2+2,
∵(x−3)2≥0,
∴(x−3)2+2≥2,
当(x−3)2=0时,(x−3)2+2的值最小,最小值是2.
∴x+y的最小值是2.
27.(1)证明:如图一,连接OC,则OC⊥EF,且OC=OA,
易得∠OCA=∠OAC.
∵AD⊥EF,
∴OC//AD.
∴∠OCA=∠CAD,
∴∠CAD=∠OAC.
即∠CAD=∠BAC.
(2)解:与∠CAD相等的角是∠BAG.
证明如下:
如图二,连接BG.
∵四边形ACGB是⊙O的内接四边形,
∴∠ABG+∠ACG=180°.
∵D,C,G共线,
∴∠ACD+∠ACG=180°.
∴∠ACD=∠ABG.
∵AB是⊙O的直径,
∴∠BAG+∠ABG=90°
∵AD⊥EF
∴∠CAD+∠ACD=90°
∴∠CAD=∠BAG.
2024-2025学年江苏省镇江外国语学校九年级(上)第一次月考数学试卷(含解析): 这是一份2024-2025学年江苏省镇江外国语学校九年级(上)第一次月考数学试卷(含解析),共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2024-2025学年江苏省镇江外国语学校八年级(上)第一次月考数学试卷(含解析): 这是一份2024-2025学年江苏省镇江外国语学校八年级(上)第一次月考数学试卷(含解析),共24页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
江苏省镇江市外国语学校2024-2025学年九年级上学期第一次月考数学试题(解析版): 这是一份江苏省镇江市外国语学校2024-2025学年九年级上学期第一次月考数学试题(解析版),共21页。












