2024年江西省抚州市南城县数学九上开学质量检测模拟试题【含答案】

这是一份2024年江西省抚州市南城县数学九上开学质量检测模拟试题【含答案】，共20页。试卷主要包含了选择题，填空题，解答题，六月份平均增长率为.等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
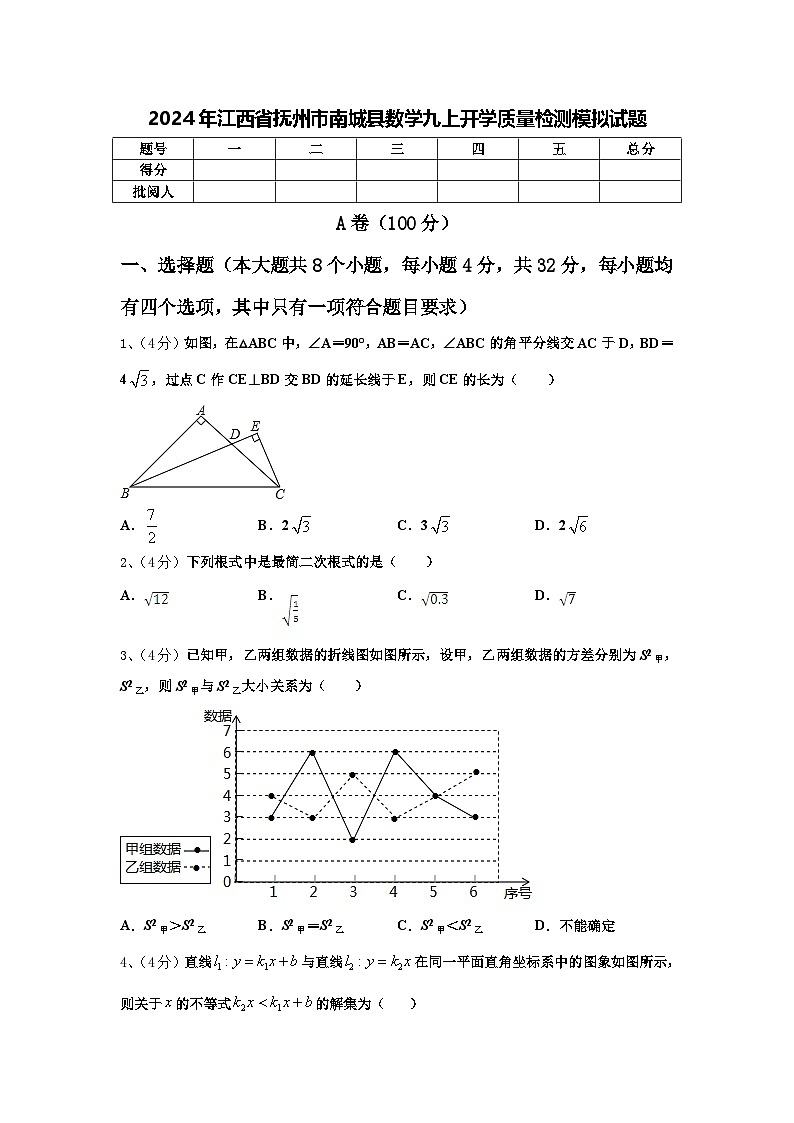
1、（4分）如图，在△ABC中，∠A＝90°，AB＝AC，∠ABC的角平分线交AC于D，BD＝4，过点C作CE⊥BD交BD的延长线于E，则CE的长为（ ）
A．B．2C．3D．2
2、（4分）下列根式中是最简二次根式的是（ ）
A．B．C．D．
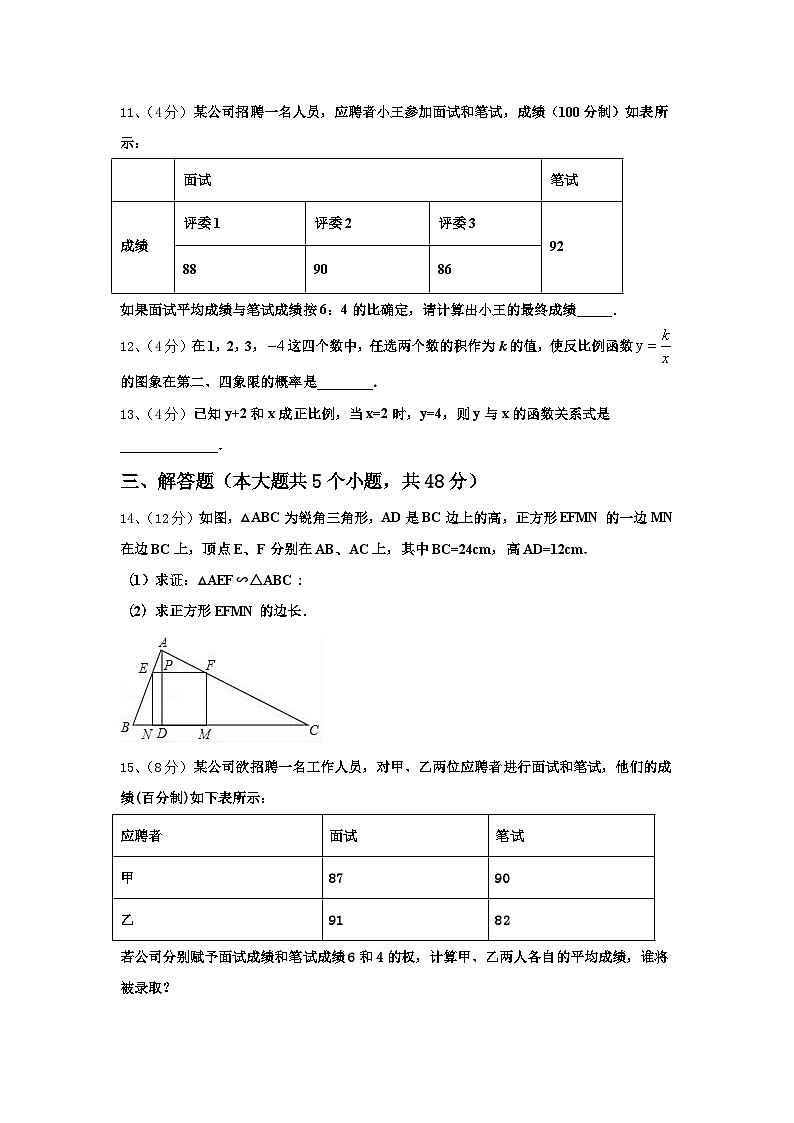
3、（4分）已知甲，乙两组数据的折线图如图所示，设甲，乙两组数据的方差分别为S2甲，S2乙，则S2甲与S2乙大小关系为（ ）
A．S2甲＞S2乙B．S2甲＝S2乙C．S2甲＜S2乙D．不能确定
4、（4分）直线与直线在同一平面直角坐标系中的图象如图所示，则关于的不等式的解集为（ ）
A．B．C．D．
5、（4分）下列命题的逆命题正确的是（ ）
A．如果两个角都是45°，那么它们相等B．全等三角形的周长相等
C．同位角相等，两直线平行D．若a=b，则
6、（4分）函数y=kx﹣3与y=（k≠0）在同一坐标系内的图象可能是（ ）
A．B．C．D．
7、（4分）若点A（3－m，n+2）关于原点的对称点B的坐标是（－3，2），则m，n的值为（ ）
A．m=－6，n=－4B．m=O，n=－4
C．m=6，n=4D．m=6，n=－4
8、（4分）下列计算过程中，结果是2的是
A．B．C．D．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）已知函数是关于的一次函数，则的值为_____．
10、（4分）长、宽分别为a、b的矩形，它的周长为14，面积为10，则a2b+ab2的值为_____．
11、（4分）某公司招聘一名人员，应聘者小王参加面试和笔试，成绩（100分制）如表所示：
如果面试平均成绩与笔试成绩按6：4的比确定，请计算出小王的最终成绩_____．
12、（4分）在1，2，3，这四个数中，任选两个数的积作为k的值，使反比例函数的图象在第二、四象限的概率是________.
13、（4分）已知y+2和x成正比例，当x=2时，y=4，则y与x的函数关系式是______________．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，△ABC为锐角三角形，AD是BC边上的高，正方形EFMN的一边MN在边BC上，顶点E、F分别在AB、AC上，其中BC=24cm，高AD=12cm．
（1）求证：△AEF∽△ABC：
（2）求正方形EFMN的边长．
15、（8分）某公司欲招聘一名工作人员，对甲、乙两位应聘者进行面试和笔试，他们的成绩(百分制)如下表所示：
若公司分别赋予面试成绩和笔试成绩6和4的权，计算甲、乙两人各自的平均成绩，谁将被录取？
16、（8分）如图，点D是△ABC内一点，点E，F，G，H分别是AB，AC，CD，BD的中点。
（1）求证：四边形EFGH是平行四边形；（2）已知AD＝6，BD＝4，CD＝3，∠BDC＝90°，求四边形EFGH的周长。
17、（10分）某农机厂四月份生产某型号农机台，第二季度（包括四、五、六三个月）共生产该型号农机台.求该农机厂五、六月份平均增长率.
18、（10分）一个二次函数的图象经过三点.求这个二次函数的解析式并写出图象的开口方向、对称轴和顶点.
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）写一个无理数，使它与的积是有理数：________。
20、（4分）使分式的值为整数的所有整数的和是________．
21、（4分）甲乙两人在5次打靶测试中，甲成绩的平均数，方差，乙成绩的平均数，方差.教练根据甲、乙两人5次的成绩，选一名队员参加射击比赛，应选择__________.
22、（4分）将一次函数y＝﹣2x﹣1的图象向上平移3个单位，则平移后所得图象的解析式是_____．
23、（4分）我市某一周每天的最低气温统计如下（单位：℃）：﹣1，﹣4，6，0，﹣1，1，﹣1，则这组数据的众数为__________．
二、解答题（本大题共3个小题，共30分）
24、（8分）已知：如图，在□ABCD中，点E在AB上，点F在CD上，且DE∥BF．求证：DE = BF．
25、（10分）如图1，正方形ABCD中，E为BC上一点，过B作BG⊥AE于G，延长BG至点F使∠CFB=45°
（1）求证：AG=FG；
（2）如图2延长FC、AE交于点M，连接DF、BM，若C为FM中点，BM=10，求FD的长．
26、（12分）如图，已知AD∥BC，AB⊥BC，AB＝BC＝4，P为线段AB上一动点．将△BPC沿PC翻折至△EPC，延长CE交射线AD于点D

（1）如图1，当P为AB的中点时，求出AD的长
（2）如图2，延长PE交AD于点F，连接CF，求证：∠PCF＝45°
（3）如图3，∠MON＝45°，在∠MON内部有一点Q，且OQ＝8，过点Q作OQ的垂线GH分别交OM、ON于G、H两点．设QG＝x，QH＝y，直接写出y关于x的函数解析式
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
延长CE与BA延长线交于点F，首先证明△BAD≌△CAF，根据全等三角形的性质可得BD＝CF，再证明△BEF≌△BCE可得CE＝EF，进而可得CE＝BD，即可得出结果．
【详解】
证明：延长CE与BA延长线交于点F，
∵∠BAC＝90°，CE⊥BD，
∴∠BAC＝∠DEC，
∵∠ADB＝∠CDE，
∴∠ABD＝∠DCE，
在△BAD和△CAF中，
，
∴△BAD≌△CAF（ASA），
∴BD＝CF，
∵BD平分∠ABC，CE⊥DB，
∴∠FBE＝∠CBE，
在△BEF和△BCE中，
，
∴△BEF≌△BCE（AAS），
∴CE＝EF，
∴DB＝2CE，即CE＝BD＝×4＝2，
故选：B．
本题考查了全等三角形的判定与性质、角平分线定义，熟练掌握全等三角形的判定方法，全等三角形对应边相等是解题的关
2、D
【解析】
判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．
【详解】
A、，不是最简二次根式，本项错误；
B、，不是最简二次根式，本项错误；
C、，不是最简二次根式，本项错误；
D、是最简二次根式，本项正确；
故选择：D.
本题考查最简二次根式的定义．最简二次根式必须满足两个条件：
（1）被开方数不含分母；
（2）被开方数不含能开得尽方的因数或因式．
3、A
【解析】
通过折线统计图中得出甲、乙两个组的各个数据，进而求出甲、乙的平均数，甲、乙的方差，进而做比较得出答案．
【详解】
甲的平均数：（3+6+2+6+4+3）÷6＝4，乙的平均数：（4+3+5+3+4+5）÷6＝4，
＝[（3﹣4）2+（6﹣4）2+（2﹣4）2+（6﹣4）2+（4﹣4）2+（3﹣4）2]≈2.33，
＝[（4﹣4）2+（3﹣4）2+（5﹣4）2+（3﹣4）2+（4﹣4）2+（5﹣4）2]≈1.33，
∵2.33＞1.33
∴＞，
故选：A．
本题主要考查方差的意义，掌握方差的计算公式，是解题的关键．
4、C
【解析】
由图象可以知道，当x=-1时，两个函数的函数值是相等的，再根据函数的增减性可以判断出不等式k2x＜k1x+b解集．
【详解】
两条直线的交点坐标为（-1，2），且当x＞-1时，直线l2在直线l1的下方，故不等式k2x＜k1x+b的解集为x＞-1．
故选：C．
此题考查一次函数的图象，解一元一次不等式，解题关键在于掌握两个图象的“交点”是两个函数值大小关系的“分界点”，在“分界点”处函数值的大小发生了改变．
5、C
【解析】
交换原命题的题设与结论得到四个命题的逆命题，然后分别根据三角形的概念、全等三角形的判定、平行线的性质和平方根的定义判定四个逆命题的真假．
【详解】
A. 逆命题为：如果两个角相等，那么它们都是45°，此逆命题为假命题；
B. 逆命题为：周长相等的两三角形全等，此逆命题为假命题；
C. 逆命题为：两直线平行，同位角相等，此逆命题为真命题；
D. 逆命题为：若a2=b2，则a=b，此逆命题为假命题.
故选C.
本题考查命题与定理，解题的关键是掌握三角形的概念、全等三角形的判定、平行线的性质和平方根的定义.
6、B
【解析】
分析：根据当k＞0、当k＜0时，y=kx-3和y=（k≠0）经过的象限，二者一致的即为正确答案．
详解：∵当k＞0时，y=kx-3过一、三、四象限，反比例函数y=过一、三象限，
当k＜0时，y=kx-3过二、三、四象限，反比例函数y=过二、四象限，
∴B正确；
故选B．
点睛：本题主要考查了反比例函数的图象性质和一次函数的图象性质，关键是由k的取值确定函数所在的象限．
7、B
【解析】
试题分析：关于原点对称的两点的横纵坐标分别互为相反数，则3－m=3，n+2=－2，解得：m=0，n=－4.
考点：原点对称
8、C
【解析】
根据负指数幂运算法则、0次幂的运算法则、相反数的意义、绝对值的性质逐项进行判断即可得．
【详解】
解：A、原式，故不符合题意；
B、原式，故不符合题意；
C、原式=2，故符合题意；
D、原式，故不符合题意，
故选C．
本题考查了负指数幂、0次幂、相反数、绝对值等，熟练掌握各运算的运算法则以及相关的性质是解题的关键．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、－1
【解析】
根据一次函数的定义，可得答案.
【详解】
解：由是关于x的一次函数，得
，解得m=-1.
本题主要考查了一次函数的定义，一次函数y=kx+b的定义条件是：k、b为常数，k≠0，自变量次数为1.
10、1．
【解析】
由周长和面积可分别求得a+b和ab的值，再利用因式分解把所求代数式可化为ab（a+b），代入可求得答案
【详解】
∵长、宽分别为a、b的矩形，它的周长为14，面积为10，
∴a+b==7，ab=10，
∴a2b+ab2=ab（a+b）=10×7=1，
故答案为：1．
本题主要考查因式分解的应用，把所求代数式化为ab（a+b）是解题的关键．
11、89.6分
【解析】
将面试所有的成绩加起来再除以3即可得小王面试平均成绩，再根据加权平均数的含义和求法，求出小王的最终成绩即可．
【详解】
∵面试的平均成绩为=88（分），
∴小王的最终成绩为=89.6（分），
故答案为89.6分．
此题主要考查了加权平均数的含义和求法，要熟练掌握，解答此题的关键是要明确：数据的权能够反映数据的相对“重要程度”，要突出某个数据，只需要给它较大的“权”，权的差异对结果会产生直接的影响．同时考查了算术平均数的含义和求法，要熟练掌握，解答此题的关键是要明确：算术平均数是加权平均数的一种特殊情况，加权平均数包含算术平均数，当加权平均数中的权相等时，就是算术平均数．
12、
【解析】
四个数任取两个有6种可能．要使图象在第四象限，则k