2024年聊城市重点中学数学九年级第一学期开学统考试题【含答案】

这是一份2024年聊城市重点中学数学九年级第一学期开学统考试题【含答案】，共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）如图．在菱形ABCD中，对角线AC，BD交于点O，下列说法错误的是（ ）
A．AB∥DC B．AC=BD C．AC⊥BD D．OA=OC
2、（4分）已知点P在第四象限，且到x轴的距离为3，到y轴的距离为2，则点P的坐标为（ ）
A．（－2，3）B．（2，－3）C．（3，－2）D．（－3，2）
3、（4分）甲、乙、丙、丁四位同学在一次数学测验中的平均成绩是90分，而甲、乙、丙三人的平均成绩是88分，下列说法一定正确的是（ ）
A．丁同学的成绩比其他三个同学的成绩都好
B．四位同学成绩的中位数一定是其中一位同学的成绩
C．四位同学成绩的众数一定是90分
D．丁同学成绩是96分
4、（4分）若，则的值为（ ）
A．B．C．D．
5、（4分）平南县某小区5月份随机抽取了15户家庭，对其用电情况进行了统计，统计情况如下（单位：度）：78，62，95，108，87，103，99，74，87，105，88，76，76，94，79.则用电量在71~80的家庭有（ ）
A．4户B．5户C．6户D．7户
6、（4分）下列计算中，运算错误的是（ ）
A．B．
C．D．(-)2=3
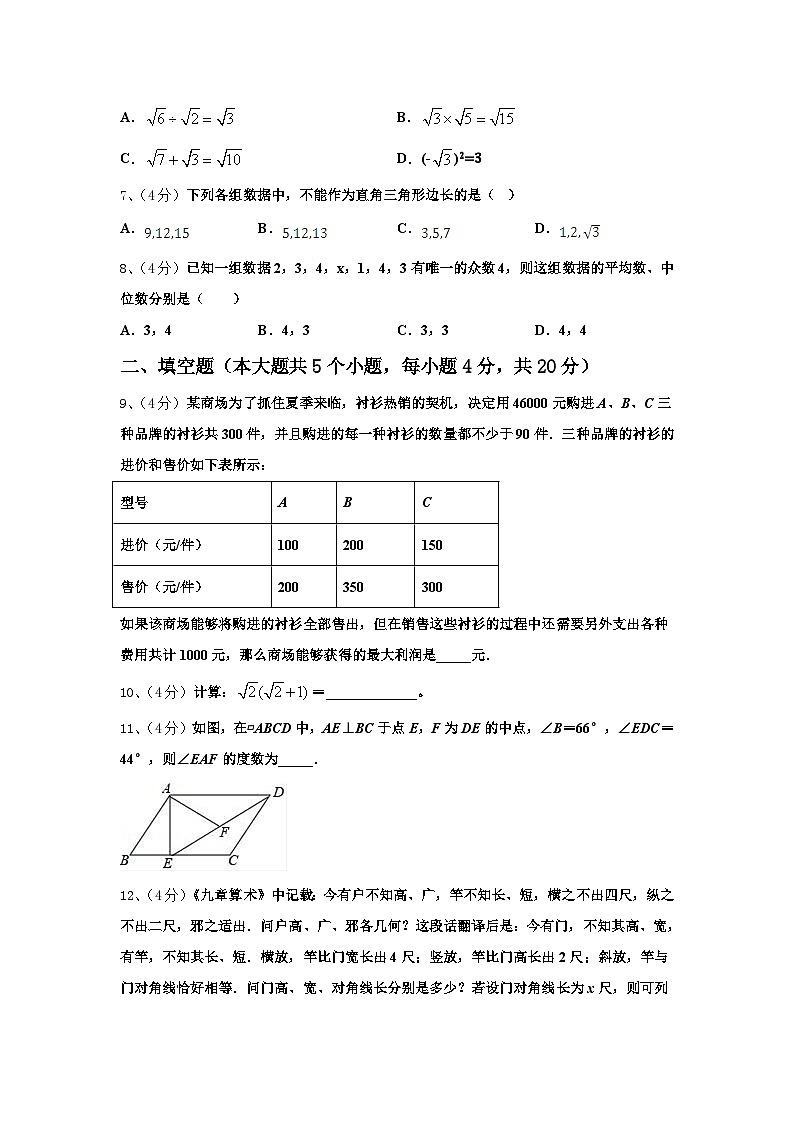
7、（4分）下列各组数据中，不能作为直角三角形边长的是（ ）
A．B．C．D．
8、（4分）已知一组数据2，3，4，x，1，4，3有唯一的众数4，则这组数据的平均数、中位数分别是（ ）
A．3，4B．4，3C．3，3D．4，4
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）某商场为了抓住夏季来临，衬衫热销的契机，决定用46000元购进A、B、C三种品牌的衬衫共300件，并且购进的每一种衬衫的数量都不少于90件．三种品牌的衬衫的进价和售价如下表所示：
如果该商场能够将购进的衬衫全部售出，但在销售这些衬衫的过程中还需要另外支出各种费用共计1000元，那么商场能够获得的最大利润是_____元．
10、（4分）计算：＝_____________。
11、（4分）如图，在▱ABCD中，AE⊥BC于点E，F为DE的中点，∠B＝66°，∠EDC＝44°，则∠EAF的度数为_____．
12、（4分）《九章算术》中记载：今有户不知高、广，竿不知长、短，横之不出四尺，纵之不出二尺，邪之适出．问户高、广、邪各几何？这段话翻译后是：今有门，不知其高、宽，有竿，不知其长、短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线恰好相等．问门高、宽、对角线长分别是多少？若设门对角线长为x尺，则可列方程为_____．
13、（4分）写出一个经过二、四象限的正比例函数_________________________．
三、解答题（本大题共5个小题，共48分）
14、（12分）如图，在四边形ABCD中，AD//BC，∠A=∠C，CD=2AD，BE⊥AD于点E，F为CD的中点，连接EF、BF．
（1）求证：四边形ABCD是平行四边形；
（2）求证：BF平分∠ABC；
（3）请判断△BEF的形状，并证明你的结论.
15、（8分）如图，一次函数y=k2x+b的图象与y轴交于点B，与正比例函数y=k1x的图象相交于点A（4，3），且OA=OB．
（1）分别求出这两个函数的解析式；
（2）求△AOB的面积；
16、（8分）如图，在的方格中，的顶点均在格点上．试按要求画出线段（，均为格点），各画出一条即可．

17、（10分）已知：AC是菱形ABCD的对角线，且AC=BC．
(1)如图①，点P是△ABC的一个动点，将△ABP绕着点B旋转得到△CBE．
①求证：△PBE是等边三角形；
②若BC=5，CE=4，PC=3，求∠PCE的度数；
(2)连结BD交AC于点O，点E在OD上且DE=3，AD=4，点G是△ADE内的一个动点如图②，连结AG，EG，DG，求AG+EG+DG的最小值．
18、（10分）（1）计算： （2）计算：
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）某公司招聘一名公关人员甲，对甲进行了笔试和面试，其面试和笔试的成绩分别为86分和90分，面试成绩和笔试成绩的权分别是6和4，则甲的平均成绩为__分．
20、（4分）数据101，98，102，100，99的方差是______．
21、（4分）关于x的一元二次方程(2m-6)x2+x-m2+9=0的常数项为0，则实数m=_______
22、（4分）如图是一种贝壳的俯视图，点C分线段AB近似于黄金分割（AC>BC）．已知AB=10cm，则AC的长约为__________cm．（结果精确到0.1cm）
23、（4分）如图，△ABC中，D，E分别为AB，AC的中点，∠B=70°，则∠ADE= 度．
二、解答题（本大题共3个小题，共30分）
24、（8分） “端午节”某顾客到商场购买商品，发现如果购买3件A商品和2件B商品共需花费230元，如果购买4件A商品和1件B商品共需花费240元．
（1）求A商品、B商品的单价分别是多少元？
（2）商场在“端午节”开展促销活动，促销方法是：购买A商品超过10件，超过部分可以享受6折优惠，若购买x（x＞0）件A商品需要花费y元，请你求出y与x的函数关系式．
（3）在（2）的条件下，顾客决定在A、B两种商品中选购其中一种，且数量超过10件，请你帮助顾客判断买哪种商品省钱．
25、（10分）如果P 是正方形ABCD 内的一点，且满足∠APB＋∠DPC＝180°，那么称点P 是正方形 ABCD 的“对补点”.
（1）如图1，正方形ABCD 的对角线AC，BD 交于点M，求证：点M 是正方形ABCD 的对补点；
（2）如图2，在平面直角坐标系中，正方形ABCD 的顶点A（1，1），C（3，3）.除对角线交点外，请再写出一个该正方形的对补点的坐标，并证明.
26、（12分）如图，在△ABD中，AB=AD，将△ABD沿BD对折，使点A翻折到点C，E是BD上一点。且BE>DE，连接AE并延长交CD于F，连接CE.
(1)依题意补全图形；
(2)判断∠AFD与∠BCE的大小关系并加以证明；
(3)若∠BAD=120°，过点A作∠FAG=60°交边BC于点G，若BG=m，DF=n，求AB的长度(用含m，n的代数式表示).
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、B
【解析】
A．菱形的对边平行且相等，所以AB∥DC，故本选项正确；
B．菱形的对角线不一定相等；
C．菱形的对角线互相垂直，所以AC⊥BD，故本选项正确；
D．菱形的对角线互相平分，所以OA＝OC，故本选项正确．故选B．
2、B
【解析】
试题分析：根据点P在第四象限，所以P点的横坐标在x轴的正半轴上，纵坐标在y轴的负半轴上，由P点到x轴的距离为3，到y轴的距离为2，即可推出P点的横、纵坐标，从而得出（2，-3）．
故选B．
考点：平面直角坐标系
3、D
【解析】
根据算术平均数的定义，中位数的定义以及众数的定义对各选项分析判断利用排除法求解．
【详解】
.解：A、丁同学的成绩为90×4﹣88×3＝96（分），而由甲、乙、丙三人的平均成绩是88分无法判断三人的具体成绩，无法比较，此选项错误；
B、四位同学成绩的中位数可能是四个数据中的一个，也可能不在所列数据中，此选项错误；
C、由于不清楚四位同学的各自成绩，所以不能判断众数，此选项错误；
D、丁同学的成绩为90×4﹣88×3＝96（分），此选项正确；
故选D．
本题考查了算术平均数的定义，中位数的定义，以及众数的定义，是基础题，熟记各概念是解题的关键．
4、C
【解析】
首先设，将代数式化为含有同类项的代数式，即可得解.
【详解】
设
∴
∴
故答案为C.
此题主要考查分式计算，关键是设参数求值.
5、B
【解析】
根据题意找出用电量在71～80的家庭即可．
【详解】
解：用电量在71～80的家庭有：78，74，76，76，79共5户．
故选：B．
本题主要考查了数据的收集与整理，理清题意是解题的关键．
6、C
【解析】
根据二次根式的除法法则对A进行判断；根据二次根式的乘法法则对B进行判断；根据二次根式的加减法对C进行判断；根据二次根式的性质对D进行判断．
【详解】
A、=，所以A选项的计算正确；
B、=，所以B选项的计算正确；
C、与不能合并，所以C选项的计算错误；
D、(-)2=3，所以D选项的计算正确．
故选：C．
本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后进行二次根式的乘除运算，再合并即可．
7、C
【解析】
根据勾股定理的逆定理，只要两边的平方和等于第三边的平方即可构成直角三角形．因此，只需要判断两个较小的数的平方和是否等于最大数的平方即可判断．
【详解】
解：A、92+122=152，根据勾股定理的逆定理可知是直角三角形，故选项错误；
B、52+122=132，根据勾股定理的逆定理可知是直角三角形，故选项错误；
C、32+52≠72，根据勾股定理的逆定理可知不是直角三角形，故选项正确；
D、12+=22，根据勾股定理的逆定理可知是直角三角形，故选项错误.
故选C.
本题主要考查了勾股定理的逆定理，已知三条线段的长，判断是否能构成直角三角形的三边，判断的方法是：计算两个较小的数的平方和是否等于最大数的平方即可判断．
8、C
【解析】
根据众数，中位数，平均数的定义即可解答.
【详解】
解：已知一组数据2，3，4，x，1，4，3有唯一的众数4，
只有当x=4时满足条件,
故平均数= =3，
中位数=3，
故答案选C.
本题考查众数，中位数，平均数的概念，熟悉掌握是解题关键.
二、填空题（本大题共5个小题，每小题4分，共20分）
9、1．
【解析】
设购进A种品牌衬衫a件，B种品牌衬衫b件，则C种品牌衬衫为（300﹣a﹣b）件，根据商场所获利润=A种衬衫的利润+B种衬衫的利润+C种衬衫的利润-1000，列出方程，然后根据一次函数的性质可求解.
【详解】
解：设购进A种品牌衬衫a件，B种品牌衬衫b件，则C种品牌衬衫为（300﹣a﹣b）件，获得的总利润为y元，
y＝（200﹣100）a+（350﹣200）b+（300﹣150）（300﹣a﹣b）﹣1000＝﹣50a+44000，
∵购进的每一种衬衫的数量都不少于90件，
∴a≥90，
∴当a＝90时，y取得最大值，此时y＝﹣50×90+44000＝1，
故答案为：1．
一次函数在实际生活中的应用是本题的考点，根据题意列出解析式是解题的关键.
10、2＋
【解析】
按二次根式的乘法法则求解即可.
【详解】
解：.
本题考查的是二次根式的乘法运算，熟练掌握二次根式的乘法法则是解题的关键.
11、68°
【解析】
只要证明∠EAD＝90°，想办法求出∠FAD即可解决问题.
【详解】
解：∵四边形ABCD是平行四边形，
∴∠B＝∠ADC＝66°，AD∥BC，
∵AE⊥BC，
∴AE⊥AD，
∴∠EAD＝90°，
∵F为DE的中点，
∴FA＝FD＝EF，
∵∠EDC＝44°，
∴∠ADF＝∠FAD＝22°，
∴∠EAF＝90°﹣22°＝68°，
故答案为：68°.
本题考查平行四边形的性质、直角三角形斜边中线定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
12、x1＝（x﹣4）1+（x﹣1）1
【解析】
根据题中所给的条件可知，竿斜放就恰好等于门的对角线长，可与门的宽和高构成直角三角形，运用勾股定理可求出门高、宽、对角线长．
【详解】
解：根据题意可列方程为x1＝（x﹣4）1+（x﹣1）1，
故答案为：x1＝（x﹣4）1+（x﹣1）1．
本题考查勾股定理的运用，正确运用勾股定理，将数学思想运用到实际问题中是解答本题的关键，难度一般．
13、y=-2x …（答案不唯一）
【解析】
解：答案不唯一，只要k＜0即可．如：y=-2x …．故答案为y=-2x …（答案不唯一）．
三、解答题（本大题共5个小题，共48分）
14、（1）见解析；（2）见解析；（3）ΔBEF为等腰三角形，见解析.
【解析】
（1）由平行线的性质得出∠A+∠ABC=180°，由已知得出∠C+∠ABC=180°，证出AB//BC，即可得出四边形ABCD是平行四边形；
（2）由平行四边形的性质得出BC=AD，AB//CD，得出∠CFB=∠ABF，由已知得出CF=BC，得出∠CFB=∠CBF，证出∠ABF=∠CBF即可；
（3）作FG⊥BE于G，证出FG/AD//BC，得出EG=BG，由线段垂直平分线的性质得出EF=BF即可.
【详解】
解：(1)证明：∵AD∥BC，
∴∠A+∠ABC=180°：
∵∠A=∠C
∴∠C+∠ABC=180°
∴AB∥CD
∴四边形ABCD是平行四边形
（2）证明：
∵F点为CD中点
∴CD=2CF
∴CD=2AD
∴CF=AD=BC
∴∠CFB=∠CBF
∴CD∥AB
∴∠CFB=∠FBA
∴∠FBA=∠CBF
∴BF平分∠ABC
(3)ΔBEF为等腰三角形
理由：如图，延长EF交B延长线于点G
∴DA∥BG
∴∠G=∠DEF
∵F为DC中点
∴DF=CF
又∵∠DFE=∠CFG
∴ΔDFE≌ΔCFG(AAS)
∴FE=FG
∵AD∥BC，BE⊥AD
∴BE⊥CD
∴∠EBG=90°
在RtΔEBG中，F为BG中点
∴BF=EG=EF
∴ΔBEF为等腰三角形．
本题考查了平行四边形的判定与性质、等腰三角形的判定与性质、线段垂直平分线的性质、平行线的性质等知识；熟练掌握平行四边形的判定与性质是解题的关键/
15、（1）y=x，y=2x-5（2）10
【解析】
（1）根据A点坐标即可求出y=k1x,由OA=OB得到B点坐标，即可求出一次函数y=k2x+b的关系式；（2）根据坐标与三角形的面积公式即可求解.
【详解】
（1）把A代入y=k1x,求出k1=
∴直线OA为y=x
∵OA==5，OA=OB
∴B（0,-5）
把A（4，3），B（0,-5）代入y=k2x+b求得k2=2,b=-5
∴直线AB为y=2x-5
（2）S△AOB=
此题主要考查一次函数的图像，解题的关键是数轴一次函数与几何的应用.
16、见解析
【解析】
图1，从图中可得到AC边的中点在格点上设为E，过E作AB的平行线即可在格点上找到F；图2，EC=，EF=，FC=，借助勾股定理确定F点．
【详解】
解：如图：
本题考查三角形作图；在格点中利用勾股定理，三角形的性质作平行、垂直是解题的关键．
17、（1）①见解析，②∠PCE=30°；（2）AG+EG+DG的最小值为1．
【解析】
(1)①先判断出△ABC等边三角形，得出∠ABC=60°，再由旋转知BP=BE，∠PBE=∠ABC=60°，即可得出结论．
②先用勾股定理的逆定理判断出△ACP是直角三角形，得出∠APC=90°，进而判断出∠PBE+∠PCE=90°，即可得出结论；
(2)先判断出△G'DG是等边三角形，得出GG'=DG，即：AG+EG+DG=A'G'+EG+GG'得出当A'、G'、G、E四点共线时，A'G'+EG+G'G的值最小，即可得出结论．
【详解】
解：(1)①∵四边形ABCD是菱形
∴AB=BC，
∵AC=BC，
∴AB=BC=AC，
∴△ABC等边三角形，
∴∠ABC=60°，
由旋转知BP=BE，∠CBE=∠ABP
∴∠CBE＋∠PBC=∠ABP＋∠PBC
∴∠PBE=∠ABC=60°，
∴△PBE是等边三角形；
②由①知AB=BC=1
∵由旋转知△ABP≌△CBE，
∴AP=CE=4，∠APB=∠BEC，
∵AP2+PC2=42+32=21=AC2，
∴△ACP是直角三角形，
∴∠APC=90°，
∴∠APB+∠BPC=270°，
∵∠APB=∠CEB，
∴∠CEB+∠BPC=270°，
∴∠PBE+∠PCE=360°－（∠CEB+∠BPC）=90°，
∵∠PBE=∠ABC=60°，
∴∠PCE=90°-60°=30°；
(2)如图，将△ADG绕着点D顺时针旋转60°得到△A'DG'，
由旋转知△ADG≌△A'DG'，
∴A'D=AD=4，G'D=GD，A'G'=AG，
∵∠G'DG=60°，G'D=GD，
∴△G'DG是等边三角形，
∴GG'=DG，
∴AG+EG+DG=A'G'+EG+GG'
∵当A'、G'、G、E四点共线时，A'G'+EG+G'G的值最小，
即AG+EG+DG的值最小，
∵∠A'DA=60°，∠ADE=∠ADC=30°，
∴∠A'DE=90°，
∴AG+EG+DG=A'G'+EG+G'G=A'E==1，
∴AG+EG+DG的最小值为1．
此题是四边形综合题，主要考查了等边三角形性质和判定，勾股定理，勾股定理的逆定理，旋转的性质，判断出点A'，G'，G，E四点共线时，A'G'+EG+G'G的值最小，是解本题的关键．
18、（1）15；（2）.
【解析】
(1)先进行二次根式的化简，然后再根据二次根式乘除法的运算法则进行计算即可；
(2)先分别化简各个二次根式，然后再进行合并即可.
【详解】
(1)原式=3×5÷
=15÷
=15；
(2)原式=3﹣4+
=－+.
本题考查了二次根式的混合运算，熟练掌握二次根式混合运算的运算顺序以及运算法则是解题的关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、87.1．
【解析】
根据加权平均数的含义和求法，可求出甲的平均成绩.
【详解】
面试和笔试的成绩分别为81分和90分，面试成绩和笔试成绩的权分别是1和4，
甲的平均成绩为：（分）．
故答案为：87.1．
考查加权平均数的计算，掌握加权平均数的计算方法是解题的关键.
20、1
【解析】
先求平均数，再根据方差公式求方差.
【详解】
平均数 .x=（98+99+100+101+101）=100，
方差s1= [（98-100）1+（99-100）1+（100-100）1+（101-100）1+（101-100）1]=1．
故答案为1
本题考核知识点：方差. 解题关键点：熟记方差公式.
21、-3
【解析】
分析：根据常数项为0，且二次项系数不为0列式求解即可.
详解：由题意得，
，
解之得，
m=-3.
故答案为：-3.
点睛：本题考查了一元二次方程的定义，本题的易错点是有些同学只考虑常数项为0这一条件，而忽视了二次项系数不为0这一隐含的条件.
22、6.2
【解析】
根据黄金分割的计算公式正确计算即可.
【详解】
∵点C分线段AB近似于黄金分割点（AC>BC），
∴AC=，
∵AB=10cm，
∴AC=，
故答案为：6.2.
此题考查黄金分割点的计算公式，正确掌握公式是解题的关键.
23、1
【解析】
由题意可知DE是三角形的中位线，所以DE∥BC，由平行线的性质即可求出∠ADE的度数．
【详解】
∵D，E分别为AB，AC的中点，
∴DE是三角形的中位线，
∴DE∥BC，
∴∠ADE=∠B=1°，
故答案为1．
本题考查了三角形中位线的性质以及平行线的性质．
二、解答题（本大题共3个小题，共30分）
24、（1）A商品、B商品的单价分别是50元、40元；
（2）；
（3）当购进商品少于20件，选择购B种商品省钱．
【解析】
（1）根据题意设每件A商品的单价是x元，每件B商品的单价是y元，再建立方程式进行作答.（2）根据题意建立相关的一次函数.（3）根据题意，需要分情况讨论.再利用（2）中结论，得到商品为20件时，进行分类讨论.
【详解】
（1）设每件A商品的单价是x元，每件B商品的单价是y元，由题意得
，
解得．
答：A商品、B商品的单价分别是50元、40元；
（2）当0＜x≤10时，y＝50x；
当x＞10时，y＝10×50＋（x﹣10）×50×0.6＝30x＋200；
综上所述：
（3）设购进A商品a件（a＞10），则B商品消费40a元；
当40a＝30a＋200，
则a＝20
所以当购进商品正好20件，选择购其中一种即可；
当40a＞30a＋200，
则a＞20
所以当购进商品超过20件，选择购A种商品省钱；
当40a＜30a＋200，
则a＜20
所以当购进商品少于20件，选择购B种商品省钱．
本题考查了在实际运用中方程式的建立及相关讨论，熟练掌握在实际运用中方程式的建立及相关讨论是本题解题关键.
25、（1）证明见解析；
（2）对补点如：N（，）．证明见解析
【解析】
试题分析：(1)根据正方形的对角线互相垂直,得到∠DMC＝∠AMB＝90°,从而得到点M是正方形ABCD的对补点.(2) 在直线y＝x（1＜x＜3）或直线y＝－x＋4（1＜x＜3）上
除（2，2）外的任意点均可,通过证明△DCN≌△BCN,得到∠CND＝∠CNB,利用邻补角的性质即可得出结论.
试题解析：
（1）
∵四边形ABCD是正方形，
∴ AC⊥BD．
∴ ∠DMC＝∠AMB＝90°.
即 ∠DMC＋∠AMB＝180°．
∴ 点M是正方形ABCD的对补点．
（2）对补点如：N（，）．
说明：在直线y＝x（1＜x＜3）或直线y＝－x＋4（1＜x＜3）上
除（2，2）外的任意点均可.
证明（方法一）：
连接AC ，BD
由（1）得此时对角线的交点为（2，2）．
设直线AC的解析式为：y＝kx＋b，
把点A（1，1），C（3，3）分别代入，
可求得直线AC的解析式为：y＝x．
则点N（，）是直线AC上除对角线交点外的一点，且在正方形ABCD内.
连接AC，DN，BN，
∵ 四边形ABCD是正方形，
∴ DC＝BC，∠DCN＝∠BCN．
又∵ CN＝CN，
∴ △DCN≌△BCN．
∴ ∠CND＝∠CNB．
∵ ∠CNB＋∠ANB＝180°，
∴ ∠CND＋∠ANB＝180°．
∴ 点N是正方形ABCD的对补点．
证明（方法二）：
连接AC ，BD，
由（1）得此时对角线的交点为（2，2）．
设点N是线段AC上的一点（端点A，C及对角线交点除外），
连接AC，DN，BN，
∵ 四边形ABCD是正方形，
∴ DC＝BC，∠DCN＝∠BCN．
又∵ CN＝CN，
∴ △DCN≌△BCN．
∴ ∠CND＝∠CNB．
∵ ∠CNB＋∠ANB＝180°，
∴ ∠CND＋∠ANB＝180°．
∴ 点N是正方形ABCD除对角线交点外的对补点．
设直线AC的解析式为：y＝kx＋b，
把点A（1，1），C（3，3）分别代入，可求得直线AC的解析式为：y＝x．
在1＜x＜3范围内，任取一点均为该正方形的对补点，如N（，）．
26、 (1)见解析；(2)∠BCE=∠AFD；(3)AB=m+n
【解析】
（1）将△ABD沿BD对折，使点A翻折到点C，在BD上取一点E，BE>DE，连接AE并延长交CD于F，连接CE.据此画图即可；
(2)先证出四边形ABCD是菱形，得∠BAF=∠AFD，再证出ΔABE≌ΔCBE，得到∠BCE=∠BAE.，所以∠BCE=∠AFD；
（3）由已知得出ΔACD是等边三角形，所以AD=AC, 再根据∠FAG=60°证出∠CAG=∠DAF，然后证明ΔACG≌ΔADF，得到CG=DF，从而得出AB=BC=m+n..
【详解】
(1)如图所示：
；
(2) ∠BCE=∠AFD，
理由：
由题意可知：∠ABD=∠CBD，AB=BC=AD=CD
∴四边形ABCD是菱形
∴∠BAF=∠AFD
在ΔABE和ΔCBE中
∴ΔABE≌ΔCBE（SAS）
∴∠BCE=∠BAE.
∴∠BCE=∠AFD.
(3)如图
∵四边形ABCD是菱形，∠BAD=120°，
∴∠CAD=∠CAB=60°
∴ΔACD是等边三角形
∴AD=AC
∵∠GAC+∠FAC=60°，且∠FAC+∠DAF=60°
∴∠CAG=∠DAF
在ΔACG和ΔADF中,
∴ΔACG≌ΔADF（ASA）
∴CG=DF
∵DF=n，BG=m
∴CG=n
∴BC=m+n
∴AB=BC=m+n.
本题考查了折叠问题，菱形的判定和性质以及全等三角形的判定和性质，解题时注意：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．
题号
一
二
三
四
五
总分
得分
批阅人
型号
A
B
C
进价（元/件）
100
200
150
售价（元/件）
200
350
300