

初中沪科版(2024)15.3 等腰三角形随堂练习题
展开TOC \ "1-3" \h \u
\l "_Tc5469" 【题型1 利用等腰三角形的性质求角度】 PAGEREF _Tc5469 \h 1
\l "_Tc19711" 【题型2 利用等腰三角形的性质求线段长度】 PAGEREF _Tc19711 \h 2
\l "_Tc7309" 【题型3 等腰三角形中的多结论问题】 PAGEREF _Tc7309 \h 3
\l "_Tc1458" 【题型4 利用等腰三角形的判定确定等腰三角形的个数】 PAGEREF _Tc1458 \h 4
\l "_Tc20801" 【题型5 等腰三角形的证明】 PAGEREF _Tc20801 \h 5
\l "_Tc28237" 【题型6 等腰三角形中的新定义问题】 PAGEREF _Tc28237 \h 6
\l "_Tc6643" 【题型7 等腰三角形中的规律问题】 PAGEREF _Tc6643 \h 7
\l "_Tc18646" 【题型8 等腰三角形中的动点问题】 PAGEREF _Tc18646 \h 9
【知识点1 等腰三角形】
(1)定义:有两边相等的三角形,叫做等腰三角形.
(2)等腰三角形性质
①等腰三角形的两个底角相等,即“等边对等角”;②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合(简称“三线合一”).特别地,等腰直角三角形的每个底角都等于45°.
(3)等腰三角形的判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等(即“等角对等边”).
【题型1 利用等腰三角形的性质求角度】
【例1】(2022•南关区校级开学)已知等腰三角形一腰上的高线与另一腰的夹角为60°,那么这个等腰三角形的顶角等于( )
A.15°或75°B.30°C.150°D.150°或30°
【变式1-1】(2022秋•南昌期末)如图,在△ABC中,AB=AC,∠ABM=∠CBN,MN=BN,则∠MBC的度数为( )
A.45°B.50°C.55°D.60°
【变式1-2】(2022春•柯桥区期末)在△ABC中,已知D为直线BC上一点,若∠ABC=α,∠BAD=β,且AB=AC=CD,则β与α之间不可能存在的关系式是( )
A.β=90°−32αB.β=180°−32αC.β=32α−90°D.β=120°−32α
【变式1-3】(2022春•抚州期末)已知∠ABC=30°,点P是射线BC上一动点,把△ABP沿AP折叠,B点的对应点为点D,当△ABP是等腰三角形时,∠ABD的度数为 .
【题型2 利用等腰三角形的性质求线段长度】
【例2】(2022春•源城区期末)已知等腰三角形一腰上的中线将这个等腰三角形的周长分为9cm和15cm两部分,则这个等腰三角形的腰长为( )
A.6cmB.10cmC.6cm或10cmD.11cm
【变式2-1】(2022秋•蚌埠期末)已知等腰三角形的周长是20,其中一边长为6,则其它两边的长度分别是( )
A.6和8B.7和7C.6和8或7和7D.3和11
【变式2-2】(2022春•温江区期末)如图,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,已知∠A=48°,AB+BC=15cm,求△BCF的周长和∠BFE度数.
【变式2-3】(2022秋•仓山区校级期中)如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,EC=7,求BF的长度.
【题型3 等腰三角形中的多结论问题】
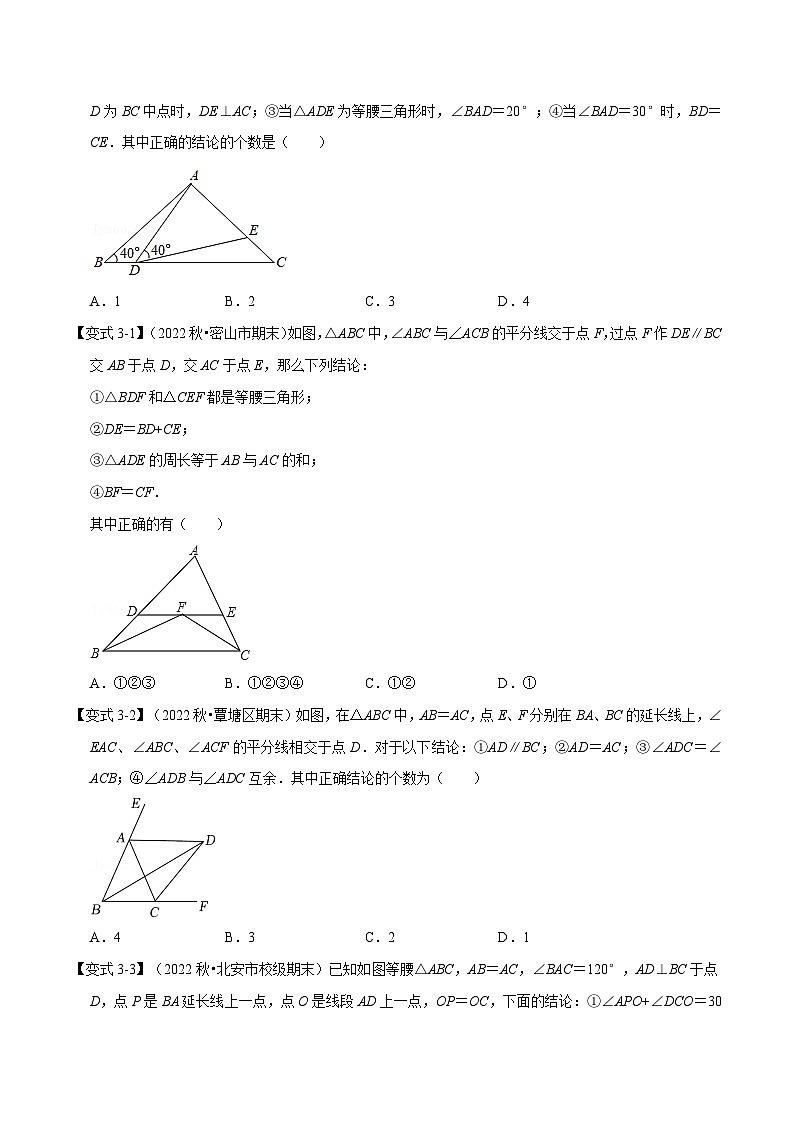
【例3】(2022秋•定陶区期末)如图,△ABC中,AB=AC,∠B=40°,D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于E,以下四个结论:①∠CDE=∠BAD;②当D为BC中点时,DE⊥AC;③当△ADE为等腰三角形时,∠BAD=20°;④当∠BAD=30°时,BD=CE.其中正确的结论的个数是( )
A.1B.2C.3D.4
【变式3-1】(2022秋•密山市期末)如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
①△BDF和△CEF都是等腰三角形;
②DE=BD+CE;
③△ADE的周长等于AB与AC的和;
④BF=CF.
其中正确的有( )
A.①②③B.①②③④C.①②D.①
【变式3-2】(2022秋•覃塘区期末)如图,在△ABC中,AB=AC,点E、F分别在BA、BC的延长线上,∠EAC、∠ABC、∠ACF的平分线相交于点D.对于以下结论:①AD∥BC;②AD=AC;③∠ADC=∠ACB;④∠ADB与∠ADC互余.其中正确结论的个数为( )
A.4B.3C.2D.1
【变式3-3】(2022秋•北安市校级期末)已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②∠APO=∠DCO;③△OPC是等边三角形;④AB=AO+AP.其中正确的是( )
A.①③④B.①②③C.①③D.①②③④
【题型4 利用等腰三角形的判定确定等腰三角形的个数】
【例4】(2022秋•顺义区期末)如图,△ABC中,直线l是边AB的垂直平分线,若直线l上存在点P,使得△PAC,△PAB均为等腰三角形,则满足条件的点P的个数共有( )
A.1B.3C.5D.7
【变式4-1】(2022秋•钟楼区期中)如图,在边长为1的小正方形网格中,A、B、C、D、Q均为格点,点P是线段AD上的一个动点,在点P运动过程中存在 个位置使得△BPQ是腰长为5的等腰三角形.
【变式4-2】(2022秋•克东县期末)如图,直线a,b相交形成的夹角中,锐角为52°,交点为O,点A在直线a上,直线b上存在点B,使以点O,A,B为顶点的三角形是等腰三角形,这样的点B有( )
A.1个B.2个C.3个D.4个
【变式4-3】(2022秋•鼓楼区校级期中)如图所示,在正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使△ABC为等腰三角形,则符合条件的点C的个数是 个.
【题型5 等腰三角形的证明】
【例5】(2022秋•镇赉县期末)如图,在△ABC中,AD平分∠BAC,E是BC上一点,BE=CD,EF∥AD交AB于F点,交CA的延长线于P,CH∥AB交AD的延长线于点H.
①求证:△APF是等腰三角形;
②猜想AB与PC的大小有什么关系?证明你的猜想.
【变式5-1】(2022秋•鄂州期末)如图,E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE,求证:△ABC是等腰三角形.
【变式5-2】(2022春•乳山市期末)如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB.
(1)求∠BPC的度数;
(2)连接EF,求证:△EFP是等腰三角形.
【变式5-3】(2022秋•海沧区期末)定义:一个三角形,若过一个顶点的线段将这个三角形分为两个三角形,其中一个是直角三角形,另一个是等腰三角形,则称这个三角形是等直三角形,这条线段叫做这个三角形的等直分割线段.
例如:
如图1,在△ABC中,
∵AD⊥BC于D,且BD=AD,
∴△ACD是直角三角形,
△ABD是等腰三角形,
∴△ABC是等直三角形,
AD是△ABC的一条等直分割线段.
(1)如图2,已知Rt△ABC中,∠C=90°,DE是AB的垂直平分线,请说明AD是△ABC的一条等直分割线段;
(2)若△ABC是一个等直三角形,恰好有两条等直分割线,∠B和∠C均小于45°,求证:△ABC是等腰三角形.
【题型6 等腰三角形中的新定义问题】
【例6】(2022春•高新区期末)定义:在一个三角形中,如果一个内角度数是另一内角度数12,我们称这样的三角形为“半角三角形”.若等腰△ABC为“半角三角形”,则△ABC的顶角度数为 .
【变式6-1】(2022秋•亳州期末)定义:过△ABC的一个顶点作一条直线m,若直线m能将△ABC恰好分成两个等腰三角形,则称△ABC为“奇妙三角形”.如图,下列标有度数的四个三角形中,不是“奇妙三角形”的是( )
A.
B.
C.
D.
【变式6-2】(2022秋•苏州期末)定义:等腰三角形的一个底角与其顶角的度数的比值k(k>1)称为这个等腰三角形的“优美比”.若在等腰三角形ABC中,∠A=36°,则它的优美比k为( )
A.32B.2C.52D.3
【变式6-3】(2022秋•海安市校级月考)定义:如果一个三角形能被过顶点的一条线段分割成两个等腰三角形,则称这个三角形为特异三角形,如图,△ABC中,∠A=36°,∠B为钝角,则使得△ABC是特异三角形所有可能的∠B的度数为 .
【题型7 等腰三角形中的规律问题】
【例7】(2022秋•咸丰县期末)等腰三角形ABC在平面直角坐标系中的位置如图所示,点A(﹣6,0),B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②,…,依此规律,第23次翻转后点C的横坐标是 .
【变式7-1】(2022秋•克东县期末)在如图①所示的钢架∠MAN中,需要焊上等长的钢条来加固钢架.若自左至右摆放,只能摆放7根,且AP1=P1P2=P2P3=…=P7P8.为了进一步加固该钢架,自点P8开始自右向左再焊上等长的钢条,如图②,且P8P9=P9P10=…=P13P14=AP14,则∠A的度数是( )
A.不存在的B.10°C.12°D.15°
【变式7-2】(2022•长春模拟)如图1,是我们平时使用的等臂圆规,即CA=CB.若n个相同规格的等臂圆规的两脚依次摆放在同一条直线上如图2所示,其张角度数变化如下:∠A1C1A2=160°,∠A2C2A3=80°,∠A3C3A4=40°,∠A4C4A5=20°,….,根据上述规律请你写出∠An+1AnCn= °.(用含n的代数式表示)
【变式7-3】(2022秋•定西期末)如图,已知∠AOB=α,在射线OA、OB上分别取点A1、B1,使OA1=OB1,连接A1B1,在A1B1、B1B上分别取点A2、B2,使B1B2=B1A2,连接A2B2,…,按此规律下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn,则θn= (2n−1)⋅180°+α2n .(用含α的式子表示)
【题型8 等腰三角形中的动点问题】
【例8】(2022秋•涪城区校级期末)如图,在等边△ABC中,AB=12cm,现有M,N两点分别从点A,B同时出发,沿△ABC的边按顺时针方向运动,已知点M的速度为1cm/s,点N的速度为2cm/s,当点N第一次到达B点时,M,N同时停止运动,设运动时间为t(s).
(1)当t为何值时,M,N两点重合?两点重合在什么位置?
(2)当点M,N在BC边上运动时,是否存在使AM=AN的位置?若存在,请求出此时点M,N运动的时间;若不存在,请说明理由.
【变式8-1】(2022春•花都区期末)“长度”和“角度”是几何学研究的核心问题.相交线与平行线的学习,让我们对“角度转化”有了深刻的体会.某数学兴趣小组受此启发,试图沟通“角度”与“长度”间的关系.在研究过程中他们发现了一条关于三角形的重要结论﹣﹣“等角对等边”,即:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
如右图,在△EBD中,若∠B=∠D,则ED=EB.
以此为基础,该兴趣小组邀请你加入研究,继续解决如下新问题:
在平面直角坐标系中,A(a,0),B(b,0),已知(a+3)2+b−3=0,点C为x轴上方的一点.
(1)如图1,若∠ABC的角平分线交AC于点D,已知点D(﹣2,2),BC上有一点E(1,2).
则①DE与x轴的位置关系为 ;
②求BE的长度;
(2)如图2,AH、BH分别平分∠CAB、∠CBA,过H点作AB的平行线,分别交AC、BC于点F、G.若F(m,n),G(m+4,n),求四边形ABGF的周长;
(3)当点C为x轴上方的一动点(不在y轴上)时,连接CA、CB.若∠CAB邻补角的角平分线和∠CBA的角平分线交于点P,过点P作AB的平行线,分别交直线AC、直线BC于点M、N.随着点C移动,图形状及点P、M、N的位置也跟着变化,但线段MN、AM和BN之间却总是存在着确定的数量关系,请直接写出这三条线段之间的数量关系 .
【变式8-2】(2022秋•定西期末)如图,在△ABC中,∠B=90°,AB=16cm,BC=12cm,AC=20cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)当点Q在边BC上运动时,出发几秒后,△PQB是等腰三角形?
(2)当点Q在边CA上运动时,出发几秒后,△BCQ是以BC或BQ为底边的等腰三角形?
【变式8-3】(2022•青羊区一模)如图,△ABC中AB=AC,BC=6,点P从点B出发沿射线BA移动,同时,点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线垂足为E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段?请说明理由.
专题15.5 等腰三角形【八大题型】
【沪科版】
TOC \ "1-3" \h \u
\l "_Tc5469" 【题型1 利用等腰三角形的性质求角度】 PAGEREF _Tc5469 \h 1
\l "_Tc19711" 【题型2 利用等腰三角形的性质求线段长度】 PAGEREF _Tc19711 \h 5
\l "_Tc7309" 【题型3 等腰三角形中的多结论问题】 PAGEREF _Tc7309 \h 8
\l "_Tc1458" 【题型4 利用等腰三角形的判定确定等腰三角形的个数】 PAGEREF _Tc1458 \h 15
\l "_Tc20801" 【题型5 等腰三角形的证明】 PAGEREF _Tc20801 \h 18
\l "_Tc28237" 【题型6 等腰三角形中的新定义问题】 PAGEREF _Tc28237 \h 24
\l "_Tc6643" 【题型7 等腰三角形中的规律问题】 PAGEREF _Tc6643 \h 27
\l "_Tc18646" 【题型8 等腰三角形中的动点问题】 PAGEREF _Tc18646 \h 29
【知识点1 等腰三角形】
(1)定义:有两边相等的三角形,叫做等腰三角形.
(2)等腰三角形性质
①等腰三角形的两个底角相等,即“等边对等角”;②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合(简称“三线合一”).特别地,等腰直角三角形的每个底角都等于45°.
(3)等腰三角形的判定
如果一个三角形有两个角相等,那么这两个角所对的边也相等(即“等角对等边”).
【题型1 利用等腰三角形的性质求角度】
【例1】(2022•南关区校级开学)已知等腰三角形一腰上的高线与另一腰的夹角为60°,那么这个等腰三角形的顶角等于( )
A.15°或75°B.30°C.150°D.150°或30°
【分析】读到此题我们首先想到等腰三角形分为锐角、直角、钝角等腰三角形,当为等腰直角三角形时不可能出现题中所说情况,所以舍去不计,我们可以通过画图来讨论剩余两种情况.
【解答】解:①当为锐角三角形时可以画图,
高与左边腰成60°夹角,由三角形内角和为180°可得,顶角为180°﹣90°﹣60°=30°,
②当为钝角三角形时可画图,
此时垂足落到三角形外面,因为三角形内角和为180°,
由图可以看出等腰三角形的顶角的补角为30°,
∴三角形的顶角为180°﹣30°=150°.
故选:D.
【变式1-1】(2022秋•南昌期末)如图,在△ABC中,AB=AC,∠ABM=∠CBN,MN=BN,则∠MBC的度数为( )
A.45°B.50°C.55°D.60°
【分析】设∠ABM=∠CBN=x,∠MBN=y,可得∠ABC=2x+y,根据MN=BN,有∠BMN=∠MBN=y,故∠A=∠BMN﹣∠ABM=y﹣x,又AB=AC,得∠C=∠ABC=2x+y,根据∠A+∠ABC+∠C=180°,得(y﹣x)+(2x+y)+(2x+y)=180°,即得x+y=60°,故∠MBC=60°.
【解答】解:设∠ABM=∠CBN=x,∠MBN=y,
∴∠ABC=2x+y,
∵MN=BN,
∴∠BMN=∠MBN=y,
∴∠A=∠BMN﹣∠ABM=y﹣x,
∵AB=AC,
∴∠C=∠ABC=2x+y,
∵∠A+∠ABC+∠C=180°,
∴(y﹣x)+(2x+y)+(2x+y)=180°,
∴3x+3y=180°,
∴x+y=60°,
∴∠CBN+∠MBN=60°,
即∠MBC=60°,
故选:D.
【变式1-2】(2022春•柯桥区期末)在△ABC中,已知D为直线BC上一点,若∠ABC=α,∠BAD=β,且AB=AC=CD,则β与α之间不可能存在的关系式是( )
A.β=90°−32αB.β=180°−32αC.β=32α−90°D.β=120°−32α
【分析】分点D在线段BC上,在BC延长线上,在CB延长线上讨论,根据外角和等于不相邻的两个内角和及三角形内角和定理可求β与α的等量关系式.
【解答】解:当点D在线段BC上,
∵∠ABC=α,CA=AB,
∴∠C=∠ABC=α,
∵CD=CA,
∴∠ADC=∠CAD=180°−∠C2=90°−12α,
∵∠ADC=∠B+∠BAD,
∴90°−12α=α+β,
即β=90°−32α;
当点D在线段BC的延长线上,
同理可得:β=180°−32α;
当点D在线段CB的延长线上,
同理可得:β=32α﹣90°.
故选:D.
【变式1-3】(2022春•抚州期末)已知∠ABC=30°,点P是射线BC上一动点,把△ABP沿AP折叠,B点的对应点为点D,当△ABP是等腰三角形时,∠ABD的度数为 60°或30°或15° .
【分析】如图1,当PA=PB时,如图2,当AB=AP时,如图3,当BA=BP时,根据三角形的内角和定理,折叠的性质,以及等腰三角形的性质分类进行讨论即可求解.
【解答】解:如图1,当PA=PB时,
∵∠ABC=30°,
∴∠BAP=30°,
∵把△ABP沿AP折叠,B点的对应点为点D,
∴AB=AD,∠DAP=∠BAP=30°,
∴∠BAD=30°+30°=60°,
∴∠ABD=60°;
如图2,当AB=AP时,
∵∠ABC=30°,
∴∠APB=30°,
∵把△ABP沿AP折叠,B点的对应点为点D,
∴PB=PD,∠DPA=∠BPA=30°,
∴∠BPD=30°+30°=60°,
∴∠PBD=60°,
∴∠ABD=60°﹣30°=30°;
如图3,当BA=BP时,
∵∠ABC=30°,
∴∠BAP=(180°﹣30°)÷2=75°,
∵把△ABP沿AP折叠,B点的对应点为点D,
∴AB=AD,∠PAB=∠PAD=75°,
∴∠BAD=75°+75°=150°,
∴∠ABD=(180°﹣150°)÷2=15°.
综上所述,当△ABP是等腰三角形时,∠ABD的度数为60°或30°或15°.
故答案为:60°或30°或15°.
【题型2 利用等腰三角形的性质求线段长度】
【例2】(2022春•源城区期末)已知等腰三角形一腰上的中线将这个等腰三角形的周长分为9cm和15cm两部分,则这个等腰三角形的腰长为( )
A.6cmB.10cmC.6cm或10cmD.11cm
【分析】已知给出的9cm和15cm两部分,没有明确哪一部分含有底边,要分类讨论,设三角形的腰为xcm,分两种情况讨论:x+12x=9或x+12x=15.
【解答】解:设三角形的腰为xcm,如图:
△ABC是等腰三角形,AB=AC,BD是AC边上的中线,
则有AB+AD=9cm或AB+AD=15cm,分下面两种情况:
(1)x+12x=9,
解得x=6,
∵三角形的周长为9+15=24(cm),
∴三边长分别为6cm,6cm,12cm,
∵6+6=12,不符合三角形的三边关系,
∴舍去;
(2)x+12x=15,
解得x=10,
∵三角形的周长为24cm,
∴三边长分别为10cm,10cm,4cm.
综上可知:这个等腰三角形的腰长为10cm.
故选:B.
【变式2-1】(2022秋•蚌埠期末)已知等腰三角形的周长是20,其中一边长为6,则其它两边的长度分别是( )
A.6和8B.7和7C.6和8或7和7D.3和11
【分析】由于长为6的边可能为腰,也可能为底边,故应分两种情况讨论.
【解答】解:当腰为6时,另一腰也为6,则底为20﹣2×6=8,
∵6+6=12>8,
∴三边能构成三角形.
当底为6时,腰为(20﹣6)÷2=7,
∵7+7>6,
∴三边能构成三角形.
故选:C.
【变式2-2】(2022春•温江区期末)如图,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,已知∠A=48°,AB+BC=15cm,求△BCF的周长和∠BFE度数.
【分析】由在△ABC中,AB=AC,∠A=48°,根据等腰三角形的性质,可求得∠ABC=∠ACB=66°,又由AB的垂直平分线DE交BC的延长线于E,交AC于F,可求得∠ABF的度数,继而求得∠BFE的度数,易得△BCF的周长=BC+AC=BC+AB.
【解答】解:∵在△ABC中,AB=AC,∠A=48°,
∴∠ABC=∠ACB=66°,
∵DE是AB的垂直平分线,
∴AF=BF,∠BDE=90°,∠ABF=∠A=48°,
∴∠BFD=90°﹣∠ABF=42°,
∴∠BFE=138°;
∵AB+BC=15cm,
∴△BCF的周长为:BC+CF+BF=BC+CF+AF=BC+AC=BC+AB=15cm.
【变式2-3】(2022秋•仓山区校级期中)如图,在△ABC中,AB=AC,点E在CA延长线上,EP⊥BC于点P,交AB于点F,若AF=2,EC=7,求BF的长度.
【分析】根据等边对等角得出∠B=∠C,再根据EP⊥BC,得出∠C+∠E=90°,∠B+∠BFP=90°,从而得出∠E=∠BFP,再根据对顶角相等得出∠E=∠AFE,最后根据等角对等边即可得出答案.
【解答】解:在△ABC中,AB=AC,
∴∠B=∠C,
∵EP⊥BC,
∴∠C+∠E=90°,∠B+∠BFP=90°,
∴∠E=∠BFP,
又∵∠BFP=∠AFE,
∴∠E=∠AFE,
∴AE=AF=2,
∴△AEF是等腰三角形.
又∵CE=7,
∴AB=AC=CE﹣AE=7﹣2=5,
∴BF=AB﹣AF=5﹣2=3.
【题型3 等腰三角形中的多结论问题】
【例3】(2022秋•定陶区期末)如图,△ABC中,AB=AC,∠B=40°,D为线段BC上一动点(不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于E,以下四个结论:①∠CDE=∠BAD;②当D为BC中点时,DE⊥AC;③当△ADE为等腰三角形时,∠BAD=20°;④当∠BAD=30°时,BD=CE.其中正确的结论的个数是( )
A.1B.2C.3D.4
【分析】根据等腰三角形的性质得到∠B=∠C=40°,根据三角形的内角和和平角的定义即可得到∠BAD=∠CDE;根据等腰三角形的性质得到AD⊥BC,根据三角形的内角和即可得到DE⊥AC;根据三角形外角的性质得到∠AED>40°,求得∠ADE≠∠AED,根据等腰三角形的性质和三角形的内角和得到∠BAD=60°,根据全等三角形的性质得到BD=CE.
【解答】解:①∵AB=AC,
∴∠B=∠C=40°,
∴∠BAD=180°﹣40°﹣∠ADB,∠CDE=180°﹣40°﹣∠ADB,
∴∠BAD=∠CDE;故①正确;
②∵D为BC中点,AB=AC,
∴AD⊥BC,
∴∠ADC=90°,
∴∠CDE=50°,
∵∠C=40°,
∴∠DEC=90°,
∴DE⊥AC,故②正确;
③∵∠C=40°,
∴∠AED>40°,
∴∠ADE≠∠AED,
∵△ADE为等腰三角形,
∴AE=DE,
∴∠DAE=∠ADE=40°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=60°,
或∵△ADE为等腰三角形,
∴AD=DE,
∴∠DAE=∠AED=70°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=30°,
故③错误,
④∵∠BAD=30°,
∴∠CDE=30°,
∴∠ADC=70°,
∴∠CAD=180°﹣70°﹣40°=70°,
∴∠DAC=∠ADC,
∴CD=AC,
∵AB=AC,
∴CD=AB,
∴△ABD≌△DCE(ASA),
∴BD=CE;故④正确;
故选:C.
【变式3-1】(2022秋•密山市期末)如图,△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D,交AC于点E,那么下列结论:
①△BDF和△CEF都是等腰三角形;
②DE=BD+CE;
③△ADE的周长等于AB与AC的和;
④BF=CF.
其中正确的有( )
A.①②③B.①②③④C.①②D.①
【分析】由平行线得到角相等,由角平分线得角相等,根据平行线的性质及等腰三角形的判定和性质.
【解答】解:∵DE∥BC,
∴∠DFB=∠FBC,∠EFC=∠FCB,
∵BF是∠ABC的平分线,CF是∠ACB的平分线,
∴∠FBC=∠DFB,∠FCE=∠FCB,
∵∠DBF=∠DFB,∠EFC=∠ECF,
∴△DFB,△FEC都是等腰三角形.
∴DF=DB,FE=EC,即有DE=DF+FE=DB+EC,
∴△ADE的周长AD+AE+DE=AD+AE+DB+EC=AB+AC.
故选:A.
【变式3-2】(2022秋•覃塘区期末)如图,在△ABC中,AB=AC,点E、F分别在BA、BC的延长线上,∠EAC、∠ABC、∠ACF的平分线相交于点D.对于以下结论:①AD∥BC;②AD=AC;③∠ADC=∠ACB;④∠ADB与∠ADC互余.其中正确结论的个数为( )
A.4B.3C.2D.1
【分析】①由∠EAC是△ABC的外角得到∠EAC=∠ABC+∠ACB,由AB=AC得到∠ABC=∠ACB,进而得到∠EAC=2∠ABC,然后由AD平分∠EAC得到∠EAC=2∠EAD,从而得到∠EAD=∠ABC,最后得到AD∥BC;
②由AD∥BC得到∠ADC=∠DCF,再由CD平分∠ACF得到∠ACD=∠DCF,进而得到∠ACD=∠ADC,即得AC=AD;
③由∠ADC=∠ACD=∠DCF得到∠ADC=12∠ACF,再由∠ACF=180°﹣∠ACB得到∠ADC与∠ACB的数量关系;
④由AD∥BC得到∠ADB=∠DBC,再由BD平分∠ABC得到∠ADB=12∠ABC,结合∠ADC=12∠ACF得到∠ADB+∠ADC=12∠ABC+12∠ACF,再由∠ABC=∠ACB,∠ACB+∠ACF=180°得到∠ADB+∠ADC=90°,即可得到∠ADB与∠ADC互余.
【解答】解:①∵∠EAC是△ABC的外角,
∴∠EAC=∠ABC+∠ACB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EAC=2∠ABC,
∵AD平分∠EAC,
∴∠EAC=2∠EAD,
∴∠EAD=∠ABC,
∴AD∥BC,故①正确,符合题意;
②∵AD∥BC,
∴∠ADC=∠DCF,
∵CD平分∠ACF,
∴∠ACD=∠DCF,
∴∠ACD=∠ADC,
∴AC=AD,故②正确,符合题意;
③∵∠ADC=∠ACD=∠DCF,
∴∠ADC=12∠ACF,
∵∠ACF=180°﹣∠ACB,
∴∠ADC=12(180°﹣∠ACB)=90°−12∠ACB,故③错误,不符合题意;
④∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ADB=12∠ABC,
∵∠ADC=12∠ACF,
∴∠ADB+∠ADC=12∠ABC+12∠ACF,
∵∠ABC=∠ACB,∠ACB+∠ACF=180°,
∴∠ADB+∠ADC=90°,
∴∠ADB与∠ADC互余,故④正确,符合题意,
∴正确的结论个数有3个,
故选:B.
【变式3-3】(2022秋•北安市校级期末)已知如图等腰△ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论:①∠APO+∠DCO=30°;②∠APO=∠DCO;③△OPC是等边三角形;④AB=AO+AP.其中正确的是( )
A.①③④B.①②③C.①③D.①②③④
【分析】①利用等边对等角,即可证得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;
②因为点O是线段AD上一点,所以BO不一定是∠ABD的角平分线,可作判断;
③证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形;
④首先证明△OPA≌△CPE,则AO=CE,AB=AC=AE+CE=AO+AP.
【解答】解:①如图1,连接OB,
∵AB=AC,AD⊥BC,
∴BD=CD,∠BAD=12∠BAC=12×120°=60°,
∴OB=OC,∠ABC=90°﹣∠BAD=30°
∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DCO=∠DBO,
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;
故①正确;
②由①知:∠APO=∠ABO,∠DCO=∠DBO,
∵点O是线段AD上一点,
∴∠ABO与∠DBO不一定相等,则∠APO与∠DCO不一定相等,
故②不正确;
③∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°﹣(∠OPC+∠OCP)=60°,
∵OP=OC,
∴△OPC是等边三角形;
故③正确;
④如图2,在AC上截取AE=PA,连接PE,
∵∠PAE=180°﹣∠BAC=60°,
∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
∵OP=CP,
在△OPA和△CPE中,
PA=PE∠APO=∠CPEOP=CP,
∴△OPA≌△CPE(SAS),
∴AO=CE,
∴AB=AC=AE+CE=AO+AP;
故④正确;
本题正确的结论有:①③④
故选:A.
【题型4 利用等腰三角形的判定确定等腰三角形的个数】
【例4】(2022秋•顺义区期末)如图,△ABC中,直线l是边AB的垂直平分线,若直线l上存在点P,使得△PAC,△PAB均为等腰三角形,则满足条件的点P的个数共有( )
A.1B.3C.5D.7
【分析】分三种情况,AP=AC,CA=CP,PA=PC.
【解答】解:分三种情况:如图:
当AP=AC时,以A为圆心,AC长为半径画圆,交直线l于点P1,P2,
当CA=CP时,以C为圆心,CA长为半径画圆,交直线l于点P3,P4,
当PA=PC时,作AC的垂直平分线,交直线l于点P5,
∵直线l是边AB的垂直平分线,
∴直线l上任意一点(与AB的交点除外)与AB构成的三角形均为等腰三角形,
∴满足条件的点P的个数共有5个,
故选:C.
【变式4-1】(2022秋•钟楼区期中)如图,在边长为1的小正方形网格中,A、B、C、D、Q均为格点,点P是线段AD上的一个动点,在点P运动过程中存在 3 个位置使得△BPQ是腰长为5的等腰三角形.
【分析】根据等腰三角形的定义,画出图形判定即可.
【解答】解:如图,满足条件的等腰三角形有3个.
故答案为:3.
【变式4-2】(2022秋•克东县期末)如图,直线a,b相交形成的夹角中,锐角为52°,交点为O,点A在直线a上,直线b上存在点B,使以点O,A,B为顶点的三角形是等腰三角形,这样的点B有( )
A.1个B.2个C.3个D.4个
【分析】根据△OAB为等腰三角形,分三种情况讨论:①当OB=AB时,②当OA=AB时,③当OA=OB时,分别求得符合的点B,即可得解.
【解答】解:要使△OAB为等腰三角形分三种情况讨论:
①当OB=AB时,作线段OA的垂直平分线,与直线b的交点为B,此时有1个;
②当OA=AB时,以点A为圆心,OA为半径作圆,与直线b的交点,此时有1个;
③当OA=OB时,以点O为圆心,OA为半径作圆,与直线b的交点,此时有2个,
1+1+2=4,
故选:D.
【变式4-3】(2022秋•鼓楼区校级期中)如图所示,在正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使△ABC为等腰三角形,则符合条件的点C的个数是 8 个.
【分析】根据等腰三角形的性质分三种情况:AB为底边,C点在AB的垂直平分线上;AB为腰且∠A为顶角时,AB为腰且∠B为顶角时,分别判定可求解.
【解答】解:如图所示:
∴符合条件的点C的个数为8.
故答案为8.
【题型5 等腰三角形的证明】
【例5】(2022秋•镇赉县期末)如图,在△ABC中,AD平分∠BAC,E是BC上一点,BE=CD,EF∥AD交AB于F点,交CA的延长线于P,CH∥AB交AD的延长线于点H.
①求证:△APF是等腰三角形;
②猜想AB与PC的大小有什么关系?证明你的猜想.
【分析】①根据题意作出图形,根据两直线平行,内错角相等可得∠1=∠4,同位角相等可得∠2=∠P,再根据角平分线的定义可得∠1=∠2,然后求出∠4=∠P,根据等角对等边的性质即可得证;
②根据两直线平行,内错角相等可得∠5=∠B,再求出∠H=∠1=∠3,然后利用“AAS”证明△BEF和△CDH全等,根据全等三角形对应边相等可得BF=CH,再求出AC=CH,再根据AB=AF+BF,PC=AP+AC,整理即可得解.
【解答】①证明:∵EF∥AD,
∴∠1=∠4,∠2=∠P,
∵AD平分∠BAC,
∴∠1=∠2,
∴∠4=∠P,
∴AF=AP,
即△APF是等腰三角形;
②AB=PC.理由如下:
证明:∵CH∥AB,
∴∠5=∠B,∠H=∠1,
∵EF∥AD,
∴∠1=∠3,
∴∠H=∠3,
在△BEF和△CDH中,
∵∠5=∠B∠H=∠3BE=CD,
∴△BEF≌△CDH(AAS),
∴BF=CH,
∵AD平分∠BAC,
∴∠1=∠2,
∴∠2=∠H,
∴AC=CH,
∴AC=BF,
∵AB=AF+BF,PC=AP+AC,
∴AB=PC.
【变式5-1】(2022秋•鄂州期末)如图,E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE,求证:△ABC是等腰三角形.
【分析】利用平行线的性质得出∠GDF=∠CEF进而利用ASA得出△GDF≌△CEF,再利用全等三角形的性质以及等腰三角形的判定得出即可.
【解答】证明:过点D作DG∥AE于点G,
∵DG∥AC
∴∠GDF=∠CEF(两直线平行,内错角相等),
在△GDF和△CEF中
∠GDF=∠CEFDF=EF∠DFG=∠CFE,
∴△GDF≌△CEF(ASA),
∴DG=CE
又∵BD=CE,
∴BD=DG,
∴∠DBG=∠DGB,
∵DG∥AC,
∴∠DGB=∠ACB,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
【变式5-2】(2022春•乳山市期末)如图,在△ABC中,∠A=60°.BE,CF交于点P,且分别平分∠ABC,∠ACB.
(1)求∠BPC的度数;
(2)连接EF,求证:△EFP是等腰三角形.
【分析】(1)根据三角形内角和定理得出∠ABC+∠ACB=180°﹣∠A=120°,根据角平分线定义得出∠ABE=∠CBE=12∠ABC,∠BCF=∠ACF=12∠ACB,求出∠CBE+∠BCF=12∠ABC+12∠ACB=60°,再根据三角形内角和定理求出答案即可;
(2)在BC上截取BQ=BF,连接PQ,根据全等三角形的判定得出△FBP≌△QBP,根据全等三角形的性质得出FP=QP,∠BFP=∠BQP,求出∠CEP=∠CQP,根据全等三角形的判定得出△CQP≌△CEP,根据全等三角形的性质得出EF=QP,求出FP=EP即可.
【解答】(1)解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=120°,
∵BE平分∠ABC,CF平分∠ACB,
∴∠ABE=∠CBE=12∠ABC,∠BCF=∠ACF=12∠ACB,
∴∠CBE+∠BCF=12∠ABC+12∠ACB=12×120°=60°,
∴∠BPC=180°﹣(∠CBE+∠BCF)=180°﹣60°=120°;
(2)证明:在BC上截取BQ=BF,连接PQ,
在△FBP和△QBP中,
BP=BP∠FBP=∠QBPBF=BQ,
∴△FBP≌△QBP(SAS),
∴FP=QP,∠BFP=∠BQP,
∵∠A=60°,∠FPE=∠BPC=120°,
∴∠AFP+∠AEP=360°﹣60°﹣120°=180°,
∴∠BFP+∠CEP=180°,
∵∠CQP+∠BQP=180°,
∴∠CEP=∠CQP,
在△CQP和△CEP中,
∠QCP=∠ECP∠CQP=∠CEPCP=CP,
∴△CQP≌△CEP(AAS),
∴EF=QP,
∵FP=EP,
∴△EFP是等腰三角形.
【变式5-3】(2022秋•海沧区期末)定义:一个三角形,若过一个顶点的线段将这个三角形分为两个三角形,其中一个是直角三角形,另一个是等腰三角形,则称这个三角形是等直三角形,这条线段叫做这个三角形的等直分割线段.
例如:
如图1,在△ABC中,
∵AD⊥BC于D,且BD=AD,
∴△ACD是直角三角形,
△ABD是等腰三角形,
∴△ABC是等直三角形,
AD是△ABC的一条等直分割线段.
(1)如图2,已知Rt△ABC中,∠C=90°,DE是AB的垂直平分线,请说明AD是△ABC的一条等直分割线段;
(2)若△ABC是一个等直三角形,恰好有两条等直分割线,∠B和∠C均小于45°,求证:△ABC是等腰三角形.
【分析】(1)利用线段垂直平分线的性质可得AD=BD,可证明结论;
(2)根据等值分割线的定义画出图形,可证明∠BAD=∠CAE,从而得出∠B=∠C,可证明结论.
【解答】证明:(1)∵DE是AB的垂直平分线,
∴AD=BD,
∴△ABD是等腰三角形,
又∵∠C=90°,
∴△ACD是直角三角形,
∴AD是△ABC的一条等直分割线段;
(2)如图,AD,AE是△ABC的两条等值分割线段,
∴AD=BD,∠BAE=90°,AE=CE,∠CAD=90°,
∴∠B=∠BAD,∠C=∠CAE,
∵∠BAE=∠BAD+∠DAE=90°,
∠CAD=∠DAE+∠CAE=90°,
∴∠BAD=∠CAE,
∴∠B=∠C,
∴△ABC是等腰三角形.
【题型6 等腰三角形中的新定义问题】
【例6】(2022春•高新区期末)定义:在一个三角形中,如果一个内角度数是另一内角度数12,我们称这样的三角形为“半角三角形”.若等腰△ABC为“半角三角形”,则△ABC的顶角度数为 36°或90° .
【分析】分两种情况讨论:顶角度数是底角度数12;底角度数是顶角度数12;进行计算即可求解.
【解答】解:顶角度数是底角度数12,
顶角:180°÷(2+2+1)=36°;
底角度数是顶角度数12,
顶角:180°÷(12+12+1)=90°.
故△ABC的顶角度数为36°或90°.
故答案为:36°或90°.
【变式6-1】(2022秋•亳州期末)定义:过△ABC的一个顶点作一条直线m,若直线m能将△ABC恰好分成两个等腰三角形,则称△ABC为“奇妙三角形”.如图,下列标有度数的四个三角形中,不是“奇妙三角形”的是( )
A.
B.
C.
D.
【分析】根据等腰三角形的定义画出图形即可判断.
【解答】解:A.是“奇妙三角形”,不合题意;
B.是“奇妙三角形”,不合题意;
C.不是“奇妙三角形”,符合题意;
D.是“奇妙三角形”,不合题意;
故选:C.
【变式6-2】(2022秋•苏州期末)定义:等腰三角形的一个底角与其顶角的度数的比值k(k>1)称为这个等腰三角形的“优美比”.若在等腰三角形ABC中,∠A=36°,则它的优美比k为( )
A.32B.2C.52D.3
【分析】分两种情况:∠A为顶角或∠A为底角,再根据三角形内角和定理可求得底角或顶角的度数,即可得到它的优美比k.
【解答】解:当∠A为顶角时,则底角∠B=72°;
此时,优美比k=72°36°=2;
当∠A为底角时,则顶角为108°;
此时,优美比k=36°108°=13(k<1,不合题意,舍去);
故选:B.
【变式6-3】(2022秋•海安市校级月考)定义:如果一个三角形能被过顶点的一条线段分割成两个等腰三角形,则称这个三角形为特异三角形,如图,△ABC中,∠A=36°,∠B为钝角,则使得△ABC是特异三角形所有可能的∠B的度数为 108°或126°或132° .
【分析】利用特异三角形得到△ABD和△CBD都是等腰三角形,讨论:①当AB=AD时,利用等腰三角形的性质和三角形内角和定理可计算出∠ABD=∠ADB=12=72°,若DB=DC,利用等腰三角形的性质和三角形外角性质可计算∠C=∠CBD=12∠ADB=36°,从而得到∠ABC=108°;由于∠CDB=108°,根据三角形内角和可判断CD=CB与BD=BC不成立;②当DA=DB,利用等腰三角形性质得∠ABD=∠A=36°,根据三角形外角性质得∠CDB=72°,若DB=DC,则∠C=∠CBD=54°,此时∠ABC=90°,不合题意舍去;若CD=CB,则∠CBD=∠CDB=72°,此时∠ABC=108°;③当BA=BD时,则∠ADB=∠A=36°,易得∠ABD=108°,若DB=DC,则∠C=∠CBD=12∠ADB=18°,此时∠ABC=126°;由于∠CDB=144°,利用三角形内角和可判断则CD=CB或BD=BC不成立;④当BA=BD,DA=DC,
设∠BAD=x,则∠ADB=x,根据三角形外角性质得∠C=∠DAC=12x,所以x+12x=36°,解得x=24°,从而得到∠B=132°;综上所述,∠B的度数为108°或126°或132°.
【解答】解:∵△ABC是特异三角形,
∴△ABD和△CBD都是等腰三角形,
①当AB=AD时,则∠ABD=∠ADB=12(180°﹣∠A)=12(180°﹣36°)=72°,
若DB=DC,则∠C=∠CBD=12∠ADB=36°,
此时∠ABC=72°+36°=108°;
由于∠CDB=108°,则CD=CB与BD=BC不成立;
②当DA=DB,则∠ABD=∠A=36°,所以∠CDB=36°+36°=72°,
若DB=DC,则∠C=∠CBD=12(180°﹣72°)=54°,此时∠ABC=54°+36°=90°,不合题意舍去;
若CD=CB,则∠CBD=∠CDB=72°,此时∠ABC=72°+36°=108°;
③当BA=BD时,则∠ADB=∠A=36°,∠ABD=180°﹣36°﹣36°=108°,
若DB=DC,则∠C=∠CBD=12∠ADB=18°,此时∠ABC=108°+18°=126°;
由于∠CDB=144°,则CD=CB与BD=BC不成立;
④当BA=BD,DA=DC,
设∠BAD=x,则∠ADB=x,
∵DC=DA,
∴∠C=∠DAC=12x,
∴x+12x=36°,解得x=24°,
∴∠B=180°﹣24°﹣24°=132°;
综上所述,∠B的度数为108°或126°或132°.
故答案为108°或126°或132°.
【题型7 等腰三角形中的规律问题】
【例7】(2022秋•咸丰县期末)等腰三角形ABC在平面直角坐标系中的位置如图所示,点A(﹣6,0),B在原点,CA=CB=5,把等腰三角形ABC沿x轴正半轴作无滑动顺时针翻转,第一次翻转到位置①,第二次翻转到位置②,…,依此规律,第23次翻转后点C的横坐标是 117 .
【分析】根据题意可知每翻折三次与初始位置的形状相同,第24次与开始时形状相同,可先求第24次的坐标,再求出第23次翻转后点C的横坐标即可;
【解答】解:由题意可得,每翻转三次与初始位置的形状相同,
翻转3次后C点的纵坐标不变,横坐标的变化为:5+5+3+3,
故第24次翻转后点C的横坐标是:﹣3+(3+5+5+3)×8=125,
∴第23次翻转后点C的横坐标是125﹣8=117,
故答案为:117.
【变式7-1】(2022秋•克东县期末)在如图①所示的钢架∠MAN中,需要焊上等长的钢条来加固钢架.若自左至右摆放,只能摆放7根,且AP1=P1P2=P2P3=…=P7P8.为了进一步加固该钢架,自点P8开始自右向左再焊上等长的钢条,如图②,且P8P9=P9P10=…=P13P14=AP14,则∠A的度数是( )
A.不存在的B.10°C.12°D.15°
【分析】设∠A=x,根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和求出∠AP7P8,∠AP8P7,再根据三角形的内角和定理列式进行计算即可得解.
【解答】解:设∠A=x,
∵AP1=P1P2==P13P14=P14A,
∴∠A=∠AP2P1=∠AP13P14=x,
∴∠P2P1P3=∠P13P14P12=2x,
∴∠P3P2P4=∠P12P13P11=3x,
,
∠P7P6P8=∠P8P9P7=7x,
∴∠AP7P8=7x,∠AP8P7=7x,
在△AP7P8中,∠A+∠AP7P8+∠AP8P7=180°,
即x+7x+7x=180°,
解得x=12°,
【变式7-2】(2022•长春模拟)如图1,是我们平时使用的等臂圆规,即CA=CB.若n个相同规格的等臂圆规的两脚依次摆放在同一条直线上如图2所示,其张角度数变化如下:∠A1C1A2=160°,∠A2C2A3=80°,∠A3C3A4=40°,∠A4C4A5=20°,….,根据上述规律请你写出∠An+1AnCn= (90−802n−1) °.(用含n的代数式表示)
【分析】利用三角形的内角和计算,同时注意利用等腰三角形的性质.
【解答】解:由张角度数变化可知顶角∠An+1CnAn=(1602n−1)°,
则∠An+1AnCn=(180−1602n−1)°÷2=(90−802n−1)°.
故答案为:(90−802n−1).
【变式7-3】(2022秋•定西期末)如图,已知∠AOB=α,在射线OA、OB上分别取点A1、B1,使OA1=OB1,连接A1B1,在A1B1、B1B上分别取点A2、B2,使B1B2=B1A2,连接A2B2,…,按此规律下去,记∠A2B1B2=θ1,∠A3B2B3=θ2,…,∠An+1BnBn+1=θn,则θn= (2n−1)⋅180°+α2n .(用含α的式子表示)
【分析】设∠A1B1O=x,根据等腰三角形性质和三角形内角和定理得α+2x=180°,x=180°﹣θ1,即可求得θ1=180°+α2,同理求得θ2=180°+θ12,即可发现其中的规律,按照此规律即可求得答案.
【解答】解:设∠A1B1O=x,
则α+2x=180°,x=180°﹣θ1,
∴θ1=180°+α2,
设∠A2B2B1=y,
则θ2+y=180°①,θ1+2y=180°②,
①×2﹣②得:2θ2﹣θ1=180°,
∴θ2=180°+θ12=(22−1)⋅180°+α22,
…
θn=(2n−1)⋅180°+α2n.
故答案为:(2n−1)⋅180°+α2n.
【题型8 等腰三角形中的动点问题】
【例8】(2022秋•涪城区校级期末)如图,在等边△ABC中,AB=12cm,现有M,N两点分别从点A,B同时出发,沿△ABC的边按顺时针方向运动,已知点M的速度为1cm/s,点N的速度为2cm/s,当点N第一次到达B点时,M,N同时停止运动,设运动时间为t(s).
(1)当t为何值时,M,N两点重合?两点重合在什么位置?
(2)当点M,N在BC边上运动时,是否存在使AM=AN的位置?若存在,请求出此时点M,N运动的时间;若不存在,请说明理由.
【分析】(1)首先根据M、N两点重合,表示出M,N的运动路程,N的运动路程比M的运动路程多12cm,列出方程求解即可;
(2)首先假设△AMN是等腰三角形,可证出△ACM≌△ABN,可得CM=BN,设出运动时间,表示出CM,NB,NM的长,列出方程,可解出未知数的值.
【解答】解:(1)由题意,t×1+12=2t,
解得:t=12,
∴当t=12时,M,N两点重合,
此时两点在点C处重合;
(2)结论:当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形.
理由:由(1)知12秒时M、N两点重合,恰好在C处,
如图,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
∠C=∠B∠AMC=∠ANBAC=AB,
∴△ACM≌△ABN(AAS),
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y﹣12,NB=36﹣2y,
∵CM=NB,
∴y﹣12=36﹣2y,
解得:y=16.故假设成立.
∴当点M、N在BC边上运动时,当运动时间为12秒或16秒时,AM=AN.
【变式8-1】(2022春•花都区期末)“长度”和“角度”是几何学研究的核心问题.相交线与平行线的学习,让我们对“角度转化”有了深刻的体会.某数学兴趣小组受此启发,试图沟通“角度”与“长度”间的关系.在研究过程中他们发现了一条关于三角形的重要结论﹣﹣“等角对等边”,即:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
如右图,在△EBD中,若∠B=∠D,则ED=EB.
以此为基础,该兴趣小组邀请你加入研究,继续解决如下新问题:
在平面直角坐标系中,A(a,0),B(b,0),已知(a+3)2+b−3=0,点C为x轴上方的一点.
(1)如图1,若∠ABC的角平分线交AC于点D,已知点D(﹣2,2),BC上有一点E(1,2).
则①DE与x轴的位置关系为 平行 ;
②求BE的长度;
(2)如图2,AH、BH分别平分∠CAB、∠CBA,过H点作AB的平行线,分别交AC、BC于点F、G.若F(m,n),G(m+4,n),求四边形ABGF的周长;
(3)当点C为x轴上方的一动点(不在y轴上)时,连接CA、CB.若∠CAB邻补角的角平分线和∠CBA的角平分线交于点P,过点P作AB的平行线,分别交直线AC、直线BC于点M、N.随着点C移动,图形状及点P、M、N的位置也跟着变化,但线段MN、AM和BN之间却总是存在着确定的数量关系,请直接写出这三条线段之间的数量关系 BN=AM+MN .
【分析】(1)①由两点的纵坐标相同,可得DE∥BA;②由平行线的性质和角平分线的性质可得∠EDB=∠EBD,即可求DE=BE=3;
(2)利用非负性可求a=﹣3,b=3,可得AB=6,由平行线的性质和角平分线的性质可得∠FAH=∠FHA,∠GHB=∠GBH,可证AF=FH,BG=HG,可求解;
(3)由平行线的性质和角平分线的性质可得∠NPA=∠PAC,∠NPB=∠PBN,可证PM=AM,BN=PN,由线段的和差关系可得结论.
【解答】解:(1)①∵点D(﹣2,2),点E(1,2),
∴DE∥AB,DE=3,
故答案为平行;
②∵DE∥AB,
∴∠EDB=∠DBA,
∵DB平分∠ABC,
∴∠ABD=∠DBE,
∴∠EDB=∠EBD,
∴DE=BE=3;
(2)∵(a+3)2+b−3=0,
∴a=﹣3,b=3,
∴点A(﹣3,0),B(3,0),
∴AB=6,
∵F(m,n),G(m+4,n),
∴FG=4,FG∥AB,
∴∠FHA=∠HAB,∠GHB=∠ABH,
∵AH、BH分别平分∠CAB、∠CBA,
∴∠FAH=∠HAB,∠GBH=∠ABH,
∴∠FAH=∠FHA,∠GHB=∠GBH,
∴AF=FH,BG=HG,
∴四边形ABGF的周长=AB+AF+FH+HG+BG=AB+2FG=14;
(3)点C在第一象限时,BN=AM+MN,理由如下,
如图3,
∵PA平分∠CAE,PB平分∠ABC,
∴∠PAE=∠PAC,∠PBA=∠PBC,
∵PN∥AB,
∴∠NPB=∠PBA,∠NPA=∠PAE,
∴∠NPA=∠PAC,∠NPB=∠PBN,
∴PM=AM,BN=PN,
∵PN=PM+MN,
∴BN=AM+MN.
当点C在第一象限,AM=BN+MN,同理可证.
【变式8-2】(2022秋•定西期末)如图,在△ABC中,∠B=90°,AB=16cm,BC=12cm,AC=20cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)当点Q在边BC上运动时,出发几秒后,△PQB是等腰三角形?
(2)当点Q在边CA上运动时,出发几秒后,△BCQ是以BC或BQ为底边的等腰三角形?
【分析】(1)用t可分别表示出BP和BQ,根据等腰三角形的性质可得到BP=BQ,可得到关于t的方程,可求得t;
(2)用t分别表示出BQ和CQ,利用等腰三角形的性质可分CQ=BC和BQ=CQ三种情况,分别得到关于t的方程,可求得t的值.
【解答】解:(1)由题意可知AP=t,BQ=2t,
∵AB=16,
∴BP=AB﹣AP=16﹣t,
当△PQB为等腰三角形时,则有BP=BQ,
即16﹣t=2t,解得t=163,
∴出发163秒后△PQB能形成等腰三角形;
(2)①当△BCQ是以BC为底边的等腰三角形时:CQ=BQ,如图1所示,
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°.
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=10(cm),
∴BC+CQ=22(cm),
∴t=22÷2=11(秒).
②当,△BCQ是以BQ为底边的等腰三角形时:CQ=BC,如图2所示,
则BC+CQ=24(cm),
∴t=24÷2=12(秒).
综上所述:当t为11秒或12秒时,△BCQ是以BC或BQ为底边的等腰三角形.
【变式8-3】(2022•青羊区一模)如图,△ABC中AB=AC,BC=6,点P从点B出发沿射线BA移动,同时,点Q从点C出发沿线段AC的延长线移动,已知点P、Q移动的速度相同,PQ与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线垂足为E,当点P、Q在移动的过程中,线段BE、DE、CD中是否存在长度保持不变的线段?请说明理由.
【分析】(1)过点P做PF平行于AQ,由平行我们得出一对同位角和一对内错角的相等,再由AB=AC,根据等边对等角得角B和角ACB的相等,根据等量代换的角B和角PFB的相等,根据等角对等边得BP=PF,又因点P和点Q同时出发,且速度相同即BP=CQ,等量代换得PF=CQ,在加上对等角的相等,证得三角形PFD和三角形QCD的全等,根据全等三角形的对应边边相等得出DF=CD=12CF,而又因P是AB的中点,PF∥AQ得出F是BC的中点,进而根据已知的BC的长,求出CF,即可得出CD的长.
(2)分两种情况讨论,第一种情况点P在线段AB上,根据等腰三角形的三线合一得BE=EF,再又第一问的全等可知DF=CD,所以ED=EF+FD=BE+DC=12BC=3,得出线段DE的长为定值;第二种情况,P在BA的延长线上,作PM平行于AC交BC的延长线于M,根据两直线平行,同位角相等推出角PMB等于角ACB,而角ACB等于角ABC,根据等量代换得到角ABC等于角PMB,根据等角对等边得到PM等于PB,根据三线合一,得到BE等于EM,同理可得△PMD全等于△QCD,得到CD等于DM,根据DE等于EM减DM,把EM换为BC加CM的一半,化简后得到值为定值.
【解答】解:(1)如图,过P点作PF∥AC交BC于F,
∵点P和点Q同时出发,且速度相同,
∴BP=CQ,
∵PF∥AQ,
∴∠PFB=∠ACB,∠DPF=∠CQD,
又∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠PFB,
∴BP=PF,
∴PF=CQ,又∠PDF=∠QDC,
∴证得△PFD≌△QCD,
∴DF=CD=12CF,
又因P是AB的中点,PF∥AQ,
∴F是BC的中点,即FC=12BC=3,
∴CD=12CF=32;
(2)分两种情况讨论,得ED为定值,是不变的线段,
如图,如果点P在线段AB上,
过点P作PF∥AC交BC于F,
∵△PBF为等腰三角形,
∴PB=PF,
BE=EF,
∴PF=CQ,
∴FD=DC,
∴ED=EF+FD=BE+DC=12BC=3,
∴ED为定值,
同理,如图,若P在BA的延长线上,
作PM∥AC的延长线于M,
∴∠PMC=∠ACB,
又∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠PMC,
∴PM=PB,根据三线合一得BE=EM,
同理可得△PMD≌△QCD,
所以CD=DM,
∵BE=EM,CD=DM,
∴ED=EM﹣DM=BC+CM2−DM=BC2+CM2−DM=3+DM﹣DM=3,
综上所述,线段ED的长度保持不变.
沪科版(2024)八年级上册14.1 全等三角形达标测试: 这是一份沪科版(2024)八年级上册<a href="/sx/tb_c27310_t7/?tag_id=28" target="_blank">14.1 全等三角形达标测试</a>,共47页。
沪科版(2024)八年级上册14.1 全等三角形同步练习题: 这是一份沪科版(2024)八年级上册<a href="/sx/tb_c27310_t7/?tag_id=28" target="_blank">14.1 全等三角形同步练习题</a>,共31页。
初中第12章 一次函数12.1 函数课时训练: 这是一份初中<a href="/sx/tb_c27302_t7/?tag_id=28" target="_blank">第12章 一次函数12.1 函数课时训练</a>,共35页。













