中考数学解题大招复习讲义(全国通用)模型15十字架模型(原卷版+解析)

这是一份中考数学解题大招复习讲义(全国通用)模型15十字架模型(原卷版+解析)，共46页。试卷主要包含了正方形中的十字模型等内容，欢迎下载使用。

★模型巧记：正方形内十字架模型，垂直一定相等，相等不一定垂直.
★点拨：无论怎么变，只要垂直，十字架就相等.

例题精讲
考点一、正方形中的十字模型
【例1】．如图，正方形ABCD中，点E，F分别在边CD，AD上，BE⊥CF于点G，若BC＝4，AF＝1，则GF的长为_______
变式训练
【变式1-1】．如图，在正方形ABCD中，E为BC边上一点，连接AE，作AE的垂直平分线交AB于G，交CD于F．若DF＝2，BG＝4，则GF的长为 ．
【变式1-2】．如图，在正方形ABCD中，点E，F分别在AD，CD上，且AE＝DF＝2，BE与AF相交于点O，P是BF的中点，连接OP，若AB＝5，则OP的长为 ．
【变式1-3】．如图，在正方形ABCD中，点E是边BC上的一点，点F在边CD的延长线上，且BE＝DF，连接EF交边AD于点G．过点A作AN⊥EF，垂足为点M，交边CD于点N．若BE＝5，CN＝8，则线段AN的长为 ．
考点二：矩形中的十字模型
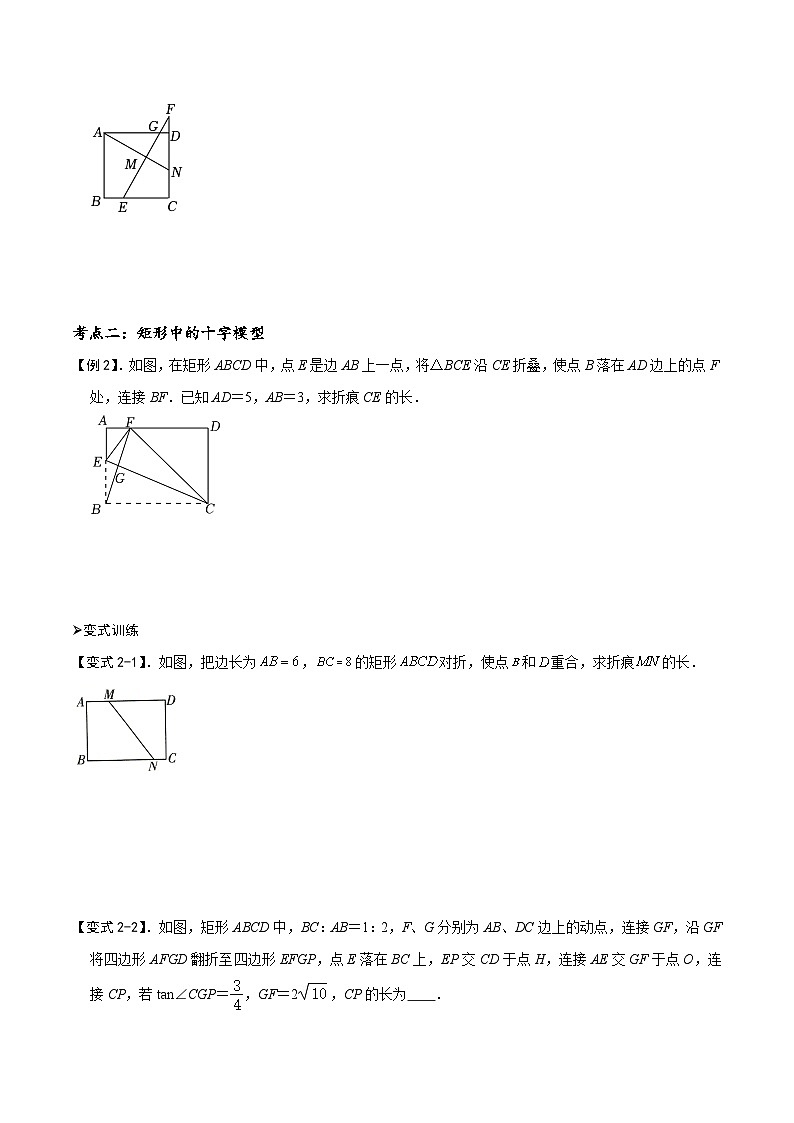
【例2】．如图，在矩形ABCD中，点E是边AB上一点，将△BCE沿CE折叠，使点B落在AD边上的点F处，连接BF．已知AD＝5，AB＝3，求折痕CE的长．
变式训练
【变式2-1】．如图，把边长为，的矩形对折，使点和重合，求折痕的长．
【变式2-2】．如图，矩形ABCD中，BC：AB＝1：2，F、G分别为AB、DC边上的动点，连接GF，沿GF将四边形AFGD翻折至四边形EFGP，点E落在BC上，EP交CD于点H，连接AE交GF于点O，连接CP，若tan∠CGP＝，GF＝2，CP的长为 ．
【变式2-3】．如图，在矩形ABCD中，AB＝5，AD＝10．若点E是边AD上的一个动点，过点E作EF⊥AC且分别交对角线AC、直线BC于点O、F，则在点E移动的过程中，AF+FE+EC的最小值为 ．

实战演练
1．如图，在边长为4的正方形ABCD中，点E、F分别是边BC、CD上的动点，且BE＝CF，连接BF、DE，则BF+DE的最小值为（ ）
A．8B．4C．4D．4
2．如图，在正方形ABCD中，E，F分别是AB，BC的中点，CE，DF交于点G，连接AG．下列结论：①CE＝DF；②CE⊥DF；③∠AGE＝∠CDF．其中正确的结论是（ ）
A．①②B．①③C．②③D．①②③
3．如图，在矩形ABCD中，AB＝10，AD＝6，E为BC上一点，把△CDE沿DE折叠，使点C落在AB边上的F处，则CE的长为 ．
4．如图，在Rt△ACB中，AC＝4，BC＝3，点D为AC中点，连接BD，作CE⊥BD交AB于点E，垂足为F，则CE＝ ．
5．如图，将边长为4的正方形ABCD折叠，使得点A落在CD的中点E处，折痕为FG，点F在AD边上，则FG＝ ．
6．如图，在边长为2的正方形ABCD中，点E，F分别是边AB，BC的中点，连接EC，FD，点G，H分别是EC，FD的中点，连接GH，则GH的长度为 ．
7．如图，正方形ABCD的边长是9，点E是AB边上的一个动点，点F是CD边上一点，CF＝4，连接EF，把正方形ABCD沿EF折叠，使点A，D分别落在点A′，D′处，当点D′落在直线BC上时，线段AE的长为 ．
8．如图，在Rt△ABC中，∠ABC＝90°，BA＝BC，点D为BC边的中点，BE⊥AD于点E，交AC于点F，求的值．
9．如图，在四边形ABCD中，∠ABC＝90°，AB＝AD＝10，BC＝CD＝5，点M，N分别在边BC，AB上，且AM⊥DN，的值．
10．矩形ABCD中，AB＝8，AD＝12．将矩形折叠，使点A落在点P处，折痕为DE．
（1）如图①，若点P恰好在边BC上，连接AP，求的值；
（2）如图②，若E是AB的中点，EP的延长线交BC于点F，求BF的长．
11．已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．
（1）如图①，若四边形ABCD是矩形，且DE⊥CF，求证：△ADE∽△DCF；
（2）如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，成立？并证明你的结论；
（3）如图③，若BA＝BC＝6，DA＝DC＝8，∠BAD＝90°，DE⊥CF，请直接写出的值．
12．在矩形ABCD中，AB＝a，AD＝b，EF⊥GH于M，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H．
（1）【观察猜想】如图①，当a＝b时，线段EF与线段GH的数量关系是 ．
（2）【类比探究】如图②，当a≠b时，（1）中的结论是否仍然成立？若成立，请说明理由，若不成立，请写出正确的结论，并说明理由．
（3）【拓展运用】如图③，在四边形ABCD中，BC＝CD＝5，∠B＝∠ADC＝90°，AE⊥DF于G，点E、F分别在边BC、AB上，若＝，求AB的长．
13．华师版八年级下册数学教材第121页习题19.3第2小题及参考答案．
某数学兴趣小组在完成了以上解答后，决定对该问题进一步探究．
【问题探究】
如图1，在正方形ABCD中，点E、F、G、H分别在线段AB、BC、CD、DA上，且EG⊥FH．试猜想的值，并证明你的猜想．
【知识迁移】
如图2，在矩形ABCD中，AB＝m，BC＝n，点E、F、G、H分别在线段AB、BC、CD、DA上，且EG⊥FH．则＝ ．
【拓展应用】
如图3，在四边形ABCD中，∠DAB＝90°，∠ABC＝60°，AB＝BC，点E、F分别在线段AB、AD上，且CE⊥BF．求的值．

14．（1）证明推断：如图（1），在正方形ABCD中，点E、Q分别在边BC、AB上，DQ⊥AE于点O，点G、F分别在边CD、AB上，GF⊥AE．
①填空：DQ AE（填“＞”“＜”或“＝”）；②推断的值为 ；
（2）类比探究：如图（2），在矩形ABCD中，＝k（k为常数）．将矩形ABCD沿GF折叠，使点A落在BC边上的点E处，得到四边形FEPG，EP交CD于点H，连接AE交GF于点O．试探究GF与AE之间的数量关系，并说明理由；
（3）拓展应用：在（2）的条件下，连接CP，当k＝时，若＝，GF＝2，求CP的长．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/3/2 20:2
6:29；用户15．在四边形ABCD中，对角线AC、BD相交于点O，过点O的直线分别交边AB、CD、AD、BC于点E、F、G、H
【感知】如图①，若四边形ABCD是正方形，且EF⊥GH，易知S△BOE＝S△AOG，又因为S△AOB＝S四边形ABCD，所以S四边形AEOG＝S正方形ABCD（不要求证明）；
【拓展】如图②，若四边形ABCD是矩形，且S四边形AEOG＝S矩形ABCD，若AB＝a，AD＝b，BE＝m，求AG的长（用含a、b、m的代数式表示）；
【探究】如图③，若四边形ABCD是平行四边形，且S四边形AEOG＝S▱ABCD，若AB＝3，AD＝5，BE＝1，则AG＝ ．
如图，在正方形ABCD中，CE⊥DF．求证：CE＝DF．
证明：设CE与DF交于点O，
∵四边形ABCD是正方形，
∴∠B＝∠DCF＝90°，BC＝CD．
∴∠BCE+∠DCE＝90°，
∵CE⊥DF，
∴∠COD＝90°．
∴∠CDF+∠DCE＝90°．
∴∠CDF＝∠BCE，
∴△CBE≌△DFC．
∴CE＝DF．
模型介绍
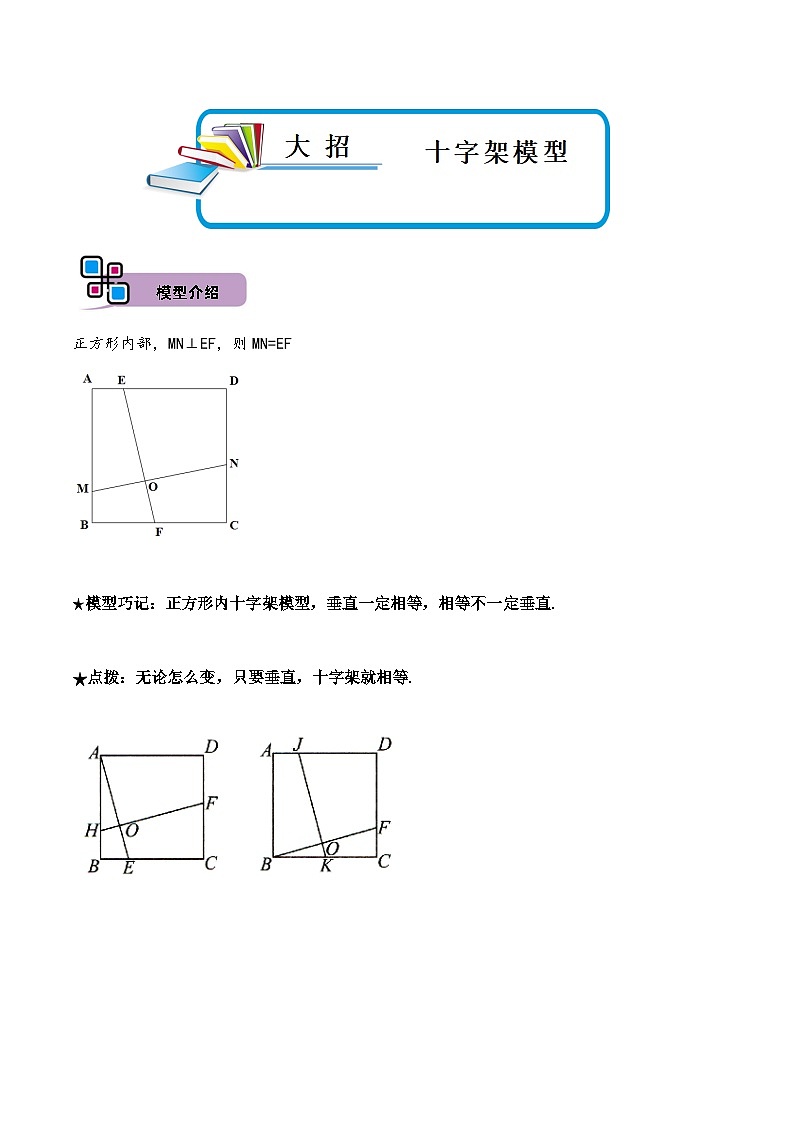
正方形内部，MN⊥EF，则MN=EF
★模型巧记：正方形内十字架模型，垂直一定相等，相等不一定垂直.
★点拨：无论怎么变，只要垂直，十字架就相等.

例题精讲
考点一、正方形中的十字模型
【例1】．如图，正方形ABCD中，点E，F分别在边CD，AD上，BE⊥CF于点G，若BC＝4，AF＝1，则GF的长为_______
解：∵正方形ABCD的边BC＝4，
∴BC＝CD＝AD＝4，∠BCE＝∠CDF＝90°，
∵BE⊥CF于点G，
∴∠CBG+∠BCG＝∠BCG+∠DCF＝90°，
∴∠CBE＝∠DCF，
在△BCE和△CDF中，
，
∴△BCE≌△CDF（ASA），
∴CE＝DF，BE＝CF，
∵DF＝AD﹣AF＝4﹣1＝3，
∴CE＝3，
∴＝5，
∴BE＝5，
∵，
∴CG＝，
∴FG＝CF﹣CG＝．
变式训练
【变式1-1】．如图，在正方形ABCD中，E为BC边上一点，连接AE，作AE的垂直平分线交AB于G，交CD于F．若DF＝2，BG＝4，则GF的长为 3 ．
解：如图，连接GE，作GH⊥CD于H．则四边形AGHD是矩形，设AG＝DH＝x，则FH＝x﹣2．
∵GF垂直平分AE，四边形ABCD是正方形，
∴∠ABE＝∠GHF＝90°，AB＝AD＝GH，AG＝GE＝x，
∵∠BAE+∠AGF＝90°，∠AGF+∠FGH＝90°，
∴∠BAE＝∠FGH，
∴△ABE≌△GHF，
∴BE＝FH＝x﹣2，AE＝GF．
在Rt△BGE中，∵GE2＝BG2+BE2，
∴x2＝42+（x﹣2）2，
∴x＝5，
∴AB＝9，BE＝3，
在Rt△ABE中，AE＝＝＝3．
∴FG＝3．
故答案为：3．
【变式1-2】．如图，在正方形ABCD中，点E，F分别在AD，CD上，且AE＝DF＝2，BE与AF相交于点O，P是BF的中点，连接OP，若AB＝5，则OP的长为 ．
解：∵四边形ABCD为正方形，
∴∠BAE＝∠D＝90°，AB＝AD，
在△ABE和△DAF中，
，
∴△ABE≌△DAF（SAS），
∴∠ABE＝∠DAF，
∵∠ABE+∠BEA＝90°，
∴∠DAF+∠BEA＝90°，
∴∠AOE＝∠BOF＝90°，
∵点P为BF的中点，
∴OP＝BF，
∵BC＝5、CF＝CD﹣DF＝5﹣2＝3，
∴BF＝，
∴GH＝BF＝，
故答案为：．
【变式1-3】．如图，在正方形ABCD中，点E是边BC上的一点，点F在边CD的延长线上，且BE＝DF，连接EF交边AD于点G．过点A作AN⊥EF，垂足为点M，交边CD于点N．若BE＝5，CN＝8，则线段AN的长为 4 ．
解：如图，连接AE，AF，EN，
∵四边形ABCD为正方形，
∴AB＝AD，BC＝CD，∠ABE＝∠BCD＝∠ADF＝90°，
在△ABE和△ADF中，
，
∴△ABE≌△ADF（SAS），
∴∠BAE＝∠DAF，AE＝AF，
∴∠EAF＝90°，
∴△EAF为等腰直角三角形，
∵AN⊥EF，
∴EM＝FM，∠EAM＝∠FAM＝45°，
∴△AEM≌△AFM（SAS），△EMN≌△FMN（SAS），
∴EN＝FN，
设DN＝x，
∵BE＝DF＝5，CN＝8，
∴CD＝CN+DN＝x+8，
∴EN＝FN＝DN+DF＝x+5，CE＝BC﹣BE＝CD﹣BE＝x+8﹣5＝x+3，
在Rt△ECN中，由勾股定理可得：
CN2+CE2＝EN2，
即82+（x+3）2＝（x+5）2，
解得：x＝12，
∴DN＝12，AD＝BC＝BE+CE＝5+x+3＝20，
∴AN＝＝＝4，
故答案为：4．
考点二：矩形中的十字模型
【例2】．如图，在矩形ABCD中，点E是边AB上一点，将△BCE沿CE折叠，使点B落在AD边上的点F处，连接BF．已知AD＝5，AB＝3，求折痕CE的长．
解：由翻折的性质可知，BE＝EF，BC＝FC＝AD＝5，
在Rt△CDF中，CF＝5，CD＝AB＝3，
∴DF＝＝4，
∴AF＝AD﹣DF＝5﹣4＝1，
设BE＝x，则EF＝x，AE＝3﹣x，
在Rt△AEF中，由勾股定理得，
AF2+AE2＝EF2，
即1+（3﹣x）2＝x2，
解得x＝，
即BE＝，
在Rt△BCE中，由勾股定理得，
CE＝
＝
＝， 故答案为：．
变式训练
【变式2-1】．如图，把边长为，的矩形对折，使点和重合，求折痕的长．
解：如图，过点作，垂足为，连接，
在中，，，∴，
由折叠得，，∴，
∵，∴，
∵，∴，∴，∴，∴
【变式2-2】．如图，矩形ABCD中，BC：AB＝1：2，F、G分别为AB、DC边上的动点，连接GF，沿GF将四边形AFGD翻折至四边形EFGP，点E落在BC上，EP交CD于点H，连接AE交GF于点O，连接CP，若tan∠CGP＝，GF＝2，CP的长为 ．
解：过点P作PK⊥BC，交BC的延长线于点K，如图所示：
由折叠的性质得：∠FEP＝∠FAD＝∠D＝∠EPG＝90°，
∴∠CGP+∠GHP＝90°，
∵∠PEC+∠EHC＝90°，∠GHP＝∠EHC，
∴∠PEC＝∠CGP，
∵∠BEF+∠BFE＝∠BEF+∠PEC＝90°，
∴∠BFE＝∠PEC＝∠CGP，
∵tan∠CGP＝，
∴tan∠BFE＝＝，
设BE＝3x，则BF＝4x，
∴AF＝EF＝＝＝5x，
∴AB＝AF+BF＝5x+4x＝9x，
由折叠的性质得：∠AOF＝∠EOF，
∴∠AOF＝∠EOF＝90°，
过G作GM⊥AB于M，
则∠FMG＝90°，四边形ADGM是矩形，
∴AD＝GM，∠MFG+∠MGF＝90°，
∵∠AOF＝90°，
∴∠MFG+∠FAO＝90°，
∴∠BAE＝∠MGF，
∵四边形ABCD是矩形，
∴AD＝BC，∠BAD＝∠D＝∠B＝90°＝∠FMG，
∴△ABE∽△GMF，
∴＝＝＝＝2，
∴AE＝2GF＝2×2＝4，
在Rt△ABE中，由勾股定理得：AB2+BE2＝AE2，
即：81x2+9x2＝160，
解得：x＝或x＝﹣（舍去），
∴AB＝9×＝12，BE＝3×＝4，
∴EP＝AD＝AB＝6，CE＝BC﹣BE＝6﹣4＝2，
∴tan∠PEK＝＝tan∠CGP＝，
设PK＝3y，则EK＝4y，
在Rt△PEK中，由勾股定理得 EK2+PK2＝EP2，
即：16x2+9y2＝36，
解得：y＝或y＝﹣（舍去），
∴PK＝3×＝，EK＝4×＝，
∴CK＝EK﹣CE＝﹣2＝，
∴CP＝＝＝， 故答案为：．
【变式2-3】．如图，在矩形ABCD中，AB＝5，AD＝10．若点E是边AD上的一个动点，过点E作EF⊥AC且分别交对角线AC、直线BC于点O、F，则在点E移动的过程中，AF+FE+EC的最小值为 + ．
解：如图，过点E作EH⊥BC于点H．
∵四边形ABCD是矩形，
∴∠B＝∠BAD＝∠BHE＝90°，
∴四边形ABHE是矩形，
∴EH＝AB＝5，
∵BC＝AD＝10，
∴AC＝＝＝5，
∵EF⊥AC，
∴∠COF＝90°，
∴∠EFH+∠ACB＝90°，
∵∠BAC+∠ACB＝90°，
∴∠EFH＝∠BAC，
∴△EHF∽△CBA，
∴＝＝，
∴＝＝，
∴FH＝，EF＝，
设BF＝x，则DE＝10﹣x﹣＝﹣x，
∵EF是定值，
∴AF+CE的值最小时，AF+EF+CE的值最小，
∵AF+CE＝+，
∴欲求AF+CE的最小值相当于在x轴上找一点P（x，0），使得P到A（0，5），B（，5）的距离和最小，如图1中，
作点A关于x轴的对称点A′，连接BA′交xz轴于点P，连接AP，此时PA+PB的值最小，最小值为线段A′B的长，
∵A′（0，﹣5），B（，5），
∴A′B＝＝，
∴AF+CE的最小值为，
∴AF+EF+CE的最小值为+．
解法二：过点C作CC′∥EF，使得CC′＝EF，连接C′F．
∵EF＝CC′，EF∥CC′，
∴四边形EFC′C是平行四边形，
∴EC＝FC′，
∵EF⊥AC，
∴AC⊥CC′，
∴∠ACC＝90°，
∵AC′＝＝＝，
∴AF+EC＝AF+FC′≥AC′＝，
∴AF+EF+CE的最小值为+．
故答案为：+．

实战演练
1．如图，在边长为4的正方形ABCD中，点E、F分别是边BC、CD上的动点，且BE＝CF，连接BF、DE，则BF+DE的最小值为（ ）
A．8B．4C．4D．4
解：连接AE，如图1，
∵四边形ABCD是正方形，
∴AB＝BC，∠ABE＝∠BCF＝90°．
又BE＝CF，
∴△ABE≌△BCF（SAS）．
∴AE＝BF．
所以BF+DE最小值等于AE+DE最小值．
作点A关于BC的对称点H点，如图2，
连接BH，则A、B、H三点共线，
连接DH，DH与BC的交点即为所求的E点．
根据对称性可知AE＝HE，
所以AE+DE＝DH．
在Rt△ADH中，DH＝＝＝4，
∴BF+DE最小值为4．
故选：D．
2．如图，在正方形ABCD中，E，F分别是AB，BC的中点，CE，DF交于点G，连接AG．下列结论：①CE＝DF；②CE⊥DF；③∠AGE＝∠CDF．其中正确的结论是（ ）
A．①②B．①③C．②③D．①②③
解：∵四边形ABCD是正方形，
∴AB＝BC＝CD＝AD，∠B＝∠BCD＝90°，
∵E，F分别是AB，BC的中点，
∴BE＝AB，CF＝BC，
∴BE＝CF，
在△CBE与△DCF中，
，
∴△CBE≌△DCF（SAS），
∴∠ECB＝∠CDF，CE＝DF，故①正确；
∵∠BCE+∠ECD＝90°，
∴∠ECD+∠CDF＝90°，
∴∠CGD＝90°，
∴CE⊥DF，故②正确；
∴∠EGD＝90°，
延长CE交DA的延长线于H，
∵点E是AB的中点，
∴AE＝BE，
∵∠AHE＝∠BCE，∠AEH＝∠CEB，AE＝BE，
∴△AEH≌△BEC（AAS），
∴BC＝AH＝AD，
∵AG是斜边的中线，
∴AG＝DH＝AD，
∴∠ADG＝∠AGD，
∵∠AGE+∠AGD＝90°，∠CDF+∠ADG＝90°，
∴∠AGE＝∠CDF．故③正确；
故选：D．
3．如图，在矩形ABCD中，AB＝10，AD＝6，E为BC上一点，把△CDE沿DE折叠，使点C落在AB边上的F处，则CE的长为 ．
解：设CE＝x，则BE＝6﹣x由折叠性质可知，EF＝CE＝x，DF＝CD＝AB＝10，
在Rt△DAF中，AD＝6，DF＝10，
∴AF＝8，
∴BF＝AB﹣AF＝10﹣8＝2，
在Rt△BEF中，BE2+BF2＝EF2，
即（6﹣x）2+22＝x2，
解得x＝，
故答案为．
4．如图，在Rt△ACB中，AC＝4，BC＝3，点D为AC中点，连接BD，作CE⊥BD交AB于点E，垂足为F，则CE＝ ．
解：如图，过点A、B分别作AC、BC的垂线，两垂线相交于点G，延长CE交AG于点H，
∵△ACB是直角三角形，
∴四边形ACBG为矩形，
∵点D为AC中点，AC＝4，
∴CD＝AD＝2，
∵BC＝3，
∴BD＝＝＝，
∵CE⊥BD，
∴∠CDB+∠DCH＝90°，∠CDB+∠DBC＝90°，
∴∠DCH＝∠DBC，
∴Rt△AHC∽Rt△CDB，
∴＝＝，即＝＝，
∴CH＝，AH＝；
在矩形ACBG中，AH∥CB，
∴△AEH∽△BEC，
∴＝＝，即＝，
解得：CE＝．
故答案为：．
5．如图，将边长为4的正方形ABCD折叠，使得点A落在CD的中点E处，折痕为FG，点F在AD边上，则FG＝ 2 ．
解：如图，连接AE，过点G作GM⊥AD于M，则四边形ABGM中，MG＝AB，
由翻折变换的性质得GF⊥AE，
∵∠AFG+∠DAE＝90°，∠AED+∠DAE＝90°，
∴∠AFG＝∠AED，
∵四边形ABCD是正方形，
∴AD＝AB，
∴MG＝AD，
∴△ADE≌△GMF（AAS），
∴GF＝AE，
∵点E是CD的中点，
∴DE＝CD＝2，
在Rt△ADE中，由勾股定理得，AE＝＝＝2，
∴GF的长为2．
故答案为：2．
6．如图，在边长为2的正方形ABCD中，点E，F分别是边AB，BC的中点，连接EC，FD，点G，H分别是EC，FD的中点，连接GH，则GH的长度为 1 ．
解：方法一：连接CH并延长交AD于P，连接PE，
∵四边形ABCD是正方形，
∴∠A＝90°，AD∥BC，AB＝AD＝BC＝2，
∵E，F分别是边AB，BC的中点，
∴AE＝CF＝×2＝，
∵AD∥BC，
∴∠DPH＝∠FCH，
∵∠DHP＝∠FHC，
∵DH＝FH，
∴△PDH≌△CFH（AAS），
∴PD＝CF＝，
∴AP＝AD﹣PD＝，
∴PE＝＝＝2，
∵点G，H分别是EC，CP的中点，
∴GH＝EP＝1；
方法二：设DF，CE交于O，
∵四边形ABCD是正方形，
∴∠B＝∠DCF＝90°，BC＝CD＝AB，
∵点E，F分别是边AB，BC的中点，
∴BE＝CF，
∴△CBE≌△DCF（SAS），
∴CE＝DF，∠BCE＝∠CDF，
∵∠CDF+∠CFD＝90°，
∴∠BCE+∠CFD＝90°，
∴∠COF＝90°，
∴DF⊥CE，
∴CE＝DF＝＝，
∵点G，H分别是EC，PC的中点，
∴CG＝FH＝，
∵∠DCF＝90°，CO⊥DF，
∴∠DCO+∠FCO＝∠DCO+∠CDO＝90°，
∴∠FCO＝∠CDO，
∵∠DCF＝∠COF＝90°，
∴△COF∽△DOC，
∴＝，
∴CF2＝OF•DF，
∴OF＝＝＝，
∴OH＝，OD＝，
∵∠COF＝∠COD＝90°，
∴△COF∽△DCF，
∴，
∴OC2＝OF•OD，
∴OC＝＝，
∴OG＝CG﹣OC＝﹣＝，
∴HG＝＝＝1，
故答案为：1．
7．如图，正方形ABCD的边长是9，点E是AB边上的一个动点，点F是CD边上一点，CF＝4，连接EF，把正方形ABCD沿EF折叠，使点A，D分别落在点A′，D′处，当点D′落在直线BC上时，线段AE的长为 2或8 ．
解：分两种情况：①当D′落在线段BC上时，连接ED、ED′、DD′，如图1所示：
由折叠可得，D，D'关于EF对称，即EF垂直平分DD'，
∴DE＝D′E，
∵正方形ABCD的边长是9，
∴AB＝BC＝CD＝AD＝9，
∵CF＝4，
∴DF＝D′F＝CD﹣CF＝9﹣4＝5，
∴CD′＝＝3，
∴BD'＝BC﹣CD'＝6，
设AE＝x，则BE＝9﹣x，
在Rt△AED和Rt△BED'中，由勾股定理得：DE2＝AD2+AE2＝92+x2，D'E2＝BE2+BD'2＝（9﹣x）2+62，
∴92+x2＝（9﹣x）2+62，
解得：x＝2，
即AE＝2；
②当D′落在线段BC延长线上时，连接ED、ED′、DD′，如图2所示：
由折叠可得，D，D'关于EF对称，即EF垂直平分DD'，
∴DE＝D′E，
∵正方形ABCD的边长是9，
∴AB＝BC＝CD＝AD＝9，
∵CF＝4，
∴DF＝D′F＝CD﹣CF＝9﹣4＝5，CD′＝＝3，
∴BD'＝BC+CD'＝12，
设AE＝x，则BE＝9﹣x，
在Rt△AED和Rt△BED'中，由勾股定理得：DE2＝AD2+AE2＝92+x2，D'E2＝BE2+BD'2＝（9﹣x）2+122，
∴92+x2＝（9﹣x）2+122，
解得：x＝8，即AE＝8；
综上所述，线段AE的长为2或8；
故答案为：2或8．

8．如图，在Rt△ABC中，∠ABC＝90°，BA＝BC，点D为BC边的中点，BE⊥AD于点E，交AC于点F，求的值．
解：如图，过点C作CG⊥AD，交AD的延长线于点G；
∵BE⊥AD，
∴BE∥CG，△BDE∽△CDG，
∴，
∵BD＝CD，
∴DE＝DG；
设AB＝2λ，则BD＝λ；
∵∠ABD＝90°，BE⊥AD，
∴AD＝，AB2＝AE•AD，
∴AE＝，DE＝AD﹣AE＝λ，
∴GE＝2DE＝；
∵EF∥CG，
∴＝．
9．如图，在四边形ABCD中，∠ABC＝90°，AB＝AD＝10，BC＝CD＝5，点M，N分别在边BC，AB上，且AM⊥DN，的值．
解：过点D作AB的平行线，交过点A作BC的平行线于G，交BC的延长线于H，过点D作DP⊥AB于P，
则四边形ABHG是矩形，
∵AB＝AD，CB＝CD，
∴∠ADC＝∠ABC＝90°，
∴∠ADG+∠CDH＝90°，
∵∠ADG+∠DAG＝90°，
∴∠DAG＝∠HDC，
又∵∠G＝∠H，
∴△ADG∽△DCH，
∴，
∴设CH＝x，则DG＝2x，
∴DH＝10﹣2x，AG＝5+x，
∴5+x＝2（10﹣2x），
解得x＝3，
∴BH＝8，
∵∠NDP＝∠BAM，∠DPN＝∠ABM，
∴△ABM∽△DPN，
∴．
10．矩形ABCD中，AB＝8，AD＝12．将矩形折叠，使点A落在点P处，折痕为DE．
（1）如图①，若点P恰好在边BC上，连接AP，求的值；
（2）如图②，若E是AB的中点，EP的延长线交BC于点F，求BF的长．
解：（1）如图①中，取DE的中点M，连接PM．
∵四边形ABCD是矩形，
∴∠BAD＝∠C＝90°，
由翻折可知，AO＝OP，AP⊥DE，∠2＝∠3，∠DAE＝∠DPE＝90°，
在Rt△EPD中，∵EM＝MD，
∴PM＝EM＝DM，
∴∠3＝∠MPD，
∴∠1＝∠3+∠MPD＝2∠3，
∵∠ADP＝2∠3，
∴∠1＝∠ADP，
∵AD∥BC，
∴∠ADP＝∠DPC，
∴∠1＝∠DPC，
∵∠MOP＝∠C＝90°，
∴△POM∽△DCP，
∴＝＝＝，
∴＝＝．
解法二：证明△ABP和△DAE相似，＝＝．
（2）如图②中，过点P作GH∥BC交AB于G，交CD于H．则四边形AGHD是矩形，设EG＝x，则BG＝4﹣x
∵∠A＝∠EPD＝90°，∠EGP＝∠DHP＝90°，
∴∠EPG+∠DPH＝90°，∠DPH+∠PDH＝90°，
∴∠EPG＝∠PDH，
∴△EGP∽△PHD，
∴＝＝＝＝，
∴PH＝3EG＝3x，DH＝AG＝4+x，
在Rt△PHD中，∵PH2+DH2＝PD2，
∴（3x）2+（4+x）2＝122，
解得x＝（负值已经舍弃），
∴BG＝4﹣＝，
在Rt△EGP中，GP＝＝，
∵GH∥BC，
∴△EGP∽△EBF，
∴＝，
∴＝，
∴BF＝3．
11．已知四边形ABCD中，E、F分别是AB、AD边上的点，DE与CF交于点G．
（1）如图①，若四边形ABCD是矩形，且DE⊥CF，求证：△ADE∽△DCF；
（2）如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，成立？并证明你的结论；
（3）如图③，若BA＝BC＝6，DA＝DC＝8，∠BAD＝90°，DE⊥CF，请直接写出的值．
（1）证明：∵四边形ABCD是矩形，
∴∠A＝∠ADC＝90°，
∴∠ADE+∠CDG＝90°，
又∵DE⊥CF，∠CDG+∠DCF＝90°，
∴∠ADE＝∠DCF，
∴△ADE∽△DCF．
（2）解：当∠B+∠EGC＝180°时，成立，理由如下：
在AD的延长线上取点M，使CM＝CF，如图1所示：
则∠CMF＝∠CFM．∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥BC，
∴∠A＝∠CDM，∠FCB＝∠CFM，
∵∠B+∠EGC＝180°，
∴∠BEG+∠FCB＝360°﹣（∠B+∠EGC）＝180°，
又∵∠BEG+∠AED＝180°，
∴∠AED＝∠FCB，
∴∠CMF＝∠AED．
∴△ADE∽△DCM，
∴，
∴；
（3）解：；理由如下：
连接AC、BD，交于点M，作CN⊥AD于N，如图2所示：
∵∠BAD＝90°，AB＝6，AD＝8，
∴BD＝＝＝10，
在△ABD和△CBD中，
，
∴△ABD≌△CBD（SSS），
∴∠ABD＝∠CBD，
∵AB＝CB，
∴BD⊥AC，AM＝CM，
∴∠AMD＝90°＝∠BAD，
又∵∠ADB＝∠MDA，
∴△ABD∽△MAD，
∴AD：DM＝BD：AD，
∴AD2＝BD•DM，即82＝10DM，
∴DM＝6.4，
∴AM＝＝＝4.8，
∴AC＝2AM＝9.6，
∵△ACD的面积＝AD•CN＝AC•DM，
∴8×CN＝9.6×6.4，
解得：CN＝7.68，
∵DE⊥CF，
∴∠FCN＝∠EDA，
∵CN⊥AD，
∴∠CNF＝∠DAE，
∴△ADE∽△NCF，
∴＝＝．

12．在矩形ABCD中，AB＝a，AD＝b，EF⊥GH于M，EF分别交AB，CD于点E，F，GH分别交AD，BC于点G，H．
（1）【观察猜想】如图①，当a＝b时，线段EF与线段GH的数量关系是 相等 ．
（2）【类比探究】如图②，当a≠b时，（1）中的结论是否仍然成立？若成立，请说明理由，若不成立，请写出正确的结论，并说明理由．
（3）【拓展运用】如图③，在四边形ABCD中，BC＝CD＝5，∠B＝∠ADC＝90°，AE⊥DF于G，点E、F分别在边BC、AB上，若＝，求AB的长．
解：（1）分别过点G、F作GQ⊥BC于Q，GQ交EF于点N，FP⊥AB于点P，
∵EF⊥GH，
∴∠GMN＝90°，
∴∠QGH+∠GNM＝90°，∠GNM+∠PFE＝90°，
∴∠QGH＝∠PFE，
在△PFE和△QGH中，
，
∴△PFE≌△QGH（ASA），
∴EF＝GH；
（2）不成立，正确的结论为：，理由如下：
分别过点G、F作GQ⊥BC于Q，GQ交EF于点N，FP⊥AB于点P，
∵EF⊥GH，
∴∠GMN＝90°，
∴∠QGH+∠GNM＝90°，∠GNM+∠PFE＝90°，
∴∠QGH＝∠PFE，
∴△PFE∽△QGH，
∴，
∵∠A＝∠B＝∠BQG＝90°，
∴四边形ABQG是矩形，
∴GQ＝a，
同理：FP＝b，
∴，
（3）过点D作DM∥AB，延长BC交MD延长线于N点，过点A作AM⊥DM于M，连接AC，
∵BC＝CD，∠B＝∠ADC＝90°，
∴△RtABC≌Rt△ADC（HL），∴AB＝AD，
∵＝，
由（2）知：，
设AD＝AB＝5a，AM＝4a，由勾股定理得MD＝3a，
∵∠ADC＝90°，
∴∠ADM+∠CDN＝90°，
∵∠ADM+∠DAM＝90°，
∴∠CDN＝∠DAM，
∴△AMD∽△DNC，
∴，
∴， ∴DN＝4，
∴MN＝MD+DN＝3a+4＝5a， ∴a＝2， ∴AB＝5a＝10．
13．华师版八年级下册数学教材第121页习题19.3第2小题及参考答案．
某数学兴趣小组在完成了以上解答后，决定对该问题进一步探究．
【问题探究】
如图1，在正方形ABCD中，点E、F、G、H分别在线段AB、BC、CD、DA上，且EG⊥FH．试猜想的值，并证明你的猜想．
【知识迁移】
如图2，在矩形ABCD中，AB＝m，BC＝n，点E、F、G、H分别在线段AB、BC、CD、DA上，且EG⊥FH．则＝ ．
【拓展应用】
如图3，在四边形ABCD中，∠DAB＝90°，∠ABC＝60°，AB＝BC，点E、F分别在线段AB、AD上，且CE⊥BF．求的值．
解：（1）结论：＝1．
理由：如图（1）中，过点A作AM∥HF交BC于点M，作AN∥EG交CD的延长线于点N，
∴AM＝HF，AN＝EG，
在正方形ABCD中，AB＝AD，∠ABM＝∠BAD＝∠ADN＝90°，
∵EG⊥FH，
∴∠NAM＝90°，
∴∠BAM＝∠DAN，
在△ABM和△ADN中，∠BAM＝∠DAN，AB＝AD，∠ABM＝∠ADN，
∴△ABM≌△ADN（ASA），
∴AM＝AN，即EG＝FH，
∴＝1；
（2）如图（2）中，过点A作AM∥HF交BC于点M，作AN∥EG交CD的延长线于点N，
∴AM＝HF，AN＝EG，
在长方形ABCD中，BC＝AD，∠ABM＝∠BAD＝∠ADN＝90°，
∵EG⊥FH，
∴∠NAM＝90°，
∴∠BAM＝∠DAN．
∴△ABM∽△ADN．
∴＝，
∵AB＝m，BC＝AD＝n，
∴＝．
故答案为：；
（3）如图3中，过点C作CM⊥AB于点M．设CE交BF于点O．
∵CM⊥AB，
∴∠CME＝90°，
∴∠1+∠2＝90°，
∵CE⊥BF，
∴∠BOE＝90°，
∴∠2+∠3＝90°，
∴∠1＝∠3，
∴△CME∽△BAF，
∴＝，
∵AB＝BC，∠ABC＝60°，
∴＝＝sin60°＝．
14．（1）证明推断：如图（1），在正方形ABCD中，点E、Q分别在边BC、AB上，DQ⊥AE于点O，点G、F分别在边CD、AB上，GF⊥AE．
①填空：DQ ＝ AE（填“＞”“＜”或“＝”）；②推断的值为 1 ；
（2）类比探究：如图（2），在矩形ABCD中，＝k（k为常数）．将矩形ABCD沿GF折叠，使点A落在BC边上的点E处，得到四边形FEPG，EP交CD于点H，连接AE交GF于点O．试探究GF与AE之间的数量关系，并说明理由；
（3）拓展应用：在（2）的条件下，连接CP，当k＝时，若＝，GF＝2，求CP的长．
（1）①解：∵四边形ABCD是正方形，
∴AB＝DA，∠ABE＝90°＝∠DAQ．
∴∠QAO+∠OAD＝90°．
∵AE⊥DQ，
∴∠ADO+∠OAD＝90°．
∴∠QAO＝∠ADO．
∴△ABE≌△DAQ（ASA），
∴AE＝DQ．
故答案是：＝；
②解：∵DQ⊥AE，FG⊥AE，
∴DQ∥FG，
∵FQ∥DG，
∴四边形DQFG是平行四边形，
∴FG＝DQ，
∵AE＝DQ，
∴FG＝AE，
∴＝1． 故答案为：1．
（2）解：结论：＝k．
理由：如图2中，作GM⊥AB于M．
∵AE⊥GF，
∴∠AOF＝∠GMF＝∠ABE＝90°，
∴∠BAE+∠AFO＝90°，∠AFO+∠FGM＝90°，
∴∠BAE＝∠FGM，
∴△ABE∽△GMF，
∴＝，
∵∠AMG＝∠D＝∠DAM＝90°，
∴四边形AMGD是矩形，
∴GM＝AD，
∴＝＝＝k．
（3）解：如图2中，作PN⊥BC交BC的延长线于N．
由＝，可以假设BE＝3k，BF＝4k，EF＝AF＝5k，
∵＝，FG＝2，
∴AE＝3，
∴（3k）2+（9k）2＝（3）2，
∴k＝1或﹣1（舍弃），
∴BE＝3，AB＝9，
∵BC：AB＝2：3，
∴BC＝6，
∴BE＝CE＝3，AD＝PE＝BC＝6，
∵∠EBF＝∠FEP＝∠PME＝90°，
∴∠FEB+∠PEN＝90°，∠PEN+∠EPN＝90°，
∴∠FEB＝∠EPN，
∴△FBE∽△ENP，
∴＝＝，
∴＝＝，
∴EN＝，PN＝，
∴CN＝EN﹣EC＝﹣3＝，
∴PC＝＝．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/3/2 20:26:29；用户：初中数学；邮箱：lsjycs@xyh.cm；学号：30145887
15．在四边形ABCD中，对角线AC、BD相交于点O，过点O的直线分别交边AB、CD、AD、BC于点E、F、G、H
【感知】如图①，若四边形ABCD是正方形，且EF⊥GH，易知S△BOE＝S△AOG，又因为S△AOB＝S四边形ABCD，所以S四边形AEOG＝S正方形ABCD（不要求证明）；
【拓展】如图②，若四边形ABCD是矩形，且S四边形AEOG＝S矩形ABCD，若AB＝a，AD＝b，BE＝m，求AG的长（用含a、b、m的代数式表示）；
【探究】如图③，若四边形ABCD是平行四边形，且S四边形AEOG＝S▱ABCD，若AB＝3，AD＝5，BE＝1，则AG＝ ．
解：【拓展】
如图②，过O作OM⊥AB于M，ON⊥AD于N，（1分）
∵S△AOB＝S矩形ABCD，（2分）
S四边形AEOG＝，
∴S△AOB＝S四边形AEOG，（3分）
∵S△BOE＝＝＝mb，（4分）
S△AOG＝AG•ON＝AG＝AG•a，（5分）
∴mb＝AG•a，（6分）
∴AG＝；（7分）
【探究】
如图③，过O作QM⊥AB，PN⊥AD，
则MQ＝2OM，PN＝2ON，
∵S▱ABCD＝AB•MQ＝AD•PN，
∴3×2OM＝5×2ON，
∴＝，
∵S△AOB＝S▱ABCD，
S四边形AEOG＝S▱ABCD，
∴S△AOB＝S四边形AEOG，
∵S△BOE＝＝×1×OM，
S△AOG＝AG•ON，
∴×1×OM＝AG•ON，
OM＝AG•ON，
＝AG＝，
∴AG＝；（9分）
故答案为：．

如图，在正方形ABCD中，CE⊥DF．求证：CE＝DF．
证明：设CE与DF交于点O，
∵四边形ABCD是正方形，
∴∠B＝∠DCF＝90°，BC＝CD．
∴∠BCE+∠DCE＝90°，
∵CE⊥DF，
∴∠COD＝90°．
∴∠CDF+∠DCE＝90°．
∴∠CDF＝∠BCE，
∴△CBE≌△DFC．
∴CE＝DF．