





数学七年级上册(2024)3 探索与表达规律教案配套课件ppt
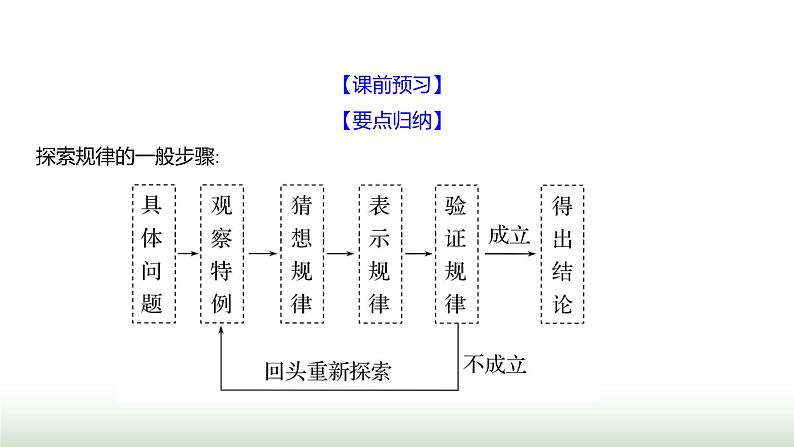
展开【课前预习】【要点归纳】探索规律的一般步骤:
【对点小练】观察下列等式:4×12-12=3,4×22-32=7,4×32-52=11,…,根据上述规律,则第2 020个等式的值是( )A.8 079 B.8 073 C.8 075 D.8 076
【变式训练】(2024·滁州期中)观察下列关于x的单项式,探究其规律:-2x,4x2,-6x3,8x4,-10x5,12x6,…,按照上述规律,第2 023个单项式是( )A.-4 046x2 022B.4 046x2 022C.-4 046x2 023D.4 046x2 023【解析】根据所给单项式发现第奇数个单项式的系数为负,第偶数个单项式的系数为正,第n个单项式系数的绝对值是2n,指数是n,即公式为2n·(-x)n,所以第2 023个单项式是-4 046x2 023.
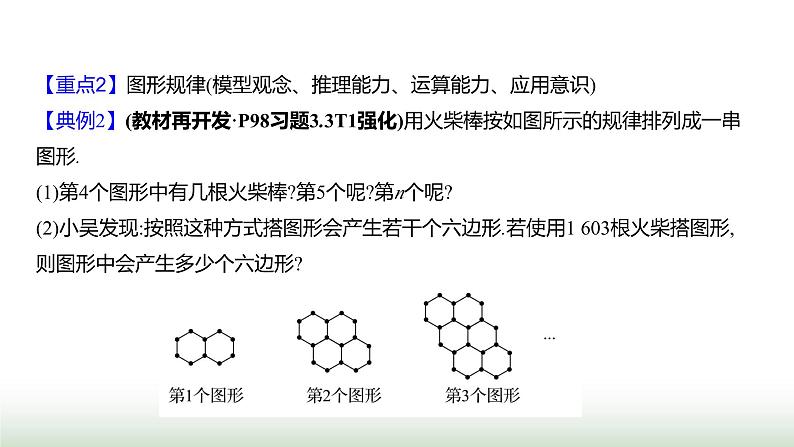
【重点2】图形规律(模型观念、推理能力、运算能力、应用意识)【典例2】(教材再开发·P98习题3.3T1强化)用火柴棒按如图所示的规律排列成一串图形.(1)第4个图形中有几根火柴棒?第5个呢?第n个呢?(2)小吴发现:按照这种方式搭图形会产生若干个六边形.若使用1 603根火柴搭图形,则图形中会产生多少个六边形?
【自主解答】(1)第1个图形:11=8×1+3;第2个图形:19=8×2+3;第3个图形:27=8×3+3;第4个图形:35=8×4+3;第5个图形:43=8×5+3;第n个图形:8×n+3=8n+3.答:第4个图形中有35根火柴棒,第5个有43根火柴棒,第n个有(8n+3)根火柴棒.
(2)依题意,得8n+3=1 603,解得n=200,因为第1个图形中有2个六边形;第2个图形中有4个六边形;第3个图形中有6个六边形……所以第n个图形中有2n个六边形,所以2n=400,即图形中会产生400个六边形.
【变式训练】(2024·北京期末)观察下列图形,则第n个图形中三角形的个数为( )A.2n+1B.4n+4C.4n-4D.4n【解析】第1个图形有1×4=4个三角形,第2个图形有2×4=8个三角形,第3个图形有3×4=12个三角形,…所以第n个图形有4n个三角形.
【课堂小测(8分钟)】1.按一定规律排列的单项式:-x2,x4,-x6,x8,-x10,…,第n个单项式是( )A.(-1)nx2nB.(-1)n-1x2nC.(-1)n+1x2nD.(-1)nxn【解析】因为-x2,x4,-x6,x8,-x10,…,所以第n个单项式为:(-1)nx2n.
2.如图所示是用棋子摆成的“上”字图案,按照这种规律继续摆下去,通过观察、对比、总结,找出规律,解答下列问题.(1)摆成第1个图形需要________枚棋子,摆成第2个图形需要________枚棋子,摆成第3个图形需要________枚棋子; (2)摆成第n个图形需要________枚棋子(用含n的代数式表示); (3)七(1)班有50名学生,把每名学生当成一枚“棋子”,能否让这50枚“棋子”按照以上规律恰好站成一个“上”字?若能,请问能站成第几个图形?并计算最下面一“横”的学生数;若不能,请说明理由.
【解析】(1)由题图可知:摆成第1个图形需要6枚棋子,摆成第2个图形需要10枚棋子,摆成第3个图形需要14枚棋子;答案:6 10 14(2)由题图可知,后一个图形比前一个图形多4枚棋子,所以摆成第n个图形需要6+4(n-1)=4n+2(枚)棋子;答案:(4n+2)(3)能.当4n+2=50时,n=12,所以能站成,能站成第12个图形.由题图可知,最下面一“横”上的棋子的个数是从3开始的连续的奇数,所以3+2×(12-1)=25,即最下面一“横”的学生数是25.
【课后提升】【基础练】1.(2024·河源和平期末)用木棒按如图所示的规律摆放图形,第100个图形需要的木棒根数是( ) A.501B.502C.503D.504
【解析】因为第1个图形需要的木棒根数为6,第2个图形需要的木棒根数为11=6+5=6+5×1,第3个图形需要的木棒根数为16=6+5+5=6+5×2,…,所以第n个图形需要的木棒根数为6+5(n-1)=5n+1,所以第100个图形需要的木棒根数为5×100+1=501.
2.(2024·揭阳揭西期末)如图所示的运算程序中,若开始输入的x值为36,我们发现第1次输出的结果为18,第2次输出的结果为9……第2 022次输出的结果为____.
【能力练】3.如图所示的图形都是由大小相同的小正方形按一定的规律组成的,且每个小正方形的边长都是1,则第7个图形的周长是_______.
【解析】观察题中图形的变化可知:第1个图形的周长是6,第2个图形的周长是12=6+6=6×2,第3个图形的周长是18=6+6+6=6×3…,所以第n个图形的周长是6n,所以第7个图形的周长是6×7=42.
4.(2024·东莞期末)将正整数按如图所示的位置顺序排列,我们称每一个阶段的最高点为“峰”,最低点为“谷”.例如,数字3的位置称为“峰1”,数字6的位置称为“谷1”,数字9的位置称为“峰2”,则“峰7”位置的数字为_______. 【解析】由题干所给图形可知,“峰1”位置的数为3=1×6-3;“峰2”位置的数为9=2×6-3;“峰3”位置的数为15=3×6-3;…,所以“峰i”位置的数为(6i-3)(i为正整数),当i=7时,6i-3=6×7-3=39,即“峰7”位置的数为39.
【培优练】5.(推理能力、几何直观、运算能力)(2024·珠海斗门期末)综合与实践:观察下图,解答下列问题.(1)第1个图形中的一些圆圈被直线分层隔开,第1层有1个圆圈,第2层有3个圆圈,第3层有5个圆圈……如果要你继续画下去,第6层有________个圆圈,第n层有________个圆圈. (2)对比下面的两个图形,感受图形的转化,数图形中的圆圈个数可以有多种不同的方法.比如:前两层的圆圈个数和为(1+3)或22,由此得,1+3=22.据此总结规律,从1开始的n个连续奇数之和是多少?用含n的代数式把它表示出来:________. (3)运用(2)中的规律计算:41+43+45+…+199.
【解析】(1)由题知,第1层的圆圈个数为1=2×1-1;第2层的圆圈个数为3=2×2-1;第3层的圆圈个数为5=2×3-1;…,所以第n层的圆圈个数为(2n-1),当n=6时,2n-1=2×6-1=11(个),即第6层的圆圈个数为11.答案:11 (2n-1)
初中数学北师大版七年级上册3.5 探索与表达规律课文课件ppt: 这是一份初中数学北师大版七年级上册<a href="/sx/tb_c9926_t3/?tag_id=26" target="_blank">3.5 探索与表达规律课文课件ppt</a>,共17页。PPT课件主要包含了中间数的2倍,中间数的9倍,-2n,n+1,3n+1等内容,欢迎下载使用。
初中数学北师大版七年级上册3.5 探索与表达规律背景图ppt课件: 这是一份初中数学北师大版七年级上册3.5 探索与表达规律背景图ppt课件,共16页。PPT课件主要包含了知识要点,用代数式表示,a-7,a+8,a-8,a+6,a-6,a+7,a-1,a+1等内容,欢迎下载使用。
七年级上册第三章 整式及其加减3.5 探索与表达规律备课ppt课件: 这是一份七年级上册第三章 整式及其加减3.5 探索与表达规律备课ppt课件,共24页。PPT课件主要包含了学习目标,新课导入,新课讲解,课堂小结,当堂小练,拓展与延伸,布置作业,a+d=b+c,3n+1,3×2n-1-1等内容,欢迎下载使用。













