
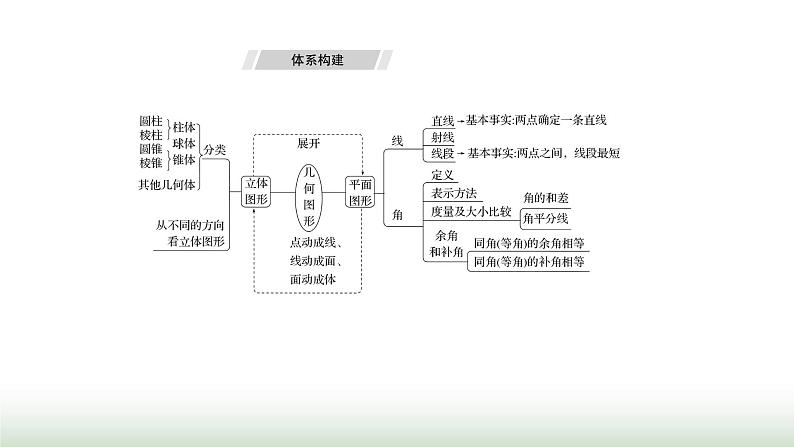


还剩19页未读,
继续阅读
所属成套资源:全套人教版七年级数学上册课时教学课件
成套系列资料,整套一键下载
人教版七年级数学上册第六章单元综合回顾课件
展开
这是一份人教版七年级数学上册第六章单元综合回顾课件,共27页。
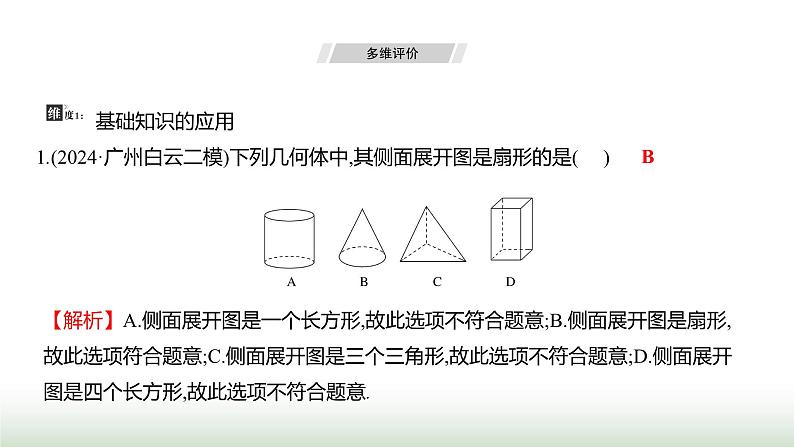
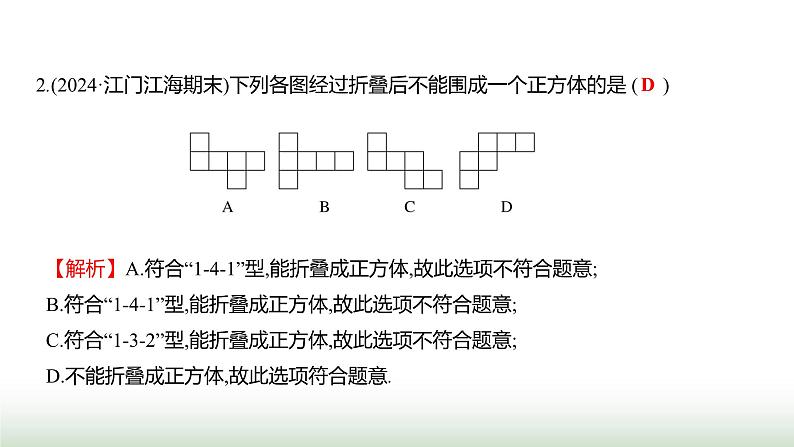
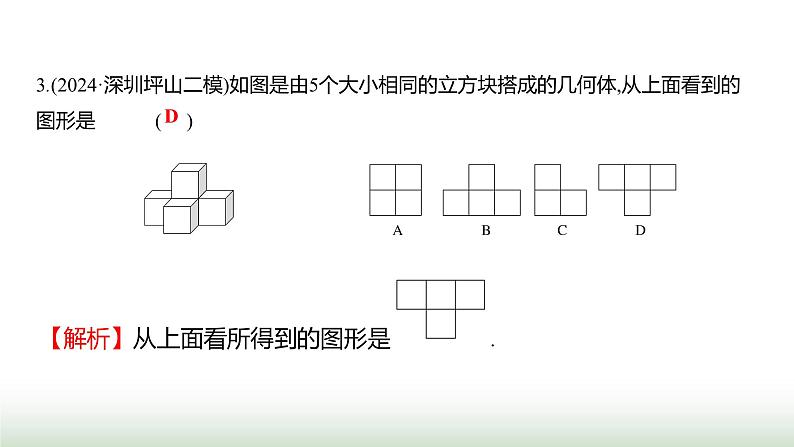
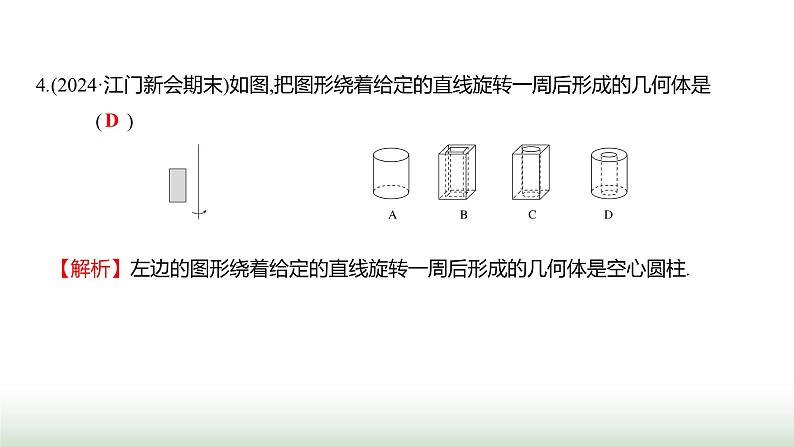
第六章 单元综合回顾 基础知识的应用1.(2024·广州白云二模)下列几何体中,其侧面展开图是扇形的是 ( )【解析】A.侧面展开图是一个长方形,故此选项不符合题意;B.侧面展开图是扇形,故此选项符合题意;C.侧面展开图是三个三角形,故此选项不符合题意;D.侧面展开图是四个长方形,故此选项不符合题意.B2.(2024·江门江海期末)下列各图经过折叠后不能围成一个正方体的是 ( )【解析】A.符合“1-4-1”型,能折叠成正方体,故此选项不符合题意;B.符合“1-4-1”型,能折叠成正方体,故此选项不符合题意;C.符合“1-3-2”型,能折叠成正方体,故此选项不符合题意;D.不能折叠成正方体,故此选项符合题意.D3.(2024·深圳坪山二模)如图是由5个大小相同的立方块搭成的几何体,从上面看到的图形是 ( )D4.(2024·江门新会期末)如图,把图形绕着给定的直线旋转一周后形成的几何体是 ( )【解析】左边的图形绕着给定的直线旋转一周后形成的几何体是空心圆柱.D5.(2024·广州番禺质检)在一张桌子上摆放着一些形状、大小都相同的碟子,从3个方向看到的图形如图所示,则这个桌子上的碟子总个数是 ( )A.11 B.12 C.13 D.14【解析】由从上面看到的图形可得:碟子共有3摞,由从前面看到的图形和从左面看到的图形,可得每摞碟子的个数,如图所示:故这张桌子上碟子的个数为3+4+5=12(个).B6.随着我国的发展与强大,中国文化与世界各国文化的交流与融合进一步加强.为了增进世界各国人民对中国语言和文化的理解,在世界各国建立孔子学院,推广汉语,传播中华文化.同时,各国学校之间的交流活动也逐年增加.在与国际友好学校交流活动中,小敏打算制作一个正方体礼盒送给外国朋友,每个面上分别书写一种中华传统美德,一共有“仁、义、礼、智、信、孝”六个字.如图是她设计的礼盒平面展开图,那么“礼”字对面的字是 ( )A.仁 B.义 C.智 D.信【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,“仁”与“礼”是相对面,“义”与“信”是相对面,“孝”与“智”是相对面.A C8.(方程思想)(2024·深圳宝安期中)若一个角等于它的补角的2倍,则这个角等于______度. 【解析】设这个角的度数为x,根据题意得x=2(180°-x),解得x=120°.9.(2024·肇庆怀集期末)如图,已知点C在点O的东北方向,点D在点O的北偏西20°方向,那么∠COD=________. 【解析】因为D在点O的北偏西20°方向,点C在点O的东北方向,所以∠COD=20°+45°=65°. 120 65° 10.(2024·河源和平期末)计算:32°45'+20°15'=________.【解析】32°45'+20°15'=52°60'=53°. 53° 基本技能(方法)、基本思想的应用11.(2024·深圳坪山期末)如图所示,C是线段AB上一点,且AB=3AC,P,Q从C点同时出发,分别朝着点A运动、点B运动,且点P的运动速度是点Q的一半,当AP=6 cm时,BQ的长为 ( )A.8 cm B.10 cmC.12 cm D.14 cmC【解析】因为AB=3AC,所以BC=2AC,设点P的运动速度是x,点Q的运动速度是2x,运动的时间为t,则CQ=2xt,CP=xt,因为AP=6 cm,所以AC=(6+xt)cm,所以BC=2(6+xt)cm,所以BQ=BC-CQ=2(6+xt)-2xt=12(cm). D13.(2024·广州期末)将一张长方形纸片按如图所示的方式折叠,BD,BE为折痕,若∠ABE=20°,则∠DBC为_______度. 【解析】根据翻折的性质可知,∠ABE=∠A'BE,∠DBC=∠DBC',又因为∠ABE+∠A'BE+∠DBC+∠DBC'=180°,所以∠ABE+∠DBC=90°,又因为∠ABE=20°,所以∠DBC=70°. 70 14.(2024·揭阳惠来质检)如图所示,∠DCE=90°,CF,CH,CG分别平分∠ACD,∠BCD,∠BCE,下列结论:①∠DCF+∠BCH=90°;②∠FCG=135°;③∠ECF+∠GCH=180°;④∠DCF-∠ECG=45°.其中正确的是___________. ①②④ 16.(分类讨论思想)(2024·广州期末)如图,线段AB=20 cm,C为AB的中点,点P从点A出发,以2 cm/s的速度沿线段AB向右运动,到点B停止;点Q从点B出发,以1 cm/s的速度沿线段AB向左运动,到点A停止.若P,Q两点同时出发,当其中一点停止运动时,另一点也随之停止.设点P的运动时间为x(x>0)s.(1)AC= cm. (2)是否存在某一时刻,使得C,P,Q这三点中,有一点恰为另外两点所连线段的中点?若存在,求出所有满足条件的x的值;若不存在,请说明理由. (2)存在.依题意得:AP=2x cm,BQ=x cm,由(1)可知:AC=BC=10 cm.分三种情况讨论:a.当点C为PQ的中点时,则PC=QC,如图①所示.因为PC=AC-AP=(10-2x) cm,QC=BC-BQ=(10-x) cm,所以10-2x=10-x,解得x=0(不符合题意,舍去);b.当点P为CQ的中点时,则PC=PQ,如图②所示.因为PC=AP-AC=(2x-10) cm,所以BP=AB-AP=(20-2x) cm,所以PQ=BP-BQ=20-2x-x=(20-3x) cm,所以2x-10=20-3x,解得x=6;c.当Q为PC的中点时,则PC=2CQ,如图③所示.因为PC=AP-AC=(2x-10) cm,CQ=BC-BQ=(10-x) cm,所以2x-10=2(10-x),解得x=7.5.综上所述,当x=6或7.5时,C,P,Q三点中,有一点恰为另外两点所连线段的中点.17.(2024·鹤山期末)(1)如图①所示,将长方形笔记本活页纸片的一角折过去,使角的顶点A落在A'处,BC为折痕.若∠ABC=54°,求∠A'BD的度数;(2)在(1)的条件下,如果将它的另一个角也斜折过去,并使BD边与BA'重合,折痕为BE,如图②所示,求∠D'BE和∠CBE的度数;(3)在图②中,若改变∠ABC的大小,则BA'的位置也随之改变,试判断当∠ABC的大小发生改变时,∠CBE的大小会不会改变,并说明理由. 实际生活生产中的运用18.(2024·梅州丰顺质检)如图,A,B两地间修建曲路与修建直路相比,虽然有利于游人更好地观赏风光,但增加了路程的长度.其中蕴含的数学道理是 ( )A.两点确定一条直线B.两点之间线段的长度,叫作这两点之间的距离C.两点之间有无数种连接方式D.两点之间,线段最短【解析】A,B两地间修建曲路与修建直路相比,虽然有利于游人更好地观赏风光,但增加了路程的长度.其中蕴含的数学道理是两点之间,线段最短.D
第六章 单元综合回顾 基础知识的应用1.(2024·广州白云二模)下列几何体中,其侧面展开图是扇形的是 ( )【解析】A.侧面展开图是一个长方形,故此选项不符合题意;B.侧面展开图是扇形,故此选项符合题意;C.侧面展开图是三个三角形,故此选项不符合题意;D.侧面展开图是四个长方形,故此选项不符合题意.B2.(2024·江门江海期末)下列各图经过折叠后不能围成一个正方体的是 ( )【解析】A.符合“1-4-1”型,能折叠成正方体,故此选项不符合题意;B.符合“1-4-1”型,能折叠成正方体,故此选项不符合题意;C.符合“1-3-2”型,能折叠成正方体,故此选项不符合题意;D.不能折叠成正方体,故此选项符合题意.D3.(2024·深圳坪山二模)如图是由5个大小相同的立方块搭成的几何体,从上面看到的图形是 ( )D4.(2024·江门新会期末)如图,把图形绕着给定的直线旋转一周后形成的几何体是 ( )【解析】左边的图形绕着给定的直线旋转一周后形成的几何体是空心圆柱.D5.(2024·广州番禺质检)在一张桌子上摆放着一些形状、大小都相同的碟子,从3个方向看到的图形如图所示,则这个桌子上的碟子总个数是 ( )A.11 B.12 C.13 D.14【解析】由从上面看到的图形可得:碟子共有3摞,由从前面看到的图形和从左面看到的图形,可得每摞碟子的个数,如图所示:故这张桌子上碟子的个数为3+4+5=12(个).B6.随着我国的发展与强大,中国文化与世界各国文化的交流与融合进一步加强.为了增进世界各国人民对中国语言和文化的理解,在世界各国建立孔子学院,推广汉语,传播中华文化.同时,各国学校之间的交流活动也逐年增加.在与国际友好学校交流活动中,小敏打算制作一个正方体礼盒送给外国朋友,每个面上分别书写一种中华传统美德,一共有“仁、义、礼、智、信、孝”六个字.如图是她设计的礼盒平面展开图,那么“礼”字对面的字是 ( )A.仁 B.义 C.智 D.信【解析】正方体的表面展开图,相对的面之间一定相隔一个正方形,“仁”与“礼”是相对面,“义”与“信”是相对面,“孝”与“智”是相对面.A C8.(方程思想)(2024·深圳宝安期中)若一个角等于它的补角的2倍,则这个角等于______度. 【解析】设这个角的度数为x,根据题意得x=2(180°-x),解得x=120°.9.(2024·肇庆怀集期末)如图,已知点C在点O的东北方向,点D在点O的北偏西20°方向,那么∠COD=________. 【解析】因为D在点O的北偏西20°方向,点C在点O的东北方向,所以∠COD=20°+45°=65°. 120 65° 10.(2024·河源和平期末)计算:32°45'+20°15'=________.【解析】32°45'+20°15'=52°60'=53°. 53° 基本技能(方法)、基本思想的应用11.(2024·深圳坪山期末)如图所示,C是线段AB上一点,且AB=3AC,P,Q从C点同时出发,分别朝着点A运动、点B运动,且点P的运动速度是点Q的一半,当AP=6 cm时,BQ的长为 ( )A.8 cm B.10 cmC.12 cm D.14 cmC【解析】因为AB=3AC,所以BC=2AC,设点P的运动速度是x,点Q的运动速度是2x,运动的时间为t,则CQ=2xt,CP=xt,因为AP=6 cm,所以AC=(6+xt)cm,所以BC=2(6+xt)cm,所以BQ=BC-CQ=2(6+xt)-2xt=12(cm). D13.(2024·广州期末)将一张长方形纸片按如图所示的方式折叠,BD,BE为折痕,若∠ABE=20°,则∠DBC为_______度. 【解析】根据翻折的性质可知,∠ABE=∠A'BE,∠DBC=∠DBC',又因为∠ABE+∠A'BE+∠DBC+∠DBC'=180°,所以∠ABE+∠DBC=90°,又因为∠ABE=20°,所以∠DBC=70°. 70 14.(2024·揭阳惠来质检)如图所示,∠DCE=90°,CF,CH,CG分别平分∠ACD,∠BCD,∠BCE,下列结论:①∠DCF+∠BCH=90°;②∠FCG=135°;③∠ECF+∠GCH=180°;④∠DCF-∠ECG=45°.其中正确的是___________. ①②④ 16.(分类讨论思想)(2024·广州期末)如图,线段AB=20 cm,C为AB的中点,点P从点A出发,以2 cm/s的速度沿线段AB向右运动,到点B停止;点Q从点B出发,以1 cm/s的速度沿线段AB向左运动,到点A停止.若P,Q两点同时出发,当其中一点停止运动时,另一点也随之停止.设点P的运动时间为x(x>0)s.(1)AC= cm. (2)是否存在某一时刻,使得C,P,Q这三点中,有一点恰为另外两点所连线段的中点?若存在,求出所有满足条件的x的值;若不存在,请说明理由. (2)存在.依题意得:AP=2x cm,BQ=x cm,由(1)可知:AC=BC=10 cm.分三种情况讨论:a.当点C为PQ的中点时,则PC=QC,如图①所示.因为PC=AC-AP=(10-2x) cm,QC=BC-BQ=(10-x) cm,所以10-2x=10-x,解得x=0(不符合题意,舍去);b.当点P为CQ的中点时,则PC=PQ,如图②所示.因为PC=AP-AC=(2x-10) cm,所以BP=AB-AP=(20-2x) cm,所以PQ=BP-BQ=20-2x-x=(20-3x) cm,所以2x-10=20-3x,解得x=6;c.当Q为PC的中点时,则PC=2CQ,如图③所示.因为PC=AP-AC=(2x-10) cm,CQ=BC-BQ=(10-x) cm,所以2x-10=2(10-x),解得x=7.5.综上所述,当x=6或7.5时,C,P,Q三点中,有一点恰为另外两点所连线段的中点.17.(2024·鹤山期末)(1)如图①所示,将长方形笔记本活页纸片的一角折过去,使角的顶点A落在A'处,BC为折痕.若∠ABC=54°,求∠A'BD的度数;(2)在(1)的条件下,如果将它的另一个角也斜折过去,并使BD边与BA'重合,折痕为BE,如图②所示,求∠D'BE和∠CBE的度数;(3)在图②中,若改变∠ABC的大小,则BA'的位置也随之改变,试判断当∠ABC的大小发生改变时,∠CBE的大小会不会改变,并说明理由. 实际生活生产中的运用18.(2024·梅州丰顺质检)如图,A,B两地间修建曲路与修建直路相比,虽然有利于游人更好地观赏风光,但增加了路程的长度.其中蕴含的数学道理是 ( )A.两点确定一条直线B.两点之间线段的长度,叫作这两点之间的距离C.两点之间有无数种连接方式D.两点之间,线段最短【解析】A,B两地间修建曲路与修建直路相比,虽然有利于游人更好地观赏风光,但增加了路程的长度.其中蕴含的数学道理是两点之间,线段最短.D
相关资料
更多









