人教版（2024）九年级上册24.1.1 圆练习题

这是一份人教版（2024）九年级上册24.1.1 圆练习题，共44页。

【题型1 直径所对圆周角为90°的运用】
【题型2 同弧或等弧所对的圆周角相等的运用】
【题型3 圆周角的度数等于它所对的弧上的圆心角的一半的运用】
【题型4 利用半径相等构成的等腰三角形有关运用】
【题型5 圆内接四边形的综合运用】
【题型6 运用圆周角、圆心角和圆内接四边形的性质求边长】
【题型1 直径所对圆周角为90°的运用】
1．（2023•香坊区校级开学）如图，AB是⊙O的直径，∠B＝30°，BC＝3，则AC的长为（ ）
A．B．C．1D．
2．（2022秋•建昌县期末）如图，以AB为直径的半圆O上有C，D的两点，，则∠BDC的度数为（ ）
A．30°B．35°C．45°D．60°
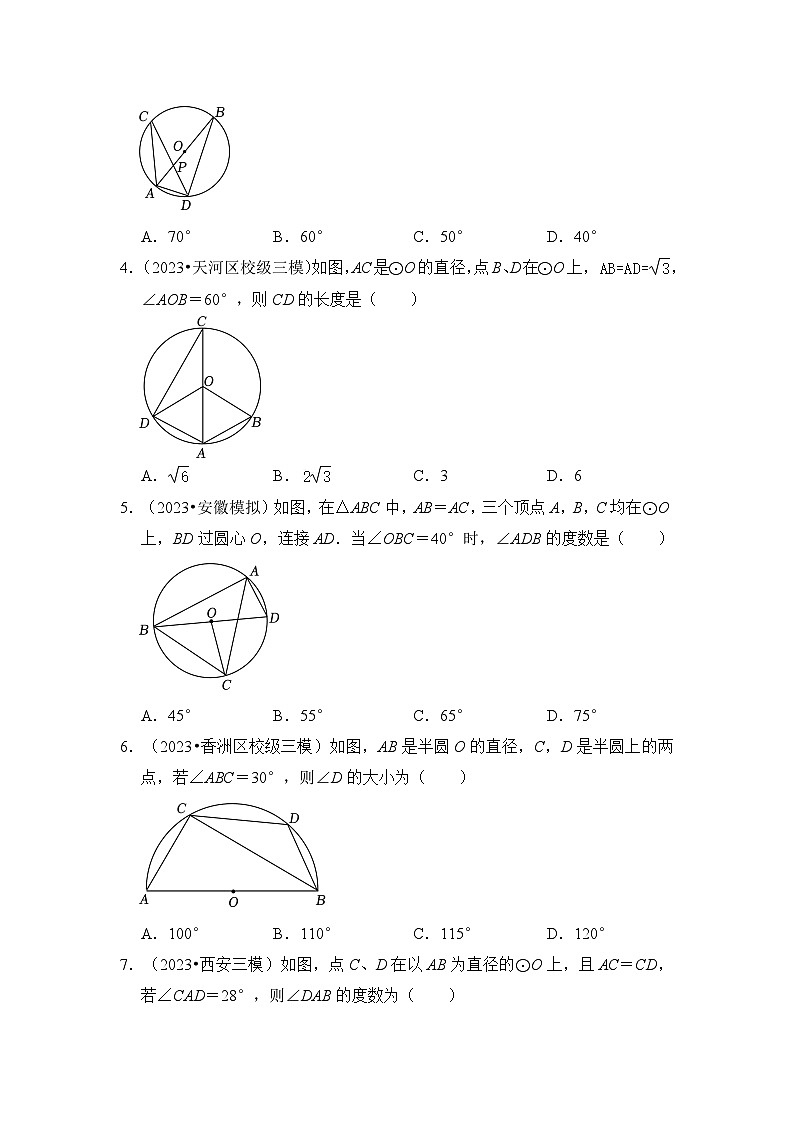
3．（2023•湖北）如图，在⊙O中，直径AB与弦CD相交于点P，连接AC，AD，BD，若∠C＝20°，∠BPC＝70°，则∠ADC＝（ ）
A．70°B．60°C．50°D．40°
4．（2023•天河区校级三模）如图，AC是⊙O的直径，点B、D在⊙O上，，∠AOB＝60°，则CD的长度是（ ）
A．B．C．3D．6
5．（2023•安徽模拟）如图，在△ABC中，AB＝AC，三个顶点A，B，C均在⊙O上，BD过圆心O，连接AD．当∠OBC＝40°时，∠ADB的度数是（ ）
A．45°B．55°C．65°D．75°
6．（2023•香洲区校级三模）如图，AB是半圆O的直径，C，D是半圆上的两点，若∠ABC＝30°，则∠D的大小为（ ）
A．100°B．110°C．115°D．120°
7．（2023•西安三模）如图，点C、D在以AB为直径的⊙O上，且AC＝CD，若∠CAD＝28°，则∠DAB的度数为（ ）
A．28°B．34°C．56°D．62°
8．（2023•湖北模拟）如图，△ABC是⊙O的内接三角形，AC是⊙O的直径，∠C＝50°，∠ABC的平分线BD交⊙O于点D，则∠BAD的度数是（ ）
A．80°B．85°C．90°D．95°
【题型2 同弧或等弧所对的圆周角相等的运用】
9．（2023•蒲城县二模）如图，AB是⊙O的直径，CD、BE是⊙O的两条弦，CD交AB于点G，点C是的中点，点B是的中点，若AB＝10，BG＝2，则BE的长为（ ）
A．3B．4C．6D．8
10．（2023•通榆县三模）如图，在⊙O中，∠AOB＝120°，C是劣弧AB的中点，P是优弧APB任意一点，连接AP，BP，则∠APC的度数是（ ）
A．30°或60°B．60°C．40°D．30°
11．（2023•凤翔县三模）如图，AB，CD是⊙O的两条直径，点E是劣弧的中点，连接BC，DE．若∠ABC＝32°，则∠CDE的度数为（ ）
A．34°B．29°C．32°D．24°
12．（2023•德惠市模拟）如图，在⊙O中，点C在上．若°，则∠BCD的度数为（ ）
A．55°B．70°C．110°D．250°
13．（2023•城厢区校级模拟）如图，在直径为AB的⊙O中，点C，D在圆上，AC＝CD，若∠CAD＝29°，则∠DAB的度数为（ ）
A．29°B．32°C．58°D．61°
14．（2023•鹿城区校级二模）如图，点A，B在以CD为直径的半圆上，B是的中点，连结BD，AC交于点E，若∠EDC＝25°，则∠ACD的度数是（ ）
​
A．30°B．35°C．40°D．45°
15．（2023•石景山区一模）如图，在⊙O中，C是的中点，点D是⊙O上一点．若∠ADC＝20°，则∠BOC的度数为（ ）
A．10°B．20°C．40°D．80°
16．（2023春•仓山区校级期中）如图，点A，B，C，D在⊙O上，∠AOC＝140°，B是弧AC的中点，则∠D的度数是（ ）
A．30°B．35°C．45°D．70°
【题型3 圆周角的度数等于它所对的弧上的圆心角的一半的运用】
17．（2023•长沙一模）如图，点A，B，C均在⊙O上，若∠A＝48°，∠C＝15°，则∠B＝（ ）
A．48°B．78°C．63°D．49°
18．（2023•乾安县二模）如图，在⊙O中，所对的圆周角∠ACB＝50°，若P为上一点，∠AOP＝55°，则∠POB的度数为（ ）
A．45°B．55°C．45°或155°D．55°或155°
19．（2023•临潼区三模）如图所示，点A，B，C，D在⊙O上，若四边形ABCO为平行四边形，连接BD与CD，则∠BDC的度数为（ ）
A．20°B．25°C．30°D．45°
20．（2023•绥中县一模）如图⊙O的半径为3，AB是弦，点C为弧AB的中点，若∠ABC＝30°，则弦AB的长为（ ）
A．B．3C．D．
21．（2023•新城区一模）如图，已知AB是⊙O的直径，C、D两点在⊙O上，∠ACD＝35°，则∠BOD的度数是（ ）
A．105°B．110°C．115°D．120°
22．（2023•潮南区二模）如图，已知BD是⊙O的直径，BD⊥AC于点E，∠AOC＝100°，则∠BDC的度数是（ ）
A．20°B．25°C．30°D．40°
23．（2023•平原县二模）如图，CD是⊙O的直径，弦AB⊥CD，若∠CDB＝28°，则∠AOC的度数为（ ）
A．28°B．56°C．58°D．62°
24．如图，在⊙O中，弦AB∥CD，若∠BOD＝80°，则∠ABC的度数为（ ）
A．20°B．40°C．50°D．80°
25．（2023•宜都市二模）如图，AB是⊙O的直径，C，D是⊙O上两点，若∠AOC＝140°，则∠BDC＝（ ）
A．20°B．40°C．55°D．70°
26．（2023•白山一模）如图，AB是⊙O的直径，点C、D在⊙O上，且在AB异侧，连接OC、CD、DA．若∠BOC＝130°，则∠D的大小是（ ）
A．15°B．25°C．35°D．50°
【题型4 利用半径相等构成的等腰三角形有关运用】
27．（2023•郧西县一模）如图，AB是⊙O的直径，C是⊙O上一点，D是AB另一侧半圆的中点，若CD＝3，BC＝4，则⊙O的半径长为（ ）
A．2B．C．2D．2
28．（2023春•汉寿县期中）如图，点A，B，C都在⊙O上，∠BAO＝20°，则∠ACB的大小是（ ）
A．90°B．70°C．60°D．40°
29．（2023•阜新模拟）如图，⊙O是△ABC的外接圆，已知∠ABO＝40°，则∠ACB的大小为（ ）
A．40°B．30°C．45°D．50°
30．（2023•新城区校级模拟）如图，△ABC 内接于⊙O，连接OB、OC，若OB＝AB，∠BAC＝110°，则∠ABC的度数为（ ）
A．60°B．40°C．30°D．20°
31．（2023•靖边县二模）如图，⊙O中，，连接AB，AC，BC，OB，OC，若∠ACB＝65°，则∠BOC的度数为（ ）
A．130°B．115°C．100°D．150°
32．（2023春•叙州区期中）如图，已知⊙O的直径CD⊥弦AB，垂足为E，∠ACD＝22.5°，若CD＝6，则AB的长为（ ）
A．4B．C．D．
33．（2023•姜堰区二模）如图，在⊙O中，CD为直径，弦AB∥CD，∠AOB＝40°，连接AC，则∠BAC等于（ ）
​
A．30°B．35°C．40°D．45°
34．（2023•袁州区校级二模）如图，点A、B、C在⊙O上，，则⊙O的半径为（ ）
A．B．C．6D．9
【题型5 圆内接四边形的综合运用】
35．（2023•泸县校级二模）如图，四边形ABCD内接于⊙O，连接BD．若，∠BDC＝50°，则∠ADB的度数是（ ）
A．65°B．70°C．75°D．80°
36．（2023•市北区三模）如图，四边形ABCD内接于⊙O，DA＝DC，∠CBE＝50°，∠AOD的大小为（ ）
A．130°B．100°C．120°D．110°
37．（2023•灞桥区校级模拟）如图，点A，B，C，D，E均在⊙O上，且BD经过圆心O，连接AB，AE，CE，若∠B+∠E
150°，则弧CD所对的圆心角的度数为（ ）
A．​30°B．40°C．50°D．60°
38．（2023•南关区校级模拟）如图，四边形ADBC内接于⊙O，四边形ADBO是平行四边形，则∠ABD的度数是（ ）
A．45°B．50°C．20°D．30°
39．（2023•赤峰）如图，圆内接四边形ABCD中，∠BCD＝105°，连接OB，OC，OD，BD，∠BOC＝2∠COD．则∠CBD的度数是（ ）
A．25°B．30°C．35°D．40°
40．（2023•金华模拟）在⊙O中，点A，B，C，D都在圆周上，OB∥DC，OD∥BC，则∠A的度数为（ ）
​
A．45°B．50°C．55°D．60°
【题型6 运用圆周角、圆心角和圆内接四边形的性质求边长】
41．（2023•雁塔区校级模拟）如图，点A、B、C、D在⊙O上，∠D＝120°，AB＝AC＝6，则点O到BC的距离是（ ）
A．3B．C．D．
42．（2023•温州）如图，四边形ABCD内接于⊙O，BC∥AD，AC⊥BD．若∠AOD＝120°，AD＝，则∠CAO的度数与BC的长分别为（ ）
A．10°，1B．10°，C．15°，1D．15°，
43．（2023•砀山县二模）如图，四边形ABCD内接于⊙O，且∠A＝90°，．若AB＝8，AD＝6，则BC的长为（ ）
A．B．5C．D．10
44．（2023•安次区一模）如图，四边形ABCD内接于⊙O，∠ABC＝135°，AC＝4，则⊙O的半径为（ ）
A．4B．2C．D．4
45．（2023•杭州二模）如图，四边形ABCD是⊙O的内接四边形，点F是CD延长线上的一点，且AD平分∠BDF，AE⊥CD于点E．
（1）求证：AB＝AC．
（2）若BD＝11，DE＝2，求CD的长．
46．（2023•浚县三模）如图，四边形ABCD是⊙O的内接四边形，且对角线BD经过⊙O的圆心O，过点A作AE⊥CD，与CD的延长线交于点E，且DA平分∠BDE．
（1）求证：∠ABO＝∠EAD；
（2）若⊙O的半径为5，CD＝6，求AD的长．
专题03 与圆有关的角和圆内接四边形
（4个考点6大类型）
【题型1 直径所对圆周角为90°的运用】
【题型2 同弧或等弧所对的圆周角相等的运用】
【题型3 圆周角的度数等于它所对的弧上的圆心角的一半的运用】
【题型4 利用半径相等构成的等腰三角形有关运用】
【题型5 圆内接四边形的综合运用】
【题型6 运用圆周角、圆心角和圆内接四边形的性质求边长】
【题型1 直径所对圆周角为90°的运用】
1．（2023•香坊区校级开学）如图，AB是⊙O的直径，∠B＝30°，BC＝3，则AC的长为（ ）
A．B．C．1D．
【答案】A
【解答】解：∵AB是⊙O的直径，
∴∠ACB＝90°，
∵∠B＝30°，
∵tanB＝＝tan30°＝，BC＝3，
∴AC＝．
故选：A．
2．（2022秋•建昌县期末）如图，以AB为直径的半圆O上有C，D的两点，，则∠BDC的度数为（ ）
A．30°B．35°C．45°D．60°
【答案】C
【解答】解：∵弧AC＝弧BC，
∴∠AOC＝∠BOC＝90°，
∴，
故选：C．
3．（2023•湖北）如图，在⊙O中，直径AB与弦CD相交于点P，连接AC，AD，BD，若∠C＝20°，∠BPC＝70°，则∠ADC＝（ ）
A．70°B．60°C．50°D．40°
【答案】D
【解答】解：∵∠C＝20°，∠BPC＝70°，
∴∠BAC＝∠BPC﹣∠C＝50°＝∠BDC，
∵AB是⊙O的直径，
∴∠ADB＝90°，
∴∠ADC＝∠ADB﹣∠BDC＝40°，
故选：D．
4．（2023•天河区校级三模）如图，AC是⊙O的直径，点B、D在⊙O上，，∠AOB＝60°，则CD的长度是（ ）
A．B．C．3D．6
【答案】C
【解答】解：∵AB＝AD，
∴∠AOD＝∠AOB＝60°，
∵OD＝OC，
∴，
在Rt△ACD中，，
即，
∴CD＝3，
故选：C．
5．（2023•安徽模拟）如图，在△ABC中，AB＝AC，三个顶点A，B，C均在⊙O上，BD过圆心O，连接AD．当∠OBC＝40°时，∠ADB的度数是（ ）
A．45°B．55°C．65°D．75°
【答案】C
【解答】解：∵BD是⊙O的直径，
∴∠BAD＝90°，
∵∠CAD＝∠OBC＝40°，
∴∠BAC＝50°，
∵AB＝AC，
∴，
∴∠ABD＝25°，
∴∠ADB＝65°．
故选：C．
6．（2023•香洲区校级三模）如图，AB是半圆O的直径，C，D是半圆上的两点，若∠ABC＝30°，则∠D的大小为（ ）
A．100°B．110°C．115°D．120°
【答案】D
【解答】解：∵AB是半圆O的直径，
∴∠ACB＝90°，
∴∠A＝90°﹣∠ABC＝90°﹣30°＝60°，
∵四边形ABDC为⊙O的内接四边形，
∴∠A+∠D＝180°，
∴∠D＝180°﹣60°＝120°．
故选：D．
7．（2023•西安三模）如图，点C、D在以AB为直径的⊙O上，且AC＝CD，若∠CAD＝28°，则∠DAB的度数为（ ）
A．28°B．34°C．56°D．62°
【答案】B
【解答】解：∵AC＝CD，∠CAD＝28°，
∴∠CAD＝∠CDA＝28°，
∴∠ACD＝180°﹣∠CAD﹣∠CDA＝124°，
∵四边形ABCD是⊙O的内接四边形，
∴∠ACD+∠ABD＝180°，
∴∠ABD＝180°﹣∠ACD＝56°，
∵AB是⊙O的直径，
∴∠ADB＝90°，
∴∠DAB＝90°﹣∠ABD＝34°，
故选：B．
8．（2023•湖北模拟）如图，△ABC是⊙O的内接三角形，AC是⊙O的直径，∠C＝50°，∠ABC的平分线BD交⊙O于点D，则∠BAD的度数是（ ）
A．80°B．85°C．90°D．95°
【答案】B
【解答】解：∵AC是⊙O的直径，
∴∠ABC＝90°，
∵∠C＝50°，
∴∠BAC＝40°，
∵∠ABC的平分线是BD，
∴∠CBD＝45°，
∵∠CBD＝∠CAD，
∴∠CAD＝45°，
∴∠BAD＝∠BAC+∠CAD＝40°+45°＝85°．
故选：B．
【题型2 同弧或等弧所对的圆周角相等的运用】
9．（2023•蒲城县二模）如图，AB是⊙O的直径，CD、BE是⊙O的两条弦，CD交AB于点G，点C是的中点，点B是的中点，若AB＝10，BG＝2，则BE的长为（ ）
A．3B．4C．6D．8
【答案】D
【解答】解：连接OD，如图，
∵点C是的中点，点B是的中点，
∴＝＝，CD⊥AB，
∴BE＝CD，CG＝DG，
∵AB＝10，AB是⊙O的直径，
∴OB＝OD＝5，
∵BG＝2，
∴OG＝OB﹣BG＝3，
在Rt△ODG中，OG＝3，OD＝5，
∴DG＝＝4，
∴CD＝2DG＝8，
∴BE＝8，
故选：D．
10．（2023•通榆县三模）如图，在⊙O中，∠AOB＝120°，C是劣弧AB的中点，P是优弧APB任意一点，连接AP，BP，则∠APC的度数是（ ）
A．30°或60°B．60°C．40°D．30°
【答案】D
【解答】解：在⊙O中，∠AOB＝120°，
∴∠APB＝＝120°＝60°，
∵C是劣弧AB的中点，
∴∠APC＝APB＝60°＝30°．
故选：D．
11．（2023•凤翔县三模）如图，AB，CD是⊙O的两条直径，点E是劣弧的中点，连接BC，DE．若∠ABC＝32°，则∠CDE的度数为（ ）
A．34°B．29°C．32°D．24°
【答案】B
【解答】解：连接OE，如图，
∵∠ABC＝32°，
∴∠AOC＝2∠ABC＝64°，
∴∠BOC＝180°﹣∠AOC＝116°，
∵点E是劣弧的中点，
∴∠COE＝∠BOE＝∠BOC＝58°，
∴∠CDE＝∠COE＝29°．
故选：B．
12．（2023•德惠市模拟）如图，在⊙O中，点C在上．若°，则∠BCD的度数为（ ）
A．55°B．70°C．110°D．250°
【答案】A
【解答】解：∵°，
∴∠BCD＝∠AOB＝×110°＝55°．
故选：A．
13．（2023•城厢区校级模拟）如图，在直径为AB的⊙O中，点C，D在圆上，AC＝CD，若∠CAD＝29°，则∠DAB的度数为（ ）
A．29°B．32°C．58°D．61°
【答案】B
【解答】解：∵AC＝CD，
∴∠ADC＝∠CAD＝29°，
∴∠ACD＝180°﹣29°﹣29°＝122°，
∵AB是⊙O的直径，
∴∠ACB＝90°，
∴∠BCD＝∠ACD﹣∠ACB＝122°﹣90°＝32°，
∴∠DAB＝∠BCD＝32°，
故选：B．
14．（2023•鹿城区校级二模）如图，点A，B在以CD为直径的半圆上，B是的中点，连结BD，AC交于点E，若∠EDC＝25°，则∠ACD的度数是（ ）
​
A．30°B．35°C．40°D．45°
【答案】C
【解答】解：连接AD，
∵CD是圆的直径，
∴∠DAC＝90°，
∵B是的中点，
∴∠CDE＝∠EDA＝25°，
∴∠ADC＝50°，
∴∠ACD＝90°﹣∠ADC＝40°．
故选：C．
15．（2023•石景山区一模）如图，在⊙O中，C是的中点，点D是⊙O上一点．若∠ADC＝20°，则∠BOC的度数为（ ）
A．10°B．20°C．40°D．80°
【答案】C
【解答】解：∵C是的中点，
∴，
∵∠ADC＝20°，
∴∠BOC＝2∠ADC＝40°，
故选：C．
16．（2023春•仓山区校级期中）如图，点A，B，C，D在⊙O上，∠AOC＝140°，B是弧AC的中点，则∠D的度数是（ ）
A．30°B．35°C．45°D．70°
【答案】B
【解答】解：连接OB，如图，
∵B是弧AC的中点，
即＝，
∴∠AOB＝∠COB＝∠AOC＝×140°＝70°，
∵∠D和∠AOB都对，
∴∠D＝∠AOB＝35°．
故选：B．
【题型3 圆周角的度数等于它所对的弧上的圆心角的一半的运用】
17．（2023•长沙一模）如图，点A，B，C均在⊙O上，若∠A＝48°，∠C＝15°，则∠B＝（ ）
A．48°B．78°C．63°D．49°
【答案】C
【解答】解：如图，连接OA，
∵OA＝OC，
∴∠OAC＝∠C＝15°，
∵∠BAC＝48°，
∴∠OAB＝48°+15°＝63°，
∵OA＝OB，
∴∠B＝∠OAB＝63°．
故选：C．
18．（2023•乾安县二模）如图，在⊙O中，所对的圆周角∠ACB＝50°，若P为上一点，∠AOP＝55°，则∠POB的度数为（ ）
A．45°B．55°C．45°或155°D．55°或155°
【答案】A
【解答】解：∵∠ACB＝50°，∠ACB＝∠AOB，
∴∠AOB＝100°，
∴∠AOP+∠BOP＝100°，
∵∠AOP＝55°，
∴∠POB＝45°．
故选：A．
19．（2023•临潼区三模）如图所示，点A，B，C，D在⊙O上，若四边形ABCO为平行四边形，连接BD与CD，则∠BDC的度数为（ ）
A．20°B．25°C．30°D．45°
【答案】C
【解答】解：连接OB，
∵四边形ABCO为平行四边形，
∴OA＝BC，
∵OA＝OB＝OC，
∴OB＝OC＝BC，
∴△OBC是等边三角形，
∴∠BOC＝60°，
∴∠BDC＝∠BOC＝30°．
故选：C．
20．（2023•绥中县一模）如图⊙O的半径为3，AB是弦，点C为弧AB的中点，若∠ABC＝30°，则弦AB的长为（ ）
A．B．3C．D．
【答案】D
【解答】解：连接OA、OC，OC与AB交于点D，
∵点C为 的中点，
∴OD⊥AB，AB＝2AD，
∵∠ABC＝30°，
∴∠AOC＝2∠ABC＝60°，
在Rt△OAD中，，
∴．
故选：D．
21．（2023•新城区一模）如图，已知AB是⊙O的直径，C、D两点在⊙O上，∠ACD＝35°，则∠BOD的度数是（ ）
A．105°B．110°C．115°D．120°
【答案】B
【解答】解：∵∠ACD与∠AOD都对着，
∴∠AOD＝2∠ACD，
而∠ACD＝35°，
∴∠AOD＝70°，
∴∠BOD＝180°﹣70°＝110°．
故选：B．
22．（2023•潮南区二模）如图，已知BD是⊙O的直径，BD⊥AC于点E，∠AOC＝100°，则∠BDC的度数是（ ）
A．20°B．25°C．30°D．40°
【答案】B
【解答】解：∵BD⊥AC，∠AOC＝100°，
∴∠BOC＝∠AOC＝50°，
则∠BDC＝∠BOC＝25°，
故选：B．
23．（2023•平原县二模）如图，CD是⊙O的直径，弦AB⊥CD，若∠CDB＝28°，则∠AOC的度数为（ ）
A．28°B．56°C．58°D．62°
【答案】B
【解答】解：∵CD是⊙O的直径，弦AB⊥CD，
∴＝，
∵∠CDB＝28°，
∴∠AOC＝2∠CDB＝56°，
故选：B．
24．如图，在⊙O中，弦AB∥CD，若∠BOD＝80°，则∠ABC的度数为（ ）
A．20°B．40°C．50°D．80°
【答案】B
【解答】解：∵∠BOD＝80°，
∴∠BCD＝∠BOD＝40°，
∵AB∥CD，
∴∠ABC＝∠BCD＝40°．
故选：B．
25．（2023•宜都市二模）如图，AB是⊙O的直径，C，D是⊙O上两点，若∠AOC＝140°，则∠BDC＝（ ）
A．20°B．40°C．55°D．70°
【答案】A
【解答】解：∵∠BOC+∠AOC＝180°，∠AOC＝140°，
∴∠BOC＝180°﹣140°＝40°，
∴∠BDC＝∠BOC＝20°．
故选：A．
26．（2023•白山一模）如图，AB是⊙O的直径，点C、D在⊙O上，且在AB异侧，连接OC、CD、DA．若∠BOC＝130°，则∠D的大小是（ ）
A．15°B．25°C．35°D．50°
【答案】B
【解答】解：∵∠BOC+∠AOC＝180°，
∴∠AOC＝180°﹣∠BOC＝50°．
∴∠D＝∠AOC＝25°．
故选：B．
【题型4 利用半径相等构成的等腰三角形有关运用】
27．（2023•郧西县一模）如图，AB是⊙O的直径，C是⊙O上一点，D是AB另一侧半圆的中点，若CD＝3，BC＝4，则⊙O的半径长为（ ）
A．2B．C．2D．2
【答案】B
【解答】解：连接AD，过点B作BE⊥CD于点E，
∵AB是⊙O的直径，D是的中点，
∴∠ADB＝90°，AD＝DB，
∴△ADB是等腰直角三角形，
∴∠A＝∠ABD＝45°，
∴∠C＝∠A＝45°，
∴△EBC是等腰直角三角形，
∵BC＝4，
∴EC＝EB＝2，
∵CD＝3，
∴DE＝，
∴BD＝＝＝，
在等腰直角△BDA中，AB＝＝2，
∴⊙O的半径长为，
故选：B．
28．（2023春•汉寿县期中）如图，点A，B，C都在⊙O上，∠BAO＝20°，则∠ACB的大小是（ ）
A．90°B．70°C．60°D．40°
【答案】B
【解答】解：∵AO＝OB，
∴△AOB是等腰三角形，
∵∠BAO＝20°，
∴∠OBA＝20°，即∠AOB＝140°，
∵∠AOB＝2∠ACB，
∴∠ACB＝70°．
故选：B．
29．（2023•阜新模拟）如图，⊙O是△ABC的外接圆，已知∠ABO＝40°，则∠ACB的大小为（ ）
A．40°B．30°C．45°D．50°
【答案】D
【解答】解：△AOB中，OA＝OB，∠ABO＝40°；
∴∠AOB＝180°﹣2∠ABO＝100°；
∴∠ACB＝∠AOB＝×100°＝50°．
故选：D．
30．（2023•新城区校级模拟）如图，△ABC 内接于⊙O，连接OB、OC，若OB＝AB，∠BAC＝110°，则∠ABC的度数为（ ）
A．60°B．40°C．30°D．20°
【答案】B
【解答】解：连接OA，
∵OA＝OB＝AB，
∴△OAB是等边三角形，
∠OAB＝60°，
∵∠BAC＝110°，
∴∠OAC＝∠OCA＝50°，
∴∠AOC＝180°﹣∠OAC﹣∠OCA＝80°，
∴∠ABC＝∠AOC＝40°．
故选：B．
31．（2023•靖边县二模）如图，⊙O中，，连接AB，AC，BC，OB，OC，若∠ACB＝65°，则∠BOC的度数为（ ）
A．130°B．115°C．100°D．150°
【答案】C
【解答】解：∵，
∴∠ACB＝∠ABC＝65°，
∴∠A＝180°﹣∠ABC﹣∠ACB＝50°，
∴∠BOC＝2∠A＝100°，
故选：C．
32．（2023春•叙州区期中）如图，已知⊙O的直径CD⊥弦AB，垂足为E，∠ACD＝22.5°，若CD＝6，则AB的长为（ ）
A．4B．C．D．
【答案】C
【解答】解：连结OA，
∵∠ACD＝22.5°，
∴∠AOD＝2∠ACD＝45°，
∵⊙O的直径CD⊥弦AB，
∴AE＝BE，
∴△OAE为等腰直角三角形，
∴AE＝OA•sin45°＝OA，
∵CD＝6，
∴OA＝3，
∴AE＝，
∴AB＝2AE＝．
故选：C．
33．（2023•姜堰区二模）如图，在⊙O中，CD为直径，弦AB∥CD，∠AOB＝40°，连接AC，则∠BAC等于（ ）
​
A．30°B．35°C．40°D．45°
【答案】B
【解答】解：∵OA＝OB，
∴∠OAB＝∠OBA，
∵∠AOB＝40°，
∴∠OAB＝70°，
∵弦AB∥CD，
∴∠AOD＝∠OAB＝70°，
∴∠C＝∠AOD＝35°，
∵AB∥CD，
∴∠BAC＝∠C＝35°．
故选：B．
34．（2023•袁州区校级二模）如图，点A、B、C在⊙O上，，则⊙O的半径为（ ）
A．B．C．6D．9
【答案】C
【解答】解：如图所示，过点O作OD⊥AB于点D，则，
∵，
∴∠AOB＝2∠ACB＝120°，则∠OAB＝30°，
∵OA＝OB，OD⊥AB，
∴AD＝DB，
在Rt△AOD中，
∴
∴，
故选：C
【题型5 圆内接四边形的综合运用】
35．（2023•泸县校级二模）如图，四边形ABCD内接于⊙O，连接BD．若，∠BDC＝50°，则∠ADB的度数是（ ）
A．65°B．70°C．75°D．80°
【答案】D
【解答】解：∵＝，∠BDC＝50°，
∴∠ABC＝∠BDC＝50°，
∵四边形ABCD内接于⊙O，
∴∠ADC+∠ABC＝180°，
∴∠ADC＝180°﹣∠ABC＝130°，
∴∠ADB＝∠ADC﹣∠BDC＝130°﹣50°＝80°，
故选：D．
36．（2023•市北区三模）如图，四边形ABCD内接于⊙O，DA＝DC，∠CBE＝50°，∠AOD的大小为（ ）
A．130°B．100°C．120°D．110°
【答案】A
【解答】解：∵∠ADC+∠ABC＝180°，∠ABC+∠CBE＝180°，
∴∠ADC＝∠CBE＝50°，
∵DA＝DC，
∴∠DAC＝∠DCA＝（180°﹣50°）＝65°，
∴∠AOD＝2∠ACD＝130°，
故选：A．
37．（2023•灞桥区校级模拟）如图，点A，B，C，D，E均在⊙O上，且BD经过圆心O，连接AB，AE，CE，若∠B+∠E
150°，则弧CD所对的圆心角的度数为（ ）
A．​30°B．40°C．50°D．60°
【答案】D
【解答】解：连接BC、OC，
∵四边形ABCE为⊙O的内接四边形，
∴∠ABC+∠E＝180°，
∵∠ABD+∠E＝150°，
∴∠CBD＝30°，
∴∠COD＝60°，即弧CD所对的圆心角的度数为60°，
故选：D．
38．（2023•南关区校级模拟）如图，四边形ADBC内接于⊙O，四边形ADBO是平行四边形，则∠ABD的度数是（ ）
A．45°B．50°C．20°D．30°
【答案】D
【解答】解：∵四边形ADBC内接于⊙O，
∴∠C+∠D＝180°，
∵四边形ADBO是平行四边形，
∴∠AOB＝∠D，
∵∠C＝∠AOB，
∴∠D+∠D＝180°，
解得∠D＝120°，
∵四边形ADBO是平行四边形，OA＝OB，
∴四边形ADBO是菱形，
∴DA＝DB，
∴∠ABD＝∠BAD＝×（180°﹣120°）＝30°．
故选：D．
39．（2023•赤峰）如图，圆内接四边形ABCD中，∠BCD＝105°，连接OB，OC，OD，BD，∠BOC＝2∠COD．则∠CBD的度数是（ ）
A．25°B．30°C．35°D．40°
【答案】A
【解答】解：∵四边形ABCD是⊙O的内接四边形，
∴∠A+∠BCD＝180°，
∵∠BCD＝105°，
∴∠A＝75°，
∴∠BOD＝2∠A＝150°，
∵∠BOC＝2∠COD，
∴∠BOD＝3∠COD＝150°，
∴∠COD＝50°，
∴∠CBD＝∠COD＝25°，
故选：A．
40．（2023•金华模拟）在⊙O中，点A，B，C，D都在圆周上，OB∥DC，OD∥BC，则∠A的度数为（ ）
​
A．45°B．50°C．55°D．60°
【答案】D
【解答】解：∵点A，B，C，D都在圆周上，
∴∠C+∠A＝180°，
∵OB∥DC，OD∥BC，
∴∠C+∠OBC＝180°，∠BOD+∠OBC＝180°，
∴∠C＝∠BOD，
∵∠BOD＝2∠A，
∴∠C＝2∠A，
即3∠A＝180°，
∴∠A＝60°，
故选：D．
【题型6 运用圆周角、圆心角和圆内接四边形的性质求边长】
41．（2023•雁塔区校级模拟）如图，点A、B、C、D在⊙O上，∠D＝120°，AB＝AC＝6，则点O到BC的距离是（ ）
A．3B．C．D．
【答案】B
【解答】解：过点O作OE⊥BC于点E，连接OB、OC，
∵四边形ABDC是圆内接四边形，
∴∠A+∠D＝180°，
∵∠D＝120°，
∴∠A＝60°，
∴∠BOC＝120°，
∵OB＝OC，OE⊥BC，
∴∠COE＝∠BOE＝60°，
∵AB＝AC＝6，∠A＝60°，
∴△ABC是等边三角形，
∴BC＝AB＝AC＝6，
∵OE⊥BC，
∴BE＝CE＝3，
∴，
即，
解得：，
即点O到BC的距离是，
故选：B．
42．（2023•温州）如图，四边形ABCD内接于⊙O，BC∥AD，AC⊥BD．若∠AOD＝120°，AD＝，则∠CAO的度数与BC的长分别为（ ）
A．10°，1B．10°，C．15°，1D．15°，
【答案】C
【解答】解：∵BC∥AD，
∴∠DBC＝∠ADB，
∴＝，
∴∠AOB＝∠COD，∠CAD＝∠BDA，
∵DB⊥AC，
∴∠AED＝90°，
∴∠CAD＝∠BDA＝45°，
∴∠AOB＝2∠ADB＝90°，∠COD＝2∠CAD＝90°，
∵∠AOD＝120°，
∴∠BOC＝360°﹣90°﹣90°﹣120°＝60°，
∵OB＝OC，
∴△OBC是等边三角形，
∴BC＝OB，
∵OA＝OD，∠AOD＝120°，
∴∠OAD＝∠ODA＝30°，
∴AD＝OA＝，
∴OA＝1，
∴BC＝1，
∴∠CAO＝∠CAD﹣∠OAD＝45°﹣30°＝15°．
故选：C．
43．（2023•砀山县二模）如图，四边形ABCD内接于⊙O，且∠A＝90°，．若AB＝8，AD＝6，则BC的长为（ ）
A．B．5C．D．10
【答案】A
【解答】解：如图所示，连接BD，
∵∠A＝90°，AB＝8，AD＝6，
∴，
∵四边形ABCD内接于⊙O，∠A＝90°，
∴∠BCD＝90°，
∵．
∴BC＝CD＝，
故选：A．
44．（2023•安次区一模）如图，四边形ABCD内接于⊙O，∠ABC＝135°，AC＝4，则⊙O的半径为（ ）
A．4B．2C．D．4
【答案】B
【解答】解：连接OA，OC，
∵四边形ABCD内接于⊙O，∠ABC＝135°，
∴∠ADC＝45°，
∴∠AOC＝90°，
由勾股定理得：OA2+OC2＝AC2，
∵OA＝OC，AC＝4，
∴，
∴⊙O的半径为：．
故选：B．
45．（2023•杭州二模）如图，四边形ABCD是⊙O的内接四边形，点F是CD延长线上的一点，且AD平分∠BDF，AE⊥CD于点E．
（1）求证：AB＝AC．
（2）若BD＝11，DE＝2，求CD的长．
【答案】见试题解答内容
【解答】（1）证明：∵AD平分∠BDF，
∴∠ADF＝∠ADB，
∵∠ABC+∠ADC＝180°，∠ADC+∠ADF＝180°，
∴∠ADF＝∠ABC，
∵∠ACB＝∠ADB，
∴∠ABC＝∠ACB，
∴AB＝AC；
（2）解：过点A作AG⊥BD，垂足为点G．
∵AD平分∠BDF，AE⊥CF，AG⊥BD，
∴AG＝AE，∠AGB＝∠AEC＝90°，
在Rt△AED和Rt△AGD中，
，
∴Rt△AED≌Rt△AGD，
∴GD＝ED＝2，
在Rt△AEC和Rt△AGB中，
，
∴Rt△AEC≌Rt△AGB（HL），
∴BG＝CE，
∵BD＝11，
∴BG＝BD﹣GD＝11﹣2＝9，
∴CE＝BG＝9，
∴CD＝CE﹣DE＝9﹣2＝7．
46．（2023•浚县三模）如图，四边形ABCD是⊙O的内接四边形，且对角线BD经过⊙O的圆心O，过点A作AE⊥CD，与CD的延长线交于点E，且DA平分∠BDE．
（1）求证：∠ABO＝∠EAD；
（2）若⊙O的半径为5，CD＝6，求AD的长．
【答案】（1）见解答；
（2）2．
【解答】（1）证明：∵BD为直径，
∴∠BAD＝90°，
∴∠ABD+∠ADB＝90°，
∵AE⊥CE，
∴∠ADE+∠EAD＝90°，
∵DA平分∠BDE，
∴∠ADB＝∠ADE，
∴∠ABD＝∠EAD，
即∠ABO＝∠EAD；
（2）解：过O点作OH⊥CD于H点，连接OA，如图，则CH＝DH＝CD＝3，
在Rt△ODH中，OH＝＝＝4，
∵OA＝OD，
∴∠ODA＝∠OAD，
∵∠ODA＝∠ADE，
∴∠OAD＝∠ADE，
∴OA∥CE，
∴∠OAE＝180°﹣∠E＝90°，
∵∠OHE＝∠E＝∠OAE＝90°，
∴四边形OAEH为矩形，
∴AE＝OH＝4，HE＝OA＝5，
∴DE＝5﹣3＝2，
在Rt△ADE中，AD＝＝＝2．