人教版九年级数学上册重难点专题提优训练专题03反比例函数与几何图形的综合应用(原卷版+解析)

这是一份人教版九年级数学上册重难点专题提优训练专题03反比例函数与几何图形的综合应用(原卷版+解析)，共66页。试卷主要包含了反比例函数与三角形的综合应用，反比例函数与矩形的综合应用，反比例函数与正方形的综合应用，反比例函数与菱形的综合应用等内容，欢迎下载使用。
考点一 反比例函数与三角形的综合应用 考点二 反比例函数与平行四边形的综合应用
考点三 反比例函数与矩形的综合应用 考点四 反比例函数与菱形的综合应用
考点五 反比例函数与正方形的综合应用
考点一 反比例函数与三角形的综合应用
例题：（2022·贵州黔东南·中考真题）如图，在平面直角坐标系中，等腰直角三角形的斜边轴于点，直角顶点在轴上，双曲线经过边的中点，若，则______．
【变式训练】
1．（2022·山东东营·中考真题）如图，是等腰直角三角形，直角顶点与坐标原点重合，若点B在反比例函数的图象上，则经过点A的反比例函数表达式为____________．
2．（2022·江苏·淮安市淮安区教师发展中心学科研训处模拟预测）如图，把一个等腰直角三角形ACB放在平面直角坐标系中，∠ACB＝90°，点C(﹣2,0)，点B在反比例函数的图象上，且y轴平分∠BAC，则k的值是________．
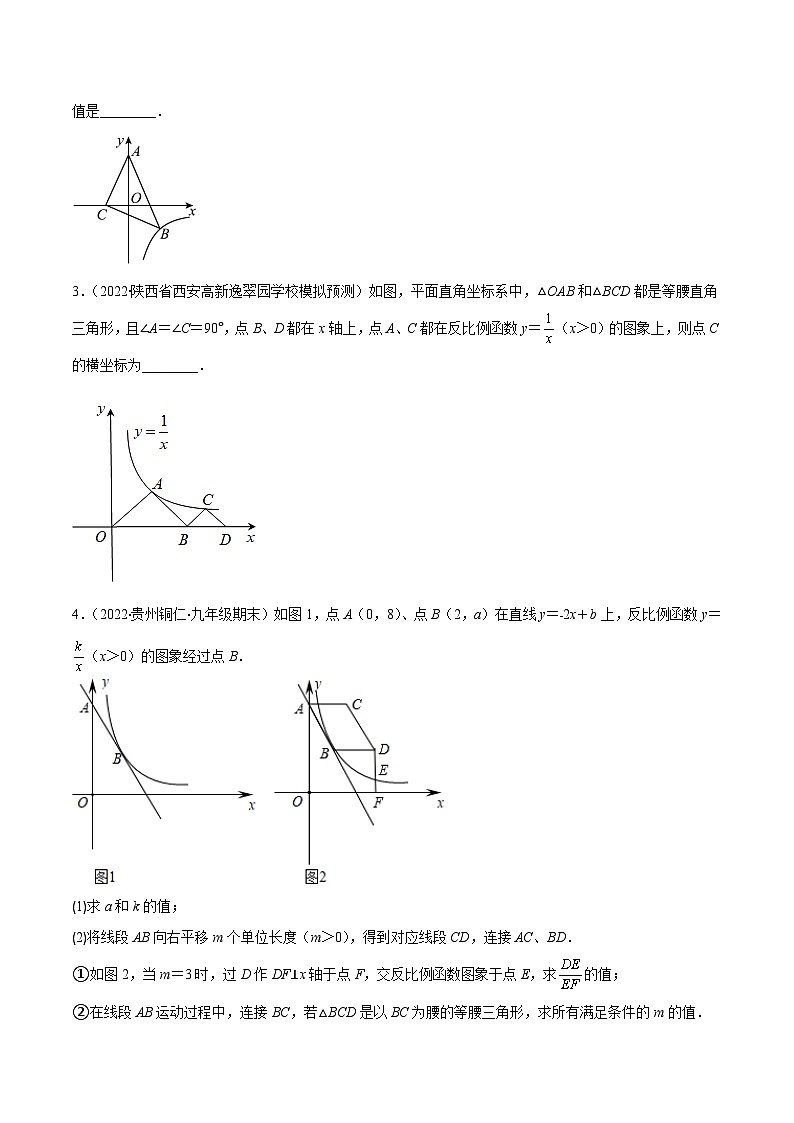
3．（2022·陕西省西安高新逸翠园学校模拟预测）如图，平面直角坐标系中，△OAB和△BCD都是等腰直角三角形，且∠A＝∠C＝90°，点B、D都在x轴上，点A、C都在反比例函数y＝（x＞0）的图象上，则点C的横坐标为________．
4．（2022·贵州铜仁·九年级期末）如图1，点A（0，8）、点B（2，a）在直线y＝﹣2x＋b上，反比例函数y＝（x＞0）的图象经过点B．
(1)求a和k的值；
(2)将线段AB向右平移m个单位长度（m＞0），得到对应线段CD，连接AC、BD．
①如图2，当m＝3时，过D作DF⊥x轴于点F，交反比例函数图象于点E，求的值；
②在线段AB运动过程中，连接BC，若△BCD是以BC为腰的等腰三角形，求所有满足条件的m的值．
5．（2022·四川遂宁·八年级期末）如图（1），在平面直角坐标系中，将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，点C坐标为（﹣1，0），点A的坐标为（0，2），一次函数y＝kx+b的图象经过点B，C，反比例函数图象也经过点B．
(1)求反比例函数的关系式；
(2)如图（2），M是线段AB上一点，连接OM交AC于点N，△AMN与△CON的面积相等，求出点M的坐标．
(3)若P是y轴上一点，当△ACP是等腰三角形时，写出点P的坐标．（直接写出答案，不需要解答过程）
考点二 反比例函数与平行四边形的综合应用
例题：（2022·河南南阳·八年级期中）已知，如图，在平面直角坐标系中，点A（2，0），C（-1，2）是平行四边形OABC的两个顶点，反比例函数的图像经过点B．
(1)求出反比例函数的表达式；
(2)将平行四边形OABC沿着x轴翻折，点C落在点D处，判断点D是否在反比例函数的图像上，并说明理由；
(3)在x轴上是否存在一点P，使是以OC为腰的等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
【变式训练】
1．（2022·福建泉州·八年级期中）如图，点D是平行四边形内一点，轴，轴，且，，，若反比例函数的图象经过A、D两点，则k的值是______．
2．（2021·河北保定·九年级期末）如图，平行四边形OABC的边OC在y轴上，对角线AC，OB交于点D，函数的图象经过点和点D．
(1)求k值和点D的坐标；
(2)求平行四边形OABC的周长．
3．（2022·河南南阳·八年级期中）如图，已知平行四边形ABCD的顶点A、C在反比例函数的图象上，顶点B、D在轴上． 已知点、．
(1)直接写出点C、D的坐标；
(2)求反比例函数的解析式；
(3)求平行四边形ABCD的对角线AC、BD的长；
(4)求平行四边形ABCD的面积S．
4．（2022·江苏·泰州中学附属初中八年级期末）如图在平面直角坐标系中，已知直线y＝﹣x+2及双曲线y＝（k＞0，x＞0）．直线交y轴于A点，x轴于B点，C、D为双曲线上的两点，它们的横坐标分别为a，a+m（m＞0）．
(1)如图①连接AC、DB、CD，当四边形CABD为平行四边形且a＝2时，求k的值．
(2)如图②过C、D两点分别作轴交直线AB于C'，D'，当CDAB时，
①对于确定的k值，求证：a（a+m）的值也为定值．
②若k＝6，且满足m＝a﹣4+，求d的最大值．
5．（2021·湖南永州·九年级期中）如图1，O为坐标原点，点B在x轴的正半轴上，四边形OACB是平行四边形，点A的坐标为，反比例函数在第一象限内的图像经过点A，与BC相交于F．
(1)若，求反比例函数的关系式．
(2)若点F为BC的中点，且△AOF的面积S=9，求OA的长和点C的坐标；
(3)在（2）的条件下，过点F作EF∥OB，交OA于点E（如图2），点P为直线EF上的一个动点，连接PA，PO．是否存在这样的点P、使以P、O、A为顶点的三角形是以OA为斜边的直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．
考点三 反比例函数与矩形的综合应用
例题：（2022·江苏省锡山高级中学实验学校八年级期中）如图1，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点B在反比例函数y＝（k＞0）的第一象限内的图像上，OA＝6，OC＝4，动点P在y轴的右侧，且满足S△PCO＝S矩形OABC．
(1)若点P在这个反比例函数的图像上，求点P的坐标；
(2)若点Q是平面内一点，使得以B、C、P、Q为顶点的四边形是菱形，请你直接写出满足条件的所有点Q的坐标．
【变式训练】
1．（2022·河南南阳·八年级期末）如图，在平面直角坐标系中，反比例函数的图象和矩形ABCD在第一象限，AD平行于x轴，且，，点A的坐标为（2，6）．将矩形向下平移，若矩形的两个顶点恰好同时落在反比例函数的图象上，则矩形的平移距离a的值为（ ）
A．B．C．D．
2．（2022·浙江宁波·八年级期末）如图，矩形OABC被三条直线分割成六个小矩形，若D、E是CO边上的三等分点，反比例函数刚好经过小矩形的顶点F、G，若图中的阴影矩形面积，则反比例系数k的值为__．
3．（2022·四川雅安·九年级专题练习）如图，在矩形中，，，点是边的中点，反比例函数的图像经过点，交于点．
(1)求的值及直线的解析式；
(2)在轴上找一点，使的周长最小，求此时点的坐标；
(3)在（2）的条件下，求的面积．
4．（2022·浙江湖州·八年级期末）矩形OABC的顶点A，C分别在x，y轴的正半轴上，点F是边BC上的一个动点(不与点B，C重合)，过点F的反比例函数的图象与边AB交于点E(8,m)，AB＝4．
(1)如图1，若BE＝3AE．
①求反比例函数的表达式；
②将矩形OABC折叠，使O点与F点重合，折痕分别与x，y轴交于点H，G，求线段OG的长度．
(2)如图2，连接OF，EF，请用含m的关系式表示OAEF的面积，并求OAEF的面积的最大值．
5．（2022·江苏宿迁·八年级期末）如图，矩形的顶点、分别在、轴的正半轴上，点在反比例函数的第一象限内的图像上，，，动点在轴的上方，且满足．
(1)若点在这个反比例函数的图像上，求点的坐标；
(2)连接、，求的最小值；
(3)若点是平面内一点，使得以、、、为顶点的四边形是菱形，则请你直接写出满足条件的所有点的坐标．
考点四 反比例函数与菱形的综合应用
例题：（2022·四川遂宁·八年级期末）如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数的图像上，点D的坐标为（4，3），设AB所在直线解析式为．
(1)求反比例和一次函数解析式．
(2)若将菱形ABCD沿x轴正方向平移m个单位，在平移中若反比例函数图像与菱形的边AD始终有交点，求m的取值范围．
(3)在直线AB上是否存在M、N两点，使以MNOD四点的四边形构成矩形？若不存在，请说明理由，若存在直接求出M、N（点M在点N的上方）两点的坐标．
【变式训练】
1．（2022·江苏·苏州市胥江实验中学校八年级期中）图，在平面直角坐标系中，边长为4的菱形顶点与原点重合，点在轴的正半轴上，点在函数的图象上，________．
2．（2022·江苏南京·二模）如图，菱形ABCD的边BC在x轴上，顶点A，D分别在函数，的图像上．若，则A的坐标为______．
3．（2022·贵州安顺·中考真题）如图，在平面直角坐标系中，菱形的顶点在轴上，，两点的坐标分别为，，直线：与反比例函数的图象交于，两点．
(1)求该反比例函数的解析式及的值；
(2)判断点是否在该反比例函数的图象上，并说明理由．
4．（2022·广东·九年级专题练习）如图，一次函数的图象与反比例函数的图象相交于、两点，点在轴负半轴上，点，连接、、、，四边形为菱形．
（1）求一次函数与反比例函数的解析式；
（2）设点是直线上一动点，且，求点的坐标．
5．（2021·山东济南·一模）如图，在平面直角坐标系中，菱形的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数的图象上，点D的坐标为．
（1）求k的值．
（2）若将菱形沿x轴正方向平移m个单位，
①当菱形的顶点B落在反比例函数的图象上，求m的值；
②在平移中，若反比例函数图象与菱形的边始终有交点，求m的取值范围．
考点五 反比例函数与正方形的综合应用
例题：（2022·江苏淮安·八年级期末）如图，A、B分别是轴正半轴上和轴正半轴上的点，以AB为边在第一象限内作正方形ABCD，反比例函数的图象经过点C．
(1)若点C坐标为（2，3），则的值为______；
(2)若A、B两点坐标分别A（2，0），B（0，2）；
① 则的值为______；
② 此时点D______（填“在”、“ 不在”或者“不一定在”）该反比例函数的图象上；
(3)若C、D两点都在函数的图象上，直接写出点C的坐标为______．
【变式训练】
1．（2022·黑龙江牡丹江·九年级期末）如图，正方形ABCD的边长为3，AD边在x轴负半轴上，反比例函数y=（x＜0）的图像经过点B和CD边中点E，则k的值为______．
2．（2021·江苏·南通市八一中学九年级阶段练习）如图，直线y＝﹣2x+4与x轴，y轴分别相交于点A、B，四边形ABCD是正方形，双曲线在第一象限经过点D，将正方形向下平移m个单位后，点C刚好落在双曲线上，则m＝________________．
3．（2022·福建泉州·八年级期末）如图，正方形ABCD的顶点A在x轴的负半轴上，顶点B在y轴的正半轴上，顶点C、D都在反比例函数图象上，则点C的坐标是______．
4．（2022·广东·佛山市南海区桂城街道映月中学九年级阶段练习）如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为（0，4），点A在x轴正半轴上，点D、E分别在边AB、OA上，且AD＝3BD，AE＝3OE．一次函数y＝kx+b的图象经过点D和点E，反比例函数y＝（x＞0）的图象经过点D，与BC的交点为点F．
(1)求反比例函数和一次函数的解析式；
(2)若点P在直线DE上，且使△OPE的面积与四边形OEFC的面积相等，求点P的坐标．
5．（2022·江苏·八年级专题练习）如图（1），正方形ABCD顶点A、B在函数y＝（k＞0）的图象上，点C、D分别在x轴、y轴的正半轴上，当k的值改变时，正方形ABCD的大小也随之改变．
（1）若点A的横坐标为5，求点D的纵坐标；
（2）如图（2），当k＝8时，分别求出正方形A′B'C′D′的顶点A′、B′两点的坐标．
6．（2022·江西·石城县教育局教研室二模）正方形ABCD的边长为4，AC，BD交于点E．在点A处建立平面直角坐标系如图所示．
（1）如图（1），双曲线y＝过点E，完成填空：点C的坐标是 ，点E的坐标是 ，双曲线的解析式是 ；
（2）如图（2），双曲线y＝与BC，CD分别交于点M，N．求证：；
（3）如图（3），将正方形ABCD向右平移m（m＞0）个单位长度，使过点E的双曲线y＝与AB交于点P．当AEP为等腰三角形时，求m的值．
专题03 反比例函数与几何图形的综合应用
考点一 反比例函数与三角形的综合应用 考点二 反比例函数与平行四边形的综合应用
考点三 反比例函数与矩形的综合应用 考点四 反比例函数与菱形的综合应用
考点五 反比例函数与正方形的综合应用
考点一 反比例函数与三角形的综合应用
例题：（2022·贵州黔东南·中考真题）如图，在平面直角坐标系中，等腰直角三角形的斜边轴于点，直角顶点在轴上，双曲线经过边的中点，若，则______．
【答案】
【分析】根据是等腰直角三角形，轴，得到是等腰直角三角形，再根据求出 A点，C点坐标，根据中点公式求出D点坐标，将D点坐标代入反比例函数解析式即可求得k．
【详解】∵是等腰直角三角形，轴．
∴；．
∴是等腰直角三角形．
∴．
故：，．
．
将D点坐标代入反比例函数解析式．
．
故答案为：．
【点睛】本题考查平面几何与坐标系综合，反比例函数解析式；本体解题关键是得到是等腰直角三角形，用中点公式算出D点坐标．
【变式训练】
1．（2022·山东东营·中考真题）如图，是等腰直角三角形，直角顶点与坐标原点重合，若点B在反比例函数的图象上，则经过点A的反比例函数表达式为____________．
【答案】
【分析】如图所示，过点A作AC⊥x轴于C，过点B作BD⊥x轴于D，证明△ACO≌△ODB得到AC=OD，OC=BD，设点B的坐标为（a，b），则点A的坐标为（-b，a），再由点B在反比例函数，推出，由此即可得到答案．
【详解】解：如图所示，过点A作AC⊥x轴于C，过点B作BD⊥x轴于D，则∠ACO=∠ODB=90°，
由题意得OA=OB，∠AOB=90°，
∴∠CAO+∠COA=∠AOC+∠BOD=90°，
∴∠CAO=∠DOB，
∴△ACO≌△ODB（AAS），
∴AC=OD，OC=BD，
设点B的坐标为（a，b），则AC=OD=a，OC=BD=b，
∴点A的坐标为（-b，a），
∵点B在反比例函数，
∴，
∴，
∴，
∴经过点A的反比例函数表达式为，
故答案为：．
【点睛】本题主要考查了反比例函数与几何综合，全等三角形的性质与判定，熟知相关知识是解题的关键．
2．（2022·江苏·淮安市淮安区教师发展中心学科研训处模拟预测）如图，把一个等腰直角三角形ACB放在平面直角坐标系中，∠ACB＝90°，点C(﹣2,0)，点B在反比例函数的图象上，且y轴平分∠BAC，则k的值是________．
【答案】
【分析】过点B作BD⊥x轴于D，在OA上截取OE=OC，连接CE，由等腰直角三角形的性质可求∠CEO=45°，CE=2，由角平分线的性质和外角的性质可得∠ECA=∠OAC=22.5°，可证CE=AE=2，由“AAS”可证△OAC≌△DCB，可得AO=CD=2+2，OC=BD=2，可得点B坐标，即可求解．
【详解】解：如图，过点B作BD⊥x轴于D，在OA上截取OE=OC，连接CE，
∵点C(-2,0)，
∴CO=2，
∴CO=EO=2，
∴∠CEO=45°，CE=2，
∵△BAC为等腰直角三角形，且∠ACB=90°，
∴BC=AC，∠OCA+∠DCB=90°，∠CAB=45°，
∵∠OCA+∠OAC=90°，
∴∠OAC=∠BCD，
在△OAC和△DCB中
，
∴△OAC≌△DCB(AAS)，
∴AO=CD，OC=BD=2，
∵y轴平分∠BAC，
∴∠CAO=22.5°，
∵∠CEO=∠CEA+∠OAC=45°，
∴∠ECA=∠OAC=22.5°，
∴CE=AE=2，
∴AO=2+2=CD，
∴DO=2，
∴点B坐标为(2,-2)，
∵点B在反比例函数y=的图象上，
∴k=(-2)×2=-4，
故答案为：-4．
【点睛】本题考查了反比例函数图象上点的坐标性质以及全等三角形的判定与性质，求得B的坐标是解题关键．
3．（2022·陕西省西安高新逸翠园学校模拟预测）如图，平面直角坐标系中，△OAB和△BCD都是等腰直角三角形，且∠A＝∠C＝90°，点B、D都在x轴上，点A、C都在反比例函数y＝（x＞0）的图象上，则点C的横坐标为________．
【答案】##
【分析】过点A作AE⊥x轴于点E，过点C作AF⊥x轴于点F，设OE=m，则点A（m，m），点B（2m，0），再利用点A在反比例函数y＝（x＞0）的图象上，求出m，点B的坐标；又设BF=n，，则点C（2m+n，n），再利用点C在反比例函数y＝（x＞0）的图象，求出n，点C的坐标．
【详解】解：如图，过点A作AE⊥x轴于点E，过点C作AF⊥x轴于点F，
∵△OAB是等腰直角三角形，
∴OE=AE=BE，
设OE=m，则点A（m，m），点B（2m，0），
∵点A在反比例函数y＝（x＞0）的图象上，
∴，
解得：(舍去) ，
∴点B（2，0），
同理∵△BCD是等腰直角三角形，
∴BF=CF，
设BF=n，则点C（2+n，n）．
∵点C在反比例函数y＝（x＞0）的图象上，
∴，
解得：(舍去)，
∴．
故答案为：．
【点睛】本题考查反比例函数与几何综合，等腰直角三角形的性质，灵活运用等腰直角三角形的性质是解题的关键．
4．（2022·贵州铜仁·九年级期末）如图1，点A（0，8）、点B（2，a）在直线y＝﹣2x＋b上，反比例函数y＝（x＞0）的图象经过点B．
(1)求a和k的值；
(2)将线段AB向右平移m个单位长度（m＞0），得到对应线段CD，连接AC、BD．
①如图2，当m＝3时，过D作DF⊥x轴于点F，交反比例函数图象于点E，求的值；
②在线段AB运动过程中，连接BC，若△BCD是以BC为腰的等腰三角形，求所有满足条件的m的值．
【答案】(1)a＝4，k＝8
(2)①；②4或5
【分析】（1）先将点A坐标代入直线AB的解析式中，求出a，进而求出点B坐标，再将点B坐标代入反比例函数解析式中即可得出结论；
（2）①先确定出点D(5，4)，进而求出点E坐标，进而求出DE，EF，即可得出结论；
②先表示出点C，D坐标，再分两种情况：Ⅰ、当BC=CD时，判断出点B在AC的垂直平分线上，即可得出结论；
Ⅱ、当BC=BD时，先表示出BC，用BC=BD建立方程求解即可得出结论．
（1）
解：∵点A(0，8)在直线y＝﹣2x＋b上，
∴﹣2×0＋b＝8，
∴b＝8，
∴直线AB的解析式为y＝﹣2x＋8，
将点B（2，a）代入直线AB的解析式y＝﹣2x＋8中，得﹣2×2＋8＝a，
∴a＝4，
∴B(2，4)，
将B(2，4)代入反比例函数解析式y＝(x＞0)中，得k＝xy＝2×4＝8；
（2）
解：①由（1）知，B(2，4)，k＝8，
∴反比例函数解析式为y＝，
当m＝3时，
∴将线段AB向右平移3个单位长度，得到对应线段CD，
∴D(2＋3，4)，
即：D(5，4)，
∵DF⊥x轴于点F，交反比例函数y＝的图象于点E，
∴E(5，)，
∴DE＝4﹣＝，EF＝，
∴＝＝；
②如图，∵将线段AB向右平移m个单位长度(m＞0)，得到对应线段CD，
∴CD＝AB，AC＝BD＝m，
∵A(0，8)，B(2，4)，
∴C(m，8)，D(m＋2，4)，
∵△BCD是以BC为腰的等腰三角形，
∴Ⅰ、当BC＝CD时，
∴BC＝AB，
∴点B在线段AC的垂直平分线上，
∴m＝2×2＝4，
Ⅱ、当BC＝BD时，
∵B(2，4)，C(m，8)，
∴BC＝，
∴＝m，
∴m＝5，
即：△BCD是以BC为腰的等腰三角形，满足条件的m的值为4或5．
【点睛】此题是反比例函数综合题，主要考查了待定系数法，平移的性质，等腰三角形的性质，线段的垂直平分线的判定和性质，用方程的思想解决问题是解本题的关键．
5．（2022·四川遂宁·八年级期末）如图（1），在平面直角坐标系中，将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，点C坐标为（﹣1，0），点A的坐标为（0，2），一次函数y＝kx+b的图象经过点B，C，反比例函数图象也经过点B．
(1)求反比例函数的关系式；
(2)如图（2），M是线段AB上一点，连接OM交AC于点N，△AMN与△CON的面积相等，求出点M的坐标．
(3)若P是y轴上一点，当△ACP是等腰三角形时，写出点P的坐标．（直接写出答案，不需要解答过程）
【答案】(1)
(2)
(3)或或（0，-2）或
【分析】（1）过点B作BF⊥x轴于点F，证明△BFC≌△COA，可得CF＝OA＝2，BF＝OC＝1，可求出点B的坐标，即可求解；
（2）根据，可得，从而得到直线轴 ，进而得到点M横坐标为-1 ，再求出直线AB解析式，即可求解；
（3）根据等腰三角形的性质，分三种情况讨论，即可求解．
（1）
解：∵点C坐标为（﹣1，0），点A的坐标为（0，2），
∴OC=1，OA=2，
过点B作BF⊥x轴于点F，
∵∠BCA＝90°，
∴∠BCF+∠ACO＝90°．
又∵∠CAO+∠ACO＝90°，
∴∠BCF＝∠CAO，
∵∠BFC＝∠COA＝90°，BC＝AC．
∴△BFC≌△COA（AAS），
∴CF＝OA＝2，BF＝OC＝1，
∴点B的坐标为（﹣3，1），
将点B的坐标代入反比例函数解析式可得：，解得：k＝﹣3，
∴反比例函数解析式为；
（2）
解： 如图，
∵，
∴
∴，
∴点M到y轴的距离等于点C到y轴的距离，
∴直线轴 ，
∴点M横坐标为-1 ，
设直线AB解析式为
又∵B(-3，1) A(0，2)
∴，解得：，
∴直线AB解析式为，
∴当x=-1时，，
∴M坐标为；
（3）
解：∵OC=1，OA=2，
∴，
如图，
若AP=AC，
当点P在y轴正半轴时，，
∴点；
当点P在y轴负半轴时，，
∴点；
若CP=AC，
∵OC⊥y轴，
∴，
∴点；
若AP=CP，设点，
∴，
在中，由勾股定理得：
，解得：，
∴点；
综上所述，点P坐标为或或（0，-2）或．
【点睛】本题主要考查了反比例函数和一次函数的综合，等腰三角形的性质，勾股定理，全等三角形的判定和性质，利用数形结合思想解答是解题的关键．
考点二 反比例函数与平行四边形的综合应用
例题：（2022·河南南阳·八年级期中）已知，如图，在平面直角坐标系中，点A（2，0），C（-1，2）是平行四边形OABC的两个顶点，反比例函数的图像经过点B．
(1)求出反比例函数的表达式；
(2)将平行四边形OABC沿着x轴翻折，点C落在点D处，判断点D是否在反比例函数的图像上，并说明理由；
(3)在x轴上是否存在一点P，使是以OC为腰的等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由．
【答案】(1)
(2)点D在反比例函数的图像上，理由见解析
(3)（，0）或（，0）或P（-2，0）
【分析】（1）过C作CE⊥x轴于E，过B作BF⊥x轴于F，证明△CEO≌△BFA得到OE=AF，CE=BF，求出点B坐标即可求得m值；
（2）根据翻折性质求得点D坐标，将点D坐标代入反比例函数解析式中判断即可；
（3）先求出OC，分OP=OC、CP=OC两种情况求解即可．
（1）
解：过C作CE⊥x轴于E，过B作BF⊥x轴于F，则∠CEO=∠BFA=90°，
∵四边形OABC是平行四边形，
∴OCAB，OC=AB，
∴∠COE=∠BAF，
∴△CEO≌△BFA（AAS），
∴OE=AF，CE=BF，
∵A（2，0），C（-1，2），
∴AF=OE=1，BF=CE=2，OA=2，
∴OF=OA-AF=1，则点B坐标为（1，2），
将点B（1，2）代入，得：m=2，
∴反比例函数的表达式为；
（2）
解：点D在反比例函数的图像上，理由为：
根据翻折性质得点D坐标为（-1，-2），
∵当x=-1时，=-2，
∴点D在反比例函数的图像上；
（3）
解：存在，如图，
∴，
当OP=OC时，OP=，则P1（，0）或P2（，0），
当CP=OC时，OP3=2OE=2，则点P3（-2，0），
综上，满足条件的点P坐标为（，0）或（，0）或P（-2，0）．
【点睛】本题考查反比例函数与几何图形的综合，涉及平行四边形的性质、反比例函数的性质、待定系数法求函数解析式、全等三角形的判定与性质、翻折性质、等腰三角形的性质、坐标与图形等知识，熟练掌握相关知识的联系与运用，利用数形结合和分类讨论思想求解是解题的关键．
【变式训练】
1．（2022·福建泉州·八年级期中）如图，点D是平行四边形内一点，轴，轴，且，，，若反比例函数的图象经过A、D两点，则k的值是______．
【答案】12
【分析】作AM⊥y轴于M，延长BD，交AM于E，设BC与y轴的交点为N，证明△AOM≌△CBD（AAS），得出OM=BD=2，根据△ABD的面积求出AE=4，设D点横坐标为m，表示出D（m，6），则A点坐标为（m+4，2），据反比例函数的定义得出关于m的方程，即可求出m和k的值．
【详解】解：作AM⊥y轴于M，延长BD，交AM于E，设BC与y轴的交点为N，如下图所示：
∵四边形OABC是平行四边形，
∴OABC，OA=BC，
∴∠AOM=∠CNM，
∵BDy轴，
∴∠CBD=∠CNM，
∴∠AOM=∠CBD，
∵CD与x轴平行，BD与y轴平行，
∴∠CDB=90°，BE⊥AM，
∴∠CDB=∠AMO，
∴△AOM≌△CBD（AAS），
∴OM=BD=2，
∵S△ABD=BD•AE=4，
∴AE=4，
∵∠ADB=135°，
∴∠EDA=45°，
∴△ADE是等腰直角三角形，
∴DE=AE=4，
∴D点纵坐标为6，
设D点横坐标为m，
∴D点坐标为（m，6），
A点坐标为（m+4，2），
∵反比例函数图象经过A、D两点，
∴k=6m=（m+4）×2，
解得m=2，k=12．
故答案为：12．
【点睛】本题考查了反比例函数图象上点的坐标特征，反比例函数与平行四边形的综合，表示出A、D的坐标是解决本题的关键．
2．（2021·河北保定·九年级期末）如图，平行四边形OABC的边OC在y轴上，对角线AC，OB交于点D，函数的图象经过点和点D．
(1)求k值和点D的坐标；
(2)求平行四边形OABC的周长．
【答案】(1)，D(6，10)；
(2)
【分析】（1）将A点坐标代入反比例函数解析式，即可求出k的值，从而得到反比例函数解析式为．根据题意可知，由平行四边形的性质可知，代入反比例函数解析式即可求出，即得出D点坐标；
（2）由A点坐标可求出OA的长，再根据平行四边形的性质可得，即可求出OC的长，最后根据平行四边形的周长公式计算即可．
（1）
∵函数的图象经过点，
∴，解得：．
∴反比例函数解析式为．
∵平行四边形OABC的边OC在y轴上，且对角线AC，OB交于点D，
∴，
∴．
∵函数的图象经过点D，
∴，
∴D(6，10)；
（2）
∵，
∴．
∵，，且
∴．
∴，
∴．
【点睛】本题考查反比例函数与平行四边形的综合．利用数形结合的思想是解题关键．
3．（2022·河南南阳·八年级期中）如图，已知平行四边形ABCD的顶点A、C在反比例函数的图象上，顶点B、D在轴上． 已知点、．
(1)直接写出点C、D的坐标；
(2)求反比例函数的解析式；
(3)求平行四边形ABCD的对角线AC、BD的长；
(4)求平行四边形ABCD的面积S．
【答案】(1)C(3，-2)；D（5，0）
(2)
(3)；
(4)
【分析】（1）由题意，点A、C，点B、D关于原点对称，即可得出答案；
（2）直接将点代入反比例函数，即可求出解析式；
（3）直接根据B、D的坐标得到BD的长，过点A作AE⊥x轴于E，有勾股定理可求出OA的长，即可得出AC的长；
（4）由，即可求解．
（1）
解：由题意点A、C，点B、D关于原点对称，且、，
∴C(3，-2)；D（5，0）．
（2）
∵反比例函数图象经过点（-3，2），
∴
反比例函数的解析式为．
（3）
；
过点A作AE⊥x轴于E，在Rt△AEO中，
，
∴．
（4）
．
【点睛】本题考查反比例函数，平行四边形，熟练运用反比例函数的对称性是解题的关键．
4．（2022·江苏·泰州中学附属初中八年级期末）如图在平面直角坐标系中，已知直线y＝﹣x+2及双曲线y＝（k＞0，x＞0）．直线交y轴于A点，x轴于B点，C、D为双曲线上的两点，它们的横坐标分别为a，a+m（m＞0）．
(1)如图①连接AC、DB、CD，当四边形CABD为平行四边形且a＝2时，求k的值．
(2)如图②过C、D两点分别作轴交直线AB于C'，D'，当CDAB时，
①对于确定的k值，求证：a（a+m）的值也为定值．
②若k＝6，且满足m＝a﹣4+，求d的最大值．
【答案】(1)k＝6
(2)①见解析；②当a＝1时，d的最大值为14
【分析】（1）先求出点，点坐标，由平行四边形的性质列出方程组，即可求解；
（2）①先证四边形是平行四边形，可得，列出方程可求解；
②将和代入，再利用二次函数的性质可求解．
（1）
解：直线交轴于点，交轴于点，
点，点，
、为双曲线上的两点，
点，点，
四边形为平行四边形，
与互相平分，
，，
解得：，；
（2）
证明：∵轴，CDAB，
四边形是平行四边形，
，
、为双曲线上的两点，
点，点，
∵轴，
点的横坐标为，点的横坐标为，
点，点，
，
，
当为定值时，为定值；
②解：，
，
，
，
，
，
当时，的最大值为14．
【点睛】本题是反比例函数综合题，考查了反比例函数的性质，平行四边形的性质，二次函数的性质等知识，利用参数表示点的坐标是解题的关键．
5．（2021·湖南永州·九年级期中）如图1，O为坐标原点，点B在x轴的正半轴上，四边形OACB是平行四边形，点A的坐标为，反比例函数在第一象限内的图像经过点A，与BC相交于F．
(1)若，求反比例函数的关系式．
(2)若点F为BC的中点，且△AOF的面积S=9，求OA的长和点C的坐标；
(3)在（2）的条件下，过点F作EF∥OB，交OA于点E（如图2），点P为直线EF上的一个动点，连接PA，PO．是否存在这样的点P、使以P、O、A为顶点的三角形是以OA为斜边的直角三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由．
【答案】(1)
(2)OA＝5，
(3)存在，P（4，2） 或P（-1，2）
【分析】（1）把点A坐标代入解析式，即可求解；
（2）根据反比函数的比例系数的几何意义可得，从而得到，，进而得到点F的坐标为（6a，2a），可得到，求出a，即可求解；
（3）先证得四边形OBFE为平行四边形，可求出点E，然后分两种情况讨论，即可求解．
（1）解∶∵点A的坐标为，，∴点A的坐标为，把代入得：k=48，∴反比例函数的关系式为；
（2）解：分别过点A，F，C作x轴的垂线交x轴于点D，E，G，AD交OF于点H．∵点A，F在反比例函数图像上，∴又，，∵△AOF的面积S=9，四边形OACB是平行四边形，，，∵点A的坐标为，AC∥x轴，∴点C的纵坐标为4a，点F为BC的中点，k=12a2，∴点F的纵坐标为2a，∴点F的横坐标为， 点F的坐标为（6a，2a），，解得a＝1，∴点A（3，4），F（6，2），OD＝3 AD＝4，OA＝5，∵，∴AC=OB＝ ，∴点，即；
（3）解：存在，根据题意得：∠APO=90°，∵四边形OACB为平行四边形，∴OE∥BF，OA=BC，∵EF∥OB，∴四边形OBFE为平行四边形，∴OE=BF，∵BF=CF，∴AE=OE=，∴PE=，由（2）得：点A（3，4），∴点E，∴ON=，EN=2，如图，当点P在线段OA的右侧上时，过点P作PM⊥x轴于点M，过点E作EN⊥x轴于点N，∵EN⊥x轴，PM⊥x轴，∴EN∥PM，∴四边形ENMP为平行四边形，∴PE=MN=，PM=EN=2，∴OM=4，∴点P（4，2）；如图，当点P在线段OA的作侧上时，过点P作PT⊥x轴于点T，过点E作ES⊥x轴于点S，同理：四边形PEST为平行四边形，∴PT=ES=2，TS=PE=，OS=，∴OT=1，∴点P（-1，2）；综上所述，点P的坐标为（4，2）或（-1，2）．
【点睛】本题主要考查了反比例函数的图像和性质，平行四边形的判定和性质，直角三角形的性质，熟练掌握反比例函数的图像和性质，平行四边形的判定和性质，利用数形结合思想解答是解题的关键．
考点三 反比例函数与矩形的综合应用
例题：（2022·江苏省锡山高级中学实验学校八年级期中）如图1，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点B在反比例函数y＝（k＞0）的第一象限内的图像上，OA＝6，OC＝4，动点P在y轴的右侧，且满足S△PCO＝S矩形OABC．
(1)若点P在这个反比例函数的图像上，求点P的坐标；
(2)若点Q是平面内一点，使得以B、C、P、Q为顶点的四边形是菱形，请你直接写出满足条件的所有点Q的坐标．
【答案】(1)点P的坐标为
(2)点Q的坐标为（11，）或（11，）或（－1，）或（－1，）
【分析】（1）首先根据点B坐标，确定反比例函数的解析式，设点P的横坐标为m（m>0），根据S△PCO＝S矩形OABC构建方程，即可求解；
（2）分两种情形：当四边形CBQP是菱形时，当四边形CBPQ是菱形时，分别求解，即可解决问题．
（1）
解：∵四边形OABC是矩形，OA＝6，OC＝4，
∴点B的坐标为（6，4），
∵点B在反比例函数y＝（k＞0）的第一象限内的图像上，
∴，
∴反比例函数的解析式为y＝，
设点P的横坐标为m（m>0），
∵S△PCO＝S矩形OABC，
∴，即，
∵点P在这个反比例函数的图像上，
∴点P的纵坐标为，
∴点P的坐标为；
（2）
解：由（1）可知点P的横坐标为5，
∴设点Q的坐标为（a，b），点P的坐标为（5，c），
分两种情况：
当四边形CBQP是菱形时，如图2，
由菱形和矩形的性质可知，PC=BC=OA＝6，
∴，即，
解得，
∴点P的坐标为（5，）或（5，），
∵，
∴点Q的纵坐标为，
∵PQ=PC= 6，
∴，
解得，
∴点Q的坐标为（11，）或（11，）；
②当四边形CBPQ是菱形时，如图3，
由菱形和矩形的性质可知，
PB=BC=OA＝6，
∴，即，
解得，
∴点P的坐标为（5，）或（5，），
∵，
∴点Q的纵坐标为，
∵PQ=BC= 6，
∴，
解得，
∴点Q的坐标为（－1，）或（－1，）；
综上，点Q的坐标为（11，）或（11，）或（－1，）或（－1，）．
【点睛】本题考查反比例函数综合问题、矩形的性质、菱形的判定和性质、三角形的面积等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想解决问题．
【变式训练】
1．（2022·河南南阳·八年级期末）如图，在平面直角坐标系中，反比例函数的图象和矩形ABCD在第一象限，AD平行于x轴，且，，点A的坐标为（2，6）．将矩形向下平移，若矩形的两个顶点恰好同时落在反比例函数的图象上，则矩形的平移距离a的值为（ ）
A．B．C．D．
【答案】B
【分析】如图，根据矩形的性质以及平移的性质，得到平移后A与C在反比例函数图象上，从而根据反比例函数图象上的点的坐标特征解决此题．
【详解】解：如图．
由题意知，矩形平移到图示的位置时，矩形的两个顶点恰好同时落在反比例函数的图象．
∵AB=2，AD=4，平移前点A的坐标为（2，6），
∴平移后A坐标为（2，6-a），平移后点C的坐标为C（6，4-a）．
∴2（6-a）=6（4-a）．
∴a=3．
故选：B．
【点睛】本题主要考查反比例函数图象上的点的坐标特征、矩形的性质、平移，熟练掌握反比例函数图象上的点的坐标特征、矩形的性质、平移的性质是解决本题的关键．
2．（2022·浙江宁波·八年级期末）如图，矩形OABC被三条直线分割成六个小矩形，若D、E是CO边上的三等分点，反比例函数刚好经过小矩形的顶点F、G，若图中的阴影矩形面积，则反比例系数k的值为__．
【答案】10
【分析】根据题意求得，进而即可根据反比例函数系数k的几何意义求得k的值．
【详解】是CO边上的三等分点，
，
，
反比例函数刚好经过小矩形的顶点，
，
故答案为：10．
【点睛】本题考查反比例函数系数k的几何意义，矩形的面积，求得矩形OAGD的面积是关键．
3．（2022·四川雅安·九年级专题练习）如图，在矩形中，，，点是边的中点，反比例函数的图像经过点，交于点．
(1)求的值及直线的解析式；
(2)在轴上找一点，使的周长最小，求此时点的坐标；
(3)在（2）的条件下，求的面积．
【答案】(1)，直线解析式为
(2)的周长最小时，
(3)
【分析】（1）先求出D点坐标，然后再代入反比例函数解析式可求得k；然后再确定点E得坐标，再通过待定系数法即可解答；
（2）先求出关于轴对称点为，连接D′E交x轴于点P，此时△PDE周长最小，再运用待定系数法求得直线的解析式，直线与x轴的交点即为P点坐标；
（3）先求出直线DE与x轴交点Q的坐标，再求出PE的长，然后结合点D、点E的坐标可求得、,最后根据求解即可．
（1）
解：∵，，
∴．
又∵点是边的中点，
∴，
∴
反比例函数解析式为，
∵为上一点，得．
∴，
∴，
设直线解析式为得：
，解得，
∴直线解析式为．
（2）
解：关于轴对称点为，
连接D′E交x轴于点P，此时△PDE周长最小，
设直线解析式为得
，解得，
∴直线解析式为
∴直线与轴交点为，
∴的周长最小时，．
（3）
解：直线解析式为，设其与轴的交点为，
当y2=0，可得x=6
∴的坐标为，
∵，
∴，
又∵，，
∴，
∴ ，
∴．
【点睛】本题属于反比例综合题，主要考查了反比例函数解析式、最短路径以及三角形的面积等知识点，掌握数形结合思想成为解答本题的关键．
4．（2022·浙江湖州·八年级期末）矩形OABC的顶点A，C分别在x，y轴的正半轴上，点F是边BC上的一个动点(不与点B，C重合)，过点F的反比例函数的图象与边AB交于点E(8,m)，AB＝4．
(1)如图1，若BE＝3AE．
①求反比例函数的表达式；
②将矩形OABC折叠，使O点与F点重合，折痕分别与x，y轴交于点H，G，求线段OG的长度．
(2)如图2，连接OF，EF，请用含m的关系式表示OAEF的面积，并求OAEF的面积的最大值．
【答案】(1)①y
②
(2)20
【分析】(1 )①首先求出AE的长，从而得出点E的坐标，即可得出k的值；
②利用反比例函数图象上点的坐标的特征求出CF的长，设OG＝x，则CG＝4﹣x，FG＝x，利用勾股定理列方程，从而解决问题；
(2 )利用反比例函数图象上点的坐标的特征求出CF＝2m，再利用矩形面积减去△OCF和△BEF的面积，从而表示出四边形OAEF的面积，再利用配方法求出最大值．
（1）
解：①∵BE＝3AE，AB＝4，
∴AE＝1，BE＝3，
∴E(8，1)，
∴k＝8×1＝8，
∴反比例函数表达式为y；
②当y＝4时，x＝2，
∴F(2,4)，
∴CF＝2，
设OG＝x，则CG＝4﹣x，FG＝x，
由勾股定理得，
，
解得x，
∴OG；
（2）
解：∵点E、F在反比例函数的图象上，
∴CF×4＝8m，
∴CF＝2m，
∴四边形OAEF的面积为8×4
=-+4m+16＝﹣+20，
∵0＜m＜4，
∴当m＝2时，四边形OAEF的面积最大为20．
【点睛】本题考查待系数法求反比例函数解析式，矩形的性质，勾股定理，坐标与图形，二次函数的最值，熟练掌握用待系数法求反比例函数解析式、勾股定理、二次函数的性质是解题的关键．
5．（2022·江苏宿迁·八年级期末）如图，矩形的顶点、分别在、轴的正半轴上，点在反比例函数的第一象限内的图像上，，，动点在轴的上方，且满足．
(1)若点在这个反比例函数的图像上，求点的坐标；
(2)连接、，求的最小值；
(3)若点是平面内一点，使得以、、、为顶点的四边形是菱形，则请你直接写出满足条件的所有点的坐标．
【答案】(1)
(2)
(3)，，或
【分析】（1）由矩形的性质可得出点的坐标，利用反比例函数图像上点的坐标特征可求出的值，进而可得出反比例函数解析式，由可求出点的纵坐标，再利用反比例函数图像上点的坐标特征可求出点的坐标；
（2）作点关于直线的对称点，连接'交直线于点，利用两点之间线段最短可得出此时取得最小值，由点的坐标可求出点的坐标，再利用勾股定理即可求出的最小值；
（3）设点的坐标为，由线段的长及点的纵坐标可得出只能为边，分点在点的上方及点在点的下方两种情况考虑：①当点在点的上方时，由可求出的值，进而可得出点，的坐标，结合可得出点，的坐标；②当点在点的下方时，由可求出的值，进而可得出点，的坐标，结合可得出点，的坐标．综上，此题可得解．
(1)
解：∵四边形是矩形，，，
∴点的坐标为，，
∵点在反比例函数的第一象限内的图像上，
∴，
∴反比例函数的解析式为，
设点的纵坐标为，
∵，
∴，
∴，
当时，，解得：，
∴当点在这个反比例函数的图像上，点的坐标为；
(2)
如图1，由（1）可知，点在直线上，作点关于直线的对称点，连接'交直线于点，
∵点和点关于直线的对称，
∴直线垂直平分，
∴，
∴，
即此时取得最小值，最小值为的长，
∵点的坐标为，
∴点的坐标为，
∵点的坐标为，，
∴．
∴的最小值为．
(3)
∵轴，，点的纵坐标为，
∴不能为对角线，只能为边，
设点的坐标为，
分两种情况考虑，如图2所示：
①当点在点的上方时，由，
∴，
解得：，，
∴点的坐标为，点的坐标为，
又∵，且轴，
∴点的坐标为，点的坐标为；
②当点在点的下方时，由，
∴，
解得：，，
∴点的坐标为，点的坐标为，
又∵，且轴，
∴点的坐标为，点的坐标为．
综上所述：当以、、、为顶点的四边形是菱形时，点的坐标为，，或．
【点睛】本题考查反比例函数综合题、矩形的性质、菱形的判定和性质、三角形的面积、轴对称最短问题，勾股定理等知识．解题的关键是灵活运用所学知识解决问题，学会利用轴对称解决最短问题，学会用分类讨论的方法思考问题．
考点四 反比例函数与菱形的综合应用
例题：（2022·四川遂宁·八年级期末）如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数的图像上，点D的坐标为（4，3），设AB所在直线解析式为．
(1)求反比例和一次函数解析式．
(2)若将菱形ABCD沿x轴正方向平移m个单位，在平移中若反比例函数图像与菱形的边AD始终有交点，求m的取值范围．
(3)在直线AB上是否存在M、N两点，使以MNOD四点的四边形构成矩形？若不存在，请说明理由，若存在直接求出M、N（点M在点N的上方）两点的坐标．
【答案】(1)，
(2)0≤m≤
(3)点N坐标为（，）；点M的坐标为（，）
【分析】（1）延长AD交x轴于F，根据菱形的性质和勾股定理得到A、B的坐标，利用待定系数法求解函数解析式即可；
（2）根据平移性质，只需求得点D平移后落在反比例函数图像上时的坐标即可求解；
（3）延长AD交x轴于F，过点N作NH⊥y轴于H，证明△ONB≌△OFD（AAS）得到S△ONB=S△OFD，求出NH即可求得点N坐标，设M（x，），利用中点坐标公式即可求出点M坐标．
（1）解：延长AD交x轴于F，∵四边形ABCD是菱形，∴OB=OD=AD，AD∥OB，则AF⊥x轴，∵点D坐标为（4，3），∴OF=4，DF=3，∴OD=5，即OB=AD=5，∴A（4，8），B（0，5），∴k=4×8=32，∴反比例函数的解析式为；将A、B坐标代入中，得，解得：，∴一次函数的解析式为；
（2）解：由题意知，将菱形ABCD沿x轴正方向平移m个单位，使得点D落在反比例函数的图像D′处，∵点D平移后的坐标为D′（4+m，3），∴，∴m= ，∴满足条件的m的取值范围为0≤m≤．
（3）解：存在，理由为：如图，延长AD交x轴于F，过点N作NH⊥y轴于H，则∠NHO=∠OFD=90°，由题意，∠ONB=∠NOD=∠HOF=90°，则∠NOB=∠FOD，又∠ONB=∠OFD=90°，OB=OD，∴△ONB≌△OFD（AAS），∴S△ONB=S△OFD，则，∴NH=，∵点N在直线AB上，∴当x=时，，∴点N坐标为（，）；设M（x，），则x+0=+4，解得：x=，，∴点M的坐标为（，）．
【点睛】本题是反比例函数与几何图形的综合题，涉及菱形的性质、矩形的性质、待定系数法求函数解析式、全等三角形的判定与性质、坐标与图形、平移性质等知识，熟练掌握相关知识的联系与运用，添加辅助线，利用数形结合思想求解是解答的关键．
【变式训练】
1．（2022·江苏·苏州市胥江实验中学校八年级期中）图，在平面直角坐标系中，边长为4的菱形顶点与原点重合，点在轴的正半轴上，点在函数的图象上，________．
【答案】
【分析】延长AD交x轴于F，求出DF和OF，即可求出A点的坐标，再代入函数解析式求出k即可
【详解】解：延长AD交x轴于F，
∵四边形ABOD是菱形，
∴AD=OD=4，
∵
∴
∴，
∴，
又，AD∥OB，
∴A点的坐标是（，6），
代入y=得：k=6×=，
故答案为：
【点睛】本题考查了反比例函数图象上点的坐标，用待定系数法求反比例函数的解析式和菱形的性质等知识点，能求出反比例函数的解析式是解此题的关键．
2．（2022·江苏南京·二模）如图，菱形ABCD的边BC在x轴上，顶点A，D分别在函数，的图像上．若，则A的坐标为______．
【答案】
【分析】过点D作DE⊥x轴于点E，设DE=n，则，，即可得出，然后根据菱形的性质及含30°直角三角形的性质可求出n的值，进而问题可求解．
【详解】解：过点D作DE⊥x轴于点E，如图所示：
设DE=n，由四边形ABCD是菱形可知：，
∴点A、D的纵坐标为n，
∵顶点A，D分别在函数，的图像上，
∴，，
∴，
∵，
∴，
∴，即，
解得：，
∴点；
故答案为．
【点睛】本题主要考查反比例函数与几何的综合、含30度直角三角形的性质及菱形的性质，熟练掌握反比例函数与几何的综合、含30度直角三角形的性质及菱形的性质是解题的关键．
3．（2022·贵州安顺·中考真题）如图，在平面直角坐标系中，菱形的顶点在轴上，，两点的坐标分别为，，直线：与反比例函数的图象交于，两点．
(1)求该反比例函数的解析式及的值；
(2)判断点是否在该反比例函数的图象上，并说明理由．
【答案】(1)，
(2)点在该反比例函数的图象上，理由见解答
【分析】（1）因为点在双曲线上，所以代入点坐标即可求出双曲线的函数关系式，又因为点在双曲线上，代入即可求出的值；
（2）先求出点的坐标，判断即可得出结论．
（1）
解：将点代入中，得，
反比例函数的解析式为，
将点代入中，
得；
（2）
解：因为四边形是菱形，，，
，，
，
由（1）知双曲线的解析式为；
，
点在双曲线上．
【点睛】此题是反比例函数综合题，主要考查了待定系数法，菱形的性质，解题的关键是用表示出点的坐标．
4．（2022·广东·九年级专题练习）如图，一次函数的图象与反比例函数的图象相交于、两点，点在轴负半轴上，点，连接、、、，四边形为菱形．
（1）求一次函数与反比例函数的解析式；
（2）设点是直线上一动点，且，求点的坐标．
【答案】（1）一次函数的解析式为，反比例函数的解析式为；（2）或
【分析】（1）由菱形的性质可知、关于轴对称，可求得点坐标，把点坐标分别代入两函数解析式可求得和值；
（2）根据（1）可求得菱形面积，设点坐标为，根据条件可得到关于的方程，可求得点坐标．
【详解】解：（1）如图，连接，交轴于点，
四边形是菱形，
∴AD⊥OC，
，
，，
四边形是菱形，
，，
，
将代入直线，
得：，
解得：，
将代入反比例函数，
得：，
解得：，
一次函数的解析式为，反比例函数的解析式为；
（2），，
，
，
，
设点坐标为，与轴相交于点，
则，
，
，
当在的左侧时，，
，
，，
，
当在的右侧时，，
，
，，
，
综上所述，点的坐标为或．
【点睛】本题为反比例函数的综合应用，主要考查了待定系数法求函数解析式、菱形的性质、三角形的面积及数形结合思想、分类讨论思想等，题目难度不大，但是属于中考常考题，熟练掌握反比例函数图象和性质及待定系数法等相关知识，并能够灵活运用方程思想、数形结合思想和分类讨论思想是解题关键．
5．（2021·山东济南·一模）如图，在平面直角坐标系中，菱形的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数的图象上，点D的坐标为．
（1）求k的值．
（2）若将菱形沿x轴正方向平移m个单位，
①当菱形的顶点B落在反比例函数的图象上，求m的值；
②在平移中，若反比例函数图象与菱形的边始终有交点，求m的取值范围．
【答案】（1）；（2）①，②．
【分析】（1）先由点D的坐标确定出AD，从而求出点A坐标，最后求出；
（2）①由平移的性质确定出的纵坐标，根据解析式求出点的横坐标，即可；②由平移的性质求出点D落在双曲线上的横坐标的值即可求出反比例函数图象与菱形的边AD始终有交点的的取值范围．
【详解】（1）过点D作x轴的垂线，垂足为F，
如图所示：
∵点D的坐标为，
∴，
∴，
∴菱形，
∴，
∴，
∵点A在反比例函数的图象上，
∴，
（2）①将菱形沿x轴正方向平移m个单位，
则平移后，
∵菱形的顶点B落在反比例函数的图象上，
∴，
②如图，
将菱形沿x轴正方向平移m个单位，
使得点D落在函数的图象处，
过点作x轴的垂线，垂足为，
∵，
∴，
∴点的纵坐标为3，
∵落在函数的图象上，
∴，
∴，
∴，
∴，
∴．
【点睛】本题考查了反比例函数，利用待定系数法求函数解析式，菱形的性质和勾股定理，解本题的关键是判断菱形ABCD的边AD始终和双曲线有交点的分界点．
考点五 反比例函数与正方形的综合应用
例题：（2022·江苏淮安·八年级期末）如图，A、B分别是轴正半轴上和轴正半轴上的点，以AB为边在第一象限内作正方形ABCD，反比例函数的图象经过点C．
(1)若点C坐标为（2，3），则的值为______；
(2)若A、B两点坐标分别A（2，0），B（0，2）；
① 则的值为______；
② 此时点D______（填“在”、“ 不在”或者“不一定在”）该反比例函数的图象上；
(3)若C、D两点都在函数的图象上，直接写出点C的坐标为______．
【答案】(1)6
(2)①8，②在；
(3)（1，2）
【分析】（1）运用待定系数法求反比例函数解析式中的的值即可；
（2）①求出C点坐标，运用待定系数法即可；
②由题意可得D点坐标，代入反比例函数解析式，即可得出结论；
（3）根据全等三角形的性质和判定可得C、D点的坐标特点，即可得到点C的坐标
（1）
∵点C坐标为（2，3），反比例函数的图象经过点C，
∴；
（2）
①连接AC，过点C作CE⊥y轴，过点D作CF⊥x轴，如图所示，
∵A、B两点坐标分别A（2，0），B（0，2）
∴OA=OB=2
∵
∴，
在正方形ABCD中，AC为对角线
∴，，
∴C点的横坐标为2
∴
∴
∵反比例函数的图象经过点C
∴
②由上小问可知，反比例函数的解析式为，
∵，
∴
∵CF⊥x轴
∴
∴
∵正方形ABCD，
∴
∴
∴
∴
将代入反比例函数的解析式得，，
∴点D在该反比例函数的图象上
（3）
过点C作CE⊥y轴，过点D作CF⊥x轴，
∵CE⊥y轴，CF⊥x轴，
∴，
∵正方形ABCD，
∴
∴，
∴
在和中，
，
∴≌（AAS）
∴，
同理可得出：≌
∴，
设，
∴，
∵C、D两点都在函数的图象上
∴
∴
∴，
∴
解得：或（不合题意，舍去）
∴点C的坐标：
【点睛】此题主要考查了反比例函数综合以及全等三角形的判定和性质，以及待定系数法求反比例函数解析式，得出C、D点的坐标特点是本题的特点．
【变式训练】
1．（2022·黑龙江牡丹江·九年级期末）如图，正方形ABCD的边长为3，AD边在x轴负半轴上，反比例函数y=（x＜0）的图像经过点B和CD边中点E，则k的值为______．
【答案】-9
【分析】设B(m，3)，把E点的坐标用含m的代数式表示出来．把B、E两点的坐标都代入y=中，先求出m的值，则可求出k的值．
【详解】设B(m，3)，则C((m-3，3)，
∵E点是CD的中点，
∴(m-3， ).
∵B、E都在y=的图像上，
∴，
解得m=-3，
∴B(-3，3)，
∴k=-3×3=-9，
故答案为-9．
【点睛】本题主要考查了用待定系数法求反比例函数的表达式．熟练掌握待定系数法是解题的关键．
2．（2021·江苏·南通市八一中学九年级阶段练习）如图，直线y＝﹣2x+4与x轴，y轴分别相交于点A、B，四边形ABCD是正方形，双曲线在第一象限经过点D，将正方形向下平移m个单位后，点C刚好落在双曲线上，则m＝________________．
【答案】3
【分析】过点C作 轴于点F，过点D作 轴于点E，作 于G，求出D点坐标，代入双曲线，求出双曲线的解析式，再求出C点坐标，根据平移的性质，得到平移后C点的新坐标，代入双曲线即可求出m的值
【详解】如图，过点C作 轴于点F，过点D作 轴于点E，作 于G，
直线y＝﹣2x+4与x轴，y轴分别相交于点A、B，
当 时， ，即
当 时， ，即
四边形ABCD是正方形，




在 和 中，


,

D点坐标为（6，2），
把D点坐标代入双曲线 ，得
则双曲线的解析式为：
同理，

且
四边形DEFG是正方形


C点坐标为（4，6）
当正方形向下平移m个单位后，C点坐标变为（4，6-m），代入双曲线，
得 ，
解得 ．
故答案为：3
【点睛】本题考查函数与几何图形的综合知识，难点在于作辅助线把两者连线起来．
3．（2022·福建泉州·八年级期末）如图，正方形ABCD的顶点A在x轴的负半轴上，顶点B在y轴的正半轴上，顶点C、D都在反比例函数图象上，则点C的坐标是______．
【答案】
【分析】设，作轴于点E，轴于点F，进而得到全等，从而得到用a表示的D的坐标，从而构建方程解出a的值，进而得到C的坐标．
【详解】解：设，作轴于点E，轴于点F，
则CE=-a，，
由四边形ABCD是正方形，
，
，
，
，
同理可得：，
，
，
，
，
，
由点D在反比例函数上，
，
解得：（舍）或，
，
故答案为：
【点睛】本题考查反比例函数图像上的点的坐标特征、正方形的性质、三角形全等的有关知识，属于较难的题．
4．（2022·广东·佛山市南海区桂城街道映月中学九年级阶段练习）如图，在平面直角坐标系中，正方形OABC的顶点O与坐标原点重合，点C的坐标为（0，4），点A在x轴正半轴上，点D、E分别在边AB、OA上，且AD＝3BD，AE＝3OE．一次函数y＝kx+b的图象经过点D和点E，反比例函数y＝（x＞0）的图象经过点D，与BC的交点为点F．
(1)求反比例函数和一次函数的解析式；
(2)若点P在直线DE上，且使△OPE的面积与四边形OEFC的面积相等，求点P的坐标．
【答案】(1)，
(2) 或
【分析】（1）由正方形OABC的顶点C的坐标，确定出边长及四个角为直角，根据AD=3BD，求出AD的长，确定出D点坐标，代入反比例解析式求出m的值，再由AE=3OE，确定出EO的长，即E点坐标，将D与E两点的坐标代入y=kx+b求出k与b的值，即可确定出一次函数的解析式；
（2）把y=4代入反比例解析式求出x的值，确定出F点坐标，得到FC的长，设根据△OPE的面积与四边形OEFC的面积相等，求出x的值，进而得到y的值，确定出P坐标即可．
（1）
解： 正方形OABC的顶点C的坐标为（0，4），
，
，
，AE＝3OE
，
，
把点D的坐标代入 y＝，得，
反比例函数的解析式为，
把点E和点D的坐标代入y＝kx+b，
得，
解得，
一次函数的解析式为；
（2）
把 代入中，得，
，即，
，
设，
则，
△OPE的面积与四边形OEFC的面积相等，
，
，
解得，
当时， ；当时，，
则点P的坐标为 或．
【点睛】此题考查了一次函数与反比例函数的交点问题，涉及的知识有：待定系数法确定一次函数、反比例函数解析式，坐标与图形性质，正方形的性质，以及三角形面积计算，熟练掌握待定系数法是解本题的关键．
5．（2022·江苏·八年级专题练习）如图（1），正方形ABCD顶点A、B在函数y＝（k＞0）的图象上，点C、D分别在x轴、y轴的正半轴上，当k的值改变时，正方形ABCD的大小也随之改变．
（1）若点A的横坐标为5，求点D的纵坐标；
（2）如图（2），当k＝8时，分别求出正方形A′B'C′D′的顶点A′、B′两点的坐标．
【答案】（1）5；（2）A′、B′两点的坐标分别为（2，4），（4，2）．
【分析】（1）过点A作AE⊥y轴于点E，则∠AED＝利用正方形的性质得AD＝DC，∠ADC＝，再根据等角的余角相等得到∠EDA＝∠OCD，利用全等三角形的判定方法可判断出△AED≌△DOC，从而得到OD＝EA＝5，于是确定点D的纵坐标；
（2）作轴于M，轴于点N，设＝a，＝b，同理可得，利用全等的性质得，则，，再根据反比例函数图象上点的坐标特征得到，，解方程组求出a、b，从而得到，两点的坐标．
【详解】解：（1）如图，过点A作AE⊥y轴于点E，则∠AED＝．
∵四边形ABCD为正方形，
∴AD＝DC，∠ADC＝，
∴∠ODC+∠EDA＝．
∵∠ODC+∠OCD＝，
∴∠EDA＝∠OCD，
在△AED和△DOC中
∴△AED≌△DOC（AAS），
∴OD＝EA＝5，
∴点D的纵坐标为5；
（2）作轴于M，轴于点N，
设＝a，＝b，
同理可得
∴，
∴，，
∵点A′、B′在反比例函数y＝的图象上，
∴，，
∴解得a＝b＝2或a＝b＝﹣2（舍去），
∴，两点的坐标分别为（2，4），（4，2）．
【点睛】本题主要考查了反比例函数的图象性质，正方型的性质，全等三角型的判定及性质等知识点，合理做出辅助线是解题的关键．
6．（2022·江西·石城县教育局教研室二模）正方形ABCD的边长为4，AC，BD交于点E．在点A处建立平面直角坐标系如图所示．
（1）如图（1），双曲线y＝过点E，完成填空：点C的坐标是 ，点E的坐标是 ，双曲线的解析式是 ；
（2）如图（2），双曲线y＝与BC，CD分别交于点M，N．求证：；
（3）如图（3），将正方形ABCD向右平移m（m＞0）个单位长度，使过点E的双曲线y＝与AB交于点P．当AEP为等腰三角形时，求m的值．
【答案】（1）(4，4)，(2，2)，；（2）见解析；（3）2或2+2
【分析】（1）根据正方形的边长可确定C点的坐标，再利用正方形的性质得出E点坐标，用待定系数法求出双曲线解析式即可；
（2）设出M点和N点的坐标，根据坐标的性质得出MC＝NC，推出∠CMN＝∠CDB即可得出MN∥BD；
（3）根据E点的坐标求出AE的长，再分三种情况讨论分别求出m的值即可．
【详解】解：（1）∵正方形ABCD的边长为4，AC，BD交于点E，
∴C（4，4），E（2，2），
将E点坐标代入双曲线y＝，
得2＝，
解得k1＝4，
∴双曲线的解析式为y＝，
故答案为：（4，4），（2，2），；
（2）∵双曲线y＝与BC，CD分别交于点M，N，
∴设M（m，4），N（4，n），
∴4m＝4n，
∴m＝n，
∴MC＝NC，
由正方形可知，∠BCD＝90°，
∴∠CMN＝45°，∠CBD＝45°，
∴∠CMN＝∠CBD，
∴MN∥BD；
（3）∵正方形边长为4，
由（1）知E（2，2），
∴AE＝，
①当AP＝AE＝2时，
∵P（m，2），E（m+2，2），点P、E在反比例函数图象上，
∴2m＝2（m+2），
∴m＝2+2；
②当EP＝AE时，点P与点B重合，
∵P（m，4），E（m+2，2），点P、E在反比例函数图象上，
∴4m＝2（m+2），
∴m＝2；
③
当EP＝AP时，
即
当EP＝AP时，点P、E不可能都在反比例函数图象上，故此情况不存在；
综上所述，满足条件的m的值为2或2+2．
【点睛】本题考查了反比例函数与几何图形，正方形的性质，掌握反比例函数的性质是解题的关键．