

2024年新疆自治区北京大附属中学数学九上开学质量跟踪监视模拟试题【含答案】
展开
这是一份2024年新疆自治区北京大附属中学数学九上开学质量跟踪监视模拟试题【含答案】,共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、(4分)如图,矩形纸片中,,把纸片沿直线折叠,点落在处,交于点,若,则的面积为( )
A.B.C.D.
2、(4分)京剧是中国的“国粹”,京剧脸谱是一种具有汉族文化特色的特殊化妆方法由于每个历史人物或某一种类型的人物都有一种大概的谱式,就像唱歌、奏乐都要按照乐谱一样,所以称为“脸谱”如图是京剧华容道中关羽的脸谱图案在下面的四个图案中,可以通过平移图案得到的是
A.B.C.D.
3、(4分)要使分式有意义,则x的取值满足的条件是( )
A.B.C.D.
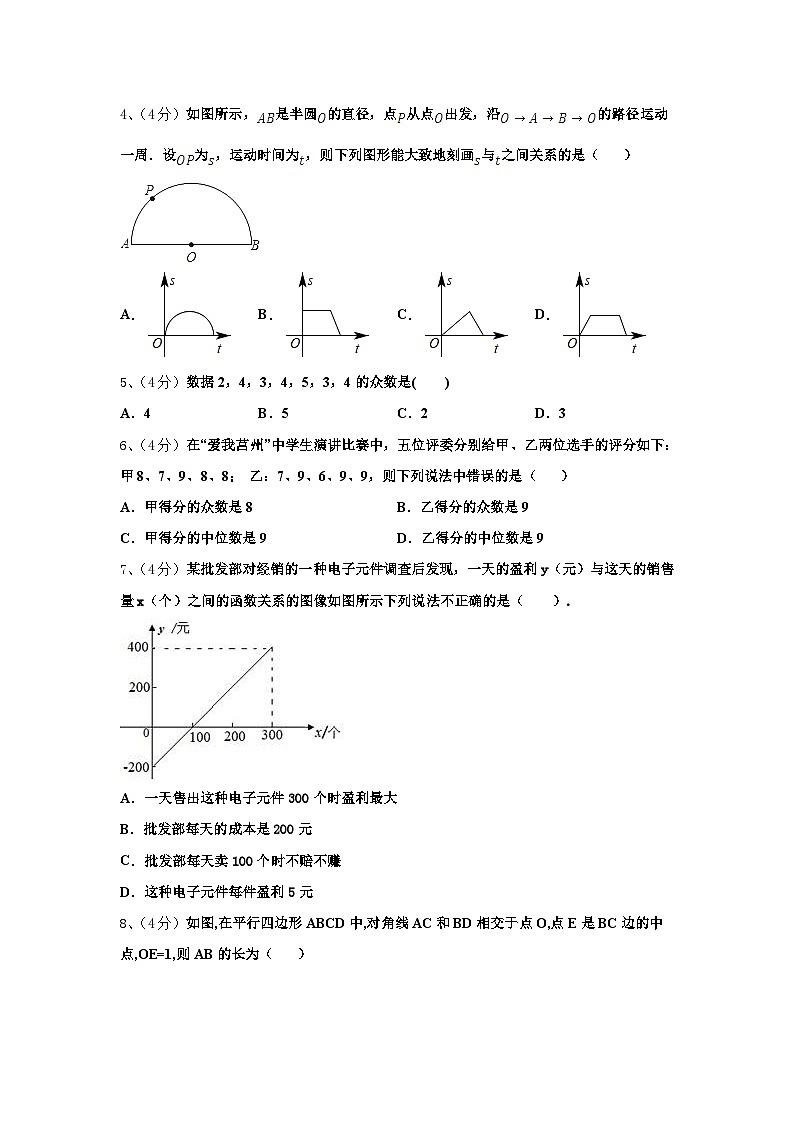
4、(4分)如图所示,是半圆的直径,点从点出发,沿的路径运动一周.设为,运动时间为,则下列图形能大致地刻画与之间关系的是( )
A.B.C.D.
5、(4分)数据2,4,3,4,5,3,4的众数是( )
A.4B.5C.2D.3
6、(4分)在“爱我莒州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:甲8、7、9、8、8; 乙:7、9、6、9、9,则下列说法中错误的是( )
A.甲得分的众数是8B.乙得分的众数是9
C.甲得分的中位数是9D.乙得分的中位数是9
7、(4分)某批发部对经销的一种电子元件调查后发现,一天的盈利y(元)与这天的销售量x(个)之间的函数关系的图像如图所示下列说法不正确的是( ).
A.一天售出这种电子元件300个时盈利最大
B.批发部每天的成本是200元
C.批发部每天卖100个时不赔不赚
D.这种电子元件每件盈利5元
8、(4分)如图,在平行四边形ABCD中,对角线AC和BD相交于点O,点E是BC边的中点,OE=1,则AB的长为( )
A.2B.1
C.D.4
二、填空题(本大题共5个小题,每小题4分,共20分)
9、(4分)在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长备几何?”这个数学问题的意思是说:“有一个水池,水面是一个边长为丈(丈尺)的正方形,在水池正中央长有一根芦苇,芦苇露出水面尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各是多少?”设这个水池的深度是尺,根据题意,可列方程为__________.
10、(4分)利用计算机中“几何画板”软件画出的函数和的图象如图所示.根据图象可知方程的解的个数为3个,若m,n分别为方程和的解,则m,n的大小关系是________.
11、(4分)若函数的图象经过A(1,)、B(-1,)、C(-2,)三点,则,,的大小关系是__________________.
12、(4分)计算的结果是______.
13、(4分)若关于x的分式方程无解,则m的值为__________.
三、解答题(本大题共5个小题,共48分)
14、(12分)如图,在△ABC中,点D、E、F分别是边AB、BC、CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)若∠AHF=20°,∠AHD=50°,求∠DEF的度数.
15、(8分)已知点E、F分别是四边形ABCD边AB、AD上的点,且DE与CF相交于点G.
(1)如图①,若AB∥CD,AB=CD,∠A=90°,且AD•DF=AE•DC,求证:DE⊥CF:
(2)如图②,若AB∥CD,AB=CD,且∠A=∠EGC时,求证:DE•CD=CF•DA:
(3)如图③,若BA=BC=3,DA=DC=4,设DE⊥CF,当∠BAD=90°时,试判断是否为定值,并证明.
16、(8分)在校园手工制作活动中,现有甲、乙两人接到手工制作纸花任务,已知甲每小时制作纸花比乙每小时制作纸花少20朵,甲制作120朵纸花的时间与乙制作160朵纸花的时间相同,求乙每小时制作多少朵纸花?
17、(10分)如图1,在ABC中,AB=AC,点D,E分别在边AB,AC上,且AD=AE,连接DE,现将ADE绕点A逆时针旋转一定角度(如图2),连接BD,CE.
(1)求证:ABD≌ACE;
(2)延长BD交CE于点F,若AD⊥BD,BD=6,CF=4,求线段DF的长.
18、(10分)小李在学校“青少年科技创新比赛”活动中,设计了一个沿直线轨道做匀速直线运动的模型.甲车从处出发向处行驶,同时乙车从处出发向处行驶.如图所示,线段、分别表示甲车、乙车离处的距离(米)与已用时间(分)之间的关系.试根据图象,解决以下问题:
(1)填空:出发_________(分)后,甲车与乙车相遇,此时两车距离处________(米);
(2)求乙车行驶(分)时与处的距离.
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19、(4分)若b为常数,且﹣bx+1是完全平方式,那么b=_____.
20、(4分)将点A(1,-3)向左平移3个单位长度,再向上平移5个单位长度后得到的点A′的坐标为 ______________.
21、(4分)实数a在数轴上的位置如图示,化简:_____.
22、(4分)评定学生的学科期末成绩由考试分数,作业分数,课堂参与分数三部分组成,并按3:2:5的比例确定,已知小明的数学考试90分,作业95分,课堂参与92分,则他的数学期末成绩为_____.
23、(4分)马拉松赛选手分甲、乙两组运动员进行了艰苦的训练,他们在相同条件下各10次比赛,成绩的平均数相同,方差分别为0.25,0.21,则成绩较为稳定的是_________(选填“甲”或“乙)
二、解答题(本大题共3个小题,共30分)
24、(8分)正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)已知点F在线段BC上.
①若AB=BE,求∠DAE度数;
②求证:CE=EF;
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.
25、(10分)如图所示,已知△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣6,0),C(﹣1,0).
(1)请直接写出点A关于原点O对称的点坐标;
(1)将△ABC向右平移6个单位,再向上平移3个单位,得到△A1B1C1,画出△A1B1C1;
(3)将△ABC绕点O逆时针转90°,得到△A1B1 C1,画出△A1B1 C1.
26、(12分)先化简,再求值,其中
参考答案与详细解析
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1、A
【解析】
由矩形的性质可得∠B=90°,AB∥CD,可得∠DCA=∠CAB,由折叠的性质可得BC=EC=4cm,AB=AE,∠E=∠B=90°,∠EAC=∠CAB=∠DCA,可得AO=OC=5cm,由勾股定理可求OE的长,即可求△ABC的面积.
【详解】
解:∵四边形ABCD是矩形
∴∠B=90°,AB∥CD
∴∠DCA=∠CAB
∵把纸片ABCD沿直线AC折叠,点B落在E处,
∴BC=EC=4cm,AB=AE,∠E=∠B=90°,∠EAC=∠CAB,
∴∠DCA=∠EAC
∴AO=OC=5cm
∴,
∴AE=AO+OE=8cm,
∴AB=8cm,
∴△ABC的面积=×AB×BC=16cm2,
故选:A.
本题考查了翻折变换,矩形的性质,勾股定理,熟练运用折叠的性质是本题的关键.
2、A
【解析】
结合图形,根据平移的概念进行求解即可得.
【详解】
解:根据平移的定义可得图案可以通过A平移得到,
故选A.
本题考查平移的基本概念及平移规律,是比较简单的几何图形变换关键是要观察比较平移前后物体的位置.
3、B
【解析】
根据分式有意义的条件是分母不等于零可得x+2≠0;解不等式可得结果,从而得出正确选项.
【详解】
由分式有意义的条件可得x+2≠0,
解得x≠-2.
故答案选B.
本题考查了分式有意义的条件,解题的关键是掌握分式有意义的条件是分母不等于零.
4、D
【解析】
依题意,可以知道点P从O到A匀速运动时,OP的长s逐渐变大;在上运动时,长度s不变;从B到O匀速运动时,OP的长s逐渐变小直至为1.依此即可求解.
【详解】
解:可以看出从O到A逐渐变大,而弧AB中的半径不变,从B到O中OP逐渐减少直至为1.
故选:D.
此题考查了函数随自变量的变化而变化的问题,能够结合图形正确分析距离y与时间x之间的大小变化关系,从而正确选择对应的图象.
5、A
【解析】
根据众数的定义求解即可.
【详解】
∵4出现的次数最多,
∴众数是4.
故选A.
本题考查了众数及中位数的定义,众数是一组数据中出现次数最多的那个数.
6、C
【解析】
众数是在一组数据中出现次数最多的数;将一组数据按从小到大顺序排列,处于最中间位置的一个数据,或是最中间两个数据的平均数称为中位数;
【详解】
∵甲8、7、9、8、8;
∴甲的众数为8,中位数为8
∵乙:7、9、6、9、9
∴已的众数为9,中位数为9
故选C.
本题考查的是众数,中位数,熟练掌握众数,中位数是解题的关键.
7、D
【解析】
分析:根据一次函数的图形特征,一一判断即可.
详解:根据图像可知售出这种电子元件300个时盈利最大,故A正确.
当售出这种电子元件0个时,利润为-200,故每天的成本为200元,故B正确.
当售出这种电子元件100个时,利润为0元,故每天卖100个时不赔不赚,故C正确.
当出售300个的利润为400元,所以每个的利润为元,故D错误.
点睛:本题是用图像表示变量间关系的问题,结合题意读懂图像是解题的关键.
8、A
【解析】
首先证明OE是△BCD的中位线,再根据平行四边形的性质即可解决问题.
【详解】
∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,
∵BE=EC,
∴OE= CD,
∵OE=1,
∴AB=CD=2,
故答案为:A
此题考查平行四边形的性质,三角形中位线定理,解题关键在于求出OE是△BCD的中位线
二、填空题(本大题共5个小题,每小题4分,共20分)
9、
【解析】
试题解析:设由题意可得:.
故答案为.
10、
【解析】
的解可看作函数与的交点的横坐标的值,可看作函数与的交点的横坐标的值,根据两者横坐标的大小可判断m,n的大小.
【详解】
解:作出函数的图像,与函数和的图象分别交于一点,所对的横坐标即为m,n的值,如图所示
由图像可得
故答案为:
本题考查了函数与方程的关系,将方程的解与函数图像相结合是解题的关键.
11、<<
【解析】
分别计算自变量为1,-1,-2对应的函数值即可得到,,的大小关系.
【详解】
解:当x=1时,=-2×1=-2;
当x=-1时,=-2×(-1)=2;
当x=-2时,=-2×(-2)=4;
∵-2<2<4
∴<<
故答案为:<<.
本题考查了正比例函数图象上点的坐标特征:正比例函数图象上点的坐标满足其解析式.
12、1
【解析】
利用二次根式的计算法则正确计算即可.
【详解】
解:
=
=
=1
故答案为:1.
本题考查的是二次根式的混合运算,掌握计算法则是解题关键.
13、
【解析】
由分式方程无解得到x=5,将其代入化简后的整式方程即可求出答案.
【详解】
将方程去分母得到:x-2(x-5)=-m,即10-x=-m,
∵分式方程无解,
∴x=5,
将x=5代入10-x=-m中,解得m=-5,
故答案为:-5.
此题考查分式方程无解的情况,正确理解分式方程无解的性质得到整式方程的解是解题的关键.
三、解答题(本大题共5个小题,共48分)
14、(1)见解析;(2)70°.
【解析】
(1)结合中位线的性质证明即可;(2)先根据平行四边形的性质得到∠DEF=∠BAC,再根据题意证明∠DHF=∠BAC,得到∠DEF=∠DHF,计算∠DHF大小即可.
【详解】
(1)∵D,E,F分别是边AB、BC、CA的中点,
∴DE,EF是△ABC的中位线,
∴DE∥AF,EF∥AD,
∴四边形ADEF是平行四边形.
(2)∵四边形ADEF是平行四边形,
∴∠DEF=∠BAC,
∵D,F分别是AB,CA的中点,AH是边BC上的高,
∴DH=AD,FH=AF,
∴∠DAH=∠DHA,∠FAH=∠FHA,
∵∠DAH+∠FAH=∠BAC,
∠DHA+∠FHA=∠DHF,
∴∠DHF=∠BAC,
∴∠DEF=∠DHF=∠AHF+∠AHD=70°.
本题主要考查中位线的性质和平行四边形的判定与性质,掌握中位线的性质,证明∠DEF=∠DHF是解答本题的关键.
15、(1)证明见解析 (2)证明见解析 (3)答案见解析
【解析】
(1)根据已知条件得到四边形ABCD是矩形,由矩形的性质得到∠A=∠FDC=90°,根据相似三角形的性质得到∠CFD=∠AED,根据余角的性质即可得到结论;
(2)根据已知条件得到△DFG∽△DEA,推出,根据△CGD∽△CDF,得到
,等量代换即可得到结论;
(3)过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,△BAD≌△BCD,推出∠BCD=∠A=90°,证△BCM∽△DCN,求出,在Rt△CMB中,由勾股定理得出BM2+CM2=BC2,解方程得到CN,证出△AED∽△NFC,即可得出答案.
【详解】
(1)证明:∵AB∥CD,AB=CD,∠A=90°,
∴四边形ABCD是矩形,
∴∠A=∠FDC=90°,
∵AD•DF=AE•DC,
∴
∴△AED∽△DFC,
∴∠CFD=∠AED,
∵∠ADE+∠AED=90°,
∴∠ADE+∠CFD=90°,
∴∠DGF=90°,
∴DE⊥CF;
(2)证明:∵∠A=∠EGC,∠ADE=∠GDF,
∴△DFG∽△DEA,
∴
∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,∠AED=∠EDC,
∴∠B=∠ADC,
∵△DFG∽△DEA,
∴∠AED=∠DFG,
∴DFC=∠GDC,
∵∠DCG=∠FCD,
∴△CGD∽△CDF,
∴
∴,
∴DE•CD=CF•DA;
(3)解:为定值,
理由:过C作CN⊥AD于N,CM⊥AB交AB延长线于M,连接BD,设CN=x,
∵∠BAD=90°,即AB⊥AD,
∴∠A=∠M=∠CNA=90°,
∴四边形AMCN是矩形,
∴AM=CN,AN=CM,
∵在△BAD和△BCD中,
∴△BAD≌△BCD(SSS),
∴∠BCD=∠A=90°,
∴∠ABC+∠ADC=180°,
∵∠ABC+∠CBM=180°,
∴∠MBC=∠ADC,
∵∠CND=∠M=90°,
∴△BCM∽△DCN,
∴,
∴
∴
在Rt△CMB中,,BM=AM﹣AB=x﹣3,由勾股定理得:BM2+CM2=BC2,
∴
x=0(舍去),
∴
∵∠A=∠FGD=90°,
∴∠AED+∠AFG=180°,
∵∠AFG+∠NFC=180°,
∴∠AED=∠CFN,
∵∠A=∠CNF=90°,
∴△AED∽△NFC,
∴
属于相似三角形的综合题,考查矩形的性质,全等三角形的判定与性质,相似三角形的判定与性质,综合性比较强,掌握相似三角形的判定定理是解题的关键.
16、乙每小时制作80朵纸花.
【解析】
设乙每小时制作x朵纸花,则甲每小时制作x-20朵纸花,根据“甲制作120朵纸花的时间与乙制作160朵纸花的时间相同”得:,解分式方程可得.
【详解】
解:设乙每小时制作x朵纸花,依题意得:
解得:,
经检验,是原方程的解,且符合题意.
答:乙每小时制作80朵纸花.
本题考核知识点:列分式方程解应用题.解题关键点:找出相等关系,列方程.
17、(1)见解析;(2)2
【解析】
(1)由“SAS”可证△ABD≌△ACE;
(2)由全等三角形的性质可得BD=CE=6,∠AEC=∠ADB=90°,由“HL”可证Rt△AEF≌Rt△ADF,可得DF=EF=2.
【详解】
证明:(1)由图1可知:∠DAE=∠BAC,
∴∠DAE+∠CAD=∠BAC+∠CAD,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS);
(2)如图2,连接AF,
∵AD⊥BD,
∴∠ADB=∠ADF=90°,
∵△ABD≌△ACE,
∴BD=CE=6,∠AEC=∠ADB=90°,
∴EF=CE﹣CF=2,
∵AF=AF,AD=AE,
∴Rt△AEF≌Rt△ADF(HL),
∴DF=EF=2.
此题考查旋转的性质,全等三角形的判定及性质定理,熟记三角形全等的判定定理,确定对应相等的线段或角的关系由此证明三角形全等是解题的关键.
18、(1)0.6,2.4;(2)4.8米
【解析】
(1)甲乙相遇即图象交点(0.6,2.4)
(2)根据图象解出两条直线的解析式,再由题意得到乙车行驶1.2(分)时与B处的距离.
【详解】
(1)甲乙相遇即图象交点(0.6,2.4)
∴出发0.6(分)后,甲车与乙车相遇,此时两车距离B处2.4(米);
故答案为0.6和2.4
(2)假设直线l2的解析式为y=kx,将点(0.6,2.4)代入得,y=4x
当x=1.2时,y=4.8
∴乙车行驶12(分)时与B处距离为4.8米.
本题主要考查一次函数的应用,熟练掌握一次函数是解答本题的关键.
一、填空题(本大题共5个小题,每小题4分,共20分)
19、±1
【解析】
根据完全平方式的一般式,计算一次项系数即可.
【详解】
解:∵b为常数,且x2﹣bx+1是完全平方式,
∴b=±1,
故答案为±1.
本题主要考查完全平方公式的系数关系,关键在于一次项系数的计算.
20、 (-2,2)
【解析】
由题意根据点向左平移横坐标减,向上平移纵坐标加求解即可.
【详解】
解:∵点A(1,-3)向左平移3个单位长度,再向上平移5个单位长度后得到点A′,
∴点A′的横坐标为1-3=-2,纵坐标为-3+5=2,
∴A′的坐标为(-2,2).
故答案为:(-2,2).
本题考查坐标与图形变化-平移,注意掌握平移时点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
21、1.
【解析】
由数轴可知,1
相关试卷
这是一份2024年上海市民办新竹园中学数学九上开学质量跟踪监视模拟试题【含答案】,共26页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2024年山东德州经开区抬头寺中学数学九上开学质量跟踪监视模拟试题【含答案】,共21页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2024年湖北省黄冈市初级中学数学九上开学质量跟踪监视模拟试题【含答案】,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。









