2024年浙江省宁波北仑区东海实验学校数学九上开学质量检测试题【含答案】

这是一份2024年浙江省宁波北仑区东海实验学校数学九上开学质量检测试题【含答案】，共22页。试卷主要包含了选择题，解答题等内容，欢迎下载使用。
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、（4分）若一次函数y＝(k－3)x－k的图象经过第二、三、四象限，则k的取值范围是( )
A．k＜3B．k＜0C．k＞3D．0＜k＜3
2、（4分）已知反比例函数，在每个象限内y随着x的增大而增大，点P（a－1， 2）在这个反比例函数上，a的值可以是（ ）
A．0B．1C．2D．3
3、（4分）菱形具有而一般平行四边形不具有的性质是( )
A．对边相等 B．对角相等 C．对角线互相平分 D．对角线互相垂直
4、（4分）若＝﹣a，则a的取值范围是（ ）
A．﹣3≤a≤0B．a≤0C．a＜0D．a≥﹣3
5、（4分）如图，点是矩形两条对角线的交点，E是边上的点，沿折叠后，点恰好与点重合．若，则折痕的长为 ( )
A．B．C．D．6
6、（4分）函数自变量的值可以是（ ）
A．-1B．0C．1D．2
7、（4分）方程的解是（ ）
A．B．C．D．
8、（4分）一次函数的图像经过（ ）
A．第一、二、三象限B．第二、三、四象限C．第一、三、四象限D．第一、二、四象限
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（4分）把多项式n（n﹣2）+m（2﹣n）分解因式的结果是_____．
10、（4分）一个多边形的内角和等于 1800°，它是______边形．
11、（4分）某市出租车的收费标准是：千米以内（包括千米）收费元，超过千米，每增加千米加收元，则当路程是（千米）（）时，车费（元）与路程（千米）之间的关系式（需化简）为：________.
12、（4分）如图，△ABC中，BD⊥CA，垂足为D，E是AB的中点，连接DE．若AD＝3，BD＝4，则DE的长等于_____
13、（4分）李明的座位在第5排第4列，简记为（5，4），张扬的座位在第3排第2列，简记为，若周伟的座位在李明的前面相距2排，同时在他的右边相距2列，则周伟的座位可简记为___________________．
三、解答题（本大题共5个小题，共48分）
14、（12分）化简并求值：，其中x=﹣1．
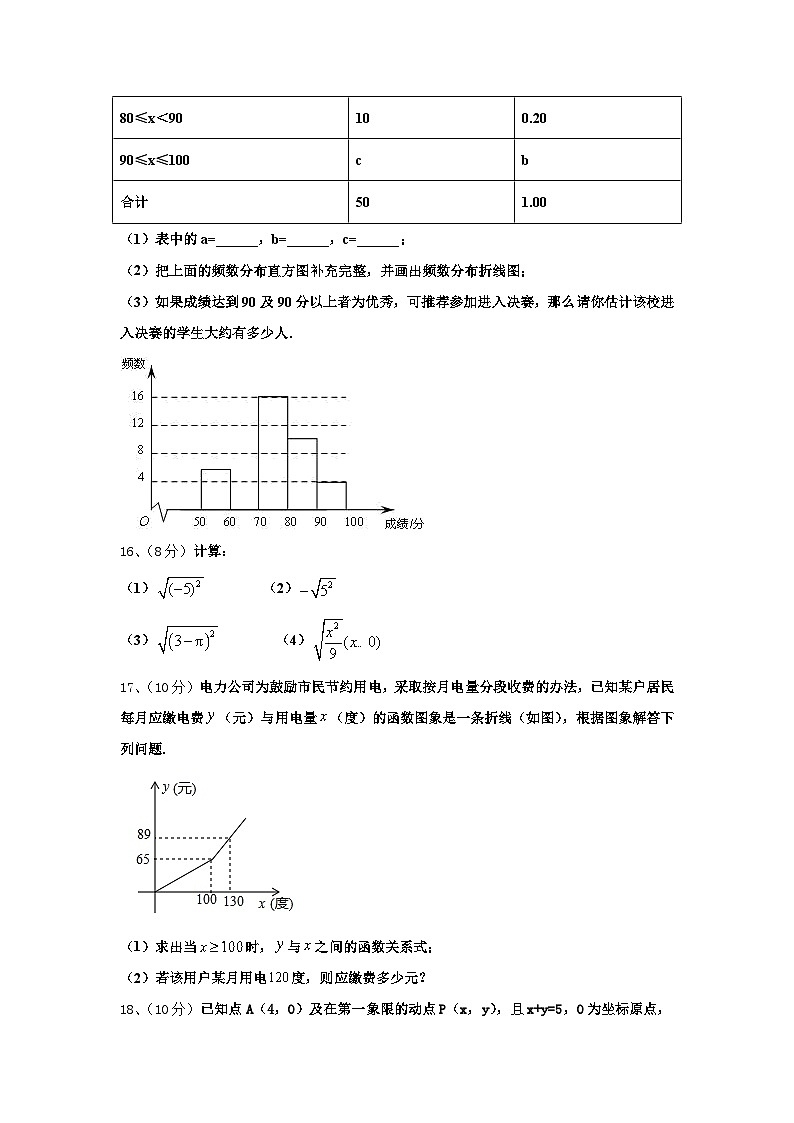
15、（8分）为弘扬中华传统文化，了解学生整体听写能力，某校组织全校1000名学生进行一次汉字听写大赛初赛，从中抽取部分学生的成绩进行统计分析，根据测试成绩绘制出了频数分布表和频数分布直方图：
（1）表中的a=______，b=______，c=______；
（2）把上面的频数分布直方图补充完整，并画出频数分布折线图；
（3）如果成绩达到90及90分以上者为优秀，可推荐参加进入决赛，那么请你估计该校进入决赛的学生大约有多少人．
16、（8分）计算：
（1） （2）
（3） （4）
17、（10分）电力公司为鼓励市民节约用电，采取按月电量分段收费的办法，已知某户居民每月应缴电费（元）与用电量（度）的函数图象是一条折线（如图），根据图象解答下列问题.
（1）求出当时，与之间的函数关系式；
（2）若该用户某月用电度，则应缴费多少元？
18、（10分）已知点A（4，0）及在第一象限的动点P（x，y），且x+y=5，0为坐标原点，设△OPA的面积为S．
（1）求S关于x的函数表达式；
（2）求x的取值范围；
（3）当S=4时，求P点的坐标．
B卷（50分）
一、填空题（本大题共5个小题，每小题4分，共20分）
19、（4分）已知关于x的分式方程＝1的解是非负数，则m的取值范围是_____．
20、（4分）若关于x的分式方程有增根，则a的值为_______
21、（4分）若关于的方程无解，则的值为________．
22、（4分）根据图中的程序，当输入数值﹣2时，输出数值为a；若在该程序中继续输入数值a时，输出数值为_____．
23、（4分）已知一次函数的图像经过点，那么这个一次函数在轴上的截距为__________．
二、解答题（本大题共3个小题，共30分）
24、（8分）如图 1，在正方形 ABCD 中，对角线 AC, BD 交于点 O ，点 E 在 AB 上，点 F 在 BC 的延长线上，且 AE  CF .连接 EF 交 AC 于点 P, 分别连接 DE, DF .
（1）求证： ADE  CDF ;
（2）求证： PE  PF ;
（3）如图 2，若 PE  BE, 则的值是 .（直接写出结果即可）.
25、（10分）已知：如图，平面直角坐标系中，，，点C是x轴上一点，点D为OC的中点．
（1）求证：BD∥AC；
（2）若点C在x轴正半轴上，且BD与AC的距离等于2，求点C的坐标；
（3）如果于点E，当四边形ABDE为平行四边形时，求直线AC的解析式．
26、（12分）（1）某学校“智慧方园”数学社团遇到这样一个题目：
如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=，BO：CO=1：3，求AB的长．
经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．
请回答：∠ADB= °，AB= ．
（2）请参考以上解决思路，解决问题：
如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO=，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长．
参考答案与详细解析
一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求）
1、D
【解析】
由一次函数图象经过第二、三、四象限，利用一次函数图象与系数的关系，即可得出关于k的一元一次不等式组，解之即可得出结论．
【详解】
∵一次函数y=（k-3）x-k的图象经过第二、三、四象限，
∴，
解得：0＜k＜3，
故选：D．
本题考查了一次函数图象与系数的关系，牢记“k＜0，b＜0⇔y=kx+b的图象在二、三、四象限”是解题的关键．
2、A
【解析】
根据函数的增减性判断出图象所在象限，进而得出图象上点的坐标特征，将四个选项的数值代入P（a-1，2）验证即可．
解：∵反比例函数，在每个象限内y随着x的增大而增大，
∴函数图象在二、四象限，
∴图象上的点的横、纵坐标异号．
A、a=0时，得P（-1，2），故本选项正确；
B、a=1时，得P（0，2），故本选项错误；
C、a=2时，得P（1，2），故本选项错误；
D、a=3时，得P（2，2），故本选项错误．
故选A．
此题考查了反比例函数图象上点的坐标特征，要熟悉反比例函数的性质，同时要注意数形结合．
3、D
【解析】
试题分析：∵菱形具有的性质：对边相等，对角相等，对角线互相平分，对角线互相垂直；
平行四边形具有的性质：对边相等，对角相等，对角线互相平分；
∴菱形具有而一般平行四边形不具有的性质是：对角线互相垂直．
故选D．
考点：菱形的性质；平行四边形的性质．
4、A
【解析】
根据二次根式的性质列出不等式，解不等式即可解答.
【详解】
∵= =﹣a，
∴a≤0，a+3≥0，
∴﹣3≤a≤0.
故选A.
本题考查二次根式的性质，根据二次根式的性质列出不等式是解题的关键.
5、A
【解析】
由矩形的性质可得OA=OC，根据折叠的性质可得OC=BC，∠COE=∠B=90°，即可得出BC=AC，OE是AC的垂直平分线，可得∠BAC=30°，根据垂直平分线的性质可得CE=AE，根据等腰三角形的性质可得∠OCE=∠BAC=30°，在Rt△OCE中利用含30°角的直角三角形的性质即可求出CE的长.
【详解】
∵点O是矩形ABCD两条对角线的交点，
∴OA=OC，
∵沿CE折叠后，点B恰好与点O重合．BC=3，
∴OC=BC=3，∠COE=∠B=90°，
∴AC=2BC=6，OE是AC的垂直平分线，
∴AE=CE，
∵∠B=90°，BC=AC，
∴∠BAC=30°，
∴∠OCE=∠BAC=30°，
∴OC=CE，
∴CE=2.
故选A.
本题考查折叠的性质、矩形的性质及含30°角的直角三角形的性质，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等；矩形的对角线相等且互相平分；30°角所对的直角边等于斜边的一半.熟练掌握相关性质是解题关键.
6、C
【解析】
根据分母不能等于零，可得答案．
【详解】
解：由题意，
得，
解得，
故选：C.
本题考查了函数自变量的取值范围，利用分母不能等于零得出不等式是解题关键．
7、C
【解析】
根据方程即可得出两个一元一次方程，求出方程的解即可.
【详解】
解：由，得
x=0，x+2=0
∴
故选C.
本题考查了解一元二次方程. 能把一元二次方程转化为一元一次方程是解此题的关键.
8、D
【解析】
根据一次函数的性质k＜0，则可判断出函数图象y随x的增大而减小，再根据b＞0，则函数图象一定与y轴正半轴相交，即可得到答案．
【详解】
解：∵一次函数y=-2x+3中，k=-2＜0，则函数图象y随x的增大而减小，
b=3＞0，则函数图象一定与y轴正半轴相交，
∴一次函数y=-2x+3的图象经过第一、二、四象限．
故选：D．
本题考查了一次函数的图象，一次函数y=kx+b的图象经过的象限由k、b的值共同决定，分如下四种情况：①当k＞0，b＞0时，函数y=kx+b的图象经过第一、二、三象限；②当k＞0，b＜0时，函数y=kx+b的图象经过第一、三、四象限；③当k＜0，b＞0时，函数y=kx+b的图象经过第一、二、四象限；④当k＜0，b＜0时，函数y=kx+b的图象经过第二、三、四象．
二、填空题（本大题共5个小题，每小题4分，共20分）
9、（n﹣2）（n﹣m）．
【解析】
用提取公因式法分解因式即可．
【详解】
n（n﹣2）+m（2﹣n）= n（n﹣2）-m（n-2）=（n﹣2）（n﹣m）．
故答案为（n﹣2）（n﹣m）．
本题考查了用提公因式法进行因式分解；一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．
10、十二
【解析】
根据多边形的内角和公式列方程求解即可；
【详解】
设这个多边形是n边形，
由题意得，（n-2）•180°=1800°，
解得n=12；
故答案为十二
本题考查了多边形的内角和，关键是掌握多边形的内角和公式．
11、
【解析】
根据题意可以写出相应的函数关系式，本题得以解决．
【详解】
由题意可得，
当x＞3时，
y=5+（x-3）×1.2=1.2x+1.1，
故答案为：y=1.2x+1.1．
本题考查一次函数的应用，解答本题的关键是明确题意，写出相应的函数解析式．
12、2.1
【解析】
根据勾股定理求出AB，根据直角三角形斜边上中线性质得出DE＝AB，代入求出即可．
【详解】
.解：∵BD⊥CA，
∴∠ADB＝90°，
在Rt△ADB中，由勾股定理得：AB＝ ＝＝1，
∵E是AB的中点，∠ADB＝90°，
∴DE＝AB＝2.1，
故答案为：2.1．
本题考查了勾股定理和直角三角形斜边上中线的性质，能求出AB的长和得出DE＝AB是解此题的关键．
13、（3，6）
【解析】
先求出周伟所在的排数与列数，再根据第一个数表示排数，第二个数表示列数解答．
【详解】
解：∵周伟的座位在李明的前面相距2排，同时在他的右边相距2列，
∴周伟在第3排第6列，
∴周伟的座位可简记为（3，6）．
故答案为：（3，6）．
本题考查坐标确定位置，读懂题目信息，理解有序数对的两个数的实际意义是解题关键．
三、解答题（本大题共5个小题，共48分）
14、2.
【解析】
试题分析：先将进行化简，再将x的值代入即可;
试题解析：
原式=﹣•（x﹣1）==，
当x=﹣1时，原式=﹣2．
15、（1）14；0.08；4；（2）详见解析；（3）80.
【解析】
（1）根据频率分布表确定出总人数，进而求出a，b，c的值即可；
（2）把上面的频数分布直方图补充完整，并画出频数分布折线图，如图所示；
（3）根据样本中90分及90分以上的百分比，乘以1000即可得到结果．
【详解】
解：（1）根据题意得：a=6÷0.12×0.28=14，b=1﹣（0.12+0.28+0.32+0.20）=0.08，c=6÷0.12×0.08=4；
故答案为：14；0.08；4；
（2）频数分布直方图、折线图如图，

（3）根据题意得：1000×（4÷50）=80（人），
则你估计该校进入决赛的学生大约有80人．
此题考查了频数（率）分布折线图，用样本估计总体，频数（率）分布表，以及频数（率）分布直方图，弄清题中的数据是解本题的关键.
16、（1）5；（2）-5；（3）；（4）
【解析】
根据算术平方根的定义以及二次根式的性质，分别对（1）（2）（3）（4）进行化简计算即可．
【详解】
解：（1）
（2）
（3）
（4）
本题主要考查了算术平方根的定义，熟练掌握二次根式的性质是解答本题的关键．
17、（1）；（2）用电度，应缴费元
【解析】
（1）本题考查的是分段函数的知识．依题意可以列出函数关系式；
（2）根据（1）中的函数解析式以及图标即可解答．
【详解】
解：（1）设与的关系式为,
射线过点、,
,
解得.
与的关系式是.
（2）当时，
.
用电度，应缴费元.
本题主要考查一次函数的应用以及待定系数法求函数解析式，解决问题的关键是从一次函数的图象上获取信息．
18、（1）S=10﹣2x；（2）0＜x＜5；（3）（3，2）
【解析】
(1)根据题意画出图形,由x＋y＝5可知y＝5﹣x ,再由三角形的面积公式即可得出结论;
(2)由点P（x，y）在第一象限,且x＋y＝5得出x的取值范围即可;
(3)把S＝4代入(1)中的关系式求出x的值,进而可得出y的值.
【详解】
（1）如图：
∵x＋y＝5，
∴y＝5﹣x，
∴S＝×4×（5﹣x）＝10﹣2x；
（2）∵点P（x，y）在第一象限，且x＋y＝5，
∴0＜x＜5；
（3）∵由（1）知，S＝10﹣2x，
∴10﹣2x＝4，解得x＝3，
∴y＝2，
∴P（3，2）．
本题考查的是一次函数的性质,根据题意画出图形,利用数形结合求解是解答此题的关键.
一、填空题（本大题共5个小题，每小题4分，共20分）
19、m≥1
【解析】
由分式方程的解为非负数得到关于m的不等式，进而求出m的范围即可．
【详解】
解：分式方程去分母得：m=x+1，
即x=m-1，
由分式方程的解为非负数，得到
m-1≥0，且m-1≠-1，
解得：m≥1，
故答案为m≥1．
本题考查了分式方程的解，在解方程的过程中因为在把分式方程化为整式方程的过程中，扩大了未知数的取值范围，可能产生增根，增根是令分母等于0的值，不是原分式方程的解．
20、3
【解析】
先根据分式方程的求解去掉分式方程的分母，再把增根x=5代入即可求出a的值.
【详解】
解
去分母得2-(x-a)=7(x-5)
把x=5代入得2-（5-a）=0，解得a=3
故填：3.
此题主要考查分式方程的求解，解题的关键是熟知分式方程增根的定义.
21、
【解析】
分式方程去分母转化为整式方程，由分式方程无解得到x+1=0，求出x的值，代入整式方程求出m的值即可．
【详解】
去分母得：3x−2=2x+2+m，
由分式方程无解，得到x+1=0，即x=−1，
代入整式方程得：−5=−2+2+m，
解得：m=−5，
故答案为-5.
此题考查分式方程的解，解题关键在于掌握运算法则.
22、8 ．
【解析】
观察图形我们可以得出x和y的关系式为：是x≥1时关系式为y=x+5，当x＜1是y=−x+5，然后将x=-2代入y=−x+5，求出y值即a值，再把a值代入关系式即可求出结果.
【详解】
当x=-2时，
∵x=−2