2024-2025学年黑龙江省大庆市肇州中学九年级（上）第一次质检数学试卷（五四学制）（含解析）

这是一份2024-2025学年黑龙江省大庆市肇州中学九年级（上）第一次质检数学试卷（五四学制）（含解析），共29页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.−|−2024|的倒数是( )
A. 12024B. 2024C. −2024D. −12024
2.下列手机手势解锁图案中，是中心对称图形的是( )
A. B. C. D.
3.下列各式中，一定是二次根式的是( )
A. −2B. 33C. a2+1D. a−1
4.下列说法中，正确的是( )
A. 对角线互相垂直的四边形是菱形B. 对角线相等的四边形是矩形
C. 对角线互相垂直的四边形是正方形D. 对角线相等的菱形是正方形
5.经过某十字路口的汽车，可能直行，也可能向左转或向右转，如果这三种可能性大小相同，那么两辆汽车经过这个十字路口时，第一辆车向左转，第二辆车向右转的概率是( )
A. 13B. 19C. 29D. 427
6.下面四个图中反比例函数的表达式均为y=3x，则阴影部分的图形的面积为3的有( )
A. 1个B. 2个C. 3个D. 4个
7.如图，四边形ABCD是菱形，对角线AC，BD相交于点O，AC=8.BD=6，点E是CD上一点，连接OE，若OE=CE，则OE的长是( )
A. 2
B. 52
C. 3
D. 4
8.如图，是由四个全等的直角三角形拼成的“赵爽弦图”，得到正方形ABCD与正方形EFGH，连结DF.若S正方形ABCD=5，EF=12BG，则DF的长为( )
A. 2
B. 5
C. 3
D. 2 2
9.如图，D是等边三角形△ABC边上的点，AD=3，BD=5，现将△ABC折叠，使点C与点D重合，折痕为EF，且点E点F分别在边AC和BC上，则CECF的值为( )
A. 1113
B. 35
C. 45
D. 89
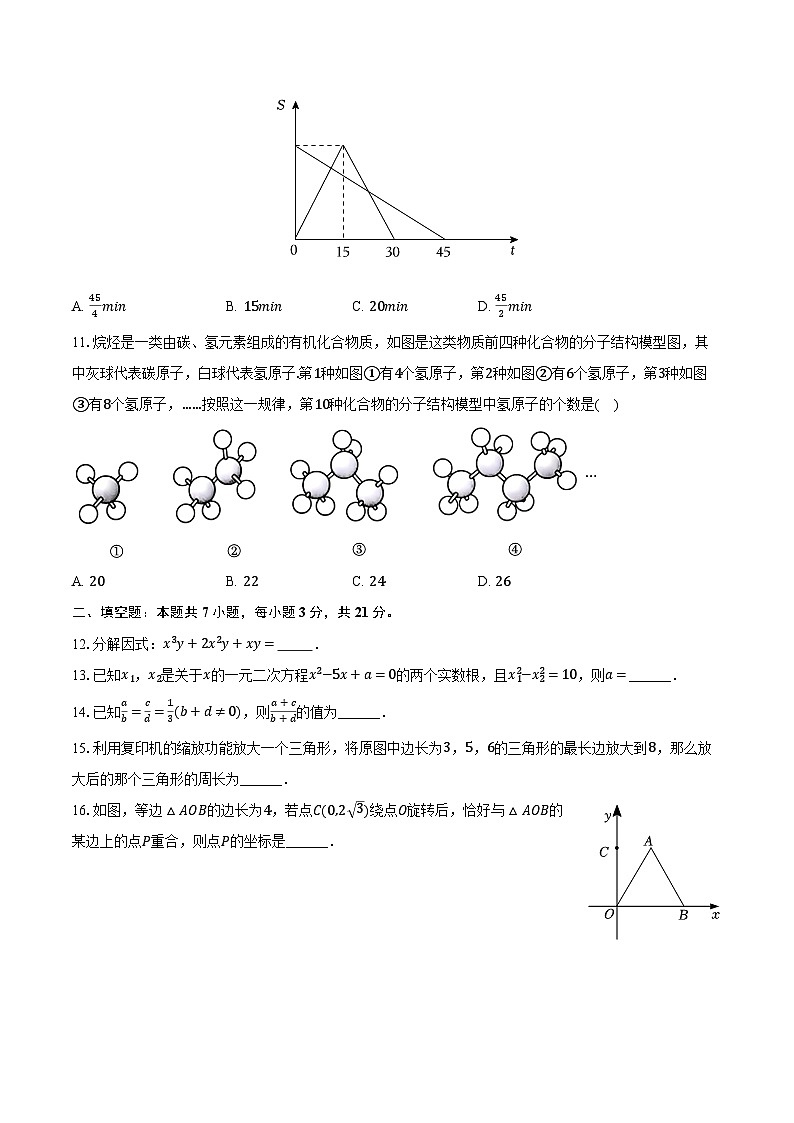
10.甲、乙两车同时从A、B两地出发，相向而行，甲车到达B地后立即返回A地，两车离A地的路程S(单位：km)与所用时间t(单位：min)之间的函数关系如图所示，则甲、乙两车在途中两次相遇的间隔时间为( )
A. 454minB. 15minC. 20minD. 452min
11.烷烃是一类由碳、氢元素组成的有机化合物质，如图是这类物质前四种化合物的分子结构模型图，其中灰球代表碳原子，白球代表氢原子.第1种如图①有4个氢原子，第2种如图②有6个氢原子，第3种如图③有8个氢原子，……按照这一规律，第10种化合物的分子结构模型中氢原子的个数是( )
A. 20B. 22C. 24D. 26
二、填空题：本题共7小题，每小题3分，共21分。
12.分解因式：x3y+2x2y+xy= ．
13.已知x1，x2是关于x的一元二次方程x2−5x+a=0的两个实数根，且x12−x22=10，则a=______．
14.已知ab=cd=13(b+d≠0)，则a+cb+d的值为______．
15.利用复印机的缩放功能放大一个三角形，将原图中边长为3，5，6的三角形的最长边放大到8，那么放大后的那个三角形的周长为______．
16.如图，等边△AOB的边长为4，若点C(0,2 3)绕点O旋转后，恰好与△AOB的某边上的点P重合，则点P的坐标是______．
17.如图，在平面直角坐标系中，Rt△ABC的斜边AB在x轴上，∠ACB=90°，∠CAB=30°，点A的坐标为(1,0)，将△ABC绕着点B旋转60°得到△DBE，若反比例函数y=kx的图象经过点D和点E，则k的值为______．
18.如图，在矩形ABCD中，AD= 2AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：
①∠AED=∠CED；②OE=OD；③BH=HF；④BC−CF=2HE；⑤AB=HF，
其中正确的有______．
三、解答题：本题共10小题，共80分。解答应写出文字说明，证明过程或演算步骤。
19.(本小题8分)
计算：− 2sin45°+(−1)2024+(−12)−1+ 18．
20.(本小题8分)
先化简，再求代数式(1x+1−1x−1)÷x+1x2+2x+1的值，其中x=3tan30°+ 2cs45°．
21.(本小题8分)
如图，在平面直角坐标系中，一次函数y=−32x+b与反比例函数y=kx(k≠0)交于A(m,6)，B(4,−3)两点，与y轴交于点C，连接OA，OB．
(1)求反比例函数和一次函数的表达式；
(2)求△AOB的面积．
22.(本小题8分)
已知菱形ABCD的边长是5，两条对角线AC、BD交于点O，且A0、B0的长分别是关于x的方程x2+(2m−1)x+m2+3=0的两根．
(1)求m的值．
(2)求菱形ABCD的面积．
23.(本小题8分)
某校以“我最喜爱的体育运动”为主题对全校学生进行随机抽样调查，调查的运动项目有：篮球、羽毛球、乒乓球、跳绳及其它项目(要求每人必须参加且每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图：
请根据图表信息解答下列问题：
(1)频数分布表中的m= ______，n= ______；
(2)在扇形统计图中，“乒乓球”所在的扇形的圆心角的度数为______；
(3)从喜爱跳绳运动表现优秀的甲、乙、丙、丁四名同学中随机选取两名参加跳绳比赛，请用列表或画树状图的方法求出恰好选中甲和乙两名同学的概率．
24.(本小题8分)
宝安公明腊肠是深受当地民众喜爱的一种美食，其制作技艺至今已有百余年历史，该项目2017年被列入宝安区区级非物质文化遗产保护名录.某腊肠制作坊计划购买A，B两种香料制作腊肠.已知购买1千克A种香料和1千克B种香料共需60元，购买3千克A种香料和4千克B种香料共需220元．
(1)求A，B两种香料的单价；
(2)该小吃店计划购买两种香料共20千克，其中购买A种香料的重量不超过B种香料重量的3倍，当A，B两种香料分别购买多少千克时，总费用最少？并求出最少总费用．
25.(本小题8分)
中国的探月工程激发了同学们对太空的兴趣.某晚，淇淇在家透过窗户的最高点P恰好看到一颗星星，此时淇淇距窗户的水平距离BQ=4m，仰角为α；淇淇向前走了3m后到达点D，透过点P恰好看到月亮，仰角为β，如图是示意图.已知，淇淇的眼睛与水平地面BQ的距离AB=CD=1.6m，点P到BQ的距离PQ=2.6m，AC的延长线交PQ于点E.(注：图中所有点均在同一平面)
(1)求β的大小及tanα的值；
(2)求CP的长及sin∠APC的值．
26.(本小题8分)
如图，菱形ABCD中，AB=4 3，连接BD，点P是线段BC上一点(不与点B重合)，AP与对角线BD交于点E，连接EC．
(1)求证：∠BAE=∠BCE；
(2)若∠ABC=60°，BP= 3，求BE的长．
27.(本小题8分)
知识再现
如图1，在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边分别为a，b，c．
∵sinA=ac，sinB=bc
∴c=asinA，c=bsinB．
∴asinA=bsinB．
拓展探究
如图2，在锐角△ABC中，∠A，∠B，∠C的对边分别为a，b，c．
请探究asinA，bsinB，csinC之间的关系，并写出探究过程．
解决问题
如图3，为测量点A到河对岸点B的距离，选取与点A在河岸同一侧的点C，测得AC=60m，∠A=75°，∠C=60°.请用拓展探究中的结论，求点A到点B的距离．
28.(本小题8分)
在△ABC中，∠ACB=90°，BC=3，AC=4，点P是AB的中点，M在AC上(不与点C重合)，连接PM，在PM的左侧作矩形PMQN．
(1)如图1，当点N在线段BC上时，
①若AM=2，求PN的长；
②求tan∠PNM的值．
(2)如图2，当PN=PM时，
①若矩形PMQN在△ABC内部(包括边界)，设AM=x，写出CQ的长与x的函数关系式，并求x的取值范围；
②若矩形PMQN的两个顶点落在△PCA的同一条边上，直接写出AC在矩形PMQN内部的线段长．
答案和解析
1.【答案】D
【解析】解：−|−2024|=−2024，则它的倒数为−12024，
故选：D．
由题意可得−|−2024|=−2024，然后根据倒数的定义即可求得答案．
本题考查绝对值及倒数，熟练掌握其定义是解题的关键．
2.【答案】B
【解析】解：A、不是中心对称图形，故此选项不合题意；
B、是中心对称图形，故此选项符合题意；
C、不是中心对称图形，故此选项不合题意；
D、不是中心对称图形，故此选项不合题意．
故选：B．
中心对称图形：在同一平面内，如果把一个图形绕某一点旋转180°，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形．
本题考查了中心对称图形的概念，掌握中心对称图形是要寻找对称中心，旋转180度后与原图重合是关键．
3.【答案】C
【解析】解：A、 −2的被开方数−20，是二次根式，故此选项符合题意；
D、 a−1的被开方数a−1有可能小于0，即当a0，
∴(2m−1)2−4(m2+3)>0，
解得m