初中数学人教版（2024）七年级上册2.1 整式同步测试题

这是一份初中数学人教版（2024）七年级上册2.1 整式同步测试题，共17页。试卷主要包含了用代数式表示，用字母表示运算律，填空题等内容，欢迎下载使用。
基础训练
1．下列各式中，符合代数式书写要求的是（ ）．
A．B．C．D．
2．用代数式表示：“a，b两数的平方和与a，b乘积的差”，正确的是（ ）
A． B． C． D．
3．若表示一个两位数，也表示一个两位数，小明想用、来组成一个四位数，且把放在的左边，你认为下列表达式中哪一个是正确的（ ）
A．B．C．D．
4．甲，乙两商场以相同的价格出售同样的商品，当购物金额超出一定数额后，各自推出不同的优惠方案，若在两个商场购买元的商品，在甲商场需付费元，在乙商场需付费元，下列关于两个商场优惠方案的说法正确的是（ ）
A．购买金额不超过100元时，两个商场都不优惠
B．购买金额超过50元时，两个商场都有优惠
C．购买金额超过100元时，甲商场按收费，乙商场按收费
D．购买金额超过100元时，超出100元的部分，甲商场按收费，乙商场按收费
5．如果设正方形纸的边长为acm，所折无盖长方体形盒子的高为hcm，用a与h来表示这个无盖长方体形盒子的容积是（ ）
A．B．C．D．
6．某商品原价为a元，先提高20%，然后连续两次降价，每次降价10%．则该商品的价格是（ ）
A．元B．元C．元D． 元
7．下列用字母表示数的式子中，符合书写要求的有 个．
，，，，，
8．用字母表示运算律：如果用a、b、c分别表示有理数，那么加法交换律可以表示成： ；加法结合律可以表成： ；乘法交换律可以表示成： ；乘法结合律可以表成： ；乘法对加法的分配律可以表示成： ．
9．填空题
（1）某种足球元，则涨价20%后是 元；
（2）箱橘子重kg，每箱重 kg；
（3）购买单价为元的笔记本8本，共需人民币 元；
（4）小明的体重是kg，小红比小明重kg，则小红的体重是 kg；
（5）张师傅第一天生产个零件，第二天比第一天减少5%，第二天生产零件 个．
10．某超市的苹果价格如图，试说明代数式100﹣9.8x的实际意义 ．
11．现有5元面值人民币m张，10元面值人民币n张，共有人民币 元（用含m、n的代数式表示）．
12．一种商品每件成本价是元，按成本增加定价出售，后由于库存积压，又按定价的出售，则该商品现在的售价是 元.
13．一个两位数，二个数位上数字之和为，若个位上的数字为2，则这个两位数为 ．
14．有三个连续偶数，如果假设最大的一个偶数为n，则其余两个为 .
15．下列用字母表示数的写法中哪些不规范，请改正过来．
(1)3x＋1；(2)m×n－3；(3)2·y；(4)a·m＋b×n元；(5)a÷(b＋c)；(6)a－1÷b．
16．设某数为，用表示下列各数：
(1)某数与的差；
(2)某数的与的和；
(3)某数与1的差的平方；
(4)某数与2的和的倒数；
(5)某数的30%除以的商．
17．下列表述中，字母各表示什么？
(1)正方形的周长为4a；
(2)买单价为5元的毛巾，花了5a元钱；
(3)某班女生比男生多1人，女生共有（x+1）人．
18．体育委员小金带了500元钱去买体育用品，已知一个足球x元，一个篮球y元．则代数式表示的实际意义为？体育委员买了2个足球、3个篮球，剩余的经费？
能力提升
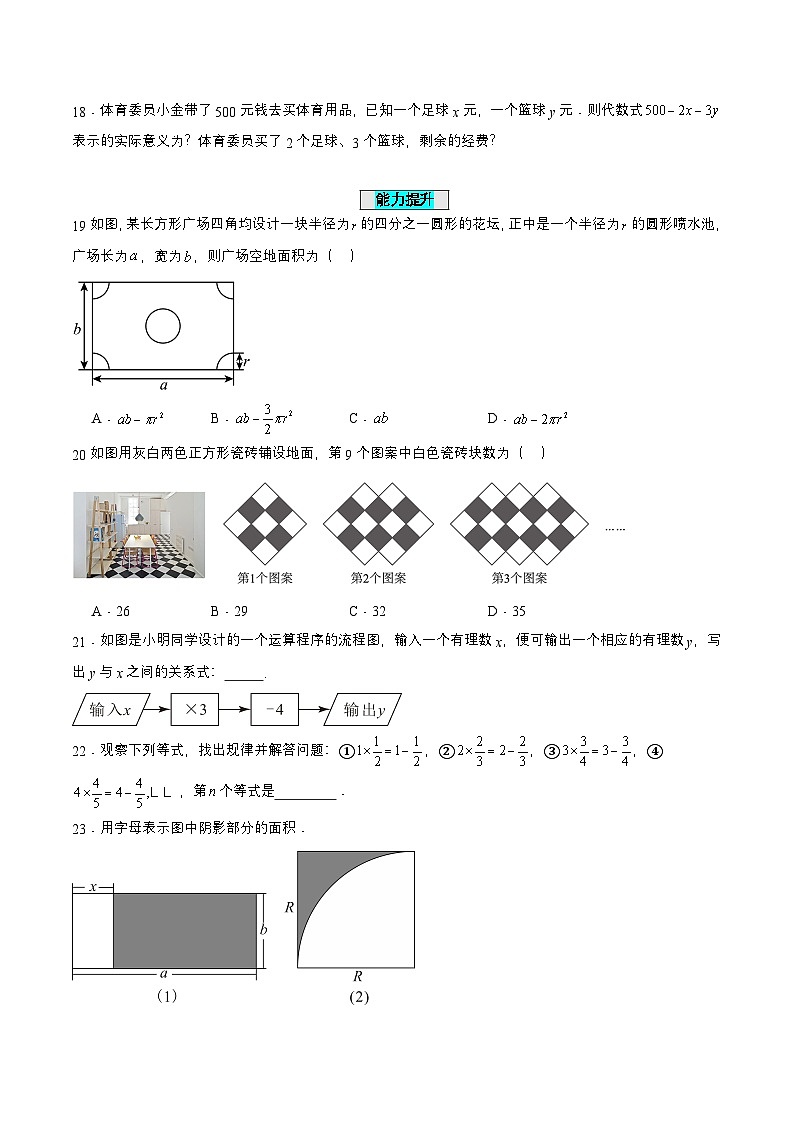
19如图，某长方形广场四角均设计一块半径为的四分之一圆形的花坛，正中是一个半径为的圆形喷水池，广场长为，宽为，则广场空地面积为（ ）

A．B．C．D．
20如图用灰白两色正方形瓷砖铺设地面，第9个图案中白色瓷砖块数为（ ）

A．26B．29C．32D．35
21．如图是小明同学设计的一个运算程序的流程图，输入一个有理数x，便可输出一个相应的有理数y，写出y与x之间的关系式： .

22．观察下列等式，找出规律并解答问题：①，②，③，④，第个等式是 ．
23．用字母表示图中阴影部分的面积．
拔高拓展
24．【材料阅读】高斯上小学时，有一次数学老师让同学们计算“从1到100这100个正整数的和”．许多同学都采用了依次累加的计算方法，计算起来非常繁琐，且易出错．聪明的高斯经过探索后，给出了下面的解答过程：
解：设，①
则．②
①＋②，得（即左右两边分别相加）：
．
所以，．
所以，．
后来人们将高斯的这种解答方法概括为“倒序相加法”．
【问题解决】利用“倒序相加法”解答下面的问题：
(1)计算：_________；
(2)猜想：__________并利用“倒序相加法”说明理由．
(3)利用（2）中的结论，计开：．
2.1.1 用字母表示数 分层作业
基础训练
1．下列各式中，符合代数式书写要求的是（ ）．
A．B．C．D．
【答案】D
【分析】根据代数式的书写规范，对各个选项逐个分析，即可得到答案．
【详解】解：应表示为：，故选项A不符合要求；
应表示为：，故选项B不符合要求；
应表示为：，故选项C不符合要求；
的书写规范，故选项D符合题意；
故选：D．
【点睛】本题考查了代数式的知识；解题的关键是熟练掌握代数式的书写规范，从而完成求解．
2．用代数式表示：“a，b两数的平方和与a，b乘积的差”，正确的是（ ）
A． B． C． D．
【答案】A
【分析】先求得a，b两数的平方和为，再减去a，b乘积列式得出答案即可．
【详解】解：“a，b两数的平方和与a，b乘积的差”，列示为，
故选：A．
【点睛】此题考查列代数式，找出题目蕴含的数量关系是解决问题的关键．
3．若表示一个两位数，也表示一个两位数，小明想用、来组成一个四位数，且把放在的左边，你认为下列表达式中哪一个是正确的（ ）
A．B．C．D．
【答案】C
【分析】根据题意，可知新的四位数中扩大了100倍，而没有变，从而可以用含、的代数式表示出这个四位数．
【详解】解：由题意可得新的四位数中扩大了100倍，而没有变，所以这个四位数是：，
故选C．
【点睛】本题考查了列代数式，解答本题的关键是明确题意，列出相应的代数式．
4．甲，乙两商场以相同的价格出售同样的商品，当购物金额超出一定数额后，各自推出不同的优惠方案，若在两个商场购买元的商品，在甲商场需付费元，在乙商场需付费元，下列关于两个商场优惠方案的说法正确的是（ ）
A．购买金额不超过100元时，两个商场都不优惠
B．购买金额超过50元时，两个商场都有优惠
C．购买金额超过100元时，甲商场按收费，乙商场按收费
D．购买金额超过100元时，超出100元的部分，甲商场按收费，乙商场按收费
【答案】D
【分析】根据代数式还原打折销售的方式即可得解．
【详解】解：∵甲商场需付费元，
∴甲商场付费时，100元以内不打折，超过超出100元的部分，甲商场按收费，
∵乙商场需付费元，
∴乙商场付费时，50元以内不打折，超过超出50元的部分，乙商场按收费，
∴乙商场付费时，超过超出100元的部分，乙商场按收费，
故选：D.
【点睛】此题考查了列代数式，读懂题意，明确打折销售是解题的关键．
5．如果设正方形纸的边长为acm，所折无盖长方体形盒子的高为hcm，用a与h来表示这个无盖长方体形盒子的容积是（ ）
A．B．C．D．
【答案】B
【分析】根据题意求得无盖长方体形盒子的长、宽、高，然后计算体积即可．
【详解】依题意得：（a-2h）（a-2h）•h=（a-2h）2•h（cm3） 故选B．
【点睛】考查了列代数式．找到关键描述语从而根据等量关系准确的列出函数关系式是解决问题的关键．
6．某商品原价为a元，先提高20%，然后连续两次降价，每次降价10%．则该商品的价格是（ ）
A．元B．元C．元D． 元
【答案】B
【分析】根据题目要求列出代数式化简计算即可．
【详解】依题意，该商品经过一次的升价，再经过两次的降价，目前的价格为：
．
故选：B．
【点睛】本题考查用字母表示数，较为简单；另外本题为选择题，在化简计算时可采用尾数判别法（即的结果应有三位小数且尾数是）可快速选出答案．
7．下列用字母表示数的式子中，符合书写要求的有 个．
，，，，，
【答案】1
【分析】根据代数式的书写要求分别进行判断即可．
【详解】解：用字母表示数的式子中，符合书写要求的有：，共有1个．
故答案为：1．
【点睛】本题主要考查了列代数式，用到的知识点是代数式的书写要求：
（1）在代数式中出现的乘号，通常简写成“”或者省略不写；
（2）数字与字母相乘时，数字要写在字母的前面；
（3）在代数式中出现的除法运算，一般按照分数的写法来写．带分数要写成假分数的形式．
8．用字母表示运算律：如果用a、b、c分别表示有理数，那么加法交换律可以表示成： ；加法结合律可以表成： ；乘法交换律可以表示成： ；乘法结合律可以表成： ；乘法对加法的分配律可以表示成： ．
【答案】
【解析】略
9．填空题
（1）某种足球元，则涨价20%后是 元；
（2）箱橘子重kg，每箱重 kg；
（3）购买单价为元的笔记本8本，共需人民币 元；
（4）小明的体重是kg，小红比小明重kg，则小红的体重是 kg；
（5）张师傅第一天生产个零件，第二天比第一天减少5%，第二天生产零件 个．
【答案】
【分析】（1）根据上涨的百分率可得涨价20%后可表示为，从而可得答案；
（2）由总重量除以总数量即可；
（3）由单价乘以数量可得答案；
（4）由小红的体重等于小明的体重加上比小明重的体重即可；
（5）根据减少的百分率可得第二天比第一天减少5%，可表示为，从而可得答案．
【详解】解：（1）某种足球元，则涨价20%后是元；
（2）箱橘子重kg，每箱重kg；
（3）购买单价为元的笔记本8本，共需人民币元；
（4）小明的体重是kg，小红比小明重kg，则小红的体重是kg；
（5）张师傅第一天生产个零件，第二天比第一天减少5%，第二天生产零件个．
故答案为：（1）；（2）；（3）；（4）；（5）
【点睛】本题考查的是列代数式，理解题意，注意语句中体现的运算顺序是解本题的关键．
10．某超市的苹果价格如图，试说明代数式100﹣9.8x的实际意义 ．
【答案】用100元买每斤9.8元的苹果x斤余下的钱
【分析】根据题意结合图片得出代数式100﹣9.8x的实际意义．
【详解】解：代数式100﹣9.8x的实际意义为：用100元买每斤9.8元的苹果x斤余下的钱．
故答案为：用100元买每斤9.8元的苹果x斤余下的钱．
【点睛】此题主要考查了代数式，结合题意利用图片得出是解题关键．
11．现有5元面值人民币m张，10元面值人民币n张，共有人民币 元（用含m、n的代数式表示）．
【答案】
【分析】由5元面值人民币m张，可得人民币元，由10元面值人民币n张，可得人民币元，从而可得答案．
【详解】解：由题意得：共有人民币元，
故答案为：
【点睛】本题考查的是列代数式，掌握列代数式的方法是解题的关键．
12．一种商品每件成本价是元，按成本增加定价出售，后由于库存积压，又按定价的出售，则该商品现在的售价是 元.
【答案】1.08a
【分析】先列出开始的售价，再列出后来的售价即可．
【详解】解：由题意可知，开始的售价为(1+20％)a元，
所以后来的售价为90％×(1+20％)a=1.08a元..
故答案为1.08a．
【点睛】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式．
13．一个两位数，二个数位上数字之和为，若个位上的数字为2，则这个两位数为 ．
【答案】10x-18．
【分析】根据数字的表示方法列式即可．
【详解】解：∵二个数位上数字之和为，个位上的数字为2
∴十位上的数为x-2
∴这个两位数是10（x-2）+2=10x-18．
故答案为10x-18．
【点睛】本题主要考查了数字的表示方法，用x表示出各数位上的数字是解答本题的关键．
14．有三个连续偶数，如果假设最大的一个偶数为n，则其余两个为 .
【答案】（n-2），（n-4）
【分析】理解相邻偶数差为2可得.
【详解】如果假设最大的一个偶数为n，
则其余2个应分别比它小2，小4，
依次是（n-2），（n-4）．
【点睛】考核知识点：整式.理解偶数性质是关键.
15．下列用字母表示数的写法中哪些不规范，请改正过来．
(1)3x＋1；(2)m×n－3；(3)2·y；(4)a·m＋b×n元；(5)a÷(b＋c)；(6)a－1÷b．
【答案】见解析
【分析】（1）根据数与字母相乘的规则判断即可；
（2）根据字母与字母相乘的规则判断即可；
（3）根据数与字母相乘的规则判断即可；
（4）根据字母与字母相乘的规则判断即可；
（5）根据除号一般用分数线表示的规则判断即可；
（6）根据除号一般用分数线表示的规则判断即可．
【详解】解：(1)3x＋1书写规范；
(2)m×n－3应该是mn－3；
(3)2·y应该是2y；
(4)a·m＋b×n元应该是(am＋bn)元；
(5)a÷(b＋c)应该是 ；
(6)a－1÷b应该是a－．
【点睛】本题主要考查代数式的书写，掌握代数式的书写要求是解题的关键．
16．设某数为，用表示下列各数：
(1)某数与的差；
(2)某数的与的和；
(3)某数与1的差的平方；
(4)某数与2的和的倒数；
(5)某数的30%除以的商．
【答案】(1)
(2)
(3)
(4)
(5)
【分析】（1）根据语句的含义列出代数式即可；
（2）先表示某数的，再求和列出代数式即可；
（3）先表示差，再表示差的平方，再列式即可；
（4）先表示和，再表示和的倒数即可；
（5）先表示某数的30%，再表示商即可．
【详解】（1）解：某数与的差表示为：；
（2）某数的与的和表示为：；
（3）某数与1的差的平方表示为：；
（4）某数与2的和的倒数表示为：；
（5）某数的30%除以的商表示为：．
【点睛】本题考查的是列代数式，理解语句中的运算顺序是解本题的关键．
17．下列表述中，字母各表示什么？
(1)正方形的周长为4a；
(2)买单价为5元的毛巾，花了5a元钱；
(3)某班女生比男生多1人，女生共有（x+1）人．
【答案】(1)a表示正方形的边长
(2)a表示毛巾的数量
(3)x表示男生的人数
【分析】（1）根据正方形的周长＝边长×4即可得出答案；
（2）根据总价＝单价×数量即可得出答案；
（3）根据女生比男生多1人即可得出答案．
【详解】（1）解：根据题意可得，a表示正方形的边长；
（2）解：根据题意可得，a表示毛巾的数量；
（3）解：根据题意可得，x表示男生的人数．
【点睛】本题考查了代数式，熟练掌握各代数式的意义是解题的关键．
18．体育委员小金带了500元钱去买体育用品，已知一个足球x元，一个篮球y元．则代数式表示的实际意义为？体育委员买了2个足球、3个篮球，剩余的经费？
【答案】表示体育委员小金买了2个足球、3个篮球后，剩余的经费；元
【分析】根据代数式结合一个足球x元，一个篮球y元得出代数式表示的意义即可；根据体育委员买了2个足球、3个篮球，列出代数式即可．
【详解】解：∵体育委员小金带了500元钱去买体育用品，一个足球x元，一个篮球y元，
∴表示体育委员小金买了2个足球、3个篮球后，剩余的经费；
体育委员买了2个足球、3个篮球，剩余的经费为元．
【点睛】本题主要考查了代数式表示的实际意义，列代数式，解题的关键是理解题意．
能力提升
19如图，某长方形广场四角均设计一块半径为的四分之一圆形的花坛，正中是一个半径为的圆形喷水池，广场长为，宽为，则广场空地面积为（ ）

A．B．C．D．
【答案】D
【分析】分别求出广场的面积，草地面积，喷水池面积，用广场面积减去草地和喷水池的面积即可得出答案．
【详解】解：广场的面积为，
草地的面积为：，
喷水池的面积为：，
则广场空地面积为：，
故选：．
【点睛】本题考查了列代数式，掌握四个花坛的面积正好是一个圆的面积是解答本题的关键．
20如图用灰白两色正方形瓷砖铺设地面，第9个图案中白色瓷砖块数为（ ）
A．26B．29C．32D．35
【答案】B
【分析】观察图形，找出规律是此类题目的关键．
【详解】解：观察图形的变化可知：
第1个图案中白色瓷砖块数为；
第2个图案中白色瓷砖块数为；
第3个图案中白色瓷砖块数为；
依此类推，
第n个图案中，白色瓷砖是，
∴第9个图案中白色瓷砖块数为
故选：B．
【点睛】本题考查图形的规律问题，此类题找规律的时候，一定要结合图形进行分析，注意前后两个图形之间的联系．
21．如图是小明同学设计的一个运算程序的流程图，输入一个有理数x，便可输出一个相应的有理数y，写出y与x之间的关系式： .

【答案】
【分析】根据运算程序式列出y与x之间的关系式即可．
【详解】解：由运算程序得，
故答案为：．
【点睛】本题主要考查了程序运算式，解题的关键是理解题意，根据运算程序列出代数式．
22．观察下列等式，找出规律并解答问题：①，②，③，④，第个等式是 ．
【答案】
【分析】根据已知等式中的分子与分母的变化规律，进而得出答案即可．
【详解】，
，
，
，
……
∴第个等式为．
故答案为：．
【点睛】本题主要考查了数字的变化规律，根据已知得出数据中变与不变从而得出规律是解题关键．
23．用字母表示图中阴影部分的面积．
【答案】（1）ab﹣bx；（2）R2πR2
【分析】（1）读图可得，阴影部分的面积＝大长方形的面积﹣小长方形的面积；
（2）阴影部分的面积＝正方形的面积﹣扇形的面积．
【详解】解：（1）阴影部分的面积＝ab﹣bx；
（2）阴影部分的面积＝R2πR2．
【点睛】本题考查代数式的应用，解决问题的关键是看懂图，找到所求的阴影部分的面积和各部分之间的等量关系．
拔高拓展
24．【材料阅读】高斯上小学时，有一次数学老师让同学们计算“从1到100这100个正整数的和”．许多同学都采用了依次累加的计算方法，计算起来非常繁琐，且易出错．聪明的高斯经过探索后，给出了下面的解答过程：
解：设，①
则．②
①＋②，得（即左右两边分别相加）：
．
所以，．
所以，．
后来人们将高斯的这种解答方法概括为“倒序相加法”．
【问题解决】利用“倒序相加法”解答下面的问题：
(1)计算：_________；
(2)猜想：__________并利用“倒序相加法”说明理由．
(3)利用（2）中的结论，计开：．
【答案】(1)
(2)
(3)
【分析】（1）根据题目中的例子可以求得所求式子的值；
（2）根据题目中的例子，可以写出猜想的结果；
（3）根据（2）中结论即可得到结果．
【详解】（1）解：设①
则②
①+②，．
所以，，
所以，，
故答案为：；
（2）解：解：设①
则②
①+②，．
猜想：，
故答案为：；
（3）解：．
【点睛】本题考查数字的变化类、有理数的混合运算，解答本题的关键是明确题意，发现题目中数字的变化特点，求出所求式子的值．