

所属成套资源:人教版八年级数学上册重难考点专练特训(原卷版+解析)
人教版八年级数学上册重难考点专题01与三角形有关的线段(知识串讲+10大考点)特训(原卷版+解析)
展开
这是一份人教版八年级数学上册重难考点专题01与三角形有关的线段(知识串讲+10大考点)特训(原卷版+解析),共62页。
知识串讲
(一)三角形的概念
三角形的概念:由不在同一条直线上的三条线段首尾依次相接所组成的图形叫做三角形。
三角形特性
三角形用符号“”表示,顶点是A、B、C的三角形记作“ABC”,读作“三角形ABC”。
(二)三角形的分类
三角形按边的关系分类如下:
三角形按角的关系分类如下:
(三)三角形的稳定性
三角形的稳定性
三角形具有稳定性
四边形及多边形不具有稳定性
要使多边形具有稳定性,方法是将多边形分成多个三角形,这样多边形就具有稳定性了。
(四)三角形的三边关系
三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边
(1)三角形三边长分别是a,b,c,则a+b>c或c-b<a。
(2)已知三角形两边的长度分别为a,b,求第三边长度的范围:|a-b|<c<a+b
(五)三角形的相关线段
(1)①高线概念:从三角形一个顶点向它的对边做垂线,顶点和垂足之间的线段叫做三角形的高线(简称三角形的高)。
②高线性质:利用两个锐角互余(等量代换);利用等面积法求线段长度
(2)①中线概念:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线。
②中线性质:线段中点性质求线段相等;三角形的中线可以将三角形分为面积相等的两个小三角形
(3)①角平分线概念:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线
②角平分线性质:角度相等求解角度
考点训练
考点1:三角形的识别与相关概念
典例1:(2022秋·山东济宁·八年级校考阶段练习)如图,D是△ABC的边BC上的一点,则在△ABC中,∠C所对的边是_____;在△ACD中,∠C所对的边是_____.
【变式1】(2022·全国·八年级专题练习)如图,在△BCE中,边BE所对的角是________,∠CBE所对的边是________;在△AEC中,边AE所对的角是________,∠A为内角的三角形是________.
【变式2】(2022·全国·八年级专题练习)如图所示,顶点是A、B、C的三角形,记作___________,读作___________.其中,顶点A所对的边为___________还可用___________表示;顶点B所对的边为___________还可用___________表示;顶点C所对的边为___________还可用___________表示.
【变式3】(2021·八年级课前预习)由不在同一直线上的三条线段_______________所组成的图形叫做三角形.
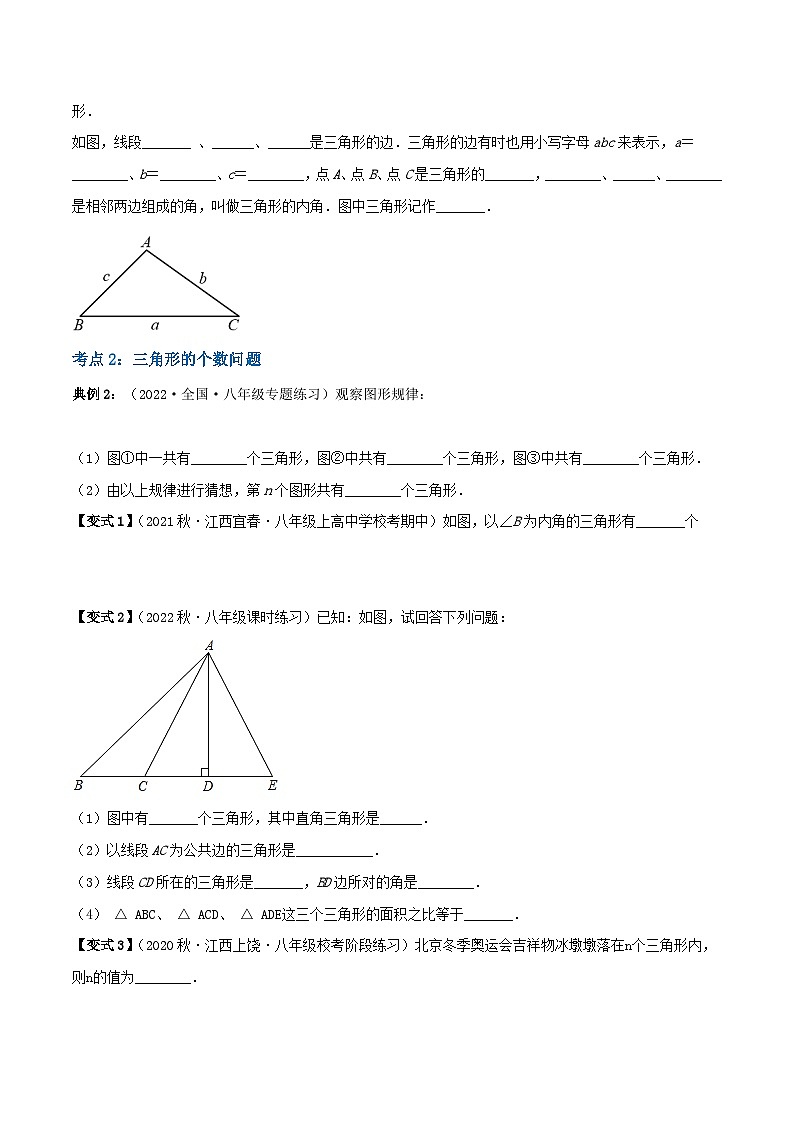
如图,线段_______ 、______、______是三角形的边.三角形的边有时也用小写字母abc来表示,a=________、b=________、c=________,点A、点B、点C是三角形的_______,________、______、________是相邻两边组成的角,叫做三角形的内角.图中三角形记作_______.
考点2:三角形的个数问题
典例2:(2022·全国·八年级专题练习)观察图形规律:
(1)图①中一共有________个三角形,图②中共有________个三角形,图③中共有________个三角形.
(2)由以上规律进行猜想,第n个图形共有________个三角形.
【变式1】(2021秋·江西宜春·八年级上高中学校考期中)如图,以∠B为内角的三角形有_______个
【变式2】(2022秋·八年级课时练习)已知:如图,试回答下列问题:
(1)图中有_______个三角形,其中直角三角形是______.
(2)以线段AC为公共边的三角形是___________.
(3)线段CD所在的三角形是_______,BD边所对的角是________.
(4)△ABC、△ACD、△ADE这三个三角形的面积之比等于_______.
【变式3】(2020秋·江西上饶·八年级校考阶段练习)北京冬季奥运会吉祥物冰墩墩落在n个三角形内,则n的值为________.
考点3:三角形的分类
典例3:(2022春·上海·七年级专题练习)在△ABC中,∠A=20°,∠B=60°,∠C=100°,那么△ABC是______三角形.(填“锐角”、“钝角”或“直角” )
【变式1】(2022秋·八年级课时练习)在ΔABC中,若∠A:∠B:∠C=3:5:7,则该三角形是_________三角形.(填“锐角”“直角”或“钝角”)
【变式2】(2022秋·八年级课时练习)已知a,b,c为三个正整数,如果a+b+c=12,那么以a,b,c为边能组成的三角形是:①等腰三角形,②等边三角形,③直角三角形,④钝角三角形.以上结论正确的是______.(只填序号)
【变式3】(2020·全国·七年级假期作业)观察图中的三角形,把它们的标号填入相应横线上.
锐角三角形_______,直角三角形________,钝角三角形________.
考点4:三角形的三边关系
典例4:(2021秋·甘肃武威·八年级校考阶段练习)若a,b,c是△ABC的三边的长,则化简|a−b−c|+|b−c−a|+|a+b−c|=________.
【变式1】(2023春·七年级课时练习)若等腰三角形的两边的长分别是5cm、7cm,则它的周长为___________cm.
【变式2】(2022秋·全国·八年级专题练习)已知三角形三边长分别为2,9,x,若x为偶数,则这样的三角形有___________个.
【变式3】(2022秋·广东广州·八年级校考阶段练习)已知△ABC的三边长分别为a,b,c,且a,b满足(a−1)2+b−2=0,则c 的取值范围是______.
考点5:三角形三边关系的应用
典例5:(2022秋·浙江·八年级专题练习)一个三角形的三边长均为整数.已知其中两边长为3和5,第三边长x是不等式组x−1⩽23x+25x−7>2x+13的正整数解.则第三边的长为:______.
【变式1】(2022秋·广东深圳·七年级统考期末)边长为1的小正方形组成如图所示的6×6网格,点A,B,C,D,E,F,G,H都在格点上.其中到四边形ABCD四个顶点距离之和最小的点是_________.
【变式2】(2022秋·八年级课时练习)如图,加油站A和商店B在马路MN的同一侧,A到MN的距离大于B到MN的距离,AB=700米.一个行人P在马路MN上行走,当P到A的距离与P到B的距离之差最大时,这个差等于______米.
【变式3】(2021秋·黑龙江佳木斯·八年级校联考期中)如图,填空:
由三角形两边的和大于第三边,得
AB+AD>____________,
PD+CD>____________.
将不等式左边、右边分别相加,得
AB+AD+PD+CD>__________,
即AB+AC>_________________.
考点6:与三角形高线有关的计算问题
典例6:(2023春·江苏盐城·七年级滨海县第一初级中学校考期中)如图,AD 是△ABC 的中线,BE 是△ABD 的中线, EF BC 于点 F.若S△ABC=24,BD 4 ,则 EF 长为___________.
【变式1】(2022秋·全国·八年级专题练习)如图,△ADF中,点B,C分别在AD,AF上,DC与BF交于点E,若DE:CE=2:1,S△DEF=6,S△DBE=4,则△ABC的面积=______.
【变式2】(2022秋·福建厦门·八年级厦门市槟榔中学校考期末)如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为___________.
【变式3】(2023秋·湖南邵阳·八年级统考期末)如图,在△ABC中,AB=AC=2,P是BC边上的任意一点,PE⊥AB于点E,PF⊥AC于点F.若S△ABC=2,则PE+PF=______.
考点7:三角形稳定性
典例7:(2022秋·云南昆明·八年级云大附中校考期中)随着人们物质生活的提高,手机成为一种生活中不可缺少的东西,手机很方便携带,但唯一的缺点就是没有固定的支点.为了解决这一问题,某工厂研制生产了一种如图所示的手机支架.把手机放在上面就可以方便地使用手机,这是利用了三角形的______.
【变式1】(2022秋·八年级课时练习)如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上 _____根木条.
【变式2】(2019·全国·八年级统考假期作业)下列图中哪些具有稳定性?________.
【变式3】(2023春·江苏扬州·七年级校联考阶段练习)如图,学校门口设置的移动拒马都用钢管焊接成三角形,这样做的数学原理是利用了三角形的_____(选填“稳定性”或“不稳定性”).
考点8:与三角形角平分线有关的计算问题
典例8:(2023春·七年级课时练习)如图所示,△ABC的两条角平分线相交于点D,过点D作EF∥BC,交AB于点E,交AC于点F,若△AEF的周长为30cm,则AB+AC=______cm.
【变式1】(2022秋·海南省直辖县级单位·八年级统考期末)如图,(1)若AM是△ABC的中线,BC=12cm,则BM=CM=______cm;
(2)若AD是△ABC的角平分线,则∠BAD=∠DAC=______;若∠BAC=106°,则∠DAC=______;
(3)若AH是△ABC的高,则△ABH是______三角形.
【变式2】(2022春·山东菏泽·七年级校联考阶段练习)如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.CF⊥AD于H,交AB于F.下列说法:①线段AG是△ABE的角平分线;②线段AE是△ABG的边BG上的高;③BG是△ABD的中线;④△ABG与△DBG的面积相等;⑤∠1+∠ACF=90°.其中正确的有______ (填序号).
【变式3】(2020秋·八年级课时练习)△ABC中,D为BC边上任意一点,DE、DF分别是△ADB和△ADC的角平分线,连接EF,则△DEF的形状为_________.
考点9:与三角形中线有关的周长、面积问题
典例9:(2022秋·浙江宁波·八年级统考阶段练习)如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为12,则△BCD的周长是_____.
【变式1】(2022秋·福建厦门·八年级统考期末)如图,S△ABD=S△ACD,已知AB=8cm,AC=5cm,那么△ABD和△ACD的周长差是________cm.
【变式2】(2023秋·广东广州·八年级统考期末)如图,BE是△ABC的中线,点D是BC边上一点,BD=2CD,BE、AD交于点F,若△ABC的面积为24,则S△BDF﹣S△AEF等于_____.
【变式3】(2022春·江苏泰州·七年级校联考期中)已知在ΔABC中,已知点D、E、F分别为BC、AD、CE的中点,且SΔBEF=4cm2,则SΔABC的值为______cm2.
考点10:利用网格求三角形的面积
典例10:(2023秋·福建龙岩·八年级校考期末)如图所示的正方形网格,A、B、C、D是网格线交点,则△ABC的面积与△ABD的面积的大小关系为:S△ABC ______S△ABD.填“>”、“=”或“AC,BC+CA>AB,CA+AB>BC.
18.(2022秋·河北廊坊·八年级校考期末)画图并填空:如图,方格纸中每个小正方形的边长都为1,△ABC的顶点都在方格纸的格点上,将△ABC经过一次平移,使点C移到点C'的位置.
(1)请画出△A'B'C';
(2)连接AA'、BB',则这两条线段的关系是______;
(3)在方格纸中,画出△ABC的中线BD和高CE.
19.(2021春·河北石家庄·七年级石家庄市第十九中学校考期末)(1)如图1,直线a∥直线b,点A、D在直线a上,点B、C在直线b上,连接AB、AC、BD、DC,得△ABC和△BDC,△ABC的面积_______△BDC的面积(填“>”、“=”或“<”).
(2)如图2,已知△ABC,过点A有一条线段,将△ABC的面积平分,且交BC于点D,则BDBC= .
(3)如图3,已知四边形ABCD,请过点D作一条线段DG将四边形ABCD面积平分.
20.(2023春·七年级单元测试)△ABC在如图所示的平面直角中,将其平移后得△A'B'C',若B的对应点B'的坐标是−2,2.
(1)在图中画出△A'B'C';
(2)此次平移可看作将△ABC向____平移了______个单位长度,再向____平移了______个单位长度得△A'B'C';
(3)△ABC的面积为______.
21.(2023·陕西西安·校考三模)已知:a、b、c满足(a−8)2+b−5+|c−32|=0求:
(1)a、b、c的值;
(2)试问以a、b、c为边能否构成三角形?若能构成三角形,求出三角形的周长;若不能构成三角形,请说明理由.
22.(2022春·黑龙江齐齐哈尔·七年级统考期中)在下列网格中建立平面直角坐标系,如图所示,每个小正方形的边长均为1个单位长度.已知A(1,1),B(3,4)和C(4,2).
(1)在图中标出点A,B,C;
(2)将点C向下平移3个单位到点D,将点A先向左平移3个单位,再向下平移1个单位到点E,在图中标出点D和点E;
(3)求△EBD的面积.
23.(2022春·福建福州·七年级福建省福州延安中学校考期末)若不等式组2x−a−3的解集是−1
相关试卷
这是一份专题01 图形的初步(1)(知识串讲+15大考点)-2024年中考数学总复习重难考点强化训练(全国通用),文件包含专题01图形的初步1知识串讲+15大考点全国通用原卷版docx、专题01图形的初步1知识串讲+15大考点全国通用解析版docx等2份试卷配套教学资源,其中试卷共68页, 欢迎下载使用。
这是一份专题01 统计(知识串讲+9大考点)-2024年中考数学总复习重难考点强化训练(全国通用),文件包含专题01统计知识串讲+9大考点全国通用原卷版docx、专题01统计知识串讲+9大考点全国通用解析版docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。
这是一份专题01 平移与轴对称(知识串讲+9大考点)-2024年中考数学总复习重难考点强化训练(全国通用),文件包含专题01平移与轴对称知识串讲+9大考点全国通用原卷版docx、专题01平移与轴对称知识串讲+9大考点全国通用解析版docx等2份试卷配套教学资源,其中试卷共56页, 欢迎下载使用。









