人教版八年级数学上册重难考点专题05最短路径问题(将军饮马)(知识串讲+4大考点)特训(原卷版+解析)

这是一份人教版八年级数学上册重难考点专题05最短路径问题(将军饮马)(知识串讲+4大考点)特训(原卷版+解析)，共40页。

知识串讲
（一）将军饮马模型
①两定一动
②一定两动
③两定两动
考点训练
考点1：两定一动
典例1：（2022秋·安徽池州·九年级统考期末）如图，Rt△ABC中，∠C=90°，AC=4，BC=3，点P为AC边上的动点，过点P作PD⊥AB于点D，则PB+PD的最小值为（ ）
A．154B．245C．5D．203
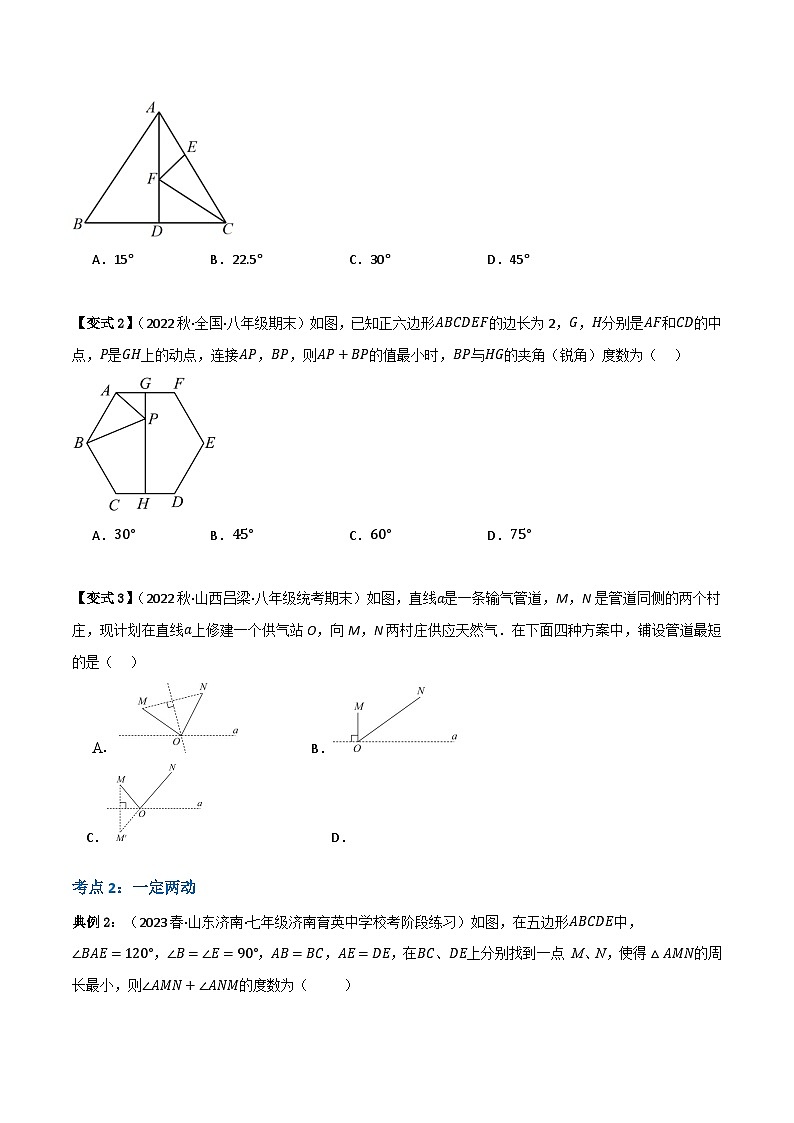
【变式1】（2023春·全国·七年级专题练习）如图，AD是等边△ABC的BC边上的中线，F是AD边上的动点，E是AC边上动点，当EF+CF取得最小值时，则∠ECF的度数为（ ）
A．15°B．22.5°C．30°D．45°
【变式2】（2022秋·全国·八年级期末）如图，已知正六边形ABCDEF的边长为2，G，H分别是AF和CD的中点，P是GH上的动点，连接AP，BP，则AP+BP的值最小时，BP与HG的夹角（锐角）度数为（ ）
A．30°B．45°C．60°D．75°
【变式3】（2022秋·山西吕梁·八年级统考期末）如图，直线a是一条输气管道，M，N是管道同侧的两个村庄，现计划在直线a上修建一个供气站O，向M，N两村庄供应天然气．在下面四种方案中，铺设管道最短的是（ ）
A． B．
C． D．
考点2：一定两动
典例2：（2023春·山东济南·七年级济南育英中学校考阶段练习）如图，在五边形ABCDE中，∠BAE=120°，∠B=∠E=90°，AB=BC，AE=DE，在BC、DE上分别找到一点 M、N，使得△AMN的周长最小，则∠AMN+∠ANM的度数为（ ）

A．100°B．110°C．120°D．130°
【变式1】（2019秋·内蒙古通辽·八年级校考期中）如图，OA,OB分别是线段MC,MD的垂直平分线，MD=5cm,MC=7cm,CD=10cm，一只小蚂蚁从点M出发爬到OA边上任意一点E，再爬到OB边上任意一点F，然后爬回M点，则小蚂蚁爬行的最短路径为（ ）
A．12cmB．10cmC．7cmD．5cm
【变式2】（2022·全国·八年级专题练习）如图，若∠AOB=44°，P为∠AOB内一定点，点M在OA上，点N在OB上，当△PMN的周长取最小值时，∠MPN的度数为( )
A．82°B．84°C．88°D．92°
【变式3】（2022秋·重庆·八年级重庆市育才中学校考阶段练习）如图所示，∠AOB＝60°，点P是∠AOB内一定点，并且OP＝2，点M、N分别是射线OA，OB上异于点O的动点，当△PMN的周长取最小值时，点O到线段MN的距离为（ ）
A．1B．2C．4D．1.5
考点3：两定两动
典例3：（2023·江苏·八年级假期作业）如图，在边长为8的正方形ABCD中，点G是BC边的中点，E、F分别是AD和CD边上的点，则四边形BEFG周长的最小值为______．
【变式1】（2022秋·全国·九年级专题练习）在长方形ABCD中，AB＝4，BC＝8，点P、Q为BC边上的两个动点（点P位于点Q的左侧，P、Q均不与顶点重合），PQ＝2
(1)如图①，若点E为CD边上的中点，当Q移动到BC边上的中点时，求证：AP＝QE；
(2)如图②，若点E为CD边上的中点，在PQ的移动过程中，若四边形APQE的周长最小时，求BP的长；
(3)如图③，若M、N分别为AD边和CD边上的两个动点（M、N均不与顶点重合），当BP＝3，且四边形PQNM的周长最小时，求此时四边形PQNM的面积．
考点4：造桥选址
典例4：（2023秋·七年级单元测试）如图，直线l1，l2表示一条河的两岸，且l1 ∥ l2．现要在这条河上建一座桥（桥与河的两岸相互垂直），使得从村庄P经桥过河到村庄Q的路程最短，应该选择路线（ ）
A．B．
C．D．
【变式1】（2023春·全国·七年级专题练习）已知村庄A和B分别在一条河的两岸，现要在河上造一座桥MN(假定河的两岸彼此平行，且桥与河岸互相垂直)，下列示意图中，桥的建造位置能使从村庄A经桥过河到村庄B的路程最短的是( )
A．B．
C．D．
【变式2】（2023春·全国·七年级专题练习）如图，平行河岸两侧各有一城镇P，Q，根据发展规划，要修建一条桥梁连接P，Q两镇，已知相同长度造桥总价远大于陆上公路造价，为了尽量减少总造价，应该选择方案（ ）
A． B．
C． D．
同步过关
一、单选题
1．（2022秋·八年级课时练习）如图，在△ABC中，点E、D分别在AB、AC的延长线上，∠BAC与∠CBE的平分线相交于点P，BE=BC，PB与CE交于点H，PG∥DA交BC于F，交AB于G，下列结论：①GA=GP；②CP平分∠BCD；③BP垂直平分CE，其中正确的结论有（ ）
A．0个B．1个C．2个D．3个
2．（2023·山东潍坊·统考模拟预测）如图，等腰三角形ABC的底边BC长为6，腰AC的垂直平分线EF分别交边AC、AB于点E，F，若D为BC边的中点，M为线段EF上一动点，若三角形CDM的周长的最小值为13，则等腰三角形ABC的面积为（ ）
A．78B．39C．42D．30
3．（2023秋·广东江门·八年级统考期中）如图，Rt△ABC中，∠ACB=90°，AC=6,BC=8,AB=10，BD平分∠ABC，如果M、N分别为BD、BC上的动点，那么CM+MN的最小值是（ ）
A．2.4B．3C．4D．4.8
4．（2022秋·八年级单元测试）如图所示，∠AOB＝60°，点P是∠AOB内一定点，并且OP＝2，点M、N分别是射线OA，OB上异于点O的动点，当△PMN的周长取最小值时，点O到线段MN的距离为（ ）
A．1B．2C．4D．1.5
5．（2023春·山西晋中·七年级统考期中）如图，河道l的同侧有M、N两地，现要铺设一条引水管道，从P地把河水引向M、N两地．下列四种方案中，最节省材料的是（ ）
A．B．
C．D．
二、填空题
6．（2020秋·八年级课时练习）如图，在△ABC中，AB=3,AC=4,AB⊥AC,EF垂直平分BC，点P为直线EF上一动点，则△ABP周长的最小值是________．
7．（2022秋·江苏·八年级期末）如图，AD为等边△ABC的高，E、F分别为线段AD、AC上的动点，且AE＝CF，当BF＋CE取得最小值时，∠AFB＝_______°．
8．（2023秋·福建南平·八年级统考期末）如图，∠AOB=22°，点M，N分别是边OA，OB上的定点，点P，Q分别是边OA，OB上的动点，记∠MQP=α，∠OPN=β，当MQ+QP+PN最小时，则α与β的数量关系为____________．
三、解答题
9．（2023秋·吉林·七年级统考期末）如图，平面上有五个点A，B，C，D，E．按下列要求画出图形．
（1）连接BD；
（2）画直线AC交线段BD于点M；
（3）请在直线AC上确定一点N，使B，E两点到点N的距离之和最小．
10．（2022秋·内蒙古呼伦贝尔·九年级统考期末）如图，△ABC三个顶点的坐标分别为A(1，1)，B(4，2)，C(3，4)．
（1）请画出ΔABC关于原点对称的ΔA1B1C1；
（2）在x轴上求作一点P，使ΔPAB的周长最小，请画出ΔPAB，并直接写出P的坐标．
11．（2022秋·北京·八年级北京市第一六六中学校考期中）在直角坐标系中，△ABC的三个顶点的位置如图所示．
(1)请画出△ABC关于y轴对称的△A'B'C'（其中A'，B'，C'分别是A，B，C的对应点，不写画法）；
(2)直接写出A'，B'，C'三点的坐标：A'（ ），B'（ ），C'（ ）
(3)在x轴上找出点P，使得点P到点A、点B的距离之和最短（保留作图痕迹）
(4)点Q在坐标轴上，且满足△BCQ是等腰三角形，则所有符合条件的Q点有__________个．
专题05 最短路径问题（将军饮马）
考点类型
知识串讲
（一）将军饮马模型
①两定一动
②一定两动
③两定两动
考点训练
考点1：两定一动
典例1：（2022秋·安徽池州·九年级统考期末）如图，Rt△ABC中，∠C=90°，AC=4，BC=3，点P为AC边上的动点，过点P作PD⊥AB于点D，则PB+PD的最小值为（ ）
A．154B．245C．5D．203
【答案】B
【分析】作点B关于AC的对称点B'，过点B'作B'D⊥AB于点D，交AC于点P，点P即为所求作的点，此时PB+PD有最小值，连接AB'，根据对称性的性质，可知：BP=B'P，△ABC≅△AB'C，根据S△ABB'=S△ABC+S△AB'C=2S△ABC，即可求出PB+PD的最小值．
【详解】解：如下图，作点B关于AC的对称点B'，过点B'作B'D⊥AB于点D，交AC于点P，连接AB'，点P即为所求作的点，此时PB+PD有最小值，
根据对称性的性质，可知：BP=B'P，
在Rt△ABC中，∠ACB=90°,AC=4,BC=3，
∴AB=AC2+BC2=5，
根据对称性的性质，可知：△ABC≅△AB'C，
∴S△ABB'=S△ABC+S△AB'C=2S△ABC，
即12×AB⋅B'D=2×12BC⋅AC，
∴5B'D=24，
∴B'D=245，
故选：B．
【点睛】本题考查了轴对称一最短路线问题，解题的关键是掌握轴对称的性质．
【变式1】（2023春·全国·七年级专题练习）如图，AD是等边△ABC的BC边上的中线，F是AD边上的动点，E是AC边上动点，当EF+CF取得最小值时，则∠ECF的度数为（ ）
A．15°B．22.5°C．30°D．45°
【答案】C
【分析】过点B作BE⊥AC于点E，交AD于点F，连接CF，根据垂线段最短可知此时EF+CF取得最小值，再利用等边三角形的性质求解即可．
【详解】解：如图：
过点B作BE⊥AC于点E，交AD于点F，连接CF，
根据垂线段最短可知此时EF+CF取得最小值，
∵△ABC是等边三角形，
∴AE＝EC，
AF＝FC，
∴∠FAC＝∠FCA，
∵AD是等边△ABC的BC边上的中线，
∴∠BAD＝∠CAD＝30°，
∴∠ECF＝30°．
故选：C．
【点睛】本题考查最短路径问题——垂线段最短，等边三角形的性质，根据垂线段最短找到点E、F是解题的关键．
【变式2】（2022秋·全国·八年级期末）如图，已知正六边形ABCDEF的边长为2，G，H分别是AF和CD的中点，P是GH上的动点，连接AP，BP，则AP+BP的值最小时，BP与HG的夹角（锐角）度数为（ ）
A．30°B．45°C．60°D．75°
【答案】C
【分析】连接PF，BF，BF交GH于点P'，连接AP'，首先证明当点P与点P'重合时，PA+PB的最小值，利用等腰三角形的性质求出∠AFB=30°即可解决问题．
【详解】解：如图，连接PF，BF，BF交GH于点P'，连接AP'．
∵正六边形ABCDEF中，G，H分别是AF和CD的中点，
∴GH所在直线是正六边形的对称轴，
∴PA=PF，
∴PA+PB=PB+PF，
∵PB+PF⩾BF，
∴当点P与点P'重合时，PA+PB的值最小，
∵∠BAF=120°，AB=AF，
∴∠ABF=∠AFB=30°，
∵∠FGP'=90°，
∴∠FP'G=60°，
故选：C．
【点睛】本题考查正多边形与轴对称的最短问题等知识，解题的关键是学会利用三角形的性质以及三边关系解决最短问题，属于中考常考题型．
【变式3】（2022秋·山西吕梁·八年级统考期末）如图，直线a是一条输气管道，M，N是管道同侧的两个村庄，现计划在直线a上修建一个供气站O，向M，N两村庄供应天然气．在下面四种方案中，铺设管道最短的是（ ）
B．
C． D．
【答案】C
【分析】利用对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离．
【详解】解：作点M关于直线a的对称点M'，连接M'N交直线a于O．
根据两点之间，线段最短，可知选项C修建的管道，则所需管道最短．
故选：C．
【点睛】本题考查了最短路径的数学问题．这类问题的解答依据是“两点之间，线段最短”．由于所给的条件的不同，解决方法和策略上又有所差别．
考点2：一定两动
典例2：（2023春·山东济南·七年级济南育英中学校考阶段练习）如图，在五边形ABCDE中，∠BAE=120°，∠B=∠E=90°，AB=BC，AE=DE，在BC、DE上分别找到一点 M、N，使得△AMN的周长最小，则∠AMN+∠ANM的度数为（ ）

A．100°B．110°C．120°D．130°
【答案】C
【分析】根据要使△AMN的周长最小，即利用点的对称，让三角形的三边在同一直线上，A关于BC和ED的对称点A'，A''，即可得出∠A'+∠A''=∠HAA'=60°，进而得出∠AMN+∠ANM=2∠A'+∠A''即可得出答案．
【详解】解：作A关于BC和ED的对称点A'，A''，连接A'，A''，交BC于M，交ED于N，则A'，A''即为△AMN的周长最小值．作EA延长线AH，

∵∠BAE=120°，
∴∠HAA'=60°，
∴∠A'+∠A''=∠HAA'=60°，
∵∠A'=∠MAA'，∠A''=∠NAE，
且∠A'+∠MAA'=∠AMN，∠A''+∠NAE=∠ANM，
∴∠A'+∠MAA'+∠NAE+∠A''=∠AMN+∠ANM=2∠A'+∠A''=2×60°=120°，
故选：C．
【点睛】此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识，根据已知得出M，N的位置是解题关键．
【变式1】（2019秋·内蒙古通辽·八年级校考期中）如图，OA,OB分别是线段MC,MD的垂直平分线，MD=5cm,MC=7cm,CD=10cm，一只小蚂蚁从点M出发爬到OA边上任意一点E，再爬到OB边上任意一点F，然后爬回M点，则小蚂蚁爬行的最短路径为（ ）
A．12cmB．10cmC．7cmD．5cm
【答案】B
【分析】由题意可知CD与OA的交点为E，与OB的交点为F，根据垂直平分线的性质计算即可；
【详解】由题意可知CD与OA的交点为E，与OB的交点为F．
∵OA,OB分别是线段MC,MD的垂直平分线，
∴ME=CE,MF=DF，
∴小蚂蚁爬行的最短路径为ME+EF+FM=CE+EF+FD=CD=10cm．
【点睛】本题主要考查了最短路线问题和垂直平分线的性质，准确计算是解题的关键．
【变式2】（2022·全国·八年级专题练习）如图，若∠AOB=44°，P为∠AOB内一定点，点M在OA上，点N在OB上，当△PMN的周长取最小值时，∠MPN的度数为( )
A．82°B．84°C．88°D．92°
【答案】D
【分析】分别作点P关于OA、OB的对称点P1、P2，连接P1P2交OA于M，交OB于N，△PMN的周长的最小值为P1P2长度，然后依据等腰等腰△OP1P2中，∠OP1P2+∠OP2P1=180°−2∠AOB，即可得出∠MPN=180°−2∠AOB，代入求解即可．
【详解】解：如图所示：分别作点P关于OA、OB的对称点P1、P2，连接P1P2交OA于M，交OB于N，
∴OP1=OP=OP2，∠OP1M=∠MPO，∠NPO=∠NP2O，
根据轴对称的性质可得MP=P1M，PN=P2N，
∴△PMN的周长的最小值为P1P2长度，
由轴对称的性质可得∠P1OP2=2∠AOB，
∴等腰△OP1P2中，
∠OP1P2+∠OP2P1=180°−∠P1OP2=180°−2∠AOB，
∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N
=∠OP1P2+∠OP2P1，
=180°−2∠AOB，
=92°，
故选：D．
【点睛】本题考查了轴对称-最短路线问题，轴对称的性质，等腰三角形的性质等，正确作出辅助线，综合运用这些知识点是解题关键．
【变式3】（2022秋·重庆·八年级重庆市育才中学校考阶段练习）如图所示，∠AOB＝60°，点P是∠AOB内一定点，并且OP＝2，点M、N分别是射线OA，OB上异于点O的动点，当△PMN的周长取最小值时，点O到线段MN的距离为（ ）
A．1B．2C．4D．1.5
【答案】A
【分析】分别作点P关于OB和OA的对称点P'和P″，连接OP'、OP″、P'P″，则P'P″与OB的交点为点N'，P'P″与OA的交点为点M'，连接PN'、PM'，则此时P'P″的值即为△PMN的周长的最小值，过点O作OC⊥P'P″于点C，求得∠OP'P″的值，由含30°角的直角三角形的性质可得答案．
【详解】解：分别作点P关于OB和OA的对称点P'和P″，连接OP'、OP″、P'P″，则P'P″与OB的交点为点N'，P'P″与OA的交点为点M'，连接PN'、PM'，则此时P'P″的值即为△PMN的周长的最小值，过点O作OC⊥P'P″于点C，如图所示：
由对称性可知OP＝OP'＝OP″＝2，
∵∠AOB＝60°，
∴∠P'O P″＝2×60°＝120°，
∴∠OP'P''＝∠OP'' P'＝30°，
∵OP＝2，OC⊥P'P″，
∴OC＝12OP'＝1；
故选：A．
【点睛】本题考查了轴对称-最短路线问题，熟练掌握轴对称的性质、等腰三角形的性质及含30°角的直角三角形的性质是解题的关键．
考点3：两定两动
典例3：（2023·江苏·八年级假期作业）如图，在边长为8的正方形ABCD中，点G是BC边的中点，E、F分别是AD和CD边上的点，则四边形BEFG周长的最小值为______．
【答案】24
【分析】作点G关于CD的对称点G'，作点B关于AD的对称点B'，连接B'G'、B'E、FG'，根据对称的性质可得BE=B'E，FG=FG'，再由BE+EF+FG+BG=B'E+EF+FG'+BG，B'E+EF+FG'≥B'G'，可得当B'E+EF+FG'=B'G'时，四边形BEFG的周长有最小值，最小值为BG+B'G'，再利用勾股定理求得B'G'=20，最后利用BG+B'G'即可求解．
【详解】解：如图，作点G关于CD的对称点G'，作点B关于AD的对称点B'，连接B'G'、B'E、FG'，
∵BE=B'E，FG=FG'，
∴BE+EF+FG+BG=B'E+EF+FG'+BG，
∵B'E+EF+FG'≥B'G'，
∴当B'E+EF+FG'=B'G'时，四边形BEFG的周长有最小值，最小值为BG+B'G'，
∵BG=CG=CG'=12BC=4，AB'=AB=8，
∴BB'=AB+AB'=16，BG'=BC+CG'=8+4=12，
∴B'G'=BG'2+BB'2=122+162=20，
∴BG+B'G'=4+20=24，
∴四边形BEFG的周长的最小值为24，
故答案为：24．
【点睛】本题考查了正方形的性质、轴对称的性质、勾股定理，三角形的三边关系，熟练掌握轴对称的性质，构造三角形是解题的关键．
【变式1】（2022秋·全国·九年级专题练习）在长方形ABCD中，AB＝4，BC＝8，点P、Q为BC边上的两个动点（点P位于点Q的左侧，P、Q均不与顶点重合），PQ＝2
(1)如图①，若点E为CD边上的中点，当Q移动到BC边上的中点时，求证：AP＝QE；
(2)如图②，若点E为CD边上的中点，在PQ的移动过程中，若四边形APQE的周长最小时，求BP的长；
(3)如图③，若M、N分别为AD边和CD边上的两个动点（M、N均不与顶点重合），当BP＝3，且四边形PQNM的周长最小时，求此时四边形PQNM的面积．
【答案】(1)见解析
(2)4
(3)4
【分析】（1）由“SAS”可证△ABP≌△QCE，可得AP=QE；
（2）要使四边形APQE的周长最小，由于AE与PQ都是定值，只需AP+EQ的值最小即可．为此，先在BC边上确定点P、Q的位置，可在AD上截取线段AF=DE=2，作F点关于BC的对称点G，连接EG与BC交于一点即为Q点，过A点作FQ的平行线交BC于一点，即为P点，则此时AP+EQ=EG最小，然后过G点作BC的平行线交DC的延长线于H点，那么先证明∠GEH=45°，再由CQ=EC即可求出BP的长度；
（3）要使四边形PQNM的周长最小，由于PQ是定值，只需PM+MN+QN的值最小即可，作点P关于AD的对称点F，作点Q关于CD的对称点H，连接FH，交AD于M，交CD于N，连接PM，QN，此时四边形PQNM的周长最小，由面积和差关系可求解．
【详解】（1）解：证明：∵四边形ABCD是矩形，
∴CD=AB=4，BC=AD=8，
∵点E是CD的中点，点Q是BC的中点，
∴BQ=CQ=4，CE=2，
∴AB=CQ，
∵PQ=2，
∴BP=2，
∴BP=CE，
又∵∠B=∠C=90°，
∴△ABP≌△QCE（SAS），
∴AP=QE；
（2）如图②，在AD上截取线段AF=PQ=2，作F点关于BC的对称点G，连接EG与BC交于一点即为Q点，过A点作FQ的平行线交BC于一点，即为P点，过G点作BC的平行线交DC的延长线于H点．
∵GH=DF=6，EH=2+4=6，∠H=90°，
∴∠GEH=45°，
∴∠CEQ=45°，
设BP=x，则CQ=BC-BP-PQ=8-x-2=6-x，
在△CQE中，∵∠QCE=90°，∠CEQ=45°，
∴CQ=EC，
∴6-x=2，
解得x=4，
∴BP=4；
（3）如图③，作点P关于AD的对称点F，作点Q关于CD的对称点H，连接FH，交AD于M，交CD于N，连接PM，QN，此时四边形PQNM的周长最小，连接FP交AD于T，
∴PT=FT=4，QC=BC-BP-PQ=8-3-2=3=CH，
∴PF=8，PH=8，
∴PF=PH，
又∵∠FPH=90°，
∴∠F=∠H=45°，
∵PF⊥AD，CD⊥QH，
∴∠F=∠TMF=45°，∠H=∠CNH=45°，
∴FT=TM=4，CN=CH=3，
∴四边形PQNM的面积=12×PF×PH-12×PF×TM-12×QH×CN=12×8×8-12×8×4-12×6×3=7．
【点睛】本题是四边形综合题，考查了矩形的性质，全等三角形的判定和性质，轴对称求最短距离，直角三角形的性质；通过构造平行四边形和轴对称找到点P和点Q位置是解题的关键．
考点4：造桥选址
典例4：（2023秋·七年级单元测试）如图，直线l1，l2表示一条河的两岸，且l1 ∥ l2．现要在这条河上建一座桥（桥与河的两岸相互垂直），使得从村庄P经桥过河到村庄Q的路程最短，应该选择路线（ ）
A．B．
C．D．
【答案】C
【分析】根据两点间直线距离最短，使EFP'P为平行四边形即可，即PP'垂直河岸且等于河宽，接连QP'即可．
【详解】解：作PP'垂直于河岸l2，使PP'等于河宽，
连接QP'，与另一条河岸相交于F，作FE⊥l1于点E，
则EF∥PP'且EF=PP'，
∴四边形EFP'P为平行四边形，
∴P'F=PE，
根据“两点之间线段最短”，QP'最短，即PF+FQ最短．
∴C选项符合题意，
故选：C．
【点睛】此题考查了轴对称-最短路径问题，解题的关键是利用“两点之间线段最短”．
【变式1】（2023春·全国·七年级专题练习）已知村庄A和B分别在一条河的两岸，现要在河上造一座桥MN(假定河的两岸彼此平行，且桥与河岸互相垂直)，下列示意图中，桥的建造位置能使从村庄A经桥过河到村庄B的路程最短的是( )
A．B．
C．D．
【答案】C
【分析】如图作AI∥MN，且AI=MN，连接BI，由两点之间线段最短可知此时从A点到B点的距离最短，所以AM∥BN.
【详解】
解：如图，作AI∥MN，且AI=MN，连接BI，
∴四边形AMNI为平行四边形，
∴AM∥BN，此时从A点到B点距离最短.
故选C.
【点睛】本题主要考查了最短路径的问题，运用到了两点之间线段最短，平行四边形等知识点，解此题的关键在于熟练掌握其知识点.
【变式2】（2023春·全国·七年级专题练习）如图，平行河岸两侧各有一城镇P，Q，根据发展规划，要修建一条桥梁连接P，Q两镇，已知相同长度造桥总价远大于陆上公路造价，为了尽量减少总造价，应该选择方案（ ）
A． B．
C． D．
【答案】C
【分析】作PP'垂直于河岸L，使PP′等于河宽，连接QP′，与河岸L相交于N，作NM⊥L，根据平行线的判定与性质，易证得此时PM+NQ最短.
【详解】解：如图，作PP'垂直于河岸L，使PP′等于河宽，连接QP′，与河岸L相交于N，作NM⊥L，则MN∥PP′且MN＝PP′，于是四边形PMNP′为平行四边形，故PM＝NP′．根据“两点之间线段最短”，QP′最短，即PM+NQ最短．观察选项，选项C符合题意．
故选C．
【点睛】本题主要考查最短路径问题，解此题的关键在于熟练掌握其知识点.
同步过关
一、单选题
1．（2022秋·八年级课时练习）如图，在△ABC中，点E、D分别在AB、AC的延长线上，∠BAC与∠CBE的平分线相交于点P，BE=BC，PB与CE交于点H，PG∥DA交BC于F，交AB于G，下列结论：①GA=GP；②CP平分∠BCD；③BP垂直平分CE，其中正确的结论有（ ）
A．0个B．1个C．2个D．3个
【答案】D
【分析】①根据角平分线的性质和平行线的性质进行判断；②根据角平分线的性质进行判断；③根据线段垂直平分线的性质进行判断即可．
【详解】解：①∵AP平分∠BAC，
∴∠CAP=∠BAP，
∵PG∥DA，
∴∠APG=∠CAP，
∴∠APG=∠BAP，
∴GA=GP，故①正确；
②如图，过点P作PM⊥BE于M，PN⊥AD于N，PQ⊥BC于Q，
∵∠BAC与∠CBE的平分线相交于点P，
∴PM=PN，PM=PQ，
∴PN=PQ，
∴点P也位于∠BCD的平分线上，
∴∠DCP=∠BCP，故②正确；
③∵BE=BC，BP平分∠CBE，
∴BP垂直平分CE（三线合一），故③正确；
故选：D．
【点睛】本题主要考查了角平分线的性质和定义，平行线的性质，等腰三角形的性质，熟练掌握各性质定理是解题的关键．
2．（2023·山东潍坊·统考模拟预测）如图，等腰三角形ABC的底边BC长为6，腰AC的垂直平分线EF分别交边AC、AB于点E，F，若D为BC边的中点，M为线段EF上一动点，若三角形CDM的周长的最小值为13，则等腰三角形ABC的面积为（ ）
A．78B．39C．42D．30
【答案】D
【分析】连接AD，由于△ABC是等腰三角形，点D是BC边的中点，可得AD⊥BC，再根据EF是线段AC的垂直平分线可知，点C关于直线EF的对称点为点A，故AD的长为CM+MD的最小值，再根据三角形的面积公式即可得出结论．
【详解】解：如图：连接AD，交EF于点M，
∵△ABC是等腰三角形，点D是BC边的中点，
∴AD⊥BC，CD=12BC=3，
∵EF是线段AC的垂直平分线，
∴点C关于直线EF的对称点为点A，AM=CM，
∴此时△CDM的周长最小，
∴CM+DM+CD=AM+DM+CD=AD+CD=13，
∴AD=13−CD=13−3=10，
∴S△ABC=12BC⋅AD=12×6×10=30，
故选：D．
【点睛】本题考查的是轴对称−最短路线问题，等腰三角形的性质，三角形的面积，熟知等腰三角形三线合一的性质是解答此题的关键．
3．（2023秋·广东江门·八年级统考期中）如图，Rt△ABC中，∠ACB=90°，AC=6,BC=8,AB=10，BD平分∠ABC，如果M、N分别为BD、BC上的动点，那么CM+MN的最小值是（ ）
A．2.4B．3C．4D．4.8
【答案】D
【分析】过点C作CE⊥AB于E，交BD于点M，过点M作MN⊥BC于点N，根据角平分线的性质定理得到ME=MN，进而得到CM+MN=CM+ME=CE，利用面积法求出CE=4.8，由此得到CM+MN的最小值．
【详解】解：过点C作CE⊥AB于E，交BD于点M，过点M作MN⊥BC于点N，
∵BD平分∠ABC，
∴ME=MN，
∴CM+MN=CM+ME=CE，
∵Rt△ABC中，∠ACB=90°，AC=6,BC=8,AB=10，CE⊥AB，
∵S△ABC=12AB⋅CE=12AC⋅BC，
∴10CE=6×8，
∴CE=4.8，即CM+MN的最小值是4.8
故选D．
【点睛】此题考查了角平分线的性质定理：角平分线上的点到角两边的距离相等，还考查了最短路线问题，解题的关键是找到使CM+MN最小时的动点N和M．
4．（2022秋·八年级单元测试）如图所示，∠AOB＝60°，点P是∠AOB内一定点，并且OP＝2，点M、N分别是射线OA，OB上异于点O的动点，当△PMN的周长取最小值时，点O到线段MN的距离为（ ）
A．1B．2C．4D．1.5
【答案】A
【分析】分别作点P关于OB和OA的对称点P'和P″，连接OP'、OP″、P'P″，则P'P″与OB的交点为点N'，P'P″与OA的交点为点M'，连接PN'、PM'，则此时P'P″的值即为△PMN的周长的最小值，过点O作OC⊥P'P″于点C，求得∠OP'P″的值，由含30°角的直角三角形的性质可得答案．
【详解】解：分别作点P关于OB和OA的对称点P'和P″，连接OP'、OP″、P'P″，则P'P″与OB的交点为点N'，P'P″与OA的交点为点M'，连接PN'、PM'，则此时P'P″的值即为△PMN的周长的最小值，过点O作OC⊥P'P″于点C，如图所示：
由对称性可知OP＝OP'＝OP″＝2，
∵∠AOB＝60°，
∴∠P'O P″＝2×60°＝120°，
∴∠OP'P''＝∠OP'' P'＝30°，
∵OP＝2，OC⊥P'P″，
∴OC＝12OP'＝1；
故选：A．
【点睛】本题考查了轴对称-最短路线问题，熟练掌握轴对称的性质、等腰三角形的性质及含30°角的直角三角形的性质是解题的关键．
5．（2023春·山西晋中·七年级统考期中）如图，河道l的同侧有M、N两地，现要铺设一条引水管道，从P地把河水引向M、N两地．下列四种方案中，最节省材料的是（ ）
A．B．
C．D．
【答案】D
【分析】垂线段最短，指的是从直线外一点到这条直线所作的垂线段最短．它是相对于这点与直线上其他各点的连线而言．
【详解】解：依据垂线段最短，以及两点之间，线段最短，可得最节省材料的是：
故选：D．
【点睛】本题主要考查了垂线段最短的运用，实际问题中涉及线路最短问题时，其理论依据应从“两点之间，线段最短”和“垂线段最短”这两个中去选择．
二、填空题
6．（2020秋·八年级课时练习）如图，在△ABC中，AB=3,AC=4,AB⊥AC,EF垂直平分BC，点P为直线EF上一动点，则△ABP周长的最小值是________．
【答案】7
【分析】根据题意知点B关于直线EF的对称点为点C，故当点P与点D重合时，AP+BP的最小值，求出AC长度即可得到结论．
【详解】解：∵EF垂直平分BC，
∴B，C关于直线EF对称．设AC交EF于点D，
∴当P和D重合时，AP+BP的值最小，最小值等于AC的长，
∴△ABP周长的最小值是4+3=7．
【点睛】本题考查了勾股定理，轴对称-最短路线问题的应用，解题的关键是找出P的位置．
7．（2022秋·江苏·八年级期末）如图，AD为等边△ABC的高，E、F分别为线段AD、AC上的动点，且AE＝CF，当BF＋CE取得最小值时，∠AFB＝_______°．
【答案】105°
【分析】如图，作辅助线，构建全等三角形，证明△AEC≌△CFH，得CE＝FH，将CE转化为FH，与BF在同一个三角形中，根据两点之间线段最短，确定点F的位置，即F为AC与BH的交点时，BF＋CE的值最小，求出此时∠AFB＝105°．
【详解】解：如图，作CH⊥BC，且CH＝BC，连接BH交AD于M，连接FH，
∵△ABC是等边三角形，AD⊥BC，
∴AC＝BC，∠DAC＝30°，
∴AC＝CH，
∵∠BCH＝90°，∠ACB＝60°，
∴∠ACH＝90°−60°＝30°，
∴∠DAC＝∠ACH＝30°，
∵AE＝CF，
∴△AEC≌△CFH，
∴CE＝FH，BF＋CE＝BF＋FH，
∴当F为AC与BH的交点时，BF＋CE的值最小，
此时∠FBC＝45°，∠FCB＝60°，
∴∠AFB＝105°，
故答案为105°.
【点睛】此题考查全等三角形的性质和判定、等边三角形的性质、最短路径问题，关键是作出辅助线，当BF＋CE取得最小值时确定点F的位置，有难度．
8．（2023秋·福建南平·八年级统考期末）如图，∠AOB=22°，点M，N分别是边OA，OB上的定点，点P，Q分别是边OA，OB上的动点，记∠MQP=α，∠OPN=β，当MQ+QP+PN最小时，则α与β的数量关系为____________．
【答案】β−α=44°
【分析】作M关于OB的对称点M'，N关于OA的对称点N'，连接M'N'交OA于P，交OB于Q，则MQ+QP+PN最小，易知∠OQM=∠OQM'=∠NQP，∠OPQ=∠APN'=∠APN，根据三角形的外角的性质和平角的定义即可得到结论．
【详解】解：如图，作M关于OB的对称点M'，N关于OA的对称点N'，连接M'N'交OA于P，交OB于Q，则MQ+QP+PN最小，
∴∠OQM=∠OQM'=∠NQP，∠OPQ=∠APN'=∠APN，
∴∠PQN=12180°−α=∠AOB+∠MPQ=22°+12180°−β，
∴β−α=44°，
故答案为：β−α=44°．
【点睛】本题考查轴对称—最短问题、三角形的内角和定理．三角形的外角的性质等知识，解题的关键是灵活运用所学知识解决问题．
三、解答题
9．（2023秋·吉林·七年级统考期末）如图，平面上有五个点A，B，C，D，E．按下列要求画出图形．
（1）连接BD；
（2）画直线AC交线段BD于点M；
（3）请在直线AC上确定一点N，使B，E两点到点N的距离之和最小．
【答案】（1）见解析；（2）见解析；（3）见解析
【分析】（1）根据题意连接BD即可；
（2）根据题意画直线AB交BD于点M；
（3）根据两点直线线段最短，连接BE交AC于点N，点N即为所求．
【详解】解：（1）如图，连接BD；
（2）如图，画直线AB交BD于点M；
（3）如图，连接BE交AC于点N，根据两点之间线段最短可得点N即为所求．
【点睛】本题考查了画线段，画直线，两点之间线段最短，掌握基本作图，理解线段和直线的区别是解题的关键．
10．（2022秋·内蒙古呼伦贝尔·九年级统考期末）如图，△ABC三个顶点的坐标分别为A(1，1)，B(4，2)，C(3，4)．
（1）请画出ΔABC关于原点对称的ΔA1B1C1；
（2）在x轴上求作一点P，使ΔPAB的周长最小，请画出ΔPAB，并直接写出P的坐标．
【答案】（1）答案见解析；（2）作图见解析，P坐标为(2，0)
【分析】（1）根据网格结构找出点A、B、C关于原点的对称点A1、B1、C1的位置，然后顺次连接即可；
（2）找出点A关于x轴的对称点A'，连接A'B与x轴相交于一点，根据轴对称确定最短路线问题，交点即为所求的点P的位置，然后连接AP、BP并根据图象写出点P的坐标即可．
【详解】解：（1）△A1B1C1如图所示；
（2）作点A(1，1)关于x轴的对应点A'1,−1，连接A'B交x轴于点P，则点P为所求的点，连接△APB，则△APB为所求的三角形．
此时点P坐标为(2，0)
【点睛】本题考查了利用旋转变换作图，利用平移变换作图，轴对称确定最短路线问题，熟练掌握网格结构准确找出对应点的位置是解题的关键．
11．（2022秋·北京·八年级北京市第一六六中学校考期中）在直角坐标系中，△ABC的三个顶点的位置如图所示．
(1)请画出△ABC关于y轴对称的△A'B'C'（其中A'，B'，C'分别是A，B，C的对应点，不写画法）；
(2)直接写出A'，B'，C'三点的坐标：A'（ ），B'（ ），C'（ ）
(3)在x轴上找出点P，使得点P到点A、点B的距离之和最短（保留作图痕迹）
(4)点Q在坐标轴上，且满足△BCQ是等腰三角形，则所有符合条件的Q点有__________个．
【答案】(1)见解析；
(2)4，1；2，3；−1，−2；
(3)见解析；
(4)10．
【分析】（1）由点的对称性，作出图形即可；
（2）关于y轴对称的点的坐标特点：横坐标变为相反数，纵坐标不变，即可求解；
（3）作A点关于x轴的对称点A″，连接A″B交x轴于点P，P点即为所求；
（4）利用两圆一线确定等腰三角形，作出图形即可求解．
【详解】（1）如图1：
（2）由图可知A（−4，1），B（−2，3），C（1，−2），
∴A点关于y轴对称的点为（4，1），B点关于y轴对称的点为（2，3），C点关于y轴对称的点为（−1，−2），
∴A′（4，1），B′（2，3），C′（−1，−2），
故答案为：4，1；2，3；−1，−2；
（3）如图2：作A点关于x轴的对称点A″，连接A″B交x轴于点P，
∴AP+BP=A″P+BP=A″B，
此时PA＋PB值最小；
（4）如图：以B为圆心，BC长为半径做圆，此圆与坐标轴有4个交点，
以C为圆心，BC长为半径做圆，此圆与坐标轴有4个交点，
作线段BC的垂直平分线，此线与坐标轴有2个交点，
∴△BCQ是等腰三角形时，Q点坐标有10个，
故答案为：10．
【点睛】本题考查轴对称作图，图形与坐标，熟练掌握轴对称的性质，垂直平分线的性质，等腰三角形的性质，两圆一线确定等腰三角形的方法是解题的关键．